[Перевод] Рисуем муравьями: процедурные изображения при помощи алгоритмов оптимизации муравьиной колонии
Почему мне захотелось рисовать муравьями
Я хотела создать произведение искусства, исследующее сложность проектирования программного обеспечения. Когда я представляю огромную кодовую базу, то думаю о её самостоятельно возникающей сложности и о её переплетённых, взаимосвязанных частях. Её общая форма, если так можно выразиться, возникает из действий множества отдельных личностей.
Я думала о том, как представить это графически, и одной из нашедших во мне отклик картинок стало изображение муравьиной колонии. Муравьи — прекрасный пример возникающей (эмерджентной) сложности. Ни один отдельный муравей не является архитектором, но вместе они строят великолепные сложные структуры.

Схема формикария. Источник: Wikimedia Commons.
Я начала с поиска информации о симуляциях колоний муравьёв. Очевидно, что литература об этом существует, и она прекрасна. Но хитрость заключалась в том, что муравейники возникают частично в зависимости от физики песка и земли, в которых они строятся — ведь из создание зависит от того, как расположится частица, когда её положит муравей. Я хотела создать что-то в 2D, поэтому стремилась сразу перейти к симуляции без написания кода физики песка, то есть мне пришлось отказаться от физической симуляции муравейника.
Из-за этого я снова принялась за поиски, и они привели меня к совершенно другому классу симуляций муравьёв: алгоритмам оптимизации муравьиной колонии (муравьиным алгоритмам).
Оптимизация муравьиной колонии — это агентный алгоритм, используемый для решения задачи нахождения кратчайшего пути между двумя точками графа. «Агентный» означает, что алгоритм состоит из отдельных процедур (в данном случае — «муравьёв»), эмерджентное поведение которых решает задачу.
Работает это очень просто. Каждый муравей оставляет на своём пути след из «феромонов». Муравьи оставляю один тип феромонов после выхода из муравейника и другой — когда найдут еду. Ищущие еду муравьи стремятся найти след «пищевого» феромона, а ищущие муравейник — след «домашнего» феромона.
Муравьи, оказавшиеся на более коротком пути, способны быстрее проделать маршрут от дома до еды и обратно. Это означает, что они создадут более насыщенный слой феромонов. Муравьи, движущиеся более долго, будут предпочитать более насыщенный след и двигаться по более короткому пути. Каждый отдельный муравей работает по очень простым правилам, но со временем муравьи находят более оптимальный путь между двумя точками.
Симуляция
Я написала свой симулятор муравьёв на Processing 3. Собственную реализацию я начала с имитирования кода из этого потрясающего поста Грегори Брауна.
После того, как муравьи начали двигаться, я приступила к расширению и модификации кода, чтобы он лучше работал в более масштабных сетках пикселей. Я хотела получить интересно выглядящие симуляции (необязательно эффективные) и это определило мою работу над кодом. Я создала для муравьёв очень рудиментарное зрение, чтобы каждый муравей мог видеть на несколько пикселей вперёд. Я добавила смерть и возрождение муравьёв, чтобы они не разбредались хаотично по всему пространству. Наконец, я сделала муравьёв немного глупее: они оставляют феромон постоянно, даже если поиск оказался неудачным, что похоже на реальное поведение муравьёв.
Здесь можно сыграть в порт симуляции на p5.js прямо в браузере!
Можете также взглянуть на портированный исходный код на Github.
Больше всего в симуляции меня восхитили красивые, странные и сложные формы, создаваемые муравьями. Они не маршируют по прямым линиям, а образуют петли, витки и ответвления. Ещё интереснее то, что вы можете управлять видом создаваемых муравьями фигур, изменяя различные переменные их мира. Например, можно изменять скорость испарения феромона и дальность зрения муравьёв в пикселях.
Превращаем муравьёв в искусство
После того, как симуляция начала работать, следующим шагом стало исследование выводимых ею данных. Моя цель заключалась в создании некоего двухмерного изображения, то есть мне нужно было захватывать и отрисовывать создаваемые муравьями фигуры.
В конечном итоге я написала разные типы вывода: несколько типов растрового вывода и один векторный. Для захвата растрового вывода я отслеживала посещённые муравьями ячейки и частоту их визитов. Поиграв с фильтрами этого вывода, можно получить призрачный след тех мест, где побывали муравьи.

Пример растрового вывода. Пути намного шире вдоль популярных следов муравьёв и там, где муравьи случайным образом бродили вокруг муравейника.
Растровый вывод был интересным, но я хотела, чтобы были чётче видны отдельные пути, поэтому исследовала возможность экспорта в svg. Для векторного вывода я сохраняла историю каждого муравья, и когда они достигали пищи или муравейника, записывала эту историю в список. Для рендеринга я сэмплировала каждый сохранённый путь и отрисовывала его как серию кривых.

Пример векторного вывода. Здесь можно увидеть отдельные пути муравьёв. Там, где прошло много муравьёв, немного накладывающиеся друг на друга линии образую более широкие пути.
Соединяем точки
Я знала, что хотела отрисовать муравьёв, путешествующих между множеством точек, поэтому одним из первых стал код для компоновки нескольких симуляций в одно изображение. Но что же тогда мне рисовать?
Сначала я решила создать очень буквальные графы: начав с простых двоичных деревьев, перейти потом к более сложным визуализациям. Это казалось естественным шагом, ведь оптимизация муравьиной колонии решает задачи поиска путей в графах. Ещё я подумала, что это будет интересным способом визуализации сложности кода: почему бы не взять UML-диаграмму или граф зависимостей и не отрендерить их при помощи муравьёв?
Я уже была знакома с Graphviz, поэтому решила использовать этот набор инструментов и язык описания графов DOT для задания узлов и рёбер моей симуляции. Graphviz имеет режим, выводящий файл DOT с аннотациями координат пикселей. Я написала очень уродливый парсер файлов DOT и использовала его с аннотированным файлом DOT для симулирования местоположений муравейников и пищи.
Эксперименты с двоичными деревьями показались многообещающими и придавали очень естественный, органический внешний вид.

Простое двоичное дерево. Мне сказали, что оно походит на ангиограмму.

Немного более сложное дерево, уже довольно глубокое.
Затем я начала строить графы побольше, используя в качестве входных данных различные кодовые базы. Я написала несколько простых скриптов на Python: один превращал git-дерево в файл DOT, другой превращал зависимости импорта C в файл DOT.

Граф объектов в дереве объектов git, нарисованный муравьями.

Зависимости между файлами в ядре Linux. Узлы и рёбра были созданы при помощи квадратного стиля графов Graphviz. На самом деле, ненамного интереснее случайных графов.
Хотя все эти графы интересны и определённо сложны, меня разочаровало то, что на самом деле они ничего не говорили об общей форме кодовых баз, на основе которых были построены. Чем больше я экспериментировала с визуализацией кода, тем больше осознавала, что построение интересного графа из кодовой базы само по себе является отдельной, более сложной задачей. Однако мне понравилась сложность очень больших графов и позже я к этому снова вернулась.
Моим следующим экспериментом стали игры с простыми формами. Я создавала графики из линий, окружностей, синусоид и других фигур, которые легко описать при помощи узлов и рёбер.

Точки на отрезке, в правой части отрезка точки расположены ближе друг к другу.
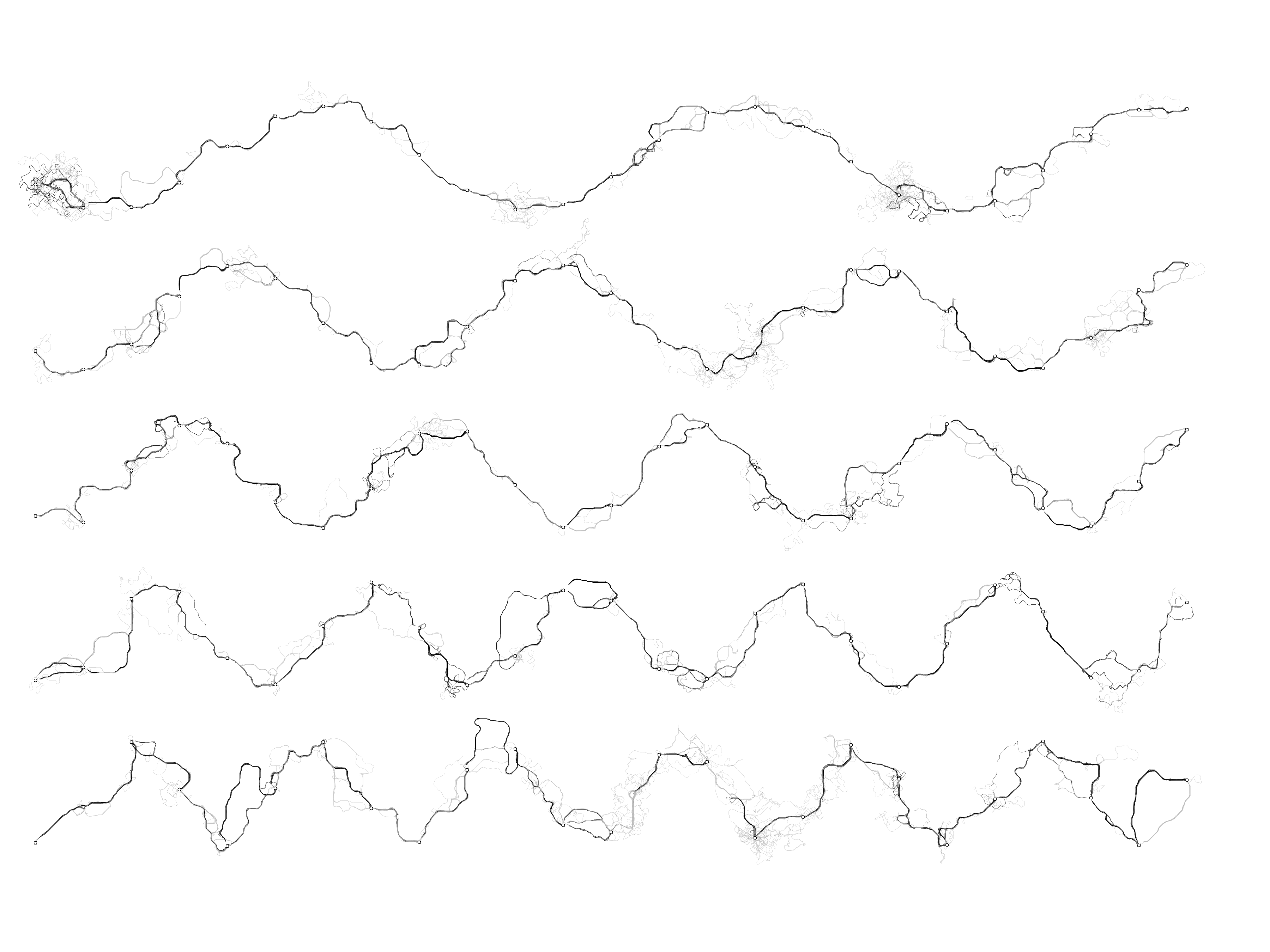
Различные частоты синусоиды. Полагаю, из муравьёв выйдет вполне неплохой осциллограф.
Наиболее интересными мне показались простые триангулированные пространства. Я сгенерировала множество равномерно распределённых точек — или случайным образом, или рисованием фигур —, а затем использовала библиотеку Processing, чтобы превратить эти точки в триангуляцию Делоне или диаграмму Вороного. Затем получившиеся рёбра были использованы для симуляции муравьёв, где каждое ребро обозначало один «муравейник» или «пищу».

Нарисованная муравьями диаграмма Вороного.
Это привело к появлению красивого полного пространства сложных муравьиных хитросплетений, которое гораздо лучше описывало интересующую меня сложность.
Наконец, я подошла к задаче под ещё одним углом. Один друг взглянул на симуляцию и спросил, что случится, когда муравьи столкнутся со стеной — смогут ли они обходить простые препятствия? Мой код уже умел обрабатывать стены как пограничные случаи, поэтому я просто добавила внутренние стены, а потом потратила много времени, пытаясь научить муравьёв решать лабиринты.

Пути муравьёв, пытающихся решить простой лабиринт. Вы можете увидеть форму лабиринта, заметив, куда муравьи не могут пройти.
У меня была задумка, что если муравьи могут решать простые лабиринты, то можно объединить их вместе, чтобы создать более масштабную работу. Я потратила много времени на настройку переменных симуляции, чтобы муравьи могли решать их, но мне так и не удалось заставить их решать лабиринты стабильно. В конечном итоге всё это превратилось просто в завитки муравьиных путей, ограниченные формой самого лабиринта.
Готовое произведение искусства
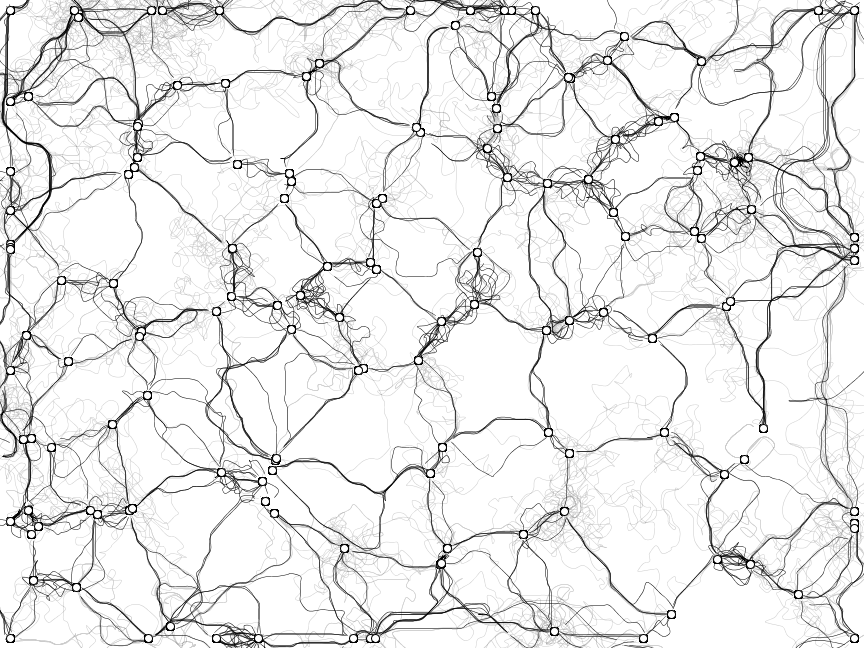
На этом этапе я решила сделать шаг назад и рассмотреть выходные данные всех своих экспериментов. Я поняла, что самые интересные изображения получались из больших полей полуслучайных точек и рёбер, и решила сделать это своим окончательным решением, настроив симуляцию на отрисовку линий между триангуляцией Делоне случайных точек.

Завершённый прогон симуляции. Он содержит множество наложенных друг на друга путей, из которых получаются нечёткие пятна.
Последняя проблема заключалась в том, как превратить изгибы SVG в готовую работу. Из экспериментов я знала, что хочу каким-то образом сортировать пути, чтобы выделить пути с красивой формой. Но прогон готовой симуляции занимал один-два часа, из-за чего изменять переменные при каждом прогоне эксперимента было неудобно.
Я решила написат вторую диаграмму Processing, которая будет загружать вывод симуляции в SVG, а затем применять нужные мне визуальные эффекты. Более того, я хотела сделать скрипт постобработки интерактивным, чтобы можно было экспериментировать с разными весами и цветами линий, а также порогами сортировки.
Я попробовала несколько разных способов оценки путей, которые должны быть на переднем и на заднем плане. Были вычислены несколько различных факторов: количество самопересечений линии, количество пересечений линией её линии уклона и вероятность того, что линия будет следовать по уклону, предсказанному предыдущими двумя точками.
Я использовала скрипт постобработки для экспериментов с разными весами и значениями этих оценок, пока не добилась нужного мне внешнего вида.

Настройка порога для передних и фоновых линий.
На этом этапе очень помогло сохранение изображения при изменении каждой переменной. Когда я приближалась к нужному мне изображению, было намного проще сравнивать ряд незначительных вариаций, чем менять несколько факторов за раз.
После длительной настройки и внесения небольших изменений я создала из своей симуляции такое изображение:

Я приблизила область, которая показалась мне наиболее интересной, и откадрировала её для создания хорошего баланса между пустым и заполненным пространством.
Последним этапом был выбор способа превращения этого изображения в физический объект. Раньше я печатала их цифровым образом как постер размером 40×50 см и предприняла попытку (неудачную) печати экрана на цветной бумаге. Постер с цифровой печатью выглядит отлично, но в дальнейшем я хочу скопировать изображение как часть картины. Я нахожу сложные рисунки медитативными и думаю, что смогу добиться интересных эффектов, отрисовывая их вручную.
На этот проект было потрачено намного больше времени, чем я ожидала, и он оказался сложнее, чем представлялось в начале. Но это отличный способ экспериментирования со всевозможной вычислительной геометрией и алгоритмическими задачами. Думаю, довольно иронично, что я написала несколько тысяч строк кода для работы, посвящённой сложности, но довольна тем, что она выглядит круто и говорит сама за себя.
