[Из песочницы] Теория графов в машинном обучении для самых маленьких06.02.2020 00:47

Сложность представления данных для глубокого обучения растет с каждым днем. Нейронные сети на основе данных в виде графа (Graph Neural Network, GNN) стали одним из прорывов последних лет. Но почему именно графы набирают все большую популярность в машинном обучении?

Конечной целью моего повествования является общее представление графов в приемах машинного обучения. Статья не претендует на научную работу, которая в полной мере описывает всю мощь представления графов, а лишь знакомит читателя с этим удивительным и сложным миром. Публикация отлично подойдет, как для закаленных в боях профессионалов, которые еще не знакомы с представлением графов в глубоком обучении, так и для новичков в этой сфере.

Автоматическое выделение важных признаков, необходимых для решения задачи — одна из главных причин успешного применения машинного обучения. Но традиционно при работе с графами, подходы машинного обучения полагались на определяемую пользователем эвристику, чтобы извлечь особенности кодирования структурной информации о графе. Тем не менее, тенденция последних лет сменилась: все чаще стали появляться подходы, в которых автоматически учатся кодировать структуру графа в низкоразмерные вложения с использованием методов глубокого обучения и нелинейного уменьшения размерности.

В машинном обучении на графах можно выделить две центральные проблемы: включение информации о структуре графа в модель (т.е. простой способ кодирования этой информации в вектор признаков) и уменьшение размерности вектора признаков.

Для извлечения структурной информации из графов традиционные машинные подходы часто основаны на сводной статистике графов (например коэффициентах кластеризации), функциях ядра или тщательно разработанных функциях для измерения локальных структур окрестности. Однако эти подходы ограничены, потому что эти инженерные решения не могут адаптироваться в процессе обучения, а их разработка является трудоемким и дорогостоящим процессом.

Говоря о графах, как о структурных единицах представления данных, можно задать себе простой вопрос: почему именно графы?

Графы — один из самых мощных и гибких способов представления данных. Они обладают большой выразительной силой, то есть графы могут использоваться как обозначение большого числа систем в различных областях, включая общественные науки (социальные сети) [1], [2], естествознание (физические системы [3], [4] и сети межбелкового взаимодействия [5]), графы знаний [6] и многие другие области исследований [7].

В большинстве CV/ML систем данные могут рассматриваться как графы, несмотря на то, что мы привыкли использовать их представления в качестве других структур данных. Отображение данных в виде графов дает большую гибкость и может дать совершенно другой, интересный, взгляд на различные проблемы [8].

Проще говоря, с помощью графа мы можем представить сколь угодно сложные данные. Такая структура подходит начиная от разработки лекарств и заканчивая рекомендациями по дружбе в социальных сетях. Как следствие их повсеместности в нашей жизни, мы видим, что графы стали являться основой многочисленных систем, позволяющих эффективно хранить и получать доступ к реляционным знаниям о взаимодействующих объектах.

В последнее время наблюдается всплеск подходов, которые стремятся изучить представления (embeddings), которые кодируют структурную информацию о графике. Идея, лежащая в основе этих подходов к обучению представления, состоит в том, чтобы изучить отображение, которое представляет узлы или целые (под)графы, как точки в низкоразмерном векторном пространстве $R^d$ . Цель состоит в том, чтобы оптимизировать это отображение так, чтобы геометрические отношения в этом изученном пространстве отображали структуру исходного графа. После оптимизации пространства отображения, изученные представления могут быть использованы в качестве входных данных для последующих задач машинного обучения.

Ранее проблема сбора структурной информации о графе рассматривалась как шаг предварительной обработки, использующий вручную спроектированную статистику для извлечения структурной информации. Сейчас, напротив, подходы обучения представлений рассматривают эту проблему как саму задачу машинного обучения. Алгоритмы, основанные на данных, создают представления, которые кодируют структуру графа.

Большинство современных алгоритмов представления узлов опираются на то, что мы называем прямым кодированием (direct encoding), когда топологическая информация хранится в явном виде. Эти подходы во многом основаны на классических методах факторизации матрицы для уменьшения размерности и многомерного масштабирования. Действительно, многие из этих подходов изначально были мотивированы как алгоритмы факторизации, а затем были переосмыслены в рамках концепции кодер-декодер. Различают подходы, основанные на матричной факторизации, и более современные подходы, основанные на случайных прогулках.

Одни из хорошо известных алгоритмов DeepWalk и node2vec тоже полагаются на прямое кодирование с использованием своего собственного декодера. В качестве меры оптимизации у них выступает алгоритм, который оптимизирует представление для кодирования статистики случайных прогулок. Благодаря использованию современных подходов, эти алгоритмы считаются наиболее релевантными среди общедоступных решений.

Последние разработки в сфере методов представления узлов способны решить ряд важных проблем (о которых мы говорим чуть позже). Это стало возможным благодаря использованию автоэнкодера окрестностей (DNGR и SDNE), агрегации окрестностей, механизмов внимания и некоторых других продвинутых алгоритмов [9].

Обозначения и основные предположения

Графом является пара $G = (V, E)$ , где $V$ представляет собой набор, элементы которого называются вершинами, а $E$ — это набор из двух множеств (наборов с двумя различными элементами) вершин, элементы которых называются ребрами.

Рассмотрим простейший неориентированный граф (рис. 1). Для такого графа имеем: $V = \\{1,2,3,4,5,6\\}$ и $E = \\{\\{1, 2\\},\\{1, 5\\},\\{2, 3\\},\\{2, 5\\},\\{3, 4\\},\\{4, 5\\},\\{4, 6\\}\\}$

Несмотря на то, что многие графы реального мира имеют сложную мультимодальную или многослойную структуру, мы для простоты сосредоточимся на простых, неориентированных графах (стоит отметить, что ряд современных алгоритмов представляют возможность справляться с неоднородной топологией графов). Подробнее про теорию графов можно почитать тут.

Предположим, что основным входным сигналом для нашего алгоритма обучения представлений является неориентированный граф $G = (V, E)$ со связанной двоичной матрицей смежности $A$ . Мы также предполагаем, что методы могут использовать вещественную матрицу атрибутов узла $X ∈ R^{m*|V|}$ (например представление текста или метаданных, связанных с узлами). Цель состоит в том, чтобы использовать информацию, содержащуюся в $A$ и $X$ , чтобы отобразить каждый узел или подграф на вектор $z ∈ R^d$ , где $d << |V|$ .

Большинство используемых методов оптимизируют это отображение без учителя, используя только информацию в $A$ и $X$ , не зная последующей задачи машинного обучения. Тем не менее, существуют некоторые подходы к обучению репрезентативного представления, где модели используют классификационные или регрессионные метки для оптимизации представлений. Эти классификационные метки могут быть связаны с отдельными узлами или целыми подграфами и являются целями прогнозирования для последующих задач машинного обучения (например, они могут обозначать роли белка или терапевтические свойства молекулы на основе ее графического представления)

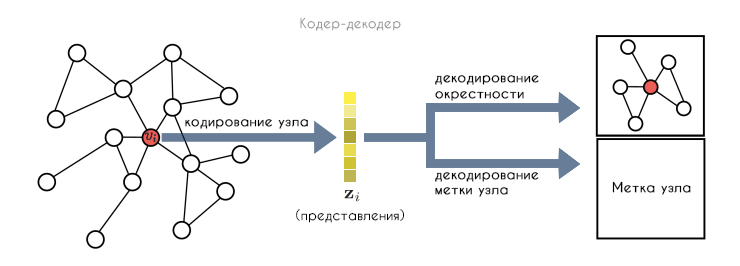
Подход кодер-декодер заключается в том, что сначала кодер отображает узел $v_i$ в низкоразмерное векторное вложение $z_i$ на основе положения узла в графе, его структуры локальных окрестностей и/или его атрибутов. Затем декодер извлекает указанную пользователем информацию из низкоразмерного внедрения; это может быть информация о локальной окрестности графа $v_i$ (например идентификация его соседей) или метка классификации, связанная с $v_i$ (например метка сообщества). Совместно оптимизируя кодер и декодер, система учится сжимать информацию о структуре графа в низкоразмерное пространство представлений.

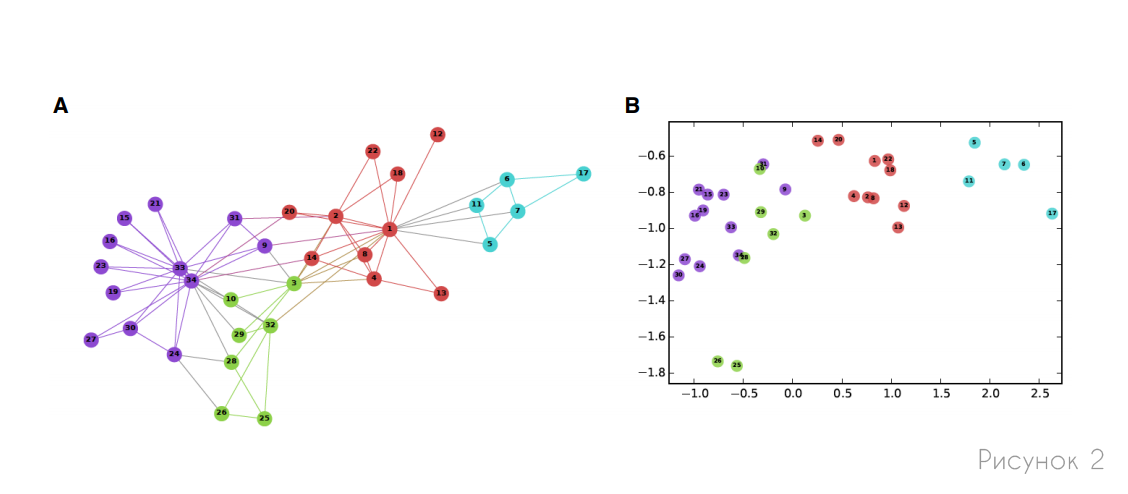
Мы начнем с обсуждения методов представления узлов, где цель состоит в том, чтобы закодировать узлы как низкоразмерные векторы, которые суммируют их положение в графе и структуру локальной окрестности графа. Эти низкоразмерные вложения можно рассматривать как кодирование или проецирование узлов в скрытое пространство, где геометрические отношения в этом пространстве соответствуют взаимодействиям (например, ребрам) в исходном графе. На рисунке 2 представлен пример представления социальной сети, где вложения двумерных узлов отражают структуру сообщества, неявную в сети.

Можно сказать, что кодировщик — это функция, которая отображает узлы на векторные представления, $z_i ∈ R^d$ (где $z_i$ соответствует представлению для узла $v_i ∈ V$ ):

$\textbf{ENC: } V → R^d$

Тогда декодер — функция, которая принимает набор представлений узлов и декодирует пользовательскую графовую статистику из этих вложений:

$\textbf{DEC: } R^d * R^d → R^+$

Из обширного числа декодеров чаще всего предпочтение отдается попарному декодеру. Эта разновидность декодеров, которая отображает пары представлений узлов в реальную меру близости графа, которая количественно определяет близость двух узлов в исходном графе. Это значит, что когда мы применяем попарный декодер к паре представлений $(z_i, z_j)$ , мы получаем реконструкцию близости между $v_i$ и $v_j$ в исходном графе. В такой структуре целью является оптимизация отображений кодера и декодера для минимизации ошибки или потери так, чтобы:

$DEC(ENC(v_i), ENC(v_j)) = DEC(z_i, z_j ) ≈ sG(v_i, v_j) \textbf{ (1)}$

Где $sG$ — это определяемая пользователем мера близости между узлами, определенная над графом $G$ . Например, можно установить $sG(z_i, z_i) ≜ A_i,_j$ и определить узлы так, чтобы смежные ноды были близки к 1, а разрозненные к 0. Или можно определить $sG$ в соответствии с вероятностью одновременного появления $v_i$ и $v_j$ при случайной прогулке с фиксированной длиной по графику $G$ . На практике большинство подходов реализуют восстановление (уравнение 1) путем минимизации эмпирических потерь $L$ по набору пар обучающих узлов $D$ :

$L = \sum_{(v_i, v_j) ∈ D} ℓ (DEC(z_i, z_j), sG(v_i, v_j))$

Где $ℓ = R * R → R$ — заданная пользователем функция потерь, которая измеряет расхождение между декодированными (т.е. предполагаемыми) значениями близости $DEC(z_i, z_j)$ и истинными значениями $sG(v_i, v_j)$ .

После того, как мы оптимизировали систему кодер-декодер, мы можем использовать обученный кодер для генерации представлений для узлов, которые затем можно использовать в качестве входных данных для задач машинного обучения в нисходящем направлении. Например, можно передать полученные вложения в классификатор логистической регрессии, чтобы предсказать сообщество, которому принадлежит узел, или можно использовать расстояния между представлениями, чтобы рекомендовать дружеские ссылки в социальной сети.

Такой подход сильно напоминает seq2seq сети, где входная последовательность слов кодируется в низкоразмерное представление, а затем декодируется для различных предсказаний. Все приемы, которые можно применить для сетей seq2seq, могут быть реализованы и для GNN [10].

Основные методологические различия между различными подходами представления узлов состоят в том, как они определяют четыре компонента:

Функция парной близости : , определенная над графом .
Функция кодировщика ENC, которая генерирует представления узлов. Эта функция содержит ряд обучаемых параметров, которые оптимизируются на этапе обучения.
Функция декодера DEC, которая восстанавливает значения попарной близости из сгенерированных представлений. Эта функция обычно не содержит обучаемых параметров
Функция потерь , которая определяет, как оценивается качество парных реконструкций для обучения модели.

Вот сводка некоторых известных алгоритмов прямого кодирования. Обратите внимание, что декодер и функция приближения для методов на основе случайной прогулки асимметричны. Причем функции приближения соответствует вероятность посещения при случайной прогулке фиксированной длины, начиная с .

Многие успешные из современных методов, которые также принадлежат к классу подходов прямого кодирования, изучают представления узлов на основе статистики случайного обхода. Их ключевым нововведением является оптимизация, при которой узлы имеют похожие представления, если они имеют тенденцию сосуществовать при коротких случайных обходах по графику (рис. 3). Таким образом, вместо использования детерминированной меры близости к графу, в этих методах случайной прогулки используется гибкая стохастическая мера близости к графу, которая привела к превосходной производительности в ряде параметров.

Подходы DeepWalk и node2vec, в отличие от других подходов матричной факторизации, которые тоже полагаются на прямое кодирование, используют свой собственный декодер. К тому же вместо того, чтобы пытаться декодировать фиксированную детерминистическую меру расстояния, они оптимизируют представления для кодирования статистики случайных прогулок. Основная идея этих подходов состоит в том, чтобы изучить представления так, чтобы:

$DEC(z\_i, z\_j) ≜ \dfrac{e^{z\_i^Tz\_j}}{\sum_{v_k∈V}e^{z_i^Tz_k}} ≈ pG,T(v\_j|v\_i) \textbf{ (2)}$

Где $pG,T (v_j|v_i)$ — вероятность посещения $v_j$ в случайной прогулке по длине $T$ , начиная с $v_i$ , причем $T$ обычно определено в диапазоне $T ∈ \\{2, ..., 10\\}$ . Обратите внимание, что $pG,T (v_j|v_i)$ является стохастическим и асимметричным. Более формально, эти подходы пытаются минимизировать следующую потерю перекрестной энтропии:

$ℓ=\sum_{(v_i,v_j)∈D}−log(DEC(z_i, z_j)) \textbf{ (3)}$

В этом случае обучающий набор $D$ генерируется путем выборки случайных прогулок, начиная с каждого узла (т.е. где $N$ пар для каждого узла $v_i$ выбираются из распределения $(v_i, v_j) \sim pG,T(v_j|v_j)$ . Однако наивная оценка этой потери непомерно дорога — $O(|D||V|)$ (поскольку оценка знаменателя уравнения (2) имеет временную сложность $O(|V|)$ ). Таким образом, DeepWalk и node2vec используют разные оптимизации и приближения для вычисления потерь в уравнении (3). DeepWalk использует метод иерархического softmax для вычисления нормализующего фактора, используя структуру двоичного дерева для ускорения вычислений. Напротив, node2vec аппроксимирует уравнение (3), используя отрицательную выборку: вместо нормализации по всему набору вершин, алгоритм аппроксимирует нормирующий коэффициент, используя набор случайных «отрицательных выборок».

Помимо этих алгоритмических различий, ключевое различие между node2vec и DeepWalk заключается в том, что первый позволяет гибко определять случайные обходы, тогда как второй использует простые непредвзятые случайные обходы по графу. В частности, node2vec вводит два гиперпараметра случайных прогулок: $p$ и $q$ , которые позволяют контролировать смещение во время прогулок (рис. 4). Гиперпараметр $p$ контролирует вероятность возврата к предыдущему узлу, в то время как $q$ управляет вероятностью исследовать неизученные части графа. Вводя эти гиперпараметры, node2vec может плавно интерполировать между обходами, которые больше похожи на поиск в ширину или в глубину.

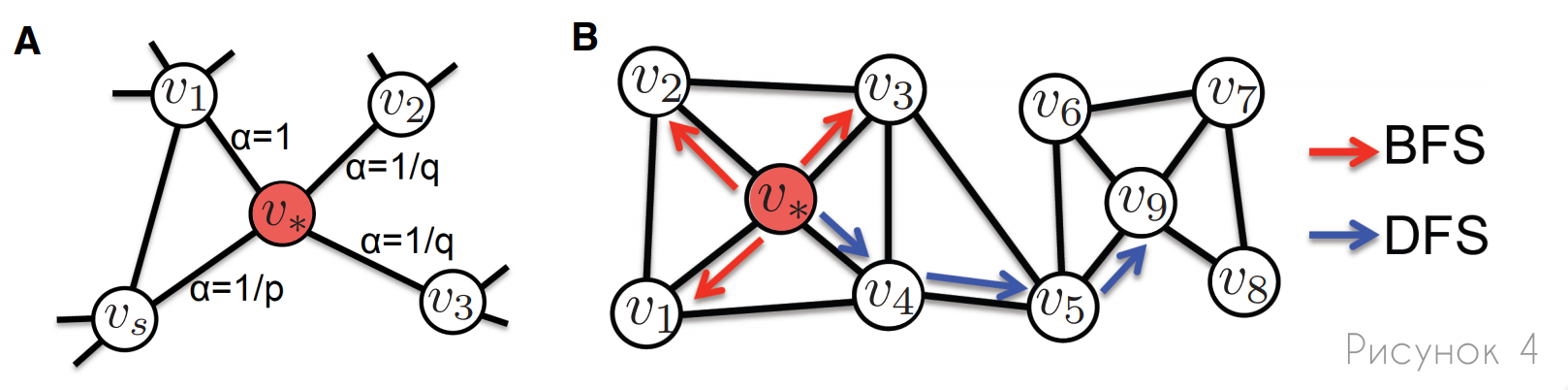
A: Иллюстрация того, как node2vec смещает прогулки, используя параметры p и q. Предполагая, что прогулка только что перешла от $v\_s$ к $v\_∗$ , метки ребер (α) пропорциональны вероятности того, что прогулка выберет именно это ребро на следующем шаге.

B: Разница между случайными прогулками, основанными на поиске по ширине (BFS) и поиске по глубине (DFS). Случайные прогулки, подобные BFS, в основном ограничиваются изучением непосредственных соседей узла и, как правило, более эффективны для захвата неких структурных ролей. Тогда как, прогулки, основанные на DFS, изучают более отдаленные узлы и применяются для захвата структур сообщества в целом.

До сих пор все рассмотренные нами методы представления узлов были основаны на том, что кодер представляет собой простой поиск представлений. Однако эти подходы прямого кодирования обучают уникальные векторы представлений независимо для каждого узла, что приводит к ряду недостатков:

Ни один параметр не распределен между узлами в кодере (т.е. кодер является просто поиском представлений на основе произвольных идентификаторов узлов). Это неэффективно, как статистически, так и вычислительно.
Прямое кодирование также не позволяет использовать атрибуты узла во время кодирования. Во многих больших графах узлы имеют атрибутивную информацию (например, профили пользователей в социальной сети), которая часто очень информативна в отношении положения и роли узла в графе.
Методы прямого кодирования по своей природе являются трансдуктивными. Это значит, что они могут генерировать представления только для узлов, которые присутствовали на этапе обучения (если не выполняются дополнительные улучшающие раунды, чтобы оптимизировать представления для новых узлов). Это очень проблематично для развивающихся, массивных графов, которые не могут быть полностью сохранены в памяти, или областей, которые требуют обобщения для новых графов после обучения.

Недавно был предложен ряд подходов для решения некоторых/всех этих проблем. Эти подходы все еще прочно входят в рамки концепции кодер-декодер, но они отличаются от прямых методов кодирования в том, что они используют более сложные кодеры, которые в целом зависят от структуры и атрибутики графа.

Отображения в виде глубокого нейронного графа (DNGR) и структурная глубокая сеть представлений (SDNE) решают одну из проблем, описанных выше: в отличие от методов прямого кодирования, они напрямую включают структуру графа в алгоритм кодера. Основная идея этих подходов состоит в том, что они используют автоэнкодеры — хорошо известный подход глубокого обучения, для сжатия информации о локальной окрестности узла (рис. 5). DNGR и SDNE также отличаются от ранее рассмотренных подходов тем, что они используют унарный декодер вместо попарного.

В этих подходах каждый узел $v_i$ связан с вектором окрестности $s_i ∈ R^{|V|}$ , который соответствует строке $v_i$ в матрице $S$ (где $S$ отображает близость парных узлов — $S_i,_j = sG (v_i , v_j)$ ). Вектор $s_i$ содержит парную близость графа $v_i$ ко всем остальным узлам и функционирует как многомерное векторное представление окрестности $v_i$ . Цель автоэнкодера для DNGR и SDNE состоит в том, чтобы представлять узлы с использованием $s_i$ векторов таким образом, что потом векторы $s_i$ можно было бы восстановить из этих представлений:

$DEC(ENC(s_i)) = DEC(z_i) ≈ s_i$

Другими словами, потеря для этих методов принимает следующую форму:

$ℓ=\sum_{v_i∈V} ||DEC(z_i) − s_i||^2_2$

Как и в случае попарного декодера, размерность представлений $z_i$ намного меньше, чем $|V|$ (размерность векторов), поэтому цель состоит в том, чтобы сжать информацию о соседях узла в низкоразмерный вектор. Как для SDNE, так и для DNGR, функции кодера и декодера состоят из нескольких сложенных слоев нейронной сети: каждый уровень кодера уменьшает размерность его входа, а каждый уровень декодера увеличивает размерность его входа (рис. 5).

SDNE и DNGR отличаются функцией подобия, которые используются для построения векторов окрестности $s_i$ , а также в деталях того, как оптимизируется автоэнкодер. DNGR определяет $s_i$ в соответствии с точечной взаимной информацией двух узлов, совместно встречающихся при случайных прогулках, аналогично DeepWalk и node2vec. SDNE просто устанавливает $s_i ≜ Ai$ , то есть равным вектору смежности $v_i$ .

Несмотря на то, что методы SDNE и DNGR позволяют включать структурную информацию о локальной окрестности узла непосредственно в кодировщик в виде регуляризации, что невозможно для подходов прямого кодирования (поскольку их кодировщик зависит только от идентификатора узла), они по-прежнему остаются подвержены трансдуктивности. К тому же входное измерение для автоэнкодера зафиксировано на $|V|$ , что может быть чрезвычайно дорогостоящим и даже неразрешимым для графов с миллионами узлов.

Стоит отметить, что на данный момент в сфере алгоритмов графов не существует панацеи. Любой метод в той или иной степени подвержен серьезным ограничениям. Оставшиеся алгоритмы, такие как агрегация окрестностей, сверточные кодеры, механизмы внимания и многие другие [9], пытаются решить обозначенные вопросы. К сожалению, рассмотрение этих методов сильно выходит за рамки ознакомительного курса и будет раскрыто в отдельной статье.

Подходы к репрезентативному обучению для машинного обучения на графах предлагают мощную альтернативу традиционному проектированию объектов. Однако предстоит еще проделать большую работу, как в плане повышения эффективности этих методов, так и, возможно, что еще более важно, в разработке последовательных теоретических основ, на которых могут основываться будущие инновации.

В дополнение к общим задачам, изложенным выше, существует ряд конкретных открытых проблем, которые еще предстоит решить в области обучения представлений на графах.

Масштабируемость. Хотя большинство современных работ теоретически хорошо масштабируются (т.е время обучения $O(|E|)$ ), еще предстоит проделать значительную работу в подходах масштабирования узлов и графиков к действительно массивным наборам данных (например миллиардам узлов). Большинство методов основаны на обучении и хранении уникальных вложений для каждого отдельного узла. Более того, большинство установок оценки предполагают, что атрибуты, представления и списки ребер всех узлов, используемых как для обучения, так и для тестирования, могут уместиться в основной памяти — предположение, которое противоречит реальности большинства областей применения, где графы являются массивными, развивающимися и часто хранится в распределенном виде. Разработка рамок обучения репрезентации, которые действительно масштабируются до реальных производственных параметров, необходима, чтобы предотвратить расширение разрыва между сообществом академических исследований и реальными потребителями этих подходов.

Использование структур высшего порядка. Хотя в последние годы большая работа была посвящена уточнению и совершенствованию алгоритма кодирования, используемого для генерации представлений узлов, большинство методов по-прежнему полагаются на базовые попарные декодеры, которые прогнозируют парные отношения между узлами и игнорируют структуры графа более высокого порядка, включающие более двух узлов. Хорошо известно, что структурные мотивы высшего порядка имеют важное значение для структуры и функционирования сложных сетей, а разработка алгоритмов декодирования, способных декодировать такие сложные конфигурации, является важным направлением будущей работы.

Моделирование динамических графов. Многие области применения включают в себя высокодинамичные графы, где информация о синхронизации имеет решающее значение, например, сети обмена мгновенными сообщениями или графы финансовых транзакций. Однако нам не хватает подходов представлений, которые могут справиться с уникальными проблемами, представленными динамическими графами, такими как задача включения временной информации о ребрах. Временные графы становятся все более важным объектом исследования, и расширение методов представления графов для работы над ними откроет широкий спектр интересных прикладных областей.

Улучшение интерпретируемости. Обучение представлений является привлекательной областью, потому что оно освобождает большую часть бремени ручных функций проектирования, но оно также имеет общеизвестную стоимость интерпретируемости. Мы знаем, что подходы на основе представлений обеспечивают современную производительность, но фундаментальные имитации и возможные основные отклонения этих алгоритмов до конца не изучены. Чтобы двигаться вперед, необходимо позаботиться о разработке новых методов, улучшающих интерпретируемость изученных представлений, помимо визуализации и оценки производительности. Учитывая сложности и репрезентативные возможности этих подходов, исследователи должны всегда проявлять бдительность, чтобы гарантировать, что их методы действительно учатся представлять соответствующую информацию графа, а не обобщают статистические тенденции.

В заключении мне бы хотелось сказать, что сейчас теория графов — одно из наиболее перспективных направлений в машинном обучении. Обуздав всю мощь, которую могут дать представления графов, человечество сделает огромный шаг на пути к созданию первого прототипа искусственного интеллекта.

[1] — W.L. Hamilton, Z. Ying, and J. Leskovec, «Inductive representation learning on large graphs,» NIPS 2017, pp. 1024–1034, 2017.
[2] — T.N. Kipf and M. Welling, «Semi-supervised classification with graph convolutional networks,» ICLR 2017, 2017.
[3] — A. Sanchez-Gonzalez, N. Heess, J.T. Springenberg, J. Merel, M. Riedmiller, R. Hadsell, and P. Battaglia, «Graph networks as learnable physics engines for inference and control,» arXiv
preprint arXiv:1806.01242, 2018.
[4] — P. Battaglia, R. Pascanu, M. Lai, D.J. Rezende et al., «Interaction networks for learning about objects, relations and physics,» in NIPS 2016, 2016, pp. 4502–4510.
[5] — A. Fout, J. Byrd, B. Shariat, and A. Ben-Hur, «Protein interface prediction using graph convolutional networks,» in NIPS 2017, 2017, pp. 6530–6539.
[6] — T. Hamaguchi, H. Oiwa, M. Shimbo, and Y. Matsumoto, «Knowledge transfer for out-of-knowledge-base entities: A graph neural network approach,» in IJCAI 2017, 2017, pp. 1802–1808.
[7] — H. Dai, E.B. Khalil, Y. Zhang, B. Dilkina, and L. Song, «Learning combinatorial optimization algorithms over graphs,» arXiv preprint arXiv:1704.01665, 2017.
[8] — X. Liang, X. Shen, J. Feng, F. Lin, S. Yan, «Semantic Object Parsing with Graph LSTM», arXiv:1603.07063v1 [cs.CV] 23 Mar 2016.
[9] — Z. Wu, S. Pan, F. Chen, G. Long, C. Zhang, Philip S. Yu, «A Comprehensive Survey on Graph Neural Networks», arXiv:1901.00596v4 [cs.LG] 4 Dec 2019.
[10] — P. Veličković, G. Cucurull, A. Casanova, A. Romero, P. Liò, Y. Bengio, «Graph Attention Networks», arXiv:1710.10903v3 [stat.ML] 4 Feb 2018.

Graph Neural Networks: A Review of Methods and Applications
Representation Learning on Graphs: Methods and Applications