Полосный вокодер на Python: поговорим как роботы22.12.2022 16:32

Если честно, сейчас сложно придумать практическое применение для полосного вокодера. Скорее всего, он придется вам по душе, если вы большой любитель ретро-технологий, или — что не исключено — вы начинающая FKA Twigs или Daft Punk и любите играть с футуристичными звуками в своей музыке.

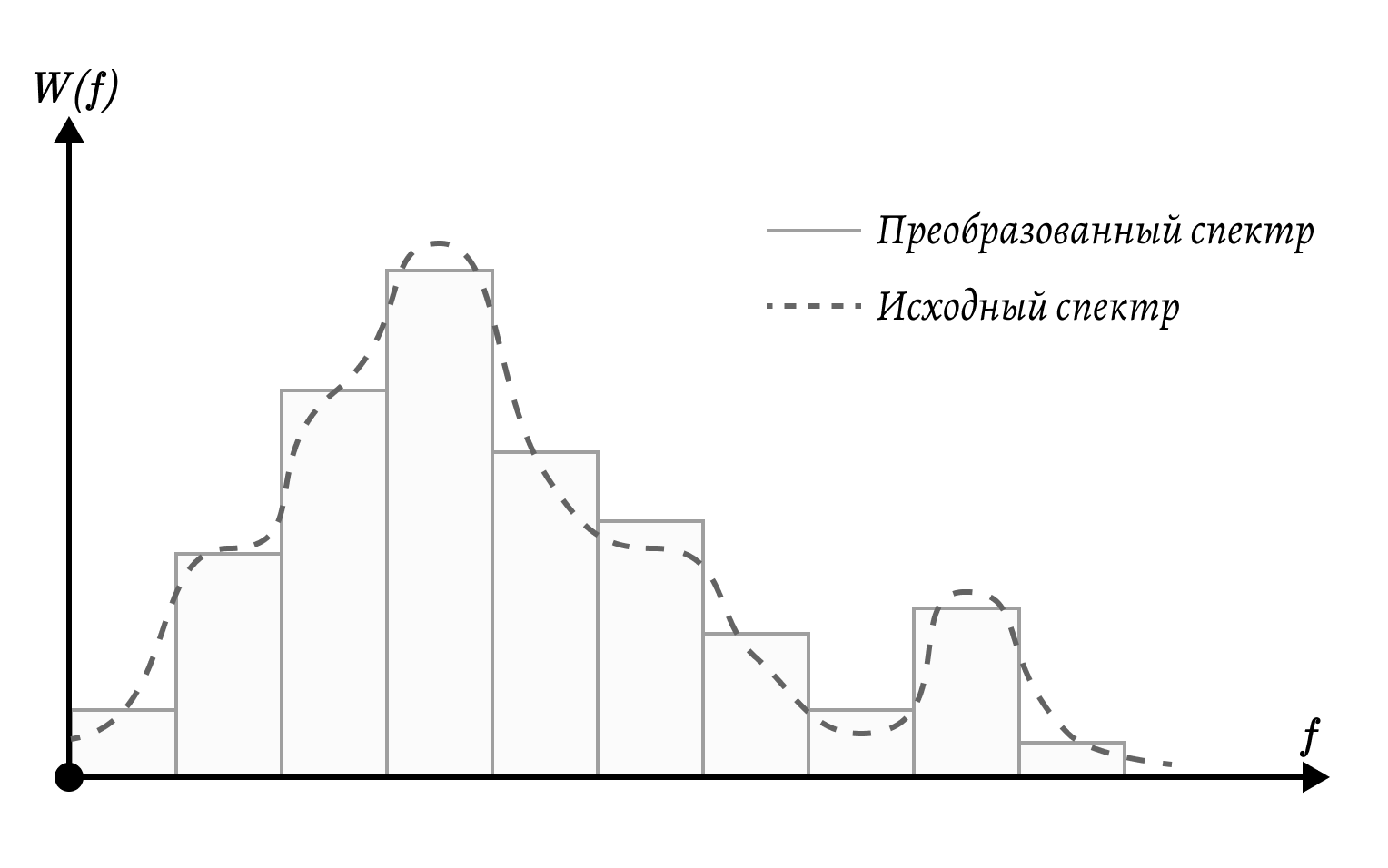Взяли кривую распределения энергии по частотам и побили на гистограмму, изверги

Вокодер — это довольно впечатляющая технология: он может сжимать звук больше, чем в 2–3 раза, при приемлемых уровнях разборчивости речи, используя наши знания о извлечении и восприятии речи человеком.

Если вы относите себя к числу энтузиастов: будь вы школьник, изучающий Python; студент, погруженный в обработку сигналов и анализ с помощью преобразования Фурье, или просто любопытствующий человек — эта статья будет вам интересна.

И теперь, когда я ответил, зачемвам может понадобиться полосный вокодер, я объясню, какможно написать его на Python. Хотя, конечно, вместе с «как?» вполне может возникнуть вопрос «что это вообще такое?». На него я тоже с радостью отвечу.

Вокодер

Самое простое объяснение заложено в самом названии. Вокодер — это устройство синтеза речи, основанное на знании механизмов ее образования и восприятия. Вокодер был изобретен физиком Хомером Дадли еще в 1928 году и изначально был разработан для экономии частотных ресурсов линии телефонной и радиосвязи при передаче речевых сигналов.

Важно отметить, что за почти столетнюю историю было придумано большое количество подкатегорий вокодеров. Они характеризуются различным звучанием (более человечный, или как жестяная банка), разборчивостью речь (иногда различимы лишь отдельные слоги, а не слова), сжатием аудиопотока.

Речевые сигналы

Пример речевого сигнала длительностью 10 мс

Речевой сигнал — это информация, представленная в виде устной речи, которая по сути является звуковыми колебаниями. Мы привыкли думать, что производим речь ртом. На деле же в процессе звукоизвлечения участвуют почти все органы выше диафрагмы. Даже наш череп по сути является совокупностью маленьких резонаторов. Весь произносительный аппарат человека определяет: будете вы звучать приятным тенором и бойким альтом.

Звуки речи подразделяются на шумы и тоны: тоны в речи возникают в результате колебания голосовых складок (они же связки); шумы же образуются в результате непериодических колебаний выходящей из легких струи воздуха. Обычно тоны — это гласные, почти все глухие согласные — шумы, а звонкие согласные сочетают в себе и шумы и тоны, потому что образуются путем их слияния. Шумы и тоны могут различаться по высоте, тембру, силе и многим другим характеристикам.

Избыточность речи необходима для передачи эмоционального состояния и экспрессивности человека.

Когда человек говорит, он производит спектрально-временную модуляцию широкополосного сигнала, генерируемого голосовыми складками и представляющего своего рода несущую. Полезная информация в этой несущей есть только в интонации, т.е. в изменении частоты основного тона, и в смене вида спектра с тонального на шумовой и наоборот.

Классический вокодер же как раз занимается тем, что передает не весь речевой сигнал, а только значения его определенных параметров, которые на приемной стороне управляют синтезатором речи. Основу синтезатора речи составляют:

генератор тонального сигнала для формирования гласных звуков
генератор шума для формирования согласных звуков
система формантных фильтров для воссоздания индивидуальных особенностей голоса

Полосный вокодер

Мы будем работать именно с ним. В полосном вокодере используется нечувствительность органов слуха к фазе сигнала. То есть, если мы подсунем нашему уху звуковой сигнал длительностью сравнимой с длительностью типичной фонемы, то информация будет извлечена только благодаря схожему спектру (распределению энергии по частотам) и длительности.

С использованием полосного вокодера человеческая речь остается разборчивой даже после всех преобразований, хотя голос и становится похожим на «голос робота». Но — опять же — если вы будете использовать полосный вокодер для своих музыкальных экспериментов, «голос робота» может быть очень кстати.

Что ж, теперь, когда я ответил на вопрос «что?» и закончил с теорией, мы можем переходить к практике.

План

Раскромсать сигнал на маленькие отрезки
Каждый из отрезков сжать используя преобразования в частотной области
Восстановить сигнал на принимающей стороне
Склеить все восстановленные отрезки в единый сигнал

Оконная функция

Оконная функция Хэмминга

Мы будем использовать функцию Хэмминга. Хотя, конечно, можно использовать, например, и оконную функцию Барлетта (треугольное преобразование). В ходе экспериментов оказалось, что выбор оконной функции оказывает незначительный эффект на разборчивость речи.

Оконная функция нужна нам для того, чтобы поделить сигнал на маленькие кусочки
по 50 мс. При этом, эти кусочки смещены на 50% от длины так, что накладываются друг на друга. Этот параметр можно регулировать.

Если умножить соответствующие значения сигнала на эти оконные функции, то можно получить пачки данных:

Чтобы собрать сигнал обратно, нам просто нужно сложить соответствующие части сигнала вместе:

Результат может немного отличаться от оригинала на краях, поскольку мы убрали часть сигнала первым и последним окном, но в целом нам удалось поделить сигнал на маленькие кусочки. Они понадобятся нам в будущем.

Быстро о быстром преобразовании Фурье

Предполагаю, что читатель так или иначе уже знаком с преобразованием Фурье.

Сгенерируем сигнал, чтобы продемонстрировать подход, который мы будем использовать далее. Сигнал состоит из двух синусоид с частотами 50 Гц и 175 Гц соответственно.

$y = sin(50*2 \pi x) + \frac{3}{4}sin(175*2 \pi x)$

Разложим сигнал с помощью алгоритма быстрого преобразования Фурье для действительных чисел. Быстрое преобразование Фурье (БПФ или FFT) — это алгоритм ускоренного вычисления дискретного преобразования Фурье. Алгоритм применяют к любым коммутативным ассоциативным кольцам с единицей, к полю комплексных чисел и к кольцам вычетов. Мы же будем применять его к серии вещественных чисел, которые и представляют наш сигнал.

Возьмем модуль от результата. Поскольку результат комплексный, это будет массив чисел, который представляет собой распределение амплитуд по частотам. Получим ожидаемый спектр с двумя пиками на соответствующих частотах:

Использовав обратный алгоритм БПФ, из частотной области снова перейдем во временную:

Можно заметить, что на первый взгляд сигналы полностью отличаются друг от друга. Это связано с тем, что при взятии модуля результата БПФ мы потеряли информацию о фазе. Зато перешли от комплексных чисел к вещественным, а значит по каналу передачи информации можно будет пропустить в два раза меньше информации.

Симулируем работу вокодера и канала передачи данных

Наш входной файл называется a.wav. Это аудиофайл с частотой дискретизации 8000 Гц. На каждый семпл отводится 1 байт.

Теперь мы переходим к самому интересному: давайте разложим каждый маленький кусочек нашего файла, который мы получили ранее с помощью оконной функции.

Нас интересует диапазон от 100 Гц (условно минимальная частота основного тона) до 4000 Гц (максимальная частота различимая при частоте дискретизации 8000 Гц). Пусть экспоненциально будет увеличиваться средняя частота октавы (полосы). Зададим 63 полосы, в которых мы будем проводить накопление энергии по формуле:

$K = 1.06, F_i = 30*K^{i}$ Частотные полосы

№	Центральная частота, Гц	Нижняя граница, Гц	Верхняя граница, Гц
1	102	99.06	105.0
2	108	105.0	111.3
3	115	111.3	117.98
4	121	117.98	125.06
5	129	125.06	132.56
6	136	132.56	140.52
7	145	140.52	148.95
8	153	148.95	157.88
9	163	157.88	167.36
10	172	167.36	177.4
11	183	177.4	188.04
12	194	188.04	199.33
13	205	199.33	211.28
14	218	211.28	223.96
15	231	223.96	237.4
16	244	237.4	251.64
17	259	251.64	266.74
18	275	266.74	282.75
19	291	282.75	299.71
20	309	299.71	317.69
21	327	317.69	336.76
22	347	336.76	356.96
23	368	356.96	378.38
24	390	378.38	401.08
25	413	401.08	425.15
26	438	425.15	450.65
27	464	450.65	477.69
28	492	477.69	506.36
29	521	506.36	536.74
30	553	536.74	568.94
31	586	568.94	603.08
32	621	603.08	639.26
33	658	639.26	677.62
34	698	677.62	718.28
35	740	718.28	761.37
36	784	761.37	807.05
37	831	807.05	855.48
38	881	855.48	906.81
39	934	906.81	961.21
40	990	961.21	1018.89
41	1049	1018.89	1080.02
42	1112	1080.02	1144.82
43	1179	1144.82	1213.51
44	1249	1213.51	1286.32
45	1324	1286.32	1363.5
46	1404	1363.5	1445.31
47	1488	1445.31	1532.03
48	1577	1532.03	1623.95
49	1672	1623.95	1721.39
50	1772	1721.39	1824.67
51	1879	1824.67	1934.15
52	1991	1934.15	2050.2
53	2111	2050.2	2173.21
54	2237	2173.21	2303.61
55	2372	2303.61	2441.82
56	2514	2441.82	2588.33
57	2665	2588.33	2743.63
58	2825	2743.63	2908.25
59	2994	2908.25	3082.74
60	3174	3082.74	3267.71
61	3364	3267.71	3463.77
62	3566	3463.77	3671.6
63	3780	3671.6	3891.89

Теперь, после разложения в спектр, мы можем подробнее рассмотреть результат и выделить суммарную мощность в каждой из полученных полос.

Таким образом по каналу передачи данных на каждую пачку информации в отдельном нарезанном окне мы будем передавать 63 байта: по 1 байту на каждую частотную полосу — или, как ее еще можно называть, октаву.

При восстановлении мы применяем накопленную мощность к центральной частоте соответствующей полосы. Остальные части спектра мы оставим нулевыми. Очевидно, что спектры будут немного отличаться друг от друга, но это приемлемая разница для разборчивого речевого сигнала.

После того, как мы проведем череду таких преобразований к каждой пачке информации, мы получим наборы восстановленных пачек данных. Склеив их, мы увидим восстановленный аудиосигнал:

Теперь мы можем сохранить его в b.wav, и вуаля! Мы написали полосный вокодер на Python и получили достаточно хорошее сжатие речи.

В итоге, нам удалось добиться коэффициента сжатия около 3.73, то есть мы сжали сигнал на 60–70% с сохранением разборчивости речи. Многие из описанных в статье преобразований имеют коэффициенты, изменяя которые можно получить еще более впечатляющие результаты. Например, вы можете поменять коэффициенты количества октав, длительности окна, сдвига окон относительно друг друга и частоты дискретизации сигнала.

Вы можете послушать примеры сигналов и Jupyter Notebook в репозитории проекта. Попробуйте поэкспериментировать с ним, например положив в корень файл со своим голосом, и запустив скрипт.

Надеюсь, эта статья была увлекательной, а главное вы убедились, насколько легко можно работать в прикладном ключе с такими «научными» алгоритмами как БПФ.