Свойства высокоразмерных пространств, которые применяются в машинном обучении22.12.2022 15:47

В данной статье описываются уникальные свойства высокоразмерных пространств и алгоритмы машинного обучения, которые основываются на них, и не страдают от экспоненциального роста сложности. Использование высокоразмерных пространств влечет большие вычислительные затраты. Потому что, при увеличении размерности наблюдается экспоненциальный рост необходимых данных или шагов итерационного алгоритма необходимых для достижения заданной точности. Часто этот эффект называют проклятием размерности и рекомендуют минимизоровать размерность и сложность моделей.

1. Введение

«Проклятие размерности» — проблема, связанная с экспоненциальным возрастанием количества данных из-за увеличения размерности пространства. Термин «проклятие размерности» введен Ричардом Беллманом [1] в 1961 году. Этот эффект возникает в задачах математического моделирования вычислительных методах. В задачах машинного обучения также встречается этот эффект. В качестве примера рассмотрим метод ближайших соседей [2], который используется для решения задачи классификации. Объекты относятся к классу, которому принадлежит большинство из его ближайших соседей в пространстве признаков. Для качественной работы этого метода должна быть достигнута достаточная плотность объектов в пространстве. Рассмотрим, как связаны размерность пространства, плотность объектов и их число. Возьмем единичный интервал [0,1] , тогда 100 равномерно разбросанных точек будет достаточно, чтобы покрыть этот интервал с частотой не менее 0.01 . Но когда перейдем на 10-мерный куб. Для достижения той же степени покрытия потребуется уже $10^{20}$ точек. То есть, по сравнению с одномерным пространством, требуется в $10^{18}$ раз больше точек. Именно по этой причине переборные алгоритмы являются крайне неэффективными в задачах машинного обучения.

При описанном выше минусе больших размерностей невозможно использовать небольшое число параметров и достигать хороших результатов. Методы глубокого обучения, где используют перепараметризованные модели, жертвуют вычислительной сложностью и стабильностью обучения, но при этом достигают значительного прироста в качестве модели.

В секции 2 мы дадим общее описание методов работы с высокоразмерными пространствами. В 2.1 теоретически покажем почему эти методы работают, главным выводом этой главы будет формула (2). А в секции 2.2 обсудим, что значит семантическая сумма двух объектов и как это описать в терминах математики и рассмотрим примеры применения этих идей в части 3.

2. Свойства высокоразмерных пространств

Существуют методы работы с высокоразмерными пространствами построенные на Vector Symbolic Architectures (о них будет рассказано дальше) и Hyperdimensional computing. Данное направление развивалась до 2020 года под разными прикладными применениями, такими как фильтр Блума [3], Random Projections[4] и прочими, но при этом математическая основа у них одна: теория концентрация меры (concentration of measure). Основной принцип этой теории упрощенно формулируется следующим образом: «Случайная величина, которая зависит от многих независимых переменных (но не слишком сильно ни от одной из них), по существу постоянна».

2.1 Независимость случайных векторов

Рис. 1 Пример двух случайных векторов в 3-мерном пространстве. Рис. 1 Пример двух случайных векторов в 3-мерном пространстве.

Возьмем две случайные точки в пространстве. В качестве меры сходства двух векторов будем использовать их корреляцию или косинусное сходство, что соответствует косинусу угла между ними. Тогда распределение угла между ними будет:

$P(\theta) = \frac{\Gamma(\frac{d}{2})}{\Gamma(\frac{1}{2})\Gamma(\frac{d-1}{2})} \cdot \sin(\theta)^{d-2}, \tag*{(1)}$

где $\Gamma$ — гамма функция и $\theta$ определена на отрезке $[0, \pi]$ . На рис. 2 изображена плотность распределения.

Немного про Гамма функцию и как ее понимать. Рис. 2 Плотность распределения угла (в градусах) между двумя случайными векторами в d-мерном пространстве. Рис. 2 Плотность распределения угла (в градусах) между двумя случайными векторами в d-мерном пространстве.

Ключевым для распределения описанного в (1) будет:

$E(\cos(\theta)) = 0, \quad Var(\cos(\theta)\sim(1/d). \tag*{(2)}$

Поэтому в высокоразмерном пространстве случайные вектора имеют нулевой косинус с очень большой вероятностью. А с увеличением размерность эта вероятность быстро растет. Также можно показать, что сумма векторов будет коррелировать с каждым из них, потому что для двух нормированных векторов $\mathbf{a}$ и $\mathbf{b}$ верно:

$(\mathbf{a} + \mathbf{b})^T\mathbf{a} = \mathbf{a}^T\mathbf{a} + \mathbf{b}^T\mathbf{a} \approx \mathbf{a}^T\mathbf{a} = 1. \tag*{(3)}$

2.2 Семантика векторов

Если рассматривать векторное пространство как пространство векторных представлений, в которое проецируется некоторое множество объектов. То одним из требований к такой проекции является сохранение семантической связи между объектами, например, это значит, что похожие объекты лежат рядом. Также плюсом будет возможность задать операции между векторными представлениями так, чтобы они имели свой семантический смысл. Например, у нас есть два изображения, которые мы хотим объединить т.е. получить их семантическую сумму, которая будет арифметической суммой соответствующих векторов.

Проведем мысленный эксперимент, какой должны быть семантическая сумма двух изображений. Пусть есть рисунок свиньи с круглыми формами, хвостом и четырьмя ногами Рис. 3 (а). Пусть также есть рисунок грузовика с квадратными формами, колесами и одним окном в кабине Рис. 3 (б). Тогда семантической суммой назовем изображение Рис. 3 (в), в котором есть атрибуты от свиньи и от грузовика. Т.е. оно одновременно похоже на каждое из слагаемых.

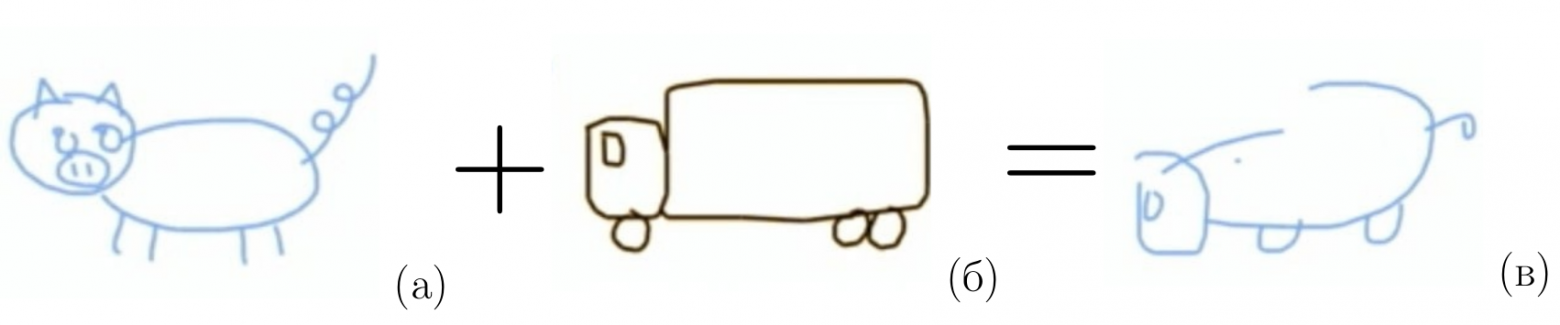Рис. 3 Пример объединения семантики двух изображений. Пусть есть рисунок свиньи с круглыми формами, хвостом и четырьмя ногами (а). Пусть также есть рисунок грузовика с квадратными формами, колесами и одним окном в кабине (б). Тогда семантической суммой назовем изображение (в), в котором есть атрибуты от свиньи и от грузовика. Т.е. оно одновременно похоже на каждое из слагаемых. Рис. 3 Пример объединения семантики двух изображений. Пусть есть рисунок свиньи с круглыми формами, хвостом и четырьмя ногами (а). Пусть также есть рисунок грузовика с квадратными формами, колесами и одним окном в кабине (б). Тогда семантической суммой назовем изображение (в), в котором есть атрибуты от свиньи и от грузовика. Т.е. оно одновременно похоже на каждое из слагаемых.

Вернемся к высокоразмерным пространствам. Пусть мы построили соответствие между векторами высокоразмерного пространства и объектами, например, изображениями. Причем в данном случае достаточно равномерно заполнить пространство, так чтобы выполнялась формула (1). Тогда условие на сохранение семантической связи будет автоматически выполнено, потому что каждый уникальный объект отличается от любого другого, а значит сходство (корреляция) его со всеми остальными будет 0. Рассмотрим сумму двух объектов, по формуле (3) получаем, что сумма двух абсолютно разных объектов одновременно похожа на первый и на второй объекты, что мы и хотели получить в мысленном эксперименте.

Допустим мы хотим собрать объект из семантических блоков, например, собрать картинку свиньи. У этой свиньи должен быть завернутый хвостик, круглое тело, видно четыре ноги и так далее. Каким образом можно это закодировать? Для начала рассмотрим хвостик, для него введем вектор, который выполняют роль ключа $k_{tail}$ . Для каждого типа хвоста введем коды, также из высокоразмерного пространства, $v^{tail}_1, v^{tail}_2, \dots$ которые описывают сам хвостик. Проведем такую процедуру для всех оставшихся блоков: тело (body), ноги (legs). Тогда итоговый вектор описывающий данную свинью будет:

$\mathbf{a} = k_{tail}\otimes v^{tail}_i + k_{body}\otimes v^{body}_j + k_{legs}\otimes v^{legs}_l, \tag*{(4)}$

где $\otimes$ означает поточечное умножение векторов. Заметим, что если есть два вектора полученных по формуле выше, то их сумма будет соответствовать вектору составленному из сумм соответствующих кодов:

$\begin{multline*} (k_{tail}\otimes v^{tail}_i + k_{body}\otimes v^{body}_j + k_{legs}\otimes v^{legs}_l) + \\ + (k_{tail}\otimes v^{tail}_p + k_{body}\otimes v^{body}_q + k_{legs}\otimes v^{legs}_r) = \\ = k_{tail}\otimes (v^{tail}_i + v^{tail}_p) + k_{body}\otimes (v^{body}_j + v^{body}_q) + k_{legs}\otimes (v^{legs}_l + v^{legs}_r) \end{multline*}$

3 Примеры применения

3.1 Language Geometry using Random Indexing

Данная работа [5] посвящена задачи классификации языка по тексту. Авторы описывают метод кодирования буквенных N-грамм в многомерные языковые векторы. и показывают, что метод легко реализуется и не требует большой вычислительной мощности. Такой подход достигает точности 97,4%, сравнимой с современными методами.

Авторы предлагают кодировать каждую букву вектором из d-мерного пространства (d = 10000), который имеет равное количество случайно расположенных 1 и -1. Такие векторы используются для представления основных элементов системы, которыми являются 26 букв латинского алфавита и пробел (ASCII). Авторы также используют операции над векторами: сложение, умножение и сдвиг на 1 (т.е. смещение всех координат на 1 вправо).

Вектор триграммы собиратся из векторов букв образовывающих ее. Например, $ABC = \rho\rho A*\rho B*C$ . Вектором слова будет сумма всех его триграмм. Вектором языка это сумма всех слов языка. Также для двух слов V_1 и V_2 верно:

$\begin{align*} V_1 = \rho\rho A*\rho B*C \\ V_2 = \rho\rho A*\rho C*B \end{align*}$ $\Longrightarrow cos(V_1, V_2) \approx \rho\rho (A*A)*\rho(B*C) * (B*C) \approx 0\\$ Рис. 4 10 000-мерные языковые векторы для 21 языка группируются на основе известных отношений между языками. Языковые векторы были основаны на буквенных триграммах и проецировались на плоскость с помощью t-SNE. Рис. 4 10 000-мерные языковые векторы для 21 языка группируются на основе известных отношений между языками. Языковые векторы были основаны на буквенных триграммах и проецировались на плоскость с помощью t-SNE.

Таким образом авторы получили простой в реализации, быстрый алгоритм классификации языков, который имеет достаточно высокую точность. Также данный метод позволяет работать с семантикой языков, например, кластеризовать их на языковые группы.

3.2 Unpaired Image Translation via Vector Symbolic Architectures

В работе [6] авторы предложили метод перевода изображений из одного типа в другой и взяли за основу принципы VSA. Мы не будем полностью разбирать идею, покажем только как авторы использовали высокоразмерное пространство.

Задача перевода изображений заключается в том, что нужно научиться преобразовывать картинку при этом сохранять общий смысл. Например для изображения лица, можно создать похожее на него, но как будто его нарисовала анимационная студия. При этом лица на двух изображениях будут иметь множество схожих черт. Получаемый стиль, в нашем случае «анимационный» стиль, называют целевым.

Авторы поясняют идею следующим образом, пусть есть вектор исходного изображения $v_{src}.$ Этот вектор имеет высокую размерность и состоит только из $\{0, 1\}$ . При этом формула (2) остается верной.

$v_{src} = c \otimes c_{src} + p \otimes p_{src},$

где и ~--- вектора, представляющие автомобиль и пешехода, связанные с векторами $c_{src}$ и $p_{src}$ , специфичными для источника, соответственно.

Далее нужно создать связку-вектор, который может отсоединить эти атрибуты, специфичных для источника, и привязать атрибуты, специфичные для целевого стиля.

$\begin{align*} v_{src} \otimes u_{src\leftrightarrow tgt} &\approx v_{tgt}, \\ \text{где } u_{src\leftrightarrow tgt} &= (c_{src} \otimes c_{tgt} + p_{src} \otimes p_{tgt}) \end{align*}$

В итоге процедура получения векторов в целевом стиле выглядит как:

$\begin{align*} v_{src} \otimes u_{src\leftrightarrow tgt} &= c \otimes c_{src} \otimes (c_{src} \otimes c_{tgt} + p_{src} \otimes p_{tgt}) \\ &+ p \otimes p_{src} \otimes (c_{src} \otimes c_{tgt} + p_{src} \otimes p_{tgt}) \\ &= ( c \otimes c_{tgt} + \text{шум}) + ( p \otimes p_{tgt} + \text{шум}) \\ &= c \otimes c_{tgt} + p \otimes p_{tgt} + \text{шум} \approx v_{tgt} \end{align*}$ Рис. 5 Примеры переводов изображений GTA в стиль городских пейзажей. Мы видим, что идея авторов позволяет успешно переводить изображения, в частности, данный метод способен распознавать определенные текстуры и атрибуты (например, серый булыжник, белые полосы движения, а не желтые), которые обычно встречаются на изображениях городских пейзажей. Рис. 5 Примеры переводов изображений GTA в стиль городских пейзажей. Мы видим, что идея авторов позволяет успешно переводить изображения, в частности, данный метод способен распознавать определенные текстуры и атрибуты (например, серый булыжник, белые полосы движения, а не желтые), которые обычно встречаются на изображениях городских пейзажей.

4. Резюме

Мы начали рассказ с того, что высокоразмерные пространства доставляют трудности в многих вычислительных задачах (пример с 10-мерным кубом). Далее рассмотрели с точки зрения математики некоторые свойства случайных векторов и вывели основную формулу (2), которая является основой описанных выше методов. Затем обсудили идею как нужно использовать это свойство и как с этим связана семантика объектов. После этого рассмотрели примеры применения. Разобрали алгоритм построения векторного описания языка и задачу перевода изображений.

[1] Bellman, R.E. 1961. Adaptive Control Processes. Princeton University Press, Princeton, NJ.
[2] Fix, Evelyn; Hodges, Joseph L. (1951). Discriminatory Analysis. Nonparametric Discrimination: Consistency Properties.
[3] Blustein, James; El-Maazawi, Amal (2002), «optimal case for general Bloom filters», Bloom Filters — A Tutorial, Analysis, and Survey, Dalhousie University Faculty of Computer Science, pp. 1–31.
[4] Ella, Bingham; Heikki, Mannila (2001). «Random projection in dimensionality reduction: Applications to image and text data».
[5] Aditya Joshi, Johan Halseth, and Pentti Kanerva (2014) «Language recognition using random indexing».
[6] Justin Theiss, Jay Leverett, Daeil Kim, Aayush Prakash (2022) «Unpaired Image Translation via Vector Symbolic Architectures».