Вычисление весового спектра линейного подпростанства в Wolfram Mathematica

Процесс вычисления весового спектра
Первопричина
Данная статья обязана своим появлением одному достаточно давнему вопросу, который был задан в группе русскоязычной поддержки Wolfram Mathematica. Однако, ответ на него сильно разросся и в итоге стал жить самостоятельной жизнью и даже обзавелся собственными проблемами. Как понятно из названия статьи, задача была посвящена вычислению весового спектра, а значит напрямую относится к дискретной математике и линейной алгебре. Здесь же демонстрируется решение на языке программирования Wolfram Language. Не смотря на то, что суть задачи очень проста (для простых базисных векторов она вполне решается в уме), гораздо больший интерес представляет процесс оптимизации алгоритма нахождения весового спектра. Авторы придерживаются мнения, что рассматриваемая в данной статье задача и способы ее решения очень хорошо показывают способы применения таких приемов в языке Wolfram как компиляция и параллелизация. Таким образом основная цель, это показать один из эффективных способов ускорения кода в Mathematica.
Формулировка
Процитируем первоначальную формулировку задачи:
a) Назовем вектором строку битов (значения 0 или 1) фиксированной длины N: то есть, всего возможно 2N различных векторов.
b) Введем операцию сложения по модулю 2 векторов (операция xor), которая по двум векторам a и b получает вектор a + b той же длины N.
c) Пусть дано множество A = {ai | i ∈ 1…K} из 0 ≤ K ≤ 2N векторов. Назовем его порождающим: при помощи сложения ai множества A можно получить 2K векторов вида ∑i=1…Kbiai, где bi равно либо 0, либо 1.
d) Весом вектора назовем количество единичных (ненулевых) битов в векторе: то есть, вес — это натуральное число от 0 до N.
Требуется для заданных порождающих множества векторов и числа N построить гистограмму (спектр) количества различных векторов по их весу.
Формат входных данных:
Текстовый файл из набора строк одинаковой длины по одному вектору в строке (символы 0 и 1 без разделителей).Формат выходных данных:
Текстовый файл с парой значений вес/количество разделенных символом табуляции, по одной паре на строку, сортированный по числовому значению веса.
Решение вручную
Для начала попробуем решить задачу в уме, чтобы понять принцип подсчета весового спектра. Для этого будем использовать векторы минимальной длины. Затем потребуется всего лишь расширить алгоритм для любого количества векторов и любой размерности. Пусть дан базис из двух векторов по два элемента в каждом:
basis = {{0, 1}, {1, 1}}
Так как векторов всего два, то всех возможных линейных комбинаций и, соответственно, комбинаций значений bi будет 2K, где K — количество базисных векторов. Получаем 4 следующие линейные комбинации:
mod2(0 * {0, 1}, 0 * {1, 1}) = {0, 0}
mod2(0 * {0, 1}, 1 * {1, 1}) = {1, 1}
mod2(1 * {0, 1}, 0 * {1, 1}) = {0, 1}
mod2(1 * {0, 1}, 1 * {1, 1}) = {1, 0}
Здесь предполагается, что функция сложения по модулю два уже определена должным образом. Получилось четыре вектора, размерность каждого при этом равна двум. Чтобы наконец вычислить спектр нужно просто посчитать число единиц в каждом получившемся векторе, то есть:
sum({0, 0}) = 0
sum({1, 1}) = 2
sum({0, 1}) = 1
sum({1, 0}) = 1
Посчитаем количества вхождений в получившийся список каждого веса. И тогда согласно требованиям задачи, результат должен выглядеть следующим образом:
{{0, 1}, {1, 2}, {2, 1}}
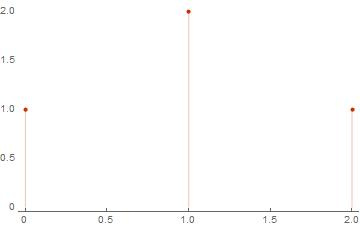
Реализация простого алгоритма в Wolfram Mathematica
Итак, теперь все то, что было проделано в уме попробуем записать и автоматизировать при помощи Wolfram Language. Для начала создадим функцию, выполняющую сложение по модулю 2 (как и было сказано в условии задачи):
(* сложение пары бит *)
mod2[b1_Integer, b2_Integer] := Mod[b1 + b2, 2]
(* сложение произвольного числа бит *)
mod2[b1_Integer, b2__Integer] := mod2[b1, mod2[b2]]
(* расширение функции для работы со списками бит - векторами *)
Attributes[mod2] := {Listable}
Следующая функция должна принимать на вход список векторов и список коэффициентов bi — вектор, длина которого равна числу векторов в базисе. Возвращать вектор той же размерности что и элементы базиса — линейная комбинация.
(* вычисление линейной комбинации с проверкой длины базиса *)
combination[basis: {{__Integer}..}, b: {__Integer}] /;
Length[basis] == Length[b] :=
Apply[mod2, Table[basis[[i]] * b[[i]], {i, 1, Length[b]}]]
Теперь нужно получить список всех возможных наборов коэффициентов bi. Очевидно, что их количество равно 2K, а все возможные наборы — это просто запись всех чисел от 0 до 2K-1 в двоичном представлении. Тогда список всех возможных линейных комбинаций можно получить так:
linearCombinations[basis: {{__Integer}..}] :=
With[{len = Length[basis]},
Table[combination[basis, IntegerDigits[i, 2, len]], {i, 0, 2^len - 1}]
]
Результат выполнения функции выше — список длиной 2K векторов. Все что нам остается сделать — это посчитать вес каждого вектора в этом списке, а затем подсчитать число встреч каждого веса:
weightSpectrum[basis: {{__Integer}..}] :=
Tally[Map[Total, lenearCombination[basis]]];
Проверим как это будет работать. Создадим базис из списка случайных векторов и подсчитаем весовой спектр:
(* проверка вычислений *)
basis = RandomInteger[{0, 1}, {6, 6}]
ws = weightSpectrum[basis]
ListPlot[ws, PlotTheme -> "Web"]
(* Out[..] := {{0, 0, 1, 1, 1, 0}, {1, 0, 0, 0, 0, 1}, {1, 1, 0, 1, 0, 1},
{1, 0, 0, 1, 1, 0}, {1, 0, 0, 0, 1, 1}, {0, 1, 0, 1, 1, 1}}
Out[..]:= {{0, 1}, {4, 15}, {3, 20}, {2, 15}, {1, 6}, {5, 6}, {6, 1}} *)
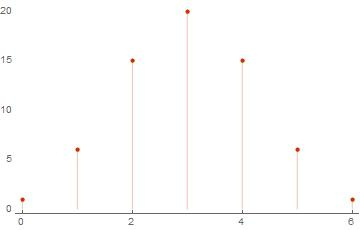
Но что будет, если попытаться посчитать все тоже самое, но для большего количества векторов? Воспользуемся функцией AbsoluteTiming[] и посмотрим как себя ведет зависимость времени расчета от размера базиса.
basisList = Table[RandomInteger[{0, 1}, {i, 10}], {i, 1, 15}];
timeList = Table[
{Length[basis], First[AbsoluteTiming[weightSpectrum[basis]]]},
{basis, basisList}
];
ListPlot[timeList, PlotTheme -> "Web", Joined -> True]
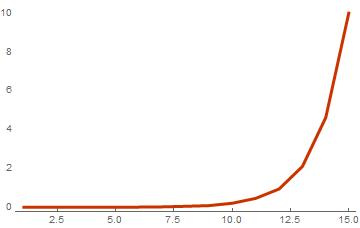
Зависимость времени расчета от размера базиса при одинаковой длине векторов
Как видно на получившемся графике, время расчета увеличивается по экспоненте вместе с добавлением числа векторов в базис. Получается что для базиса из 15 векторов, где по 10 элементов в каждом, вычисление спектра длится около 10 секунд. Такое время расчета достаточно большое, но ничего удивительного в этом нет, так как выше уже было сказано, что количество линейных комбинаций растет по экспоненте вместе с ростом размера базиса, а значит и число операций увеличивается с той же скоростью. Еще одним фактором, который понижает скорость вычислений является то, что код не оптимален. Wolfram Language — интерпретируемый язык программирования и поэтому изначально не считается достаточно быстрым, а значит стандартные функции не дадут нам максимальной производительности. Для решения этой проблемы воспользуемся компиляцией.
Использование скомпилированных функций
Коротко о Compile
Синтаксис этой функции достаточно прост и очень похож на Function. В качестве результата Compile всегда возвращает «объект» — скомпилированную функцию, которая может быть применена к числовым значениям или спискам чисел. Compile не поддерживает работу со строками, символами или составными выражениями Wolfram Language (кроме выражений состоящих из List). Ниже приведено несколько примеров создания скомпилированных функций.
cSqr = Compile[{x}, x^2];
cSqr[2.0]
(* Out[..] := 4.0 *)
cNorm = Compile[{x, y}, Sqrt[x^2 + y^2]];
cNorm[3.0, 4.0]
(* Out[..] := 5.0 *)
cReIm = Compile[{{z, _Complex}}, {Re[z], Im[z]}];
cReIm[1 + I]
(* Out[..] := {1.0, 1.0} *)
cSum = Compile[{{list, _Real, 1}}, Module[{s = 0.0}, Do[s += el, {el, list}]; s]];
cSum[{1, 2, 3.0, 4.}]
(* Out[..] := 10.0 *)
Все доступные опции и более подробные примеры можно посмотреть в официальной документации по ссылке выше. Теперь же перейдем непосредственно к функции для вычисления весового спектра.
Компиляция вычисления весового спектра
Как и в простом случае, можно создать несколько простых функций, а затем применять их по очереди для получения результата. А можно выполнять все операции в теле всего лишь одной функции. И тот и другой способ вполне могут быть реализованы. Мы ради разнообразия пойдем по второму пути.
cWeightSpectrumSimple =
Compile[
{{basis, _Integer, 2}},
Module[
{
k = Length[basis],
spectrum = Table[0, {i, 0, Last[Dimensions[basis]]}]
},
Do[
With[
{
(* вычисление веса одной из 2^k - 1 комбинаций *)
weight = Total[Mod[Total[IntegerDigits[b, 2, k] * basis], 2]] + 1
},
(*
Размер списка spectrum равен максимально возможному весу.
переменная weight на каждой итерации - это вес линейной комбинации
таким образом здесь мы увеличиваем на 1 элемент списка,
индекс которого равен вычисленному только что весу.
В результате spectrum содержит сразу же весовой спектр.
Такой способ подсчета очень похож на алгоритм сортировки
подсчетом, что уже экономит значительное количество операций.
*)
spectrum[[weight]] = spectrum[[weight]] + 1
],
{b, 0, 2^k - 1}
];
Return[Transpose[{Range[0, Last[Dimensions[basis]]], spectrum}]]
]
]
Как всегда проведем небольшой тест правильности работы этой функции. Точно также возьмем список случайных базисов с размерами от 2 до 15 векторов, где каждый вектор состоит из 10 элементов и попробуем посчитать время за которое происходит подсчет весового спектра:
basisList = Table[RandomInteger[{0, 1}, {i, 10}], {i, 2, 15}];
timeList=Table[{Length[basis],First[AbsoluteTiming[cWeightSpectrumSimple[basis]]]},{basis,basisList}];
ListLinePlot[timeList, PlotTheme -> "Web"]
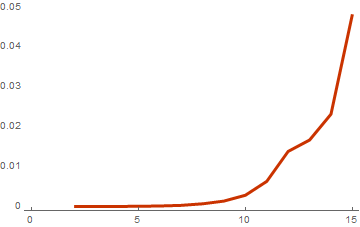
Как видно из последнего графика — разница с результатом из предыдущей части огромна. Небольшая оптимизация алгоритма в виде оптимального подсчета веса на последнем этапе и использование компиляции приводит к ускорению в 200 раз! Этот результат интересен тем, что с одной стороны он показывает Mathematica как достаточно быстрый язык, при правильном применении, а с другой — в очередной раз доказывает, что Mathematica из-за интерпретируемости является медленным языком, если не знать тонкостей внутренней работы функций.
Кода Грея
О Коде Грея
Во время размышлений над способом решением задачи возникла простая мысль. Если вдруг очередное значение bi равно нулю, то вообще нет необходимости умножать базисный вектор на это число и прибавлять его. Те векторы, которые перемножаются с нулевыми значениями не меняют результат. Сначала это показалось отлично мыслью и она даже заработала. Ведь во время перебора элементов списка bi просто выходило меньше операций сложения векторов. Затем пришла следующая идея. Вычитание и сложение векторов при вычислении линейной комбинации ничем не отличается. Это значит, что выполнимо следующее:
1 * {0, 1} + 0 * {1, 0} + 1 * {1, 1} == {0, 1} + {1, 1}
{0, 1} + {1, 1} == {1, 0} -> {1, 0} + {1, 1} == {0, 1}
То есть прибавление вектора к промежуточной сумме ничем не отличается от вычитания. И тут все сложилось в отличную идею! Что если вдруг окажется так, что в цикле по списку bi разница между представлением bk и bk+1 всего в нескольких битах? Тогда можно получить линейную комбинацию с номером k и прибавить к ней только те базисные вектора, индекс которых совпадает с номерами отличающихся бит между k и k+1. Результатом будет линейная комбинация k+1. А что если пойти еще дальше? Вдруг окажется так, что разница между соседними линейными комбинациями всего в одном векторе? Если строить прямую последовательность от 0 до 2N-1 — то это невозможно. Но вдруг можно перемешать и расположить эти числа в каком-нибудь другом порядке? Именно это, как оказалось, и называется Кодом Грея -последовательность чисел, в которой отличие между соседями всего в одном разряде. В Википедии описан один из бесконечного множества кодов — зеркальный Код Грея и метод по его получению. Ниже представлен пример такой последовательности:
| Decimal | Binary | Gray | Gray as decimal |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 001 | 1 |
| 2 | 010 | 011 | 3 |
| 3 | 011 | 010 | 2 |
| 4 | 100 | 110 | 6 |
| 5 | 101 | 111 | 7 |
| 6 | 110 | 101 | 5 |
| 7 | 111 | 100 | 4 |
Использование в скомпилированной функции
Использование компиляции уже значительно ускоряет подсчет весового спектра, теперь попробуем использовать код Грея и оптимизировать сложение векторов линейной комбинации. Только нужно понять как вычислить позицию изменившегося бита на каждом шаге. К счастью на помощь пришла 13-ая глава вот этой книги. Целиком подсчитать линейную комбинацию потребуется лишь один раз в самом начале. Но, так как точно известно, что первая линейная комбинация — это набор нулей, то и это не потребуется. С учетом всего вышесказанного можно создать еще более оптимизированную функцию для расчета весового спектра:
WeightSpectrumLinearSubspaceGrayCodeEasy = Compile[{{basevectors, _Integer, 2}},
Module[{
n = Dimensions[basevectors][[-1]],
k = Length[basevectors],
s = Table[0, {n + 1}],
currentVector = Table[0, {n}], (*первая комбинация всегда {0, 0, ..}*)
m = 0, l = 0
},
(*точно известно, что в спектре у 0 будет вес больше или равен 1
так как первая линейная комбинация всегда является нулевым вектором*)
s[[1]] = 1;
Do[
(*позиция изменившегося бита*)
m = Log2[BitAnd[-1 - b, b + 1]] + 1;
(*здесь уже нет полного сложения векторов, а только прибавление разницы*)
currentVector = BitXor[currentVector, basevectors[[m]]];
(*подсчет веса*)
l = Total[currentVector] + 1;
s[[l]] = s[[l]] + 1,
{b, 0, 2^k - 2}
];
(* Return *) s
],
(*дополнительные опции компиляции,
вторая может использоваться только при наличии компилятора*)
RuntimeOptions -> "Speed", (*CompilationTarget -> "C",*)
CompilationOptions -> {"ExpressionOptimization" -> True}
];
Вот пример результата для базиса из 16 векторов размерностью 512:
basis = RandomInteger[{0, 1}, {16, 512}];
ListPlot[WeightSpectrumLinearSubspaceGrayCodeEasy[basis],
PlotTheme -> "Web", PlotRange -> All, Filling -> Bottom]
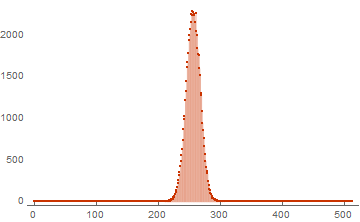
В качестве результата возвращается одномерный список весов. Такого вида список тоже вполне корректен, так как его легко привести к виду из предыдущей части. Первый элемент соответствует частоте встречи вектора нулевого веса. Последний — частоте встречи вектора из единиц. Используем тот же самый код для тестирования производительности:
basisList = Table[RandomInteger[{0, 1}, {i, 10}], {i, 2, 15}];
timeList=Table[{Length[basis],First[AbsoluteTiming[WeightSpectrumLinearSubspaceGrayCodeEasy[basis]]]},{basis,basisList}];
ListLinePlot[timeList, PlotTheme -> "Web"]
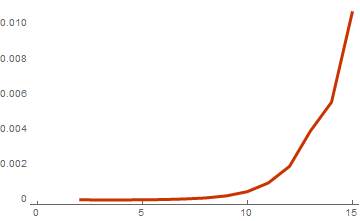
Время вычислений от размера базиса
В результате для последнего базиса из списка из 15 векторов скорость вычислений выросла еще в 5 раз. Но это немного обманчивый результат. Чтобы понять насколько повысилась эффективность необходимо посчитать отношение времени расчета для двух последних функций:
basisList = Table[RandomInteger[{0, 1}, {i, 10}], {i, 2, 20}];
timeList=Table[{
Length[basis],
First[RepeatedTiming[cWeightSpectrumSimple[basis]]] /
First[RepeatedTiming[WeightSpectrumLinearSubspaceGrayCodeEasy[basis]]]
},
{basis,basisList}
];
ListLinePlot[timeList, PlotTheme -> "Web"]
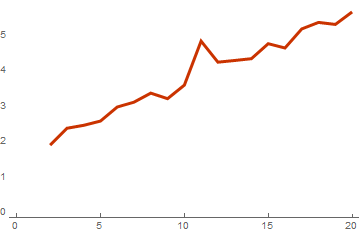
Отношение времени расчета спектра с использованием кода Грея и без
Из этого графика становится понятно, что на самом деле этот алгоритм понизил сложность вычислений на одну степень. И это будет тем заметнее и эффективнее чем больше размерность векторов в базисе. Вот такой результат получится если базис состоит из векторов с размерностью 128:
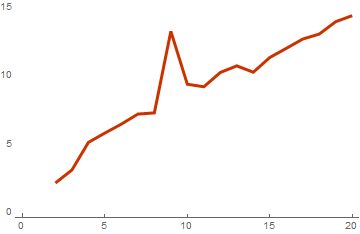
Параллелизация
Как что-то посчитать в Mathematica параллельно
В Mathematica есть небольшой набор функций, которые умеют выполнять асинхронные вычисления на разных ядрах. Только теперь надо определить с терминологией. Ведь запущенный процесс, который представляет собой что-то похожее на виртуальную машину в Mathematica тоже называется ядром, т.е. Kernel. Ядро Математики — это интерактивная среда исполнения, работающая в режиме интерпретатора. Каждое ядро занимает обязательно один процесс в системе. Потоков в привычном понимании язык не реализует. Соответственно, нужно понимать, что у ядер в стандартном использовании не будет общей памяти. В основном все функции такого типа начинают на Parallel. Самый просто способ посчитать что-то асинхронно:
ParallelTable[i^2,{i, 1, 10}]
(*Out[..] := {1, 4, 9, 16, 25, 36, 49, 64, 81, 100}*)
Подобным образом работает целый ряд функций:
ParallelMap, ParallelDo, ParallelProduct, ParallelSum, …
Есть несколько способов проверить, что это действительно выполнялось не на одном ядре. Вот так можно получить все запущенные ядра:
Kernels[]
(* Out[..] := {"KernelObject"[1, "local"], ... , "KernelObject"[N, "local"]} *)
В списке будут все запущенные на данный момент процессы. При этом они же должны отображаться и в диспетчере задач.

Два из шести процессов отвечают за запущенную сессию, а остальные — локальные ядра, которые используются для параллельных вычислений. При этом по умолчанию количество локальных ядер Mathematica совпадает с количеством физических ядер процессора. Но никто не мешает создать и большее количество. Делается это с помощью LaunchKernels[n]. В результате запускается дополнительно n ядер. А число доступных ядер процессора можно посмотреть в переменной $KernelCount.
Перечисленные в начале функции производят автоматическое распределение задач по процессам. Однако, есть способ самостоятельно отправить код выполняться на определенном ядре. Делается это при помощи ParallelEvaluate + ParallelSubmit:
ParallelEvaluate[$KernelID, Kernels[][[1 ;; 4 ;; 2]]]
(* Out[..] := {1, 3}*)
Это набора функций будет достаточно, чтобы суметь распараллелить задачу по вычислению весового спектра.
Разделение основного цикла на части
Проверим, действительно ли вычисления происходят параллельно. Для четырех физических ядер это означает что вычисление на всех четырех ядрах займет столько же времени сколько и на одном:
basis = RandomInteger[{0, 1}, {24, 24}];
AbsoluteTiming[WeightSpectrumLinearSubspaceGrayCodeEasy[basis];][[1]]
AbsoluteTiming[ParallelEvaluate[WeightSpectrumLinearSubspaceGrayCodeEasy[basis]];][[1]]
(* Out[..] := 6.518...
Out[..] := 8.790...*)
Разница во времени есть, но не четырехкратная. Значит с этим все нормально. Следующим шагом надо понять, как разделить задачу на несколько частей. Самое логичное и эффективное -вычислять только часть линейных комбинаций на каждом ядре. То есть в результате каждое ядро возвращает частичный спектр. Но как поделить список bi. Ведь он не является прямой последовательностью! В этом случае необходима функция, которая вычисляет значение из последовательности Кода Грея по индексу. Делается это вот так:
grayNum[basis_List, index_Integer] := IntegerDigits[BitXor[index, Quotient[index, 2]], 2, Length[basis]]
Grid[Table[{i, Row[grayNum[{{0, 0}, {0, 1}, {1, 1}}, i]]}, {i, 0, 7}]]
| index | code |
|---|---|
| 0 | 000 |
| 1 | 001 |
| 2 | 011 |
| 3 | 010 |
| 4 | 110 |
| 5 | 111 |
| 6 | 101 |
| 7 | 100 |
Теперь модифицируем скомпилированную функцию так, чтобы она считала только частичный спектр в определенном диапазоне индексов линейных комбинаций:
WeightSpectrumLinearSubspaceGrayCodeRange =
Compile[{{basis, _Integer, 2}, {range, _Integer, 1}},
Module[{
n = Dimensions[basis][[-1]],
k = Length[basis],
s = Table[0, {n + 1}],
currentVector = Table[0, {i, 1, Length[basis[[1]]]}],
m = 0, l = 0
},
(*вычисляем первый вектор и его вес*)
If[range[[1]] =!= 0,
currentVector = Mod[Total[basis Reverse[IntegerDigits[BitXor[range[[1]], Quotient[range[[1]] + 1, 2]], 2, k]]], 2];
];
Mod[Total[basis IntegerDigits[BitXor[range[[1]] - 1, Quotient[range[[1]] - 1, 2]], 2, k]], 2];
s[[Total[currentVector] + 1]] = 1;
Do[
m = Log2[BitAnd[-1 - b, b + 1]] + 1;
currentVector = BitXor[currentVector, basis[[m]]];
l = Total[currentVector] + 1;
s[[l]] = s[[l]] + 1,
{b, First[range], Last[range] - 1, 1}
];
(* Return *) s
],
(*дополнительные опции компиляции,
вторая может использоваться только при наличии компилятора*)
RuntimeOptions -> "Speed", (*CompilationTarget -> "C",*)
CompilationOptions -> {"ExpressionOptimization" -> True}
];
То есть, если раньше функция считала все комбинации с номерами от 0 до 2N-1, то теперь этот диапазон можно задать вручную. Теперь попытаемся придумать как разделить этот самый диапазон на равные части в зависимости от количества доступных ядер:
partition[{i1_Integer, iN_Integer}, n_Integer] :=
With[{dn = Round[(iN - i1 + 1)/n]},
Join[
{{i1, i1 + dn - 1}},
Table[{dn * (i - 1), i * dn - 1}, {i, 2, n - 1}],
{{(n - 1) * dn, iN}}
]
]
Теперь чтобы вычислить полный спектр таким образон необходимо посчитать его на каждом из отрезков, а затем все результаты сложить. Например:
WeightSpectrumLinearSubspaceGrayCodeEasy[{{1, 1}, {1, 1}, {1, 1}}]
WeightSpectrumLinearSubspaceGrayCodeRange[{{1, 1}, {1, 1}, {1, 1}}, {0, 3}]
WeightSpectrumLinearSubspaceGrayCodeRange[{{1, 1}, {1, 1}, {1, 1}}, {4, 7}]
(*
Out[..] := {4, 0, 4} =
Out[..] := {2, 0, 2} +
Out[..] := {2, 0, 2}
*)
Последним этапом нужно отправить эти вычисления на разные ядра:
WeightSpectrumLinearSubspaceGrayCodeParallel[basis: {{__Integer}..}] :=
With[{
kernels = (If[Kernels[] === {}, LaunchKernels[]]; Kernels[]),
parts = partition[{0, 2^Length[basis] - 1}, Length[Kernels[]]]
},
Total[WaitAll[Table[
ParallelEvaluate[ParallelSubmit[WeightSpectrumLinearSubspaceGrayCodeRange[basis, parts[[$KernelID]]]], kernel],
{kernel, kernels}
]]]
]
Здесь нужно внести ясность. Такая связка ParallelEvaluate + ParallelSubmit для того, чтобы в ручную контролировать то, на каком ядре будет выполняться какой участок кода. ParallelEvaluate в общем случае не может разобраться с тем, как правильно выполнять асинхронный код и делает это в итоге в один поток. А ParallelSubmit в общем случае не дает возможность точно указать нужное ядро, а выбирает его автоматически.
Проверим работает ли эта функция:
ListPlot[WeightSpectrumLinearSubspaceGrayCodeParallel[RandomInteger[{0, 1}, {16, 128}]],
PlotRange -> All, PlotTheme -> "Web", Filling -> Bottom]
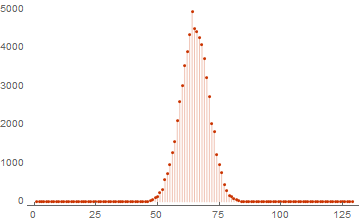
И как обычно посмотрим на разницу в скорости вычислений. Так как испоьлзуется ноутбук с 4-х ядерным процессором — ожидается ускорение примерно в 4 раза. Плюс надо учитывать время на деление задач и сложение итогового результата:
basis = RandomInteger[{0, 1}, {20, 1024}];
AbsoluteTiming[WeightSpectrumLinearSubspaceGrayCodeEasy[basis];]
AbsoluteTiming[WeightSpectrumLinearSubspaceGrayCodeParallel[basis];]
(*
Out[..] := {5.02..., Null}
Out[..] := {1.5....., Null}
*)
Естественно при наличии большего числа ядер процессора разница будет заметнее. Теперь попробуем посчитать спектр базиса побольше. Интересно сколько это займет времени? Допустим будем считать увеличивать размер базиса до тех пор, пока на один расчет не уйдет больше минуты:
spectrums = Block[{i = 1, basis, res}, Reap[
While[True,
i++;
basis = RandomInteger[{0, 1}, {i, i}];
Sow[res = AbsoluteTiming[WeightSpectrumLinearSubspaceGrayCodeParallel[basis]]];
If[res[[1]] > 60, Break[]]
]
][[-1, -1]]]
ListPlot[spectrums[[-1, -1]],
PlotLabel->Row[{"basis len: ", Length[spectrums] + 1, "; time: ", Round[spectrums[[-1, 1]], 0.01], " sec"}],
Filling->Bottom,PlotTheme->"Web",PlotRange->All]
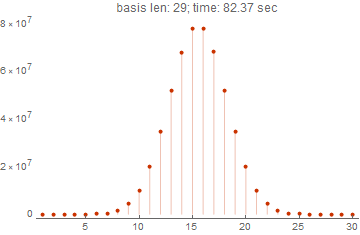
На картинке хорошо видно, что за полторы минуты функция может посчитать спектр для базиса из 29 векторов. Это очень хороший результат, при учете, что самый первый вариант, который не использует компиляцию, код Грея, параллелизацию все тоже самое вряд ли способен выполнить за разумное время. Время вычислений будет больше в тысячи раз, если даже для 15 векторов с размерностью 10 расчет занимал больше 10 секунд.
Заключение
Мне неизвестно кто и где применяет все то, что было описано в статье. Википедия говорит, что Код Грея имеет практическое назначение. Также мне известно, что вычисление спектров часто бывает связано с шифрованием и некоторыми другими задачами линейной алгебры. Но, еще раз стоит отметить, что здесь мне хотелось в первую очередь продемонстрировать пошаговое решение задачи и пошаговое применение разного рода оптимизаций: улучшение самого алгоритма, использование возможностей языка и использование аппаратных возможностей многоядерных процессоров. Я искренне надеюсь, что статья будет полезна и интересна.
P.S. Автор выражает благодарность Александру Банникову, так как именно он является инициатором в деле по поиску оптимального решения этой задачи.
