Вычисляем на видеокартах. Технология OpenCL. Часть 2. Алгоритмы в условиях массового параллелизма05.05.2022 17:31

Автор курса «Разработчик C++» в Яндекс.Практикуме Георгий Осипов провёл вебинар «Вычисляем на видеокартах. Технология OpenCL».

Мы подготовили для вас его текстовую версию, для удобства разбив её на смысловые блоки.
1. Зачем мы здесь собрались. Краткая история GPGPU.
1a. Как работает OpenCL.
1b. Пишем для OpenCL.
2. Алгоритмы в условиях массового параллелизма.
Не каждый алгоритм ложится на модель массового параллелизма. Возьмём, к примеру, сортировку. Существуют десятки алгоритмов сортировки, но как применить к ним специфику массового параллелизма, совсем не очевидно. Проблема в том, что положение каждого элемента будет зависеть от глобальных особенностей массива, который вы сортируете. А при массовом параллелизме необходимо иметь способ обрабатывать элементы независимо. Но подходящие алгоритмы сортировки всё-таки существуют. Подробно узнать о них можно в курсе Николая Полярного, на который я уже не один раз ссылался в этой серии постов. А мы рассмотрим два более простых алгоритма.

Суммирование чисел — так ли это просто?

Давайте попробуем решить задачу на первый взгляд совсем простую: просуммируем набор чисел. Допустим, что массив уже лежит в видеопамяти и его не надо гонять по медленной шине. Ситуация довольно частая: ваш алгоритм вычислил ряд характеристик, но сами они вам не нужны, интересует лишь сумма. Эту задачу ещё называют редукцией.
Первое, что приходит на ум, — пройтись циклом по всем числам и просуммировать их, используя переменную-аккумулятор. Так же, как это делается на CPU:

__kernel void do_sum(
    __global const float* numbers, __global float* result, int w) {
    *result = 0;
    for (int i = 0; i < w; ++i) {
        *result += numbers[i];
    }
}

Видите, где ошибка?

Kernel — это программа для одного робота — work item’а. Каждый из них будет выполнять эту функцию. То есть целая стая work item’ов накинется суммировать все числа. Работа будет выполнена многократно. Это явно не то, чего мы желаем добиться.

Пусть лучше work item отвечает за прибавление одного числа: kernel получает свою позицию в массиве, то есть он знает, какой float нужно прибавить, и прибавляет его.

А почему неправильно сейчас, догадались?

В такой программе неизбежно возникнет гонка. Гонка — это понятие асинхронного программирования, ситуация, когда несколько потоков некорректно обращаются к одной и той же ячейке памяти. Причём тут они не только пишут, но ещё и читают — операция += работает в два этапа. Например, есть число 5, мы хотим к нему прибавить 2. Мы прочитали 5, сложили и кладем 7 в ячейку. И в этот же самый момент другой поток тоже прочитал 5 и прибавил 3. Он кладёт 8 одновременно с нашей 7. И всё пропало, ничего не работает.

Поэтому нужна синхронизация. В OpenCL есть средства атомарной синхронизации, но они очень неэффективны, и мы их рассматривать не будем. Вместо этого придумаем кое-что своё.

Во-первых, будем резервировать work item не на каждый элемент массива, а на каждый второй. В этом случае каждый work item сможет на первом шаге просуммировать пару чисел, и эти пары не будут перекрываться.

Если изначально в массиве было 16 элементов, то в задаче будет 8 work item«ов, которые вычислят 8 сумм. Далее разбиваем 8 сумм на 4 пары и складываем их четырьмя work item’ами. При этом другие четыре work item’а будут спать. На следующем этапе поработают только два work item’а, сделав из четырёх сумм две. Окончательный результат этой операции получит последний work item, который будет трудиться в одиночку.

Но остаётся открытым вопрос: куда наши роботы — work item’ы будут сохранять промежуточные результаты вычисления? Алгоритм таков, что результаты, полученные одним work item’ом, должны быть обработаны в другом. Например, последний поток должен сложить два числа: полученное им самим на предыдущем шаге и ещё какое-то. Если сохранять в переменную, то work item не сможет получить значение этой же переменной у другого work item. Здесь возникает необходимость в локальной памяти. Подошла бы и глобальная, но её эффективность значительно ниже.

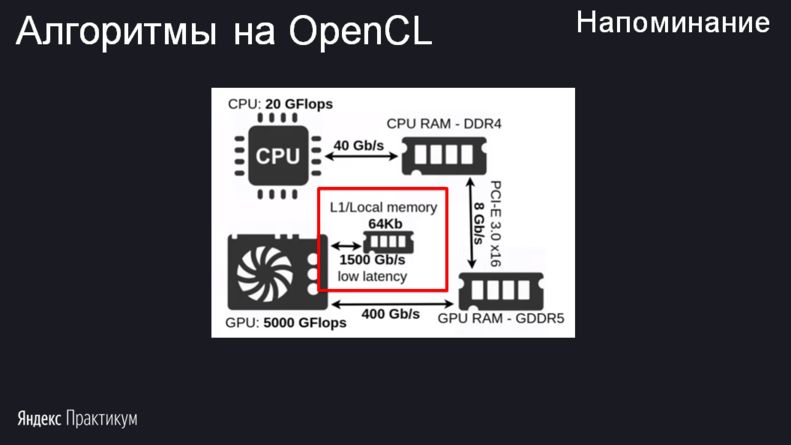
Изображение из compscicenter.ru/courses/video_cards_computation

Когда каждый work item сложил два числа, он должен поместить сумму в локальную память, и далее брать данные из этой памяти может любой другой work item той же рабочей группы.

Но сразу возникает другая проблема. Локальная память существует только в контексте одной рабочей группы. И просуммировать весь массив, разбитый на несколько рабочих групп, не получится. Мы сможем просуммировать числа в каждой рабочей группе. А дальше есть выбор:

выгрузить эти данные на CPU и досуммировать всё уже на нём,
еще раз запустить kernel, и если всё влезает в одну рабочую группу — завершить суммирование. А если не влезает, то просуммировать то, что влезло, а затем ещё раз вызвать kernel. И так до тех пор, пока не получится уместить всё в одну рабочую группу.

При реализации алгоритма сперва сложим два числа v1 и v2 из исходного массива in_data, располагающегося в глобальной памяти. При этом нужно убедиться, что числа находятся в диапазоне массива. Результат сохраним в локальную память, и далее к массиву in_data обращаться уже не понадобится — все необходимые данные перешли в локальную память:

__kernel void reduction(int length, 
    __global const float* in_data, __global float* out_data)  {
    // lid от local id - координата work item в текущей рабочей группе.
    // gid от global id - координата work item во всей задаче.
    int lid = get_local_id(0), gid = get_global_id(0);
    int group_size = get_local_size(0);

    float v1 = gid * 2 < length ? in_data[gid * 2] : 0;
    float v2 = gid * 2 + 1 < length ? in_data[gid * 2 + 1] : 0;

    // Локальная память
    __local float partial_sums[256];
    partial_sums[lid] = v1 + v2;

		...
}

Далее нужно досуммировать все значения рабочей группы и сохранить результат в глобальную память:

Посмотрим на главный суммирующий цикл. В нём есть if, который определяет, какие work item’ы работают, а какие ждут своей очереди. На первой итерации работают чётные work item«ы, на второй — кратные четырём и так далее. В конце только первый work item записывает итоговый ответ.

Этот алгоритм уже близок к истине, но всё равно работает неверно. Не факт, что наши роботы — work item«ы идут синхронно. Даже если они находятся внутри одной рабочей группы, потоки разных ворпов выполняются асинхронно. В результате может возникнуть ситуация, что один поток берёт результат другого потока с предыдущего этапа, а тот его ещё не закончил. Нужно убедиться, чтобы поток не начинал следующий этап до того, как все остальные закончат предыдущий. К счастью, в OpenCL есть средства синхронизации потоков одной рабочей группы. И они гораздо эффективнее, чем средства атомарной синхронизации. Выполняют эту задачу барьеры:

Функция barrier позволяет сделать так, чтобы work item ждал, пока все остальные потоки его рабочей группы дойдут до этой строчки. Он доходит до барьера, и, если ещё не все роботы до него дошли, ждёт. Барьер — очень эффективный инструмент синхронизации.

Барьер мы поставили не только после первого суммирования, но и внутри цикла. Это пришлось сделать, поскольку work item«ы на каждой итерации должны получить результаты других work item«ов. А значит — дождаться завершения этих операций. За это и отвечает барьер. Таким образом, будет несколько синхронизаций.

У читателя может возникнуть вопрос: средства синхронизации всё равно требуют вычислений. Почему бы не поместить барьер внутрь if вот так:

for(int i = 2; i <= group_size; i <<= 1) {
    if(lid % i == 0) {
        partial_sums[lid] += partial_sums[lid + (i >> 1)];
        barrier(CLK_LOCAL_MEM_FENCE);
    }
}

Это было бы логично, но неверно. Смысл барьера в том, что до него должны дойти все потоки рабочей группы. А если барьер внутри if, то часть потоков не дойдёт до него никогда, а другие будут ждать вечно.

Ещё обратите внимание на локальную память. Мы использовали магическое число 256 для массива в локальной памяти — ни больше, ни меньше. Этот алгоритм редукции можно вызывать только с рабочими группами размера 256.

Остался нераскрытым вот какой вопрос: как поступить, если вы хотите написать универсальную редукцию, которая будет работать с группами любого размера? Массивов переменной длины и тем более динамических в OpenCL нет, так что наивный подход, состоящий в замене магического числа 256 на вычисляемое значение, не сработает. Можно поступить иначе — вычислить нужный размер массива на CPU и передать сам массив локальной памяти как аргумент при вызове kernel.

Можно ли лучше? Куда оптимизировать

С четвёртой попытки, наконец, написан верный алгоритм суммирования, но так ли он хорош? Ответ: хорош, но можно лучше. Для этого нужно учесть особенности работы с кешами, локальной памятью. Технологии, применяемые в видеокартах для оптимизации, довольно сложны. Останавливаться не будем, подробности есть в лекциях Николая Полярного.

Также для ускорения можно использовать векторные типы — заменить float на float4, float8 или даже float16. Не факт, что это поможет — здесь и так уже массовый параллелизм. На определённых картах это может дать выигрыш, но на большинстве — нет.

Ещё один способ оптимизации — запуск нескольких kernel параллельно. Host-код в состоянии накидать на видеокарту сразу с десяток kernel, не дожидаясь, пока завершится каждый предыдущий. По моим бенчмаркам это даёт очень неплохое ускорение. Не факт, что вы написали идеальный kernel, оптимально загружающий видеокарту. А значит, видеокарта сможет параллельно исполнять несколько задач, чтобы задействовать все свои ресурсы. Видеокарта умная: если ей дать много заданий, она сама решит, как их нужно исполнять, в каком порядке распараллеливать, чтобы достичь большей эффективности.

Все хост-функции OpenCL (кроме clSetKernelArg) — потокобезопасные. Можно смело брать несколько тредов, и из них посылать вычисления на видеокарту. Ещё я заметил, что есть смысл в каждом треде выделить свой контекст. Не знаю, чем это обусловлено, но почему-то производительность при таком подходе возрастает. Думаю, видеокарта знает, что буфер одного контекста никак не зависит от буферов другого контекста. Возможно, за счёт этого видеокарта может более гибко их параллелить. Но учтите: если в одном контексте выделить буфер, то kernel другого контекста не сможет с ним взаимодействовать.

Сворачиваем с умом. Перекрывающиеся группы

Ещё один несложный алгоритм, который мы разберём, — это свёртка изображений. Алгоритм очень часто используется в машинном обучении и имеет массу других применений. Одно из них — Гауссово размытие.

Коэффициенты, на которые умножается изображение, называются ядром. Будем использовать для него слово kernel, надеясь, что не возникнет путаницы с понятием kernel-код. Если решать задачу в лоб, то получится такая программа:

// Получаем координату целевой точки.
const int2 p = (int2)(get_global_id(0), get_global_id(1));

// Сохраняем границы нашего изображения в переменные для удобства.
const int2 top_left = (int2)(0, 0);
const int2 bottom_right = (int2)(w - 1, h - 1);

float acc = 0;

// Считаем, что размер ядра kernel — это 2 * RADIUS + 1,
// а переменная kernel указывает на серединный пиксель.
for (int y = -RADIUS; y < RADIUS; ++y) {
    for (int x = -RADIUS; x < RADIUS; ++x) {
        int2 offset = (int2)(x, y);

        // Приводим точку (p + offset) к границам изображения.
        int2 src_pt = min(bottom_right, max(top_left, p + offset));
        
        // Умножаем элемент kernel на элемент изображения и
        // прибавляем к аккумулятору
        acc += kernel[x + y * kernel_stride] * src[src_pt.x + src_pt.y * src_stride];
    }
}

// Будем присваивать ответ, только если целевой пиксель попал в границы 
// изображения. Иначе возможен выход за пределы буфера.
if (all(p <= bottom_right)) {
    dst[p.x + p.y * dst_stride] = acc;
}

Обратите внимание, что под if мы поместили только сам код записи. Получается, что для пикселей, вышедших за границы, сделаем лишние вычисления. Но ничего плохого в этом нет: за границы выйдет не так много пикселей, и многие из них всё равно были бы фиктивно посчитаны из-за дивергенции.

Можно было бы поднять if выше, помещая в него весь большой цикл. Это сработает лишь потому, что в том коде нет барьеров. А значит, лучше не рисковать и не экономить граничные пиксели — вдруг однажды понадобится усложнить код, добавив барьеры в цикл, или какую-нибудь из вызываемых им функций. Тогда легко забыть про if и получить ошибку.

Этот алгоритм довольно ресурсоёмкий, ведь для каждого пикселя исходного изображения нужно обсчитывать целый квадрат. Вычисления можно существенно ускорить, если ядро свёртки $K$ разложимо, иначе говоря, $K_{ij} = A_i\cdot B_j$ . В случае размытия по Гауссу имеет место даже более сильная разложимость: $K_{ij} = A_i\cdot A_j$ . Такое ядро напоминает таблицу умножения:

Чтобы получить элемент ядра, нужно умножить число сверху от столбца на число слева от строки. На иллюстрации элементы ядра округлены. Свёртка таким ядром позволяет неплохо сократить количество вычислений. Для этого будем отдельно сворачивать столбцы, а затем результаты этих свёрток сворачивать по строкам:

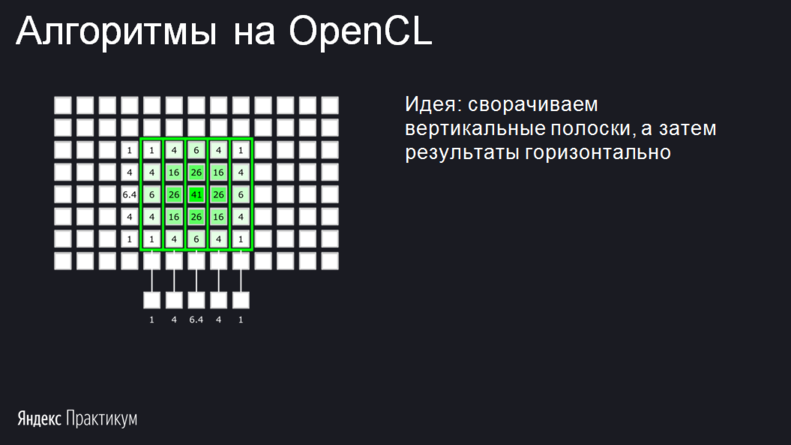
Профит в том, что результаты свёртки столбцов можно запомнить и затем использовать для вычисления двух соседних пикселей с каждой стороны. Запоминать будем, естественно, в локальную память.

На слайде приведён псевдокод этого алгоритма. Реализация остаётся в качестве упражнения:

Чтобы всё заработало, нужно ответить ещё на один вопрос: откуда крайние слева и справа work item«ы в каждой рабочей группе будут брать данные? Они рассчитывают получить их от соседних потоков, а тех может не быть. Можно посчитать дополнительные свёртки в if, но если вы усвоили понятие дивергенции, то знаете, что это не лучшая идея. Гораздо эффективнее было бы добавить в рабочую группу фиктивные work item«ы. Эти потоки не должны записывать результат в финальный буфер, их задача выполнить код только до барьера — посчитать вертикальные свёртки столбцов, которые потом будут использованы в других work item«ах.

Если следовать этому подходу, то рабочие группы нужно создавать с перекрытиями:

В примере на слайде размер ядра равен пяти. Два крайних столбца с каждой стороны рабочей группе не вычисляют значений. Получается, что перекрытие должно составлять 4 пикселя. Для самой левой и самой правой рабочей группы фиктивные пиксели можно не добавлять. Результат в них дублирует результат крайнего столбца.

Но при реализации этого алгоритма возникнет проблема. OpenCL не знает ни про какие перекрытия — для него все рабочие группы располагаются друг за другом. Вычисление реального размера задачи и положения пикселя, за который отвечает work item, становится вашей заботой. В такой задаче вам не поможет get_global_id, лучше обращаться к номеру рабочей группы и пикселя в ней.

Может возникнуть вопрос: что, если изменить порядок свёртки: вначале сворачивать строки, а потом столбцы? Тогда рабочие группы будут перекрываться не по горизонтали, а по вертикали. Результат не изменится, но при таком подходе будет гораздо менее эффективно работать кэш. В результате скорость вычислений может упасть в 10 и более раз. Так лучше не делать.

Напоследок разберём, насколько увеличится размер задачи за счёт перекрытий. Нетрудно заметить, что для минимизации площади перекрытий лучше выбирать как можно более вытянутые по горизонтали рабочие группы. Тогда перекрытия будут составлять меньший процент от них. В идеале — горизонтальные полоски. Если предположить, что максимальная площадь рабочей группы — 256 пикселей, то при таком раскладе перекрытия составят примерно 1,6%. В этой задаче для минимизации перекрытий можно попробовать использовать максимальный размер рабочей группы, а не заданный магическим числом.