RESHI.RU — робот решает и объясняет школьные текстовые задачи по математике08.10.2019 23:33

Введение

Когда я объяснял своему ребёнку в 4-м классе, как решать текстовую задачку по математике, то неожиданно понял две вещи. Во-первых, процесс объяснения решения можно автоматизировать. А во-вторых, для большинства школьных вычислительных задач подходит универсальный метод через систему уравнений, который почему-то пока не изучается в младших классах школы. Причём освоение этого метода вполне по силам среднему школьнику и позволит справляться с ранее недоступными ему задачами. Результатом этого понимания явился сайт RESHI.RU с объясняющим задачи роботом.
Отличием от многочисленных сайтов с готовыми домашними заданиями является то, что задача может быть решена теоретически любая, а не заранее заданная. Но только теоретически, поскольку практически робот понимает только те типы задач, для которых сделана программная реализация. На задачах учебников за 4-й класс робот показывает 65% правильных решений (а если не может или сомневается, то честно об этом предупреждает), за 3-й класс — около 80%.
Решаемая задача должна быть сформулирована текстом без ошибок, не иметь графической информации в условии (картинки, схемы) и быть вычислительной, то есть ответом должны получиться одна или несколько величин. Величины в условии задачи могут быть как числами, так и переменными.

Робот пытается составить для задачи систему из простых уравнений и решить её. Для некоторых типов задач робот может решить и школьным способом, который предлагается как дополнительный.

И всё-таки у RESHI.RU основной целью является не решение конкретных задач, а объяснение на примерах универсального метода решения через систему простых уравнений.

Пример задачи

Рассмотрим пример решения роботом следующей задачи с сайта RESHI.RU.

Из поселка и города навстречу друг другу, одновременно выехали два автобуса. Один автобус до встречи проехал 100 км со скоростью 25 км/час. Сколько километров до встречи проехал второй автобус, если его скорость 50 км/час.

Робот понял, что это задача на движение двух объектов и он умеет такие решать. Осталось
правильно выделить все величины, понять их типы и соотнести с этими двумя объектами.
В качестве объяснения робот выводит последовательность разделов, в каждом из которых описывается тот или иной аспект, приближающий к получению ответа. Приведём здесь скриншоты этих разделов.

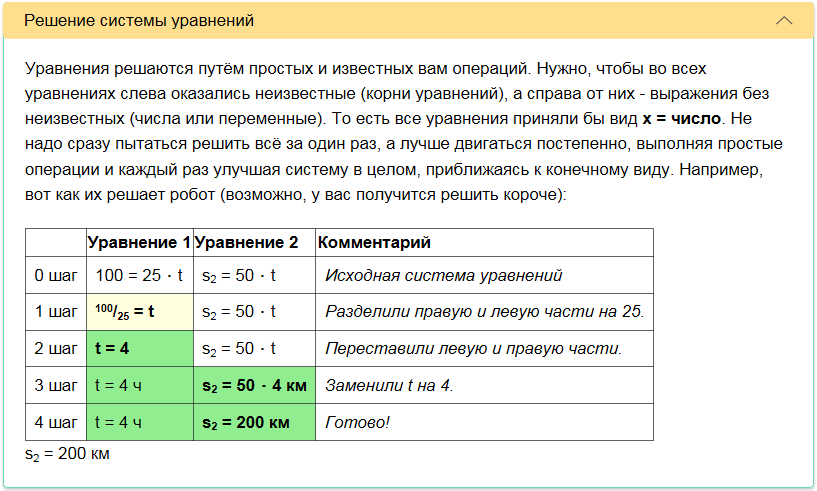
Робот также понял, что помимо универсального способа есть и школьный способ решения, который короче и проще.

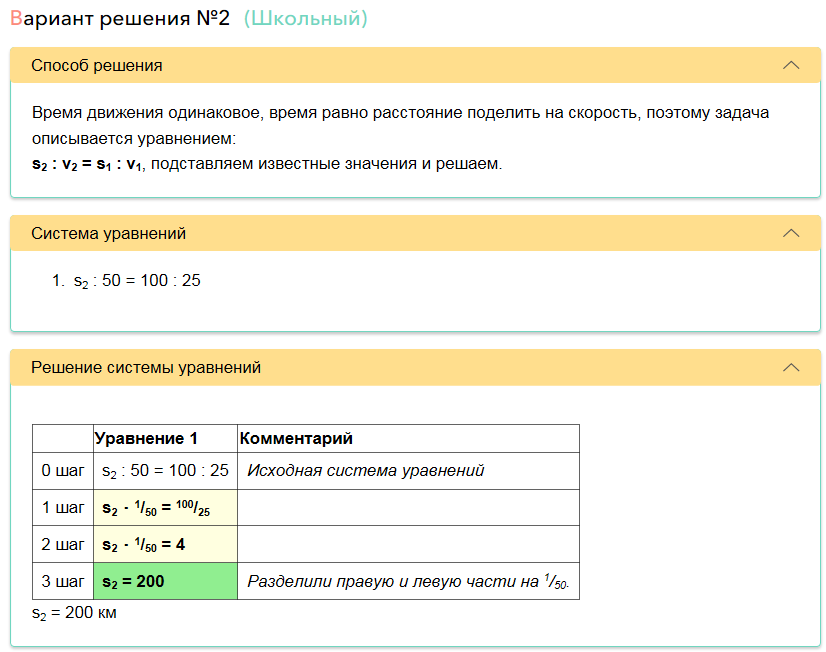
Всё это вместе со схемой генерируется автоматически для каждой решаемой задачи, а не задано изначально.

Универсальный способ решения

Большинство школьных текстовых задач можно решить универсальным методом — через систему простых уравнений. Если ученик освоит этот метод, то он в принципе сможет решить любую типовую школьную задачу по математике, заданную текстом.

В 1-м классе школьников учат решать простые задачи, описываемые одним уравнением a = b + c или a = b — c. А в 3-м классе после освоения операций умножения с делением появляются простые задачи на a = b ⋅ с или a = b / c. Составные задачи — это те задачи, которые не являются простыми, то есть не описываемые одним уравнением с тремя величинами. Здесь ученику предлагается проявить смекалку, чтобы либо составить одно сложное уравнение, либо свести задачу к ряду более простых задач, решающихся одна за другой. Составные задачи со сложением и вычитанием активно предлагаются со 2-го класса, а с 3-го класса сложность ещё возрастает с появлением новых операций.

Но есть ещё один способ решения составных задач, и состоит он в том, чтобы составить несколько простых уравнений (систему уравнений), а затем решить её целиком. Действительно, если ученик может решать простые задачи (то есть правильно составлять простое уравнение по тексту условия), то для составной задачи он в принципе может составить для каждого отдельного условия своё простое уравнение. Для этого нужно все встречающиеся величины обозначать своими символами (например, x, y, z, …), и формировать для них соответствующие x = y + z и т.д. Потом подставить конкретные числа в уравнения. А затем решить эту систему, последовательно определяя неизвестные значения.

Данный способ может оказаться более трудоёмким для решения на конкретной задаче, так как некоторая «изюминка» обычно упрощает работу. Но её не всегда можно обнаружить, так как это своего рода искусство. А универсальный метод не требует этого, являясь технологией типа «делай раз, затем делай два, а вот и ответ».

Робот пользуется именно универсальным способом и старается максимально подробно объяснить на конкретной задаче, как он получает решение. Предполагается, что ученик потратит некоторое время на понимание того, как это делает робот, чтобы в дальнейшем повторять подобные действия на других задачах. Однако робот предлагает и школьный вариант решения, если для этого типа задач робот ему обучен (сейчас не для всех типов, но постепенно обучится).

Полезно это или нет для учеников — вопрос спорный. С одной стороны, это может повысить процент решаемых учениками задач. С другой стороны, в некоторых из учеников такая технологичность может подавить нежные ростки математической смекалки. Предлагаю направлять автору или записывать здесь свои обоснованные соображения и опасения.

Классификатор задач

По системе простых уравнений задачи можно автоматически расклассифицировать. Это может пригодиться, например, для того, чтобы предложить ученику решить аналогичную задачку для закрепления навыка. Также робот может понять, к какому реально классу относится задача, ибо даже в учебниках 4-го класса попадаются задачки уровня 1-го класса!

В настоящий момент на сайте загружено более 4000 задач из реальных учебников, и можно увидеть этот автоматический классификатор на этих задачах.

Реализация робота

Разумеется, возникает резонный вопрос —, а как это робот делает? Сразу скажу, что это очень сложная реализация. Я занимаюсь обработкой текстов естественного языка около 10 лет, и это — самая сложная задача из тех, которые мне встречались в этой области. Сложность состоит в том, что нужно правильно выделить числовые величины, понять их тип и связать с объектами. Любая неточность хотя бы в одном из аспектов приводит к неправильному результату.
Перечислю только некоторые из проблем, с которыми пришлось столкнуться.

Псевдо-величины, которые не относятся к задаче (На кусте было 2 распустившиеся розы. Через 3 дня распустилось еще 4 розы. Сколько роз на кусте?);
Неявные величины, задаваемые разными комбинациями типа «столько же», «половину от» и прочее;
Синонимия, когда один и тот же объект обозначается разными комбинациями (грузовой автомобиль = грузовик);
Сложность с идентификацией объектов (От двух пристаней навстречу друг другу отплыли теплоходы… — непонятно, кто здесь объекты, пристани или теплоходы?);
Анафора (местоимения он, она, оно) не всегда однозначно ссылаются на объект;
Необходимость расщеплять задачу на подзадачи, когда базовое условие одно, но дополнительные условия или что нужно найти вариативны;
Неявное условие, кардинально меняющее смысл задачи (Крышка стола имеет 3 угла. Один угол спилили. Сколько углов стало у крышки стола?);

Но это то, что лежит на поверхности. На алгоритмическом уровне этих проблем гораздо больше.
Основная идея алгоритма состоит в том, что реализуются специфические обработчики задач, понимающие свои типы. Задача прогоняется по всем обработчикам, и какой распознает свой тип, тот и решает задачу. Каждый обработчик решает довольно широкий спектр задач своего типа.

Сейчас эти типы такие:

Задачи на движение одного или нескольких объектов;
Задачи на прямоугольники и квадраты (один или несколько), площади, периметры, заполнение одних другими;
Задачи на однородные величины (когда все величины сводятся к одной размерности, а сама задача — к системе линейных уравнений);
Задачи на двуродные величины (когда присутствует умножение в системе уравнений);
Явно описывающие уравнение (например, Частное чисел 2082 и 6 равно сумме задуманного числа и числа 48);
Задачи на время суток;
Задачи на среднее, преобразование размерностей и др. мелочи;

Когда робот понял задачу, то есть отнёс её к одному из поддерживаемых типов, правильно расставив величины и поняв, что нужно вычислить, он может сгенерировать своё понимание своим языком. Кстати, на сайте это понимание выводится справа от текстов задач для учебников. Приведём примеры с сайта.

Условие: Частное чисел 2082 и 6 равно сумме задуманного числа и числа 48.
Понимание: Найти корень уравнения: 2082: 6 = x + 48.

Условие: Спектакль для детей начался в 11 ч и закончился в 12 ч 35 мин. Сколько времени длился этот спектакль?
Понимание: Есть временной интервал. Начало интервала 11 ч. Окончание интервала 12 ч 35 мин. Какова продолжительность интервала?

Условие: Ане 12 лет. Она в 3 раза старше брата. На сколько лет Аня старше брата?
Понимание: Есть 2 числовые величины: возраст Ани и возраст брата. Возраст Ани равен 12, он в 3 раза больше, чем возраст брата. На сколько возраст Ани больше, чем возраст брата?

Условие: Один токарь каждый час изготавливает 8 деталей, а другой — 7 деталей. За сколько часов они изготовят вместе 90 деталей, если выработка в час у них не изменится?
Понимание: Есть 2 объекта: токарь №1 и токарь №2. Число деталей в ч токаря №1: 8 деталей. Число деталей в ч токаря №2: 7 деталей. Суммарное число деталей совместно: 90 деталей. Время у всех объектов одинаково. Какое значение в ч имеет время?

Условие: Из двух сёл одновременно навстречу друг другу вышли два товарища — Миша и Коля. Миша шёл со скоростью 3 км/ч, а Коля — 5 км/ч. Одновременно с Мишей к Коле побежала собака. Она бежала со скоростью 8 км/ч. Добежав до Коли, она повернула назад, к Мише, и так и бегала между ребятами, пока они не встретились. Сколько километров пробежала собака, если расстояние между сёлами 16 км?
Понимание: Два объекта (миша и коля) одновременно начали движение друг к другу с расстояния 16 км. Между ними перемещается туда и обратно 3-й объект (собака) со скоростью 8 км/ч. Первый объект (миша) перемещался со скоростью 3 км/ч. Второй объект (коля) перемещался со скоростью 5 км/ч. Какой путь в км преодолел 3-й объект?

Условие: В комнате, длина которой 8 м, а ширина на 2 м меньше длины, надо покрасить пол. Сколько для этого понадобится краски, если расходовать по 150 г на 1 м²?
Понимание: Прямоугольник длиной 8 м. Ширина на 2 м меньше, чем длина. Площадь заполняется элементами по 150 гр на единицу площади. Сколько элементов на всю площадь?

Что дальше?

Планируются следующие направления развития:

Повысить процент решаемых задач. Сейчас для задач 4-го класса робот показывает 65% правильных решений, для 3-го класса — около 80%, для 1 и 2 — процент ещё выше;
Организовать продвижение сайта;
Ввести задачи всех популярных учебников по математике, в том числе и для стран СНГ (на русском языке);
Поддержать другие языки славянской группы;
Пойти в направлении 5-го класса и далее;
Подумать о текстовых задачах по физике;

Реализация этих направлений будет зависеть от реальной востребованности сайта.