Математические фантазии о справедливости25.03.2024 17:01

Почему каждый раз, когда люди пытаются построить рай на Земле, это заканчивается адом? И температура этого ада тем выше, чем ярче пылают сердца в праведном порыве осчастливить мир.

Может быть, строили не так, или может быть, общество еще не доросло до нового миропорядка, но при достижении определенного уровня технологического развития и гуманитарного знания мы сможем воплотить мечту поколений в реальность?

Или может быть, есть объективные причины невозможности рая на Земле, и все как раз наоборот, и мы движемся не к светлому будущему, а к антиутопии с жесточайшей диктатурой и дичайшим социальным расслоением?

Или же истина, как обычно, где-то посередине, но тогда к какому краю ближе?

Я попытался порассуждать, или даже скорее пофантазировать, на эту тему на языке математики. Мне показалось интересным, что в этой в принципе гуманитарной теме математика дает адекватные результаты. Приятным бонусом для меня явилось то, что так любимый всеми физиками принцип наименьшего действия смотрится здесь вполне гармонично. В рамках построенной нами математической модели мы получим уравнения, хорошо знакомые из курса теоретической механики, что для меня стало несколько неожиданной иллюстрацией универсальности математических законов.

Постановка задачи

В самом общем виде, наша задача заключается в построении элементарной математической модели распределения благ среди людей и исследовании нескольких простейших сценариев.

Мы увидим, что даже эта элементарная модель позволит нам сделать некоторые выводы.

Энергия

Обозначим все блага, которые потребляет человечество в единицу времени (для определенности возьмем месяц), через E_0 . Чтобы избежать неоднозначности, мы будем рассматривать все блага, как материальные, так и «духовные». Все, что может быть полезно человеку, доставить ему удовольствие и что можно продать ему как товар (даже чисто теоретически) — все это входит в E_0 . Все это мы будем называть энергией.

Комментраий. Определение может показаться неясным, но это не станет препятствием для нашего дальнейшего анализа, потому что единственное свойство, которое нас будет интересовать, - это конечность этой энергии. В разные моменты истории человечества в силу технологического и культурного развития и природных факторов эта энергиябыла разной, но все же она всегда конечна.

Эта энергия как-то распределяется между людьми. Потребление благ отдельно взятым человеком в нашу условную единицу времени мы будем называть обобщенным доходом или просто доходом данного человека, и, конечно, доход явно влияет на его физическое и «душевное состояние», которое мы упростим до одномерной шкалы удовольствие-страдание. При снижении уровня доступных благ человек начинает страдать, в то время как повышение данной энергии приносит удовольствие.

Функция распределения энергии между людьми

Проранжируем людей по доходу.

Теперь будем пересчитывать людей, начиная с самых бедных и двигаясь к богатым. Для простоты предположим, что доход двух различных людей всегда, хотя бы немного, но отличается. Для каждого -го человека посчитаем суммарную энергию e(n) , потребляемую всеми подсчитанными () людьми — всеми, кто беднее него, плюс он сам.

e(n)

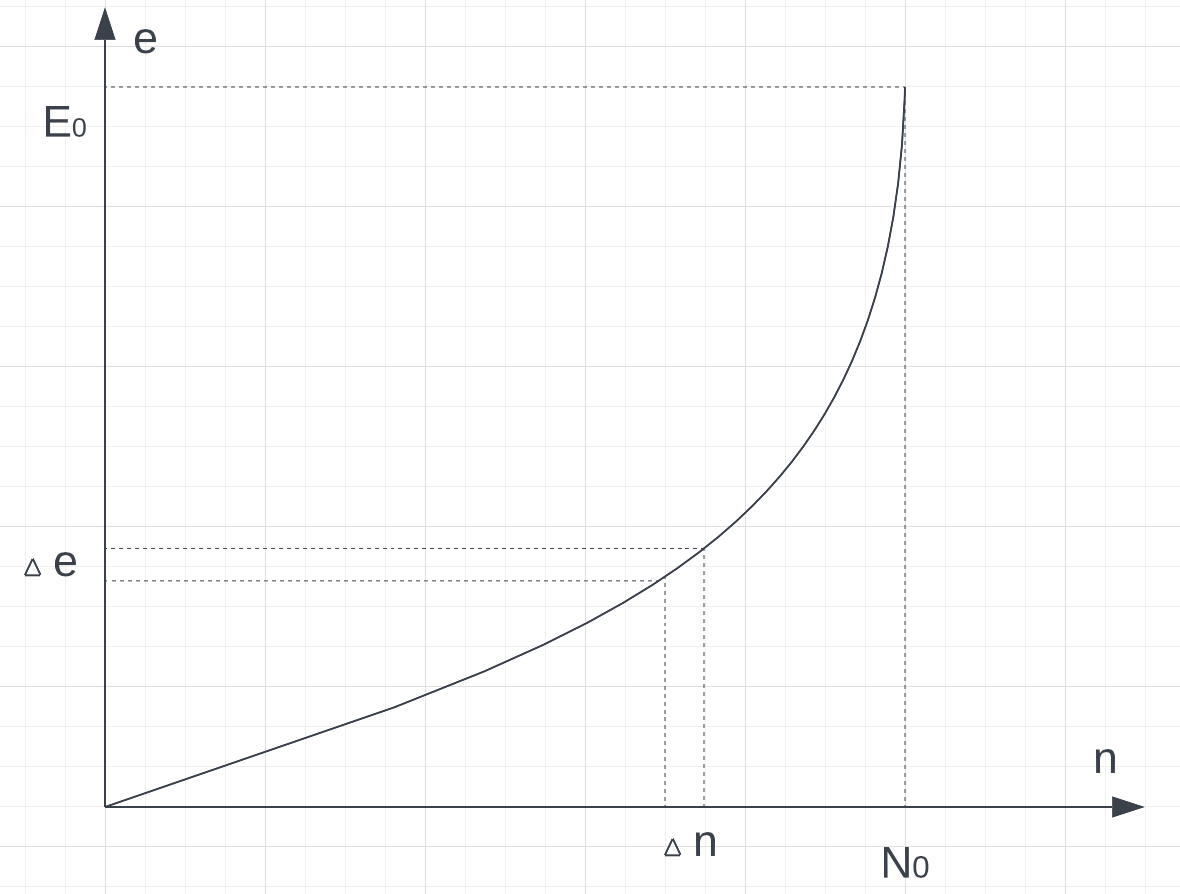
e (n)

График e(n) будет выглядеть как-то так.

Возьмем произвольную группу людей $\Delta n << N_0$ с максимально близким доходом. Понятно, что $\displaystyle \frac{\Delta e}{\Delta n}$ есть количество энергии, потребляемое одним человеком в группе $\Delta n$ .

Перейдем к безразмерным координатам:

$e -> \displaystyle \frac {e}{E_0}» src=«https://habrastorage.org/getpro/habr/upload_files/9f8/330/795/9f8330795d5b49094827bc97ca445e32.svg» />, <img alt=$ \displaystyle \frac {n}{N_0}» src=«https://habrastorage.org/getpro/habr/upload_files/77d/2d2/10a/77d2d210a35d8b1ee6982b3b055a78f9.svg» />

x(y)

x (y)

Комментарий: Ось абсцисс я обозначил через , а ось ординат через . Я сделал это намеренно, потому что через абзац мы перейдем к обратной функции и дальше будем работать только с ней.

Т.к. N_0 очень большое, мы можем перейти к континуальной .

Тогда x'(y) c точностью до коэффициента E_0/N_0 является энергией потребляемой одним человеком.

Нам будет удобно работать с обратной функцией, которая будет выглядеть как-то так:

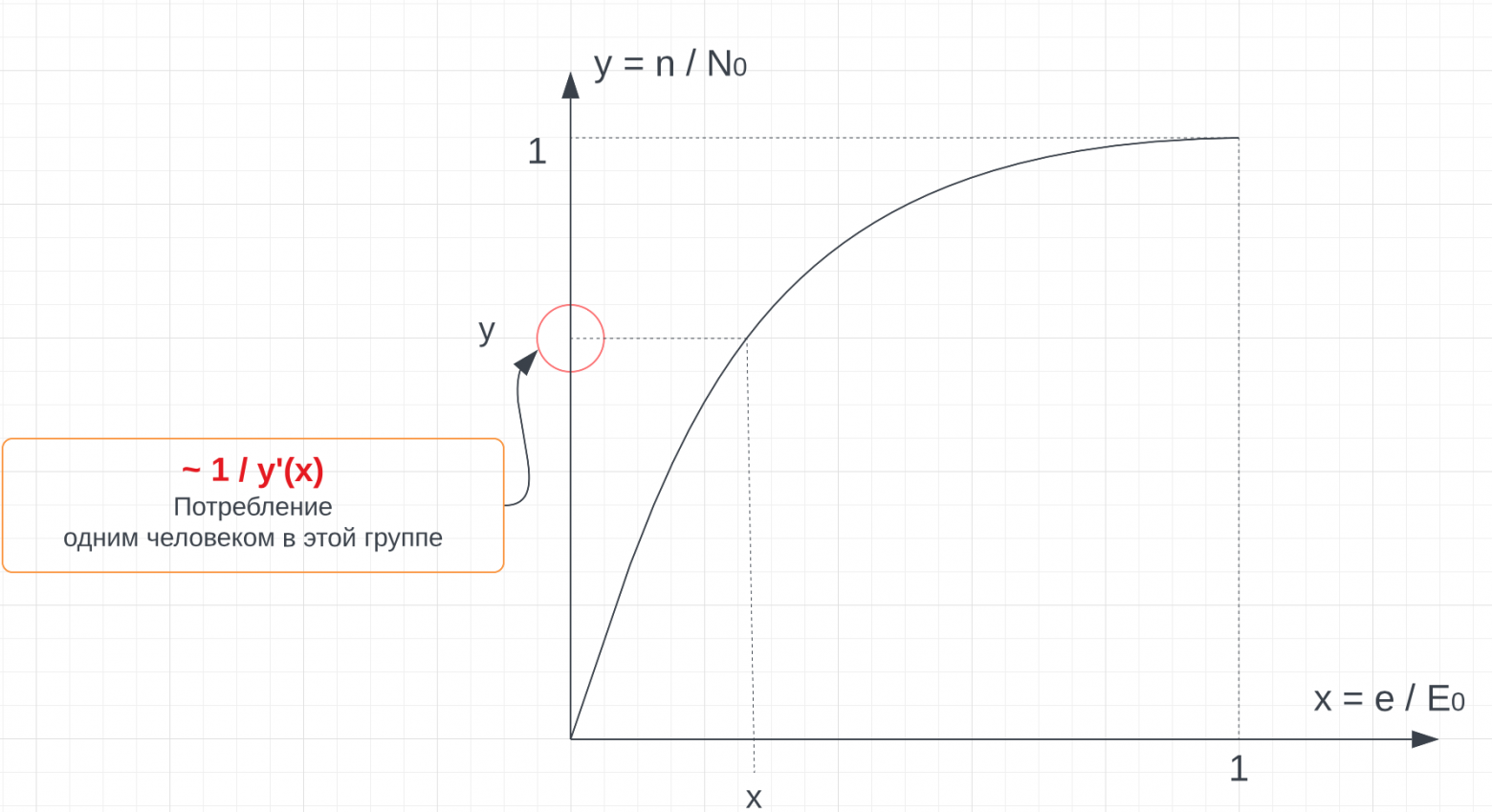
Тогда E_0/(y'(x)N_0) является доходом человека в группе, соответствующей .

В дальнейшем все расчеты мы будем проводить с этой функцией y(x) . Вот некоторые свойства этой функции:

Функцию, удовлетворяющую этим условиям, будем называть допустимой функцией распределения.

Функция страдания-удовольствия, элементарный случай

Понятно, что, если человек получает слишком мало энергии, то он страдает. Чем больше человек получает энергии, тем меньше он страдает. Введем функцию $\xi(x)$ , которая представляет страдание отдельного человека в группе людей окрестности . В рамках нашей модели, давайте для простоты примем, что страдание обратно пропорционально доходу, что значит, что наша функция будет прямо пропорциональна y'(x) :

$\xi (x) = A y'(x)$

Так как позже мы добавим слагаемые, связанные с удовольствием (они будут отрицательными), то мы будем называть функцию $\xi (x)$ функцией страдания-удовольствия.

Лагранжиан страдания-удовольствия, элементарный случай

Давайте найдем суммарное страдание всего человечества, связанное с нехваткой энергии. Обозначим эту величину через . Тогда

$S = \displaystyle \int_0^1 \xi(x)dy = \int_0^1 \xi(x)y'(x)dx = A\displaystyle \int_0^1 y'^2(x)dx$

А теперь сформулируем гипотезу. Предположим, что человечество, как единый организм, всегда пытается минимизировать общее страдание . Это значит, что функция распределения энергии y(x) автоматически «поднастраивается» таким образом, чтобы минимизировать .

Тогда мы получаем классическую задачу вариационного исчисления с лагранжианом:

L = Ay'^2(x)

Комментарий: В рамках классической механики этот случай аналогичен случаю свободного движения материальной точки в одномерном пространстве. Лагранжиан в этом случае является просто кинетической энергией материальной точки с массой :

$L = \displaystyle \frac {m^2}{2}x'^2(t)$

С учетом краевых условий достигает минимума для функции

y(x) = x

Эта функция является допустимой функцией распределения (удовлетворяет всем требованиям, которые мы предъявляем к этой функции). При этом доход любого человека:

$\displaystyle \frac {E_0} {N_0}$

Прекрасный, справедливый мир.

Это элементарная задача из классической механики с известным ответом. Здесь я только хочу напомнить логику рассуждений.

Лагранжиан страдания-удовольствия с удовольствием

Мы уже учли тот факт, что доход влияет на страдание, но мы говорили об объективном, физическом страдании, связанным с нехваткой еды, тепла, … Но было бы разумно предположить, что мы получаем удовольствие пропорциональное нашему доходу. Это что-то не связанное напрямую с нашим выживанием, это просто удовольствие от пользования благами.

Введем новое слагаемое в нашу функцию страдания-удовольсттвия:

$\xi (x) = A y'(x) - B \displaystyle \frac {1}{y'(x)}$

Важно понимать, что A > 0, B>0» src=«https://habrastorage.org/getpro/habr/upload_files/e4a/5ac/621/e4a5ac621abc2a18cb7e60be5d19f080.svg» /> . Знак минус перед <img alt= означает, что этот элемент отвечает за удовольствие.

Тогда

$S = \displaystyle \int_0^1 \xi(x)y'(x)dx = \displaystyle \int_0^1 (Ay'^2(x) - B)dx = A\displaystyle \int_0^1 y'^2(x)dx - B$

Понятно, что этот функционал будет достигать минимума при точно той же функции, что и в предыдущем случае:

y(x) = x

То есть, если мы просто стремимся выжить и просто получаем удовольствие от благ, то это приводит опять к справедливому, равномерному распределению.

Лагранжиан страдания-удовольствия с завистью

Но если мы присмотримся к человеку (и прежде всего к себе) поближе, то мы можем заметить и другие факторы, вызывающие страдание и удовольствие.

Так, наше удовольствие зависит не только от абсолютного количества благ — мы сравниваем свой уровень жизни с уровнем жизни других людей. Нам приятно, когда мы живем лучше других, и мы страдаем, осознавая, что другие живут лучше нас. Эта функция, определяющая наше удовольствие от сравнения себя с другими, может быть довольно сложной. Обозначим ее как f(y(x)) .

С учетом этого нового фактора, наша функция удовольствия-страдания теперь будет выглядеть как

$\xi (x) = A y'(x) - B \displaystyle \frac {f(y(x))}{y'(x)}$

f(0) = 1

Разложим функцию f(y) в ряд Тейлора в точке . Далее, упростим нам задачу и возьмем только постоянную и линейную части разложения. Тогда наша приблизительная упрощенная функция удовольствия-страдания примет вид:

$\xi (x) = A y'(x) - \displaystyle B\frac { 1+ C y(x)}{y'(x)}$

Будем называть коэффициент коэффициентом физического страдания, коэффициент — коэффициентом удовольствия, а коэффициент — коэффициентом зависти.

Здесь важно понимать, что, как и и , коэффициент также положителен (не отрицателен, если быть точным). C > 0» src=«https://habrastorage.org/getpro/habr/upload_files/fa7/5df/913/fa75df9139ef41fb36371aff5803c10a.svg» /> потому что, чем больше людей беднее нас и чем меньше людей богаче нас, тем наше удовольствие больше (страдание меньше).

Тогда полная функция страдания-удовольствия для человечества: 

<img alt=

Лагранжианом является подинтеграьная функция:

L = Ay'(x)^2 - B -BCy(x)

Комментарий. В рамках классической механики это соответствует свободному движению материальной точки в потенциальном поле, где потенциальная энергия пропорциональна (например, высоте):

$s = m\displaystyle \int_0^1\big(\frac {x'(t)^2}{2} - U_0 -gx(t)\big)dt$

Применим критерий Лагранжа-Эйлера:

$\displaystyle \frac{d}{dx}\displaystyle \frac{dL}{dy'} - \frac{dL}{dy} = 0$ 2Ay'' + BC = 0

Обозначим $\alpha = \displaystyle \frac {C}{4A}$

С учетом краевых условий нашим экстремумом является функция:

$y = (1+\alpha)x - \alpha x^2$

Нужно еще доказать, что это минимум, но так как это одна из базовых элементарных задач классической механики, то мы не будем тратить время на это.

На диаграмме представлены графики для $\alpha = 0, \alpha = 0.3, \alpha = 0.6, \alpha = 0.9$

$y'' = -2\alpha$

$y' = 1 + \alpha - 2\alpha x$

С учетом того, что $\alpha$ не отрицательна получаем, что y'' не положительна на всем интервале (0,1) .

будет неотрицательной на всем интервале (0,1) при условии $\alpha \le 1$

То есть для $\alpha \le 1$ мы получаем, что наш минимум является также и допустимой функцией распределения.

Интересно посмотреть на функцию распределения дохода $\displaystyle \frac {1}{y'(x)}$ .

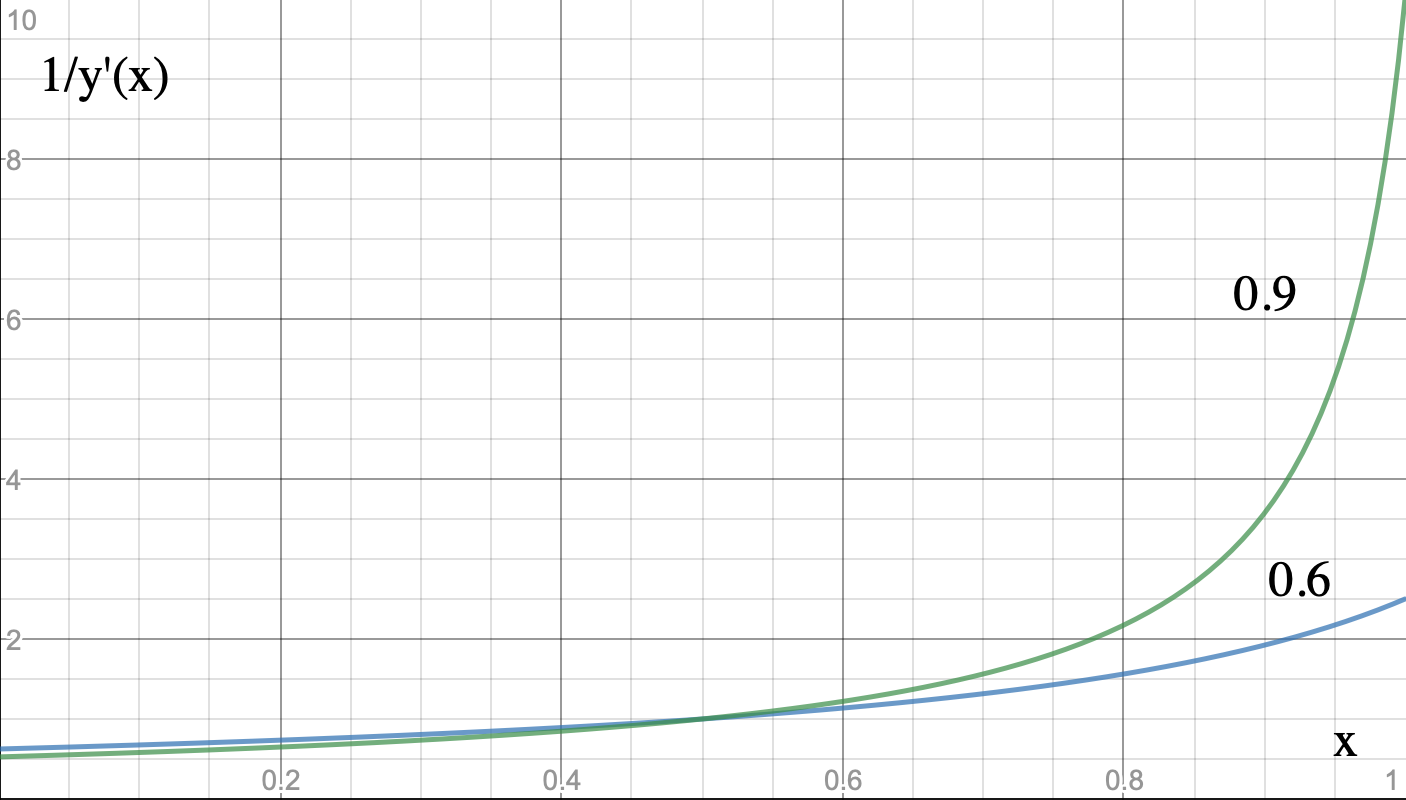
Распределение дохода для $\alpha = 0.9$ и $\alpha = 0.6$

Очевидно, что распределение неравномерно. Это распределение тем более неравномерно, чем больше отношения

$4\alpha = AB/C = (Коэф. Удовольствия) (Коэф. Зависти) / (Коэф. Страдания)$

и в пределе, когда $\alpha= 1$ , мы приходим к крайней форме несправедливого распределения, когда группка самых богатых людей (в левой окрестности x=1 ) получает бесконечно большой доход, что выражается в условии

$y'(x)|_{x=1-} = 0$ (производная берется слева от 1)

Комментарий. Понятно, что это аппроксимация, недостижимая в силу конечности энергии. Этот эффект возникает от того, что мы считаем континуальным, в то время как эта переменная связана с подсчетом людей и конечно же дискретна.

Что делать со значениями $\alpha > 1» src=«https://habrastorage.org/getpro/habr/upload_files/545/944/a6a/545944a6af356792a3a628164e774365.svg» />? При этом значении наш минимум не является допустимой функцией распределения (производная меньше нуля). В этом нет противоречия. Это лишь значит, что локальный экстремум не достижим в классе допустимых функций распределений, и наш искомый минимум будет в точке максимально несправедливого распределения (<img alt=$ ).

Комментарий. Надо заметить, что похоже представляет из себя очень узкий, переходный коридор, и все очень быстро "сваливается" в максимально несправедливого распределения.

Лагранжиан страдания-удовольствия с социальным коэффициентом

Мы видим, что «коэффициент зависти» портит всю картину. Но какова его природа? Если это просто результат воспитания или следствие социальной травмы, страхов, связанных с историческими событиями и передаваемых из поколения в поколение, то это одно. С этим можно работать: это лишь вопрос воспитания, образования и знания.

Но если эта «зависть», это желание жить / быть лучше других, или страх быть хуже заложены в нас на генетическом уровне?

Только сейчас, в развитых странах, мы наконец-то начинаем получать достаточное E_0 , гарантированно обеспечивающее выживание. Наш вид формировался далеко не в условиях рая. Человеку приходилось бороться за выживание с себе подобными, и те, кто были внизу иерархии, часто просто не выживали. Мы можем предположить, что «коэффициент зависти» — это что-то, что было заложено в нас природой в процессе эволюции.

Если это объективный фактор, то можно ли его компенсировать?

Да, с точки зрения нашей модели мы можем компенсировать его введя противоположное «зависти» действие. Это должна быть функция, которая увеличивает страдание, если ты живешь лучше других. Опять-таки, беря постоянный и линейный член в разложении в ряд Тейлора, наша функция страдания-удовольтсвия будет выглядеть следующим образом

$\xi (x) = A y'(x) - \displaystyle B\frac { 1+ (C - D) y(x)}{y'(x)}$

Если $D \ge C$ , это приводит к равному распределению средств.

Комментарий. Получается, что C = D - математическое представление золотого правила: "Поступай с другим так, как ты бы хотел, чтобы поступали с тобой"

Интересно, что D можно обеспечить двумя фундаментально различными способами: через развитое и культивируемое чувство сострадания, или через насилие и репрессии. Но в любом случае, это выглядит, как что-то порожденное социумом, культурой. Будем называть коэффициент D «социальным коэффициентом».

Выводы

Исходя из самых общих соображений, мы увидели, что введение «зависти» в нашу математическую модель привело к неравномерному распределению доходов.

Если бы мы не сравнивали свой доход с доходом других и довольствовались «тем, что есть», просто получая удовольствие от тех благ, которые нам достаются, без оглядки на других, то распределение было бы справедливым.

Чем выше коэффициент зависти, тем менее справедливо распределение, и в пределе мы очень быстро скатываемся в крайнюю форму, когда небольшая группка людей на вершине пирамиды имеет теоретически бесконечно больший доход, чем остальные.

Коэффициент зависти может быть скомпенсирован социально через два диаметрально противоположных подхода: сострадание или насилие.

Это то, что мы получили в нашем моделировании, и это мне кажется вполне правдоподобным. Однако, можем ли мы сделать какие-либо выводы из непроверенной и довольно примитивной модели: мы учли лишь несколько факторов и при этом взяли удобные для расчета функции? И все же мне кажется, что да, можем.

Конечно, мы не ответим на вопрос, движемся ли мы в ад или в рай, но основной вывод, который я вижу здесь, заключается в том, что вполне возможно (и я склоняюсь к этой мысли) существуют объективные факторы, во многом определяющие этот путь. Эти факторы могут быть связаны с доступной энергией, которая в свою очередь определяет некоторые коэффициенты, и в зависимости от соотношения этих коэффициентов мы объективно можем быть склонны к той или иной форме сосуществования.

Так, возможно, в человеческой природе объективно заложен слишком высокий «коэффициент зависти» или какой-либо другой «негативный» коэффициент.

Можем ли мы компенсировать это?

Если мы говорим о материальном распределении, то может показаться, что есть простой путь: через законы и принуждение. Здесь очень многое зависит от того, насколько «коэффициент зависти» высок и насколько он важен для нас. И если сердца революционеров / реформаторов горят желанием сделать мир справедливым здесь и сейчас, а сопротивления человеческого материала слишком велико, то результатом являются репрессии, что мы уже как человечество проходили не раз.

Делает ли это нас счастливыми? Путь ли это в рай? И действительно ли мы добиваемся справедливости в этом случае? Ведь все равно существует иерархия, и на вершине пирамиды живется намного лучше, чем внизу.

Есть другой путь, гораздо более длинный и сложный — путь трансформации через сострадание, чему нас учат многие религии. Но достижимо ли это в рамках всего человечества?

Возможно, существуют какие-то объективные коэффициенты, которые позволят дать точный ответ на этот вопрос в будущем.