Квантовые компьютеры: без математики и философии
В этой статье я разберу по косточкам все тайны квантовых компьютеров: что такое суперпозиция (бесполезна) и запутанность (интересный эффект), могут ли они заменить обычные компьютеры (нет) и могут ли они взломать RSA (нет). При этом я не буду упоминать волновую функцию и столь раздражающих Bob и Alice, которых вы могли встречать в других статьях про квантовые машины.
Первое и самое главное, что нужно знать — квантовые компьютеры не имеют ничего общего с обычными. Квантовые компьютеры по своей природе — аналоговые, там нет бинарных операций. Вероятно, вы уже слышали про Кубиты, что у них есть состояние 0, 1 и 0–1 одновременно, и благодаря этому вычисления выполняются очень быстро: это заблуждение. Кубит — это магнит (обычно атом или электрон), подвешенный в пространстве, который может вращаться по всем трем осям. Собственно, вращение магнита в пространстве — это и есть операции квантового компьютера. Почему это может ускорить вычисления? Было очень сложно найти ответ, но самые стойкие читатели увидят его в конце статьи. Начнем разоблачения.
Суперпозиция
Прежде чем говорить про волшебное состояние 0–1 (суперпозиция), сначала разберемся, как положение магнита в 3D вообще становится нулем и единицей. При создании квантового компьютера принимается решение, что если полюс магнита N (на картинках ниже — синий) смотрит вверх — то это значение ноль, если вниз — единица. Когда запускается квантовая программа, все кубиты с помощью внешнего магнитного поля выстраиваются в ноль (вверх). После завершения квантовой программы (серии вращений кубитов) надо получить конечное значение кубитов (выполнить Измерение), но как это сделать? Кубиты крайне маленькие и нестабильные, на них негативно влияет тепловое излучение (поэтому их сильно охлаждают) и космические лучи. На кубит нельзя просто посмотреть и сказать, где у него сейчас полюс N. Измерение выполняется опосредованно, например, можно к кубиту снизу и сверху поднести магниты с полюсом N.
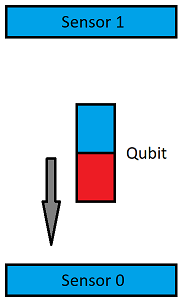
Если полюс кубита N был направлен вверх, то кубит упадет вниз, и как раз это падение можно зарегистрировать. После этого состояние кубита измерено (Ноль) и он физически больше непригоден для дальнейшего использования в квантовой программе. Это лишь иллюстративный пример, в каждом квантовом компьютере измерение выполняется своими методами и очень сложно найти описание — как именно, но суть остается та же.
Теперь самое интересное, вспоминаем, что наш магнит может вращаться в любом направлении, давайте положим его на бок? Именно с этого начинаются все квантовые алгоритмы.
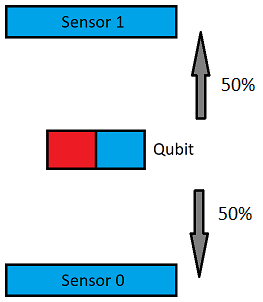
Браво, мы перевели кубит в состояние суперпозиции, знаменитое »0–1 одновременно». При попытке измерить такой кубит он будет падать вверх или вниз с вероятностью примерно 50% (зависит от точности построения квантового компьютера). Как вы видите, состояние кубита более чем конкретное, мы его только что просто повернули на 90o. Заявления о том, что он в нуле и единице одновременно (или мечется между ними) выглядят странно, ведь при измерении всегда сработает только один сенсор. Поворот еще на 90o выводит кубит из волшебного состояния.
Еще один важный момент: если кубит из вертикального положения повернуть не на 90o, а только на пару градусов, то при измерении он с очень высокой вероятностью будет падать на «Сенсор 0», а в редких случаях на «Сенсор 1». Это доказано опытами, я проверял это сам (IBM дает бесплатный доступ), одиночный атом ведет себя сложнее, чем обычный магнит.
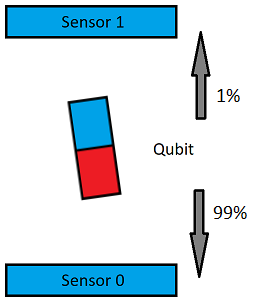
Любое отклонение от вертикали приводит к вероятности измерить единицу вместо нуля. Соответственно, исходную инициализацию кубитов и все вращения кубитов надо делать очень точно, защищать кубиты от внешнего воздействия надо очень надежно, иначе вы будете получать ошибку вычислений. Современные квантовые компьютеры имеют крайне низкую точность, это их большая проблема.
Теперь рассмотрим очень популярное, но ложное утверждение, что суперпозиция ускоряет вычисления. Все квантовые алгоритмы начинаются с перевода группы кубитов (регистра) в состояние суперпозиции (укладывания магнитов на бок), начиная с этого момента официальная наука заявляет нам, что каждый кубит хранит в себе 0–1 одновременно, два кубита хранят 0–3 одновременно, восемь кубитов 0–255 одновременно и т.д. Любое математическое действие над этой группой кубитов будет выполнено сразу для всех чисел, хранимых кубитами.
Пример: у нас есть две группы по 32 кубита (два регистра памяти), мы хотим посчитать сумму чисел из этих двух регистров. Выполнив сложение один раз мы получаем абсолютно все возможные комбинации сумм чисел, которые только можно разместить в двух регистрах по 32 бита, т.е. было выполнено около 18 квинтиллионов операций сложения за одну физическую операцию. Звучит очень круто, но есть подвох.
После завершения квантового алгоритма нам надо как-то вытащить результат вычисления, да вот беда — квантовый компьютер ни за что не отдаст нам все 18 квинтиллионов результатов за один раз. После измерения он вернет только один из них, причем рандомно. Процесс измерения разрушает кубиты, и чтобы получить еще один результат, нам придется выполнить операцию заново. Чтобы вытащить из квантовой машины все 18 квинтиллионов результатов придется запустить его как минимум 18 квинтиллионов раз. Звучит как фуфло.
Что там со взломом паролей? Аналогично, чтобы хэш-сумму перевести в пароль нужно запустить квантовую программу очень-очень много раз (как и на классическом компьютере). Таким образом, суперпозиция (даже если она реальна) сама по себе не имеет никакого эффекта на производительность квантовой машины.
Запутанность
Квантовая запутанность — второй кит, на котором держится квантовый компьютер, и это действительно любопытный эффект, который современная наука пока не может объяснить. Но мы пойдем издалека. Давайте взглянем на типичный кусок исходного кода для традиционного компьютера:
if (n > 50) then n = 50Эту строчку проблематично выполнить на квантовом компьютере, т.к. после операции (n>50) кубиты переменной n будут тут же физически разрушены (ведь их надо было измерить для операции сравнения), а эта переменная нужна нам дальше по коду. Условные переходы (как и циклы) недоступны для квантовых компьютеров, как они тогда вообще выживают? Одна операция IF все же может быть выполнена, без проведения измерения: контролируемое NOT (CNOT), это аналог классической операции XOR. В этой операции участвуют два кубита, контролирующий и контролируемый:
если полюс N контролирующего кубита направлен вниз (значение 1), то контролируемый кубит вращается на 180 градусов
если полюс N контролирующего кубита направлен вверх (значение 0), то контролируемый кубит не изменяется
Данная операция позволяет выполнять банальное сложение целых чисел для двух регистров кубитов. Чтобы выполнить эту операцию два кубита кратковременно подносят поближе друг к другу, после чего выполняют серию отдельных вращений. Измерения не требуются, т.е. с кубитами можно работать дальше. После этой операции кубиты запутаны. Как это проявляется? Начнем с банального:
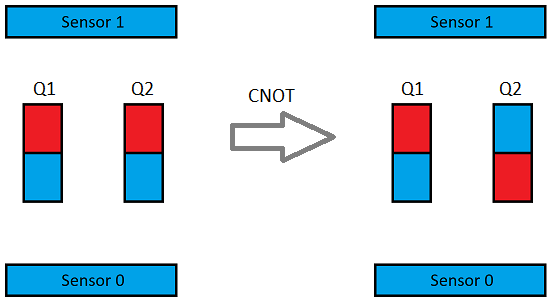
После того, как мы запутали кубиты, они становятся зависимыми друг от друга. Если кубит Q1 был измерен как Единица, то кубит Q2 будет измерен как Ноль. Но этот случай очевиден и не интересен, давайте перед CNOT уложим кубиты на бок:

Если контролирующий кубит лежит на боку, то контролируемый будет либо повернут на 180 градусов с вероятностью 50%, либо останется в прежнем состоянии. Точное итоговое положение кубитов в 3D пространстве после такой операции не известно (они якобы сразу во многих состояниях), ведь на кубиты нельзя посмотреть непосредственно. Но если запутанные кубиты измерить, то Q1 будет рандомно падать на сенсор 0 или 1, а Q2 будет всегда падать на противоположный сенсор.
Почему так происходит никто не знает. По логике, оба кубита лежат на боку, после операции CNOT они оба должны рандомно падать на оба сенсора, без какой-либо зависимости. По факту же прослеживается четкая связь при измерении (с некоторой погрешностью, система все-таки аналоговая). На этот счет есть две теории:
Официальная наука говорит, что кубиты обмениваются информацией между собой (неизвестно как, но мгновенно, больше скорости света). Когда первый кубит измеряют (бьют об сенсор), он сообщает второму кубиту куда именно упал, а тот его запоминает и при измерении ударится о противоположный сенсор. Эта теория выглядит весьма странно, но здесь надо понимать, что официальная наука цепко держится за принцип суперпозиции, что кубиты находятся в состоянии 0–1 одновременно: при измерении первого кубита второй не может больше оставаться в 0–1, ему надо срочно определиться с ориентацией.
Теория скрытых переменных: она говорит, что при взаимодействии кубиты сразу договариваются, кто на какой сенсор упадет, происходит это за счет изменения физического параметра кубита, который науке пока не известен. Эта теория выглядит более логичной, здесь уже не требуются сверхсветовые взаимодействия. Но данная теория отрицает наличие принципа суперпозиции, который является Святым Граалем для современной науки, поэтому всерьез эту теорию не прорабатывают.
На мой взгляд само явление Запутанности является главным доказательством, что Суперпозиции не существует, но я не физик-теоретик, поэтому оставим эту тему. В конце концов когда-то официальная наука высмеивала теорию движения литосферных плит, но в конце концов ребята во всем разобрались.
Пара заключительных моментов про запутанность:
Запутать можно сразу много кубитов, и это обычное дело для квантовых компьютеров, для этого надо прогнать CNOT поочередно для нескольких кубитов.
После операции CNOT контролирующий кубит на самом деле тоже меняет свою ориентацию в 3D пространстве. Его полюс N не двигается вверх-вниз, но сам кубит вращается вокруг оси Z, это явление называется Phase Kickback и оно имеет огромное значение для квантовых алгоритмов, именно оно дает ускорение вычислений. Об этом мы поговорим ниже.
Если после запутывания один из кубитов с помощью внешнего магнитного поля перевести в состояние Ноль (повторить первичную инициализацию), то это никак не повлияет на второй кубит, состояние запутанности будет разорвано. Т.е. обмен информацией на сверхсветовой скорости нельзя обеспечить за счет эффекта запутывания.
Запутанные частицы иногда сравнивают с носками: я надеваю один на правую ногу, второй автоматически становится левым. Это некорректное сравнение, запутанные частицы больше похожи на две монетки, стоящие на боку. Если одна из них упадет на Орла, то вторая точно упадет на Решко, даже если прошло несколько часов.
Чего не могут квантовые компьютеры
Квантовые компьютеры довольно медленные, типичная рабочая частота 100 МГц, но это поправимо. Они также довольно маленькие, 66 кубитов считается мега круто (можно разместить в памяти пару int), но это тоже поправимо. На физическом уровне квантовые компьютеры не поддерживают (и возможно, никогда не поддержат):
условные переходы и циклы (об этом я писал ранее);
умножение и деление;
возведение в степень и тригонометрию.
Все взаимодействие между кубитами сводится к операции CNOT, на которой далеко не уедешь. Но если они такие ограниченные, то почему вокруг них столько шума? При решении задачи в лоб никакого превосходства над классическими компьютерами не будет, но есть очень узкий перечень алгоритмов, где квантовый компьютер может себя проявить. Напомню, каждая квантовая операция — это вращение одного или двух кубитов, для ее выполнения достаточно одного кратковременного импульса. С другой стороны для моделирования вращения магнита на классическом компьютере нужно вычислить много синусов и косинусов. Примерно на этой особенности и строятся эффективные квантовые алгоритмы.
Алгоритм Шора
Алгоритмом Шора давно пугают интернеты, т.к. он теоретически может довольно быстро взломать RSA. Сама задача взлома сводится к поиску двух простых чисел, из которых состоит открытый ключ RSA, т.е. надо найти два делителя для очень большого числа (порядка 512 бит для RSA-512). Простой перебор на классическом или квантовом компьютере займет очень много времени, и как мы видели выше, принцип суперпозиции тут не спасает.
На самом деле есть два Алгоритма Шора, классический и с квантовым дополнением, начнем с первого. Математики определили, что задачу простого перебора можно заменить на следующее уравнение:
a — число 2 или 3 (на самом деле любое число, но 2 или 3 точно подойдут, какое именно из них — заранее нельзя сказать);
N — число, для которого ищем делители (условно — открытый ключ RSA);
mod — операция, которая возвращает остаток от целочисленного деления;
x — вспомогательное число, найдя его (простым перебором), мы быстро найдем делители числа N. Искомое x должно быть больше нуля, четным и минимальным из всех возможных.
Математики определили, что количество шагов по перебору числа x будет существенно меньше, чем простой перебор чисел a и b по формуле a*b=N. Я проверил как это работает, загнал формулы в Excel и нашел делители для числа 15: достаточно перебрать всего два числа x, проигнорировав 0 и все нечетные:
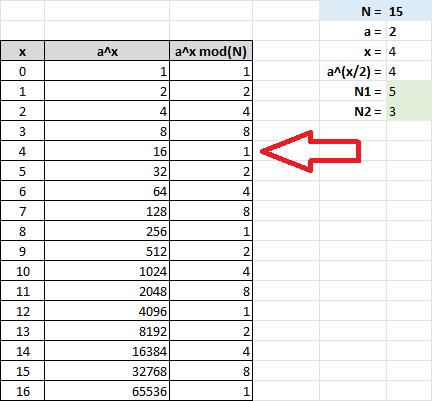
Этот эффект должен быть более выраженным для больших чисел, но есть подвох. Опытный глаз конечно же заметил операцию возведения в степень, а также поиск остатка от деления. Шагов перебора может и стало меньше, но каждый шаг сам по себе стал очень сложным, и их сложность будет расти экспоненциально для больших чисел N. Также вы уже наверняка задаетесь вопросом, причем тут квантовые компьютеры, если и в Excel все получилось?
Квантовый алгоритм Шора
Квантовый алгоритм Шора также начинается с вычисления формулы axmod (N), но тут возникает очень много проблем:
возведение в степень, умножение и деление (в том числе целочисленное с остатком) не поддерживаются на аппаратном уровне;
количество кубитов сильно ограничено и держать в памяти результат ax проблематично;
циклы не поддерживаются, значит перебор x надо делать без их участия.
Ребята не стали отчаиваться и придумали набор костылей. Число x на вход квантовой программы подается как рандомное. Если быть точнее, то набор кубитов (регистр) для хранения числа x переводится в суперпозицию (кубиты укладываются на бок). Начиная с этого момента официально заявляется, что axmod (N) будет выполнена сразу для всех возможных чисел x за одну операцию. Как мы видели выше, толку от этого мало, т.к. измерить мы сможем только один результат из всех, причем рандомный.
Далее, сама формула axmod (N) заменяется на очень странный код (показана симуляция квантового компьютера):
X = Register('X', 8)
F = Register('F', 4)
X.H()
F[3].X()
for i in range(8):
for j in range(2**i):
Fredkin(X[i], F[0], F[1])
Fredkin(X[i], F[1], F[2])
Fredkin(X[i], F[2], F[3])функция Register инициализирует указанное число кубитов (8 и 4), на выходе регистр кубитов, в которых можно хранить числа, по умолчанию сохраняется 0×0 (все полюса N направлены вверх);
метод H — Hadamard gate, укладывает кубиты на бок (переводит в суперпозицию);
метод X поворачивает кубит на 180o (аналог бинарного NOT);
функция Fredkin стандартная для квантовых вычислений, она меняет местами значения двух кубитов, если первый параметр (контролирующий) установлен в единицу. Функция сводится к 8 операциям CNOT и 9 одиночным вращениям кубитов;
входной регистр кубитов X хранит число x;
регистр F будет хранить результат вычисления axmod (N).
Полный исходный код доступен в моем репозитории.
Вы наверное очень удивлены, как это вообще может работать? Это костыль, который позволяет выполнять формулу axmod (N) для a=2 и N=15. Число x может быть любым. Есть отдельные методики, которые позволяют подобрать перечень вращений кубитов для любых чисел a и N. Как это работает, я не стал разбираться, поскольку документация на квантовые алгоритмы традиционно крайне низкого качества, но мои собственные опыты подтвердили, что вычисления выполняются корректно.
Соответственно, если мы хотим взломать какой-то ключ RSA-512, то сначала для этого конкретного ключа мы должны составить схему, которая будет включать в себя очень много вращений. Но сколько раз мы должны запустить такую схему? Вы обратили внимание на два вложенных цикла в исходном коде выше? Для числа N=15 схема запускается 255 раз, для N=21 — 511 раз, для пока недостижимого квантовым компьютерам N=35 будет 2047 запусков. Количество операций резко возрастает, в чем же профит квантового компьютера?
Quantum Phase Estimation
Поздравляю всех самых терпеливых читателей, пройдя долгий путь непонимания мы добрались до самой сути квантовых компьютеров. Когда мы вычисляем формулу F=axmod (N) на обычном компьютере, мы ждем появления значения F=1, чтобы объявить о взломе ключа RSA. Но когда мы работаем на квантовой машине, нам на самом деле не важно, что по итогу хранится в регистре F, решение задачи будет хранится во входном регистре X.
В классическом компьютере в операторе XOR (аналог CNOT) значение контролирующей переменной не меняется, но напомню, что когда в квантовой машине мы выполняем операцию CNOT, она меняет оба кубита:
полюс N контролируемого кубита двигается вверх-вниз, в зависимости от состояния контролирующего;
полюс N контролирующего кубита не двигается вверх-вниз, но сам кубит вращается по оси Z.

Отклонения кубита по оси Z называется фазой. За время выполнения квантовой программы все кубиты накапливают некоторое изменение фазы. Математики доказали, что, измерив итоговую фазу всех кубитов во входном регистре, можно с очень высокой вероятностью найти делители числа N (взломать RSA), даже если в F получилась не единица. Для RSA-512 нужно всего порядка 2000 запусков алгоритма на квантовом компьютере. Но есть подвох. Даже два.
Первая проблема заключается в том, что надо как-то суметь измерить фазу. Для этого используется алгоритм QFE (Quantum Phase Estimation), который требует дополнительных вращений кубитов на очень маленькие углы поворота. Для N=15 нужно вращать кубиты на 1.4o, для N=35 повороты будут уже 0.175o. Для RSA-512 нужно повернуть кубит на ничтожные 180/21022 градуса, сделав это 1022 раза. Кубиты — это аналоговая система, если ошибиться с углом поворота — на выходе мы получим ошибку. Современные квантовые компьютеры не могут справиться с числом N=35, им уже на этом этапе не хватает точности поворотов. Но это еще не так страшно, совсем ничтожными поворотами можно просто пренебречь, почти не потеряв точность всего алгоритма.
Вторая проблема заключается в вычислении axmod (N). Да, для RSA-512 надо вычислить ее всего лишь 2000 раз, но посмотрите еще раз на два вложенных цикла: одно такое вычисление — это более 21022 последовательных вращений кубитов. Это более чем фуфло. Квантовые компьютеры не способны взломать RSA, даже если они вырастут до миллиона кубитов. Есть большое количество научных статей, которые рассказывают нам, как им удалось оптимизировать эту часть и выполнить ее в сотни раз быстрее, но они всегда скромно умалчивают, сколько именно операций требуется, когда N = 2512.
Симуляторы квантовых компьютеров
Симуляторы квантовых компьютеров работают существенно медленнее своих реальных собратьев. Происходит это потому, что симуляторы делают свою работу гораздо честнее. Когда в симуляторе вы создаете регистр из 8 кубитов, то в памяти сохраняются все возможные значения для этих кубитов (создается массив на 256 ячеек). Если вы создадите два регистра по 8 бит и выполните операцию A+B, то симулятор посчитает и сохранит в памяти все возможные комбинации сложений (создаст массив на 65536 ячеек). Это будет существенно дольше, чем единичная операция, но после этого симулятор может вернуть вам все эти значения, не уничтожая данные при каждом «измерении».
Чтобы получить все варианты сложения на настоящем квантовом компьютере, вы будете запускать его как минимум 65536 раз (результат возвращается рандомно, могут быть повторы), и в целом, это займет даже больше времени, чем на симуляторе.
Но если кубиты — это просто магниты в 3D пространстве, можно ли создать симулятор, который вращает их в виртуальной реальности? Я попытался и создал библиотеку FastQubit. Большая часть операций действительно успешно работает (даже состояния Белла), и такой симулятор обладает существенным превосходством над обычным квантовым компьютером:
кубитов может быть много и они совершенно стабильны, никаких ошибок;
на кубиты можно посмотреть в любой момент времени, определить точное положение в 3D, при этом не разрушая их.
Но есть подвох. Phase Kickback в моей библиотеке работает не верно:
Q[0].H()
Q[1].X()
Q[0].P_pi(8)
Q[1].P_pi(8)
CNOT(Q[0], Q[1])
Q[1].P_pi(-8)
CNOT(Q[0], Q[1])Вот эта цепочка операций должна по итогу сдвинуть фазу кубита Q[0] на 45o, но в моем случае сдвиг выполнялся на 90o. Дело в том, что точное положение кубитов в 3D после первой операции CNOT науке не известно, тут обычно приплетают суперпозицию, что кубиты сразу много где. Я воспользовался документацией на квантовые операции, и сделал повороты ровно так, как они там описаны. Но нет, на самом деле никто не знает, какие повороты выполняются на самом деле.
Если вы заставите этот короткий код работать верно, то можете смело претендовать на Нобелевскую премию. Но не пытайтесь костылить: вы конечно можете добавить хак, который доворачивает фазу на нужный угол при определенных условиях, но это перестанет работать, когда в квантовую программу добавят запутанность сразу между несколькими кубитами.
Итоги
Документация на квантовые компьютеры максимально пафосная, даже элементарные вещи оборачиваются сложными формулами. Я потратил недели, чтобы разобраться, что на самом деле в них скрыто. Статьи в новостях и блогах наоборот крайне поверхностные, философские, и очень часто содержат ложную информацию. Никто и никогда не публикует цифру, сколько операций нужно выполнить, чтобы взломать RSA-512 (причем, он не самый стойкий), вместо этого вам покажут несколько формул вычисления сложности алгоритма, сделав это максимально непонятно.
Я не призываю немедленно прекратить финансирование всех программ по квантовым компьютерам, это фундаментальные исследования, которые могут принести неожиданные полезные результаты в других областях. Но необходимо прекратить публиковать страшилки про пост-квантовую эру.
