Как компьютер сам свой код улучшал, или программируем процесс программирования
На носу было придумывание темы для диплома, на кафедре популярностью пользовались различные варианты идей связанных с генетическими алгоритмами, а мне самому хотелось сделать что-нибудь этакое. Так и родилась идея, давшая начало данному проекту, а именно генетическому оптимизатору программного кода.
Цель была довольно амбициозной — в идеале сделать такую штуку, которой на вход подается программа, а дальше она ее крутит так и сяк и пытается всячески ускорить отдельные ее фрагменты без участия человека, попутно собирая себе базу для последующих оптимизаций. Сразу скажу что хотя в целом задача была решена, практической пользы я из нее извлечь не смог. Однако некоторые полученные в процессе результаты показались мне достаточно интересными чтобы ими поделиться.
Например вот такая забавная оптимизация набора арифметических инструкций (взятых из какой-то подвернувшейся под руку математической библиотеки), соответствующих формулам: , которая на 6 джаве с выключенным JIT у меня давала около 10% ускорения, при этом на первый взгляд даже не очевидно что эти формулы эквивалентны (ОТКУДА ТУТ OR? ЭТО ВООБЩЕ ЗАКОННО?!), хотя это так. Под катом я расскажу, как именно получались такие результаты и каким образом компьютер придумывал лучший код чем тот, который мог написать я сам.
Заняться я решил не абы какой оптимизацией, а так называемой «локальной» или peephole optimization. Это как правило последний этап через который прогоняют программы современные оптимизирующие компиляторы, и по сути он очень прост — они ищут заданные небольшие линейные последовательности инструкций и меняют их на другие, оптимальные с их точки зрения. То есть вот какая-нибудь пресловутая замена mov eax, 0 на xor eax eax — это вот как раз и есть локальная оптимизация. Самым интересным тут является то, каким именно образом эти правила замены строятся. Их могут составлять как вручную специально обученные и разбирающиеся в ассемблере люди, так и искать перебором наборов инструкций. Очевидно что первый вариант достаточно затратен (специально обученные люди наверняка захотят много денег) и малоэффективен (ну сколько таких наборов человек из головы сможет придумать и предусмотреть?), а второй — долог, особенно если пытаться перебирать длинные последовательности.
Вот тут на сцену и выходят генетические алгоритмы, позволяющие заметно сократить процесс перебора.
Про сами генетические алгоритмы я тут рассказывать не буду, надеюсь все хотя бы в общих чертах представляют что это такое, а кто не представляет — на хабре достаточно статей на эту тему, например вот. Остановлюсь только на том, как именно я их применял.
Достаточно очевидно, что особи в нашем случае — это фрагменты кода, операторы скрещивания и мутации должны каким-то образом модифицировать входящие в них инструкции, а фитнес-функция — отбирать наиболее быстрые варианты (так как оптимизировать мы будем именно скорость выполнения). Вот только как именно должно работать это самое скрещивание?
Скрещивание и мутация фрагментов кода
От идеи меняться произвольными фрагментами я отказался очень быстро. В этом случае очень велика вероятность получения невалидного кода — такого, который просто не получится запустить. В качестве своей целевой архитектуры я выбрал JVM (из-за простоты как самого байткода так и средств манипулирования им, хотя позже я уже понял что это было не самое удачное решение), а в ней достаточно строгий валидатор, который просто не даст загрузить кривой код (например вызывающий опустошение стека). Соответственно и значение фитнес-функции для него посчитать не выйдет.
Поэтому пришлось соорудить достаточно сложную систему, практически этакий мини-эмулятор JVM. Для каждой инструкции и каждой их последовательности определялись начальное и конечное состояние. Конкретные значения не вычислялись, определялись только типы операндов. То есть всегда можно было сказать сколько значений и каких типов снималось и клалось на стек в результате выполнения произвольного фрагмента кода. Затем на основе этой информации находился другой набор, которым можно заменить данный (в случае мутации он создавался случайно, в случае скрещивания — искался во второй особи), для сохранения корректности кода он должен был быть эквивалентен в плане обращения с состоянием JVM — то есть снимать со стека и класть обратно ровно то же количество и типы значений.
Это не относится к промежуточным вычислениям, то есть фрагмент внутри себя может делать со стеком что угодно, но после себя должен оставить ровно такое же состояние.
Пример:
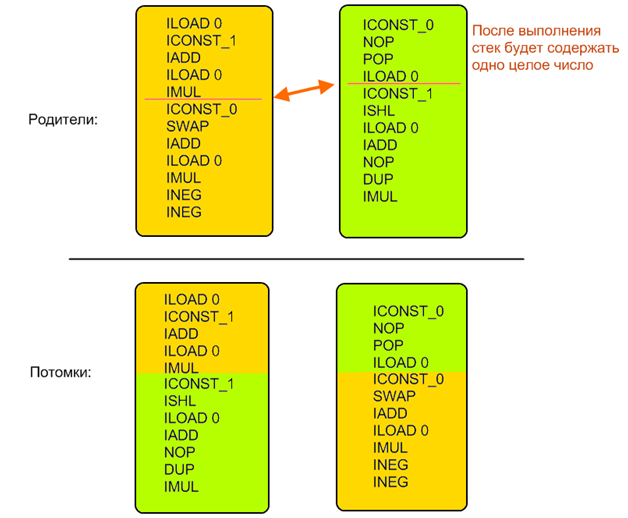
Начальное поколение создавалось по этим же правилам — оно должно было изменять состояние JVM таким же образом как и исходная последовательность инструкций. Таким образом всегда поддерживалась корректность особей и их сравнимость: поскольку все особи после своей работы всегда оставляли одинаковое состояние (значения одних и тех же типов на стеке в одном и том же порядке) то легко было сравнивать похожесть получаемых результатов с референсными: достаточно было просто посчитать длину многомерного вектора, в котором каждое значение — это один регистр или элемент стека (я тут периодически использую как джавовскую так и не-джавовскую терминологию так как в принцип алгоритм применим к любому виду вычислительной машины, и я сам его проверял на нескольких целях).
Фитнес-функция
Что же нам нужно от наших особей? А нужно нам чтобы они во-первых считали те же самые результаты, а во-вторых — делали это быстрее исходной. А чтобы это проверить — нам их надо запустить.
У нас уже есть посчитанные состояния VM на каждом шаге выполнения наших особей. В частности это дает нам необходимый набор входных данных — то есть то, какие регистры надо заполнить и сколько и каких элементов на стек положить чтобы все сработало как надо. Отлично, дописываем к началу каждой особи один и тот же код, который будет эти данные создавать, а к концу — который будет записывать результаты куда нам надо. Итоговое значение фитнес-функции составим из расстояния между векторами результатов и коэффициента ускорения по сравнению с оригиналом.
По ходу исследований выяснилось, что «лобовая» реализация приводит к быстрому вырождению популяции, которая забивается очень короткими (и очень быстрыми) особями, которые не делают ничего полезного (то есть вместо вычислений, например, просто опустошают стек до нужной глубины), но при этом выигрывают за счет длины и скорости. Поэтому пришлось сделать так, что скорость начинает учитываться только после того, как вычисленные результаты становятся достаточно близкими к референсным.
Помимо скорости работы и эквивалентности результатов оказалось необходимым дополнительно контролировать длину особей. Без такого контроля в популяции достаточно быстро (примерно за 50 поколений) начинается рост средней длины особи, вплоть до 10–20 длин исходного фрагмента кода. Появление таких длинных особей сильно замедляет генетический процесс, так как во-первых увеличивается время анализа кода, необходимого для проверок корректности (растет время каждой итерации), а во-вторых для получения решения необходимо избавиться от большого числа ненужных инструкций в особи, что может занимать значительное число поколений (растет общее число итераций).
Поскольку в данной работе исследуется оптимизация скорости выполнения, а не размера набора инструкций, коэффициент длины используется только для отсева слишком длинных кандидатов и применяется к формуле только если особь, для которой вычисляется фитнес-функция, длиннее исходной.
Итоговый вид фитнес-функции:
Здесь — тестируемая особь,
— оригинальный фрагмент, diff — разность векторов результатов, len — отношение длинн, speedup — отношение времени выполнения.
speedup приравнивается к единице если diff больше некоторой константы, то есть скорость начинает учитываться только для считающей почти правильные значения особи.
Нетрудно убедиться что данная функция обладает следующими свойствами:
- Она близка к нулю для начальных случайных фрагментов кода (велика разница результатов)
- Она приближается к единице по мере схождения вычисляемых результатов с референсными
- Она равна единице для исходного фрагмента
- Все варианты с фитнес-функцией большей единицы — потенциальные результаты работы нашего алгоритма, это те особи которые считают что надо и при этом быстрее/короче
Верификация
По ходу работы алгоритма каждая особь проверялась на соответствие результатов тем, что давал исходный фрагмент на нескольких десятках тестовых примеров. Это быстрая и достаточно эффективная проверка, но она явно недостаточна для строгого доказательства эквивалентности полученной оптимизированной последовательности и исходной. Чтобы такое доказательство получить использовалась формальная верификация.
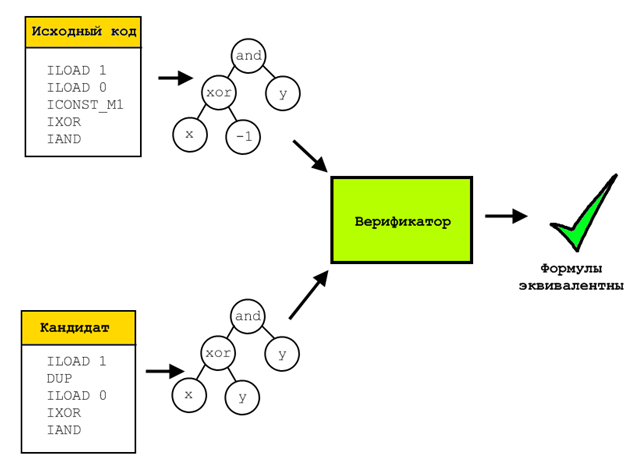
Для этого для верифицируемой и исходной особей все их операции представлялись в символьном виде, то есть после прогона через специальный эмулятор в каждом регистре/ячейке стека лежало символьное представление вычисленной и записанной в него формулы. Затем все эти формулы сравнивались с помощью решателя SMT-выражений Z3. Такой решатель способен доказать, что не существует набора входных параметров, на которых две проверяемые формулы дадут разный результат. Если же такой набор существует, то он будет построен и предъявлен.
Поскольку верификация эта достаточно длительный процесс (могла занимать десятки минут для одной особи и пары простейших математических выражений) то подвергались ей только кандидаты в окончательное решение, то есть особи с фитнес-функцией большей 1.
Впрочем стоит отметить что в ходе исследований не встретился ни один кандидат, который бы вычислял все правильно на тестовых наборах данных, но отсеивался бы на этапе верификации.
Примеры
Генетические алгоритмы, как и любая наверное отрасль машинного обучения — удивительная вещь, периодически заставляющая программиста хвататься за голову и кричать «как, как он это сделал?». Пикантности тут добавляло то, что в моем случае с моей помощью компьютер фактически улучшает сам свои программы каким-то неведомым образом, придумывая такие штуки до которых я сам сходу додуматься бы не смог.
В общем я иногда ощущал себя героем этого и подобных комиксов:

Ну вот мы прогнали наших особей через скрещивания и эмуляции, проверифицировали эквивалентность результатов и что же мы получили? Приведу пару примеров найденных мной оптимизаций.
Сворачивание констант и прочие стандартные штуки
Во-первых алгоритм достаточно хорошо находит всякие стандартные вещи на синтетических тестах, типа удаления неиспользуемых вычислений или свертывания констант, хотя под это специально я его не затачивал. Например довольно быстро он понял что можно сократить до
:
Было:
ILOAD 0
ICONST_1
IADD
ICONST_2
ICONST_M1
IMUL
IADD
Стало:
ILOAD 0
ICONST_1
ISUB
Все остальные примеры взяты из реального кода, была написана специальная тулза которая парсила скомпилированные классы и искала в них подходящие последовательности для оптимизации (то есть не содержащие ветвлений и неподдерживаемых инструкций).
Упрощение математических выражений и вынесение за скобки
Пример из начала статьи сократился с 11 до 9 инструкций. Вместо алгоритм вывел показанный ранее
. На первый взгляд выражение вообще неправильное, и получив его я бросился искать ошибку в коде эмулятора. Ан нет, все верно, так как выражение
всегда четное и неотрицательное, то есть младший бит у него всегда ноль, а в таком случае сложение с единицей эквивалентно xor с ней же, а работает видимо на какие-то доли быстрее. Правда только в отсутствии JIT, если его включить то на первое место выходит вполне ожидаемое
. Уж не знаю почему вариант с OR (или с XOR) работал быстрее, но этот результат был регулярно воспроизводим, в том числе на разных версиях джавы и на разных компьютерах
Вообще JIT в случае с джавой принес очень много головной боли, и я даже пожалел что выбрал эту платформу. Никогда нельзя было быть уверенным на все сто, это твоя оптимизация увеличила скорость, или это чертова джава-машина внутри себя что-то там провернула. Я конечно изучил всякие полезны статьи типа Анатомия некорректных микротестов оценки производительности, но все равно намучался с ней изрядно. Очень раздражало последовательное улучшение кода, зависящее от числа запусков. Запустил фрагмент сто раз — он работает в режиме интерпретатора и дает один результат, запустил тысячу — включился JIT, перевел в нативный код, но особо не оптимизировал, запустил десять тысяч — JIT принялся что-то ковырять в этом нативном коде, в итоге скорости выполнения меняются на порядки и все это приходится учитывать.
Логические операторы
Впрочем кое-где мне даже JIT удалось обскакать. Например выражение (x XOR -1)AND y Достаточно очевидной оптимизацией для него будет ! x and y, и это именно то что сгенерирует для него вам компилятор С++. Но в байткоде джавы нет операции побитового однооперандного не, так что оптимальным вариантом здесь будет (x XOR y) AND y. При этом JIT до такого уже не додумывается (проверялось включением дебажного вывода на server JVM 1.6), что позволяет немного выиграть по скорости.
Хитрая особенность сдвига влево
Был еще один забавный результат с оператором сдвига. Где-то в недрах BigInteger было найдено выражение (x & 31)<<1, оптимизированной версией которого алгоритм выдал x << 1.
Опять хватание за голову, опять поиски бага — очевидно ведь что алгоритм взял и выкинул целый значимый кусок кода. Пока я не додумался повнимательнее перечитать спецификацию операторов, в частности оказалось что оператор << использует только 5 младших бит своего первого операнда. Поэтому явный &31 в общем-то не нужен, оператор сделает это за тебя (я так понял что в байткоде библиотечных классов принудительный & оставлен для совместимости со старыми версиями, так как эта фишка появилась не в самой первой джаве).
Проблемы и заключение
Получив свои результаты я начал думать что с ними делать дальше. И вот тут как раз ничего и не придумалось. Оптимизации мои в случае с джавой слишком малы и незаметны чтобы оказать существенное влияние на скорость работы программы в целом, во всяком случае для тех программ на которых я мог все это тестировать (может какие-нибудь глубоконаучные вычисления и выиграют заметно от замещения пары инстркций и сокращения времени одного такта на пару наносекунд). К тому же эффект значительно съедается самой структурой джава-машины, виртуальностью и JIT.
Я попробовал перейти на другие архитектуры. Сперва на x86, получил первую работающую версию, но ассемблер там слишком сложный и написать требующийся для его верификации код оказалось мне не под силу. Затем я попробовал ткнуться в сторону шейдеров, благо работал тогда в геймдеве, и добавил поддержку для пиксельного шейдерного ассемблера. Но там я просто не смог найти ни одного подходящего шейдера, содержащего хороший пример последовательности инструкций.
В общем так и не придумал куда это дело прикрутить. Хотя ощущение от того, когда компьютер оказывается умнее тебя и находит такую оптимизаци, которую ты даже не сразу сам можешь понять как она работает, я запомнил надолго.
