Julia и уравнения в частных производных09.11.2018 11:19

leqgbus1-oqmdy3ndivqv_552ws.png

На примере типичнейших физических моделей закрепим навыки работы с функциями и познакомимся с быстрым, удобным и красивым визуализатором PyPlot, предоставляющим всю мощь питоновской Matplotlib. Будет много картинок (упрятанных под спойлеры)

Удостоверяемся, что под капотом всё чистое и свежее:


Под капотом 
]status
Status `C:\Users\Игорь\.julia\environments\v1.0\Project.toml`
  [537997a7] AbstractPlotting v0.9.0
  [ad839575] Blink v0.8.1
  [159f3aea] Cairo v0.5.6
  [5ae59095] Colors v0.9.5
  [8f4d0f93] Conda v1.1.1
  [0c46a032] DifferentialEquations v5.3.1
  [a1bb12fb] Electron v0.3.0
  [5789e2e9] FileIO v1.0.2
  [5752ebe1] GMT v0.5.0
  [28b8d3ca] GR v0.35.0
  [c91e804a] Gadfly v1.0.0+ #master (https://github.com/GiovineItalia/Gadfly.jl.git)
  [4c0ca9eb] Gtk v0.16.4
  [a1b4810d] Hexagons v0.2.0
  [7073ff75] IJulia v1.13.0+ [`C:\Users\Игорь\.julia\dev\IJulia`]
  [6218d12a] ImageMagick v0.7.1
  [c601a237] Interact v0.9.0
  [b964fa9f] LaTeXStrings v1.0.3
  [ee78f7c6] Makie v0.9.0+ #master (https://github.com/JuliaPlots/Makie.jl.git)
  [7269a6da] MeshIO v0.3.1
  [47be7bcc] ORCA v0.2.0
  [58dd65bb] Plotly v0.2.0
  [f0f68f2c] PlotlyJS v0.12.0+ #master (https://github.com/sglyon/PlotlyJS.jl.git)
  [91a5bcdd] Plots v0.21.0
  [438e738f] PyCall v1.18.5
  [d330b81b] PyPlot v2.6.3
  [c4c386cf] Rsvg v0.2.2
  [60ddc479] StatPlots v0.8.1
  [b8865327] UnicodePlots v0.3.1
  [0f1e0344] WebIO v0.4.2
  [c2297ded] ZMQ v1.0.0


Иначе докачиваем всё что нужно на сегодня 
julia>]
pkg> add PyCall
pkg> add LaTeXStrings 
pkg> add PyPlot
pkg> build PyPlot # если не произошел автоматический build
# в случае нытья - просто качайте всё что он попросит, питон довольно требовательный
pkg> add Conda # это для использования Jupyter - очень удобная штука
pkg> add IJulia # вызывается как на заглавной картинке
pkg> build IJulia # если не произошел автоматический build

Теперь к задачам!


Уравнение переноса

В физике под термином перенос понимают необратимые процессы, в результате которых в физической системе происходит пространственное перемещение (перенос) массы, импульса, энергии, заряда или какой-либо другой физической величины.
Линейное одномерное уравнение переноса (или уравнение адвекции) — простейшее дифференциальное уравнение в частных производных — записывается в виде

$ \frac{\partial U(x,t)}{\partial t}+c\frac{\partial U(x,t)}{\partial x}=\Phi(U,x,t) $

Для численного решения уравнения переноса можно использовать явную разностную схему:

$ \frac{\hat{U}_i-U_i}{\tau}+c\frac{U_i-U_{i-1}}{\Delta}=\frac{\Phi_{i-1}+\Phi_i}{2} $

где $\hat{U}$ — значение сеточной функции на верхнем временном слое. Эта схема устойчива при числе Куранта $K=c\tau/\Delta<1$


Нелинейный перенос

$ \frac{\partial U(x,t)}{\partial t}+(C_0+UC_1)\frac{\partial U(x,t)}{\partial x}=\Phi(U,x,t) $

Линейный источник (перенос с поглощением): $\Phi(U,x,t)=-BU$. Воспользуемся явной разностной схемой:

$ U^{j+1}_i=\left(1-\frac{h_tB}{2}-\frac{h_tC_0}{h_x}-\frac{h_tC_1}{h_x}U^j_i\right)U^j_i+U^j_{i-1}\left(\frac{h_tC_0}{h_x}-\frac{h_tB}{2}+\frac{h_tC_1}{h_x}U^j_i\right) $

using Plots
pyplot()

a = 0.2
b = 0.01
ust = x -> x^2 * exp( -(x-a)^2/b ) # начальное условие
bord = t -> 0. # граничное

# можно задавать значения по-умолчанию
function transferequi(;C0 = 1., C1 = 0., B = 0., Nx = 50, Nt = 50, tlmt = 0.01)
    dx = 1/Nx
    dt = tlmt/Nt

    b0 = 0.5B*dt
    c0 = C0*dt/dx
    c1 = C1*dt/dx

    print("Kurant: $c0 $c1")

    x = [i for i in range(0, length = Nx, step = dx)]# один из способов задать массив с помощью цикла
    t = [i for i in range(0, length = Nt, step = dt)] # ранжированая переменная - не массив

    U = zeros(Nx, Nt)

    U[:,1] = ust.(x)
    U[1,:] = bord.(t)

    for j = 1:Nt-1, i = 2:Nx
        U[i, j+1] = ( 1-b0-c0-c1*U[i,j] )*U[i,j] + ( c0-b0+c1*U[i,j] )*U[i-1,j]
    end

    t, x, U
end

t, X, Ans0 = transferequi( C0 = 4., C1 = 1., B = 1.5, tlmt = 0.2 )

plot(X, Ans0[:,1], lab = "t1")
plot!(X, Ans0[:,10], lab = "t10")
p = plot!(X, Ans0[:,40], lab = "t40")
plot( p, heatmap(t, X, Ans0) ) # объединим одним в одно изображение


Результат

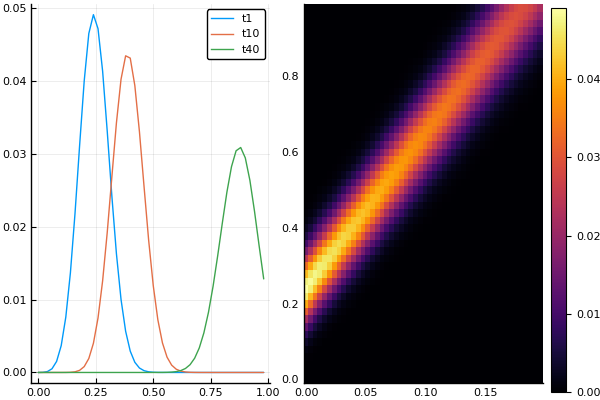
_bvff4raqmidxnuxew6lyy8mh3w.png

Усилим поглощение: 

t, X, Ans0 = transferequi( C0 = 2., C1 = 1., B = 3.5, tlmt = 0.2 )

plot(X, Ans0[:,1])
plot!(X, Ans0[:,10])
p = plot!(X, Ans0[:,40])
plot( p, heatmap(t, X, Ans0) )


Результат

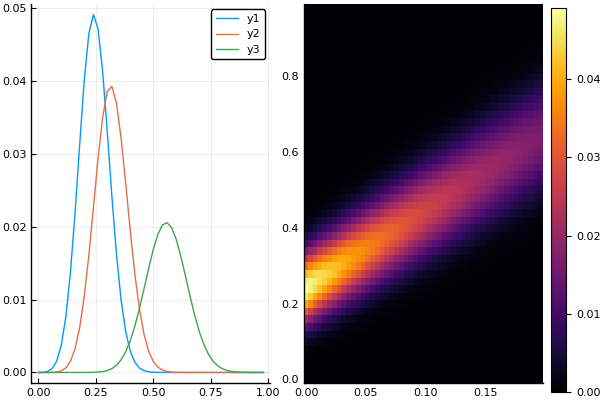
uoucm8stif37xzff9scatjuhbyw.png

t, X, Ans0 = transferequi( C0 = 1., C1 = 15., B = 0.1, Nx = 100, Nt = 100,  tlmt = 0.4 )

plot(X, Ans0[:,1])
plot!(X, Ans0[:,20])
plot!(X, Ans0[:,90])


Почти опрокинулась

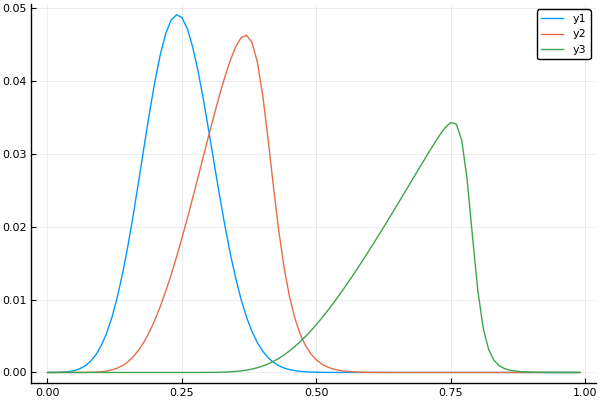
lnptud2faxzdhsdp1xpyrxcb1ga.png
heatmap(t, X, Ans0)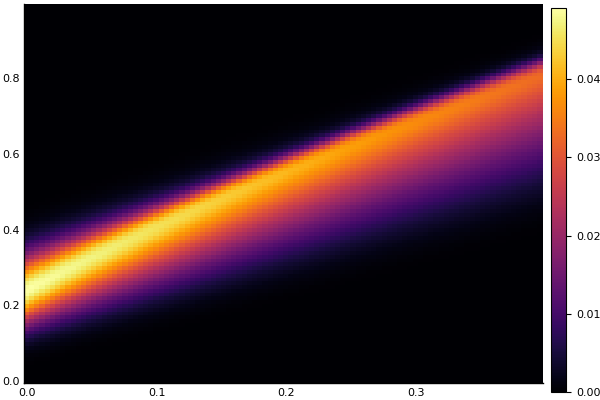
pg3n1gov-hdzer-ip7a24mmulfq.png


Уравнение теплопроводности

Дифференциальное уравнение теплопроводности (или уравнение диффузии тепла) записывается следующим образом:

$ \frac{\partial T(x,t)}{\partial t}+D\frac{\partial^2 U(x,t)}{\partial x^2}=\phi(T,x,t) $

Это уравнение параболического типа, содержащее первую производную по времени t и вторую по пространственной координате x. Оно описывает динамику температуры например, остывающего или нагреваемого металлического стержня (функция T описывает профиль температуры по координате х вдоль стержня). Коэффициент D называется коэффициентом теплопроводности (диффузии). Он может быть как постоянным, так и зависеть, как явно от координат, так и от самой искомой функции D (t, x, T).

Рассмотрим линейное уравнение (Коэффициент диффузии и источники тепла не зависят от температуры). Разностная аппроксимация дифференциального уравнения с помощью явной и неявной схемы Эйлера соответственно:

$ \frac{T_{i,n+1}-T_{i,n}}{\tau}=D\frac{T_{i-1,n}-2T_{i,n}+T_{i+1,n}}{\Delta^2}+\phi_{i,n} \\ \frac{T_{i,n+1}-T_{i,n}}{\tau}=D\frac{T_{i-1,n+1}-2T_{i,n+1}+T_{i+1,n+1}}{\Delta^2}+\phi_{i,n} $

δ(x) = x==0 ? 0.5 : x>0 ? 1 : 0 # дельта-функция с использованием тернарного оператора
startcond = x-> δ(x-0.45) - δ(x-0.55) # начальное условие
bordrcond = x-> 0. # условие на границе
D(u) = 1 # коэффициент диффузии
Φ(u) = 0 # функция описывающая источники
# чтоб ввести греческую букву вводим LaTex команду и жмем Tab
# \delta press Tab -> δ

function linexplicit(Nx = 50, Nt = 40; tlmt = 0.01)
    dx = 1/Nx
    dt = tlmt/Nt
    k = dt/(dx*dx)

    print("Kurant: $k dx = $dx dt = $dt k<0.5? $(k<0.5)")

    x = [i for i in range(0, length = Nx, step = dx)] # один из способов задать массив с помощью цикла
    t = [i for i in range(0, length = Nt, step = dt)] # ранжированая переменная - не массив
    U = zeros(Nx, Nt)

    U[: ,1] = startcond.(x)
    U[1 ,:] = U[Nt,:] = bordrcond.(t)

    for j = 1:Nt-1, i = 2:Nx-1
        U[i, j+1] = U[i,j]*(1-2k*D( U[i,j] )) + k*U[i-1,j]*D( U[i-1,j] ) + k*U[i+1,j]*D( U[i+1,j] ) + dt*Φ(U[i,j])
    end
    t, x, U
end

t, X, Ans2 = linexplicit( tlmt = 0.005 )

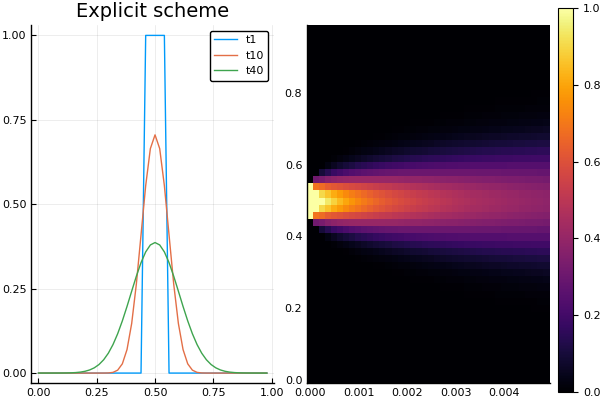
plot(X, Ans2[:,1], lab = "t1")
plot!(X, Ans2[:,10], lab = "t10")
p = plot!(X, Ans2[:,40], lab = "t40", title = "Explicit scheme")
plot( p, heatmap(t, X, Ans2) )


Результат

omhtoq-yyo33ksadghqjqijbzds.png


Воспользуемся неявной схемой и методом прогонки 
function nonexplicit(Nx = 50, Nt = 40; tlmt = 0.01)
    dx = 1/Nx
    dt = tlmt/Nt
    k = dt/(dx*dx)

    print("Kurant: $k dx = $dx dt = $dt k<0.5? $(k<0.5)\n")

    x = [i for i in range(0, length = Nx, step = dx)]
    t = [i for i in range(0, length = Nt, step = dt)]
    U = zeros(Nx, Nt)
    η = zeros(Nx+1)
    ξ = zeros(Nx)

    U[: ,1] = startcond.(x)
    U[1 ,:] = bordrcond.(t)
    U[Nt,:] = bordrcond.(t)

    for j = 1:Nt-1
        b = -1 - 2k*D( U[1,j] )
        c = -k*D( U[2,j] )
        d = U[1,j] + dt*Φ(U[1,j])
        ξ[2] = c/b
        η[2] = -d/b

        for i = 2:Nx-1

            a = -k*D( U[i-1,j] )
            b = -2k*D( U[i,j] ) - 1
            c = -k*D( U[i+1,j] )
            d = U[i,j] + dt*Φ(U[i,j])

            ξ[i+1] = c / (b-a*ξ[i])
            η[i+1] = (a*η[i]-d) / (b-a*ξ[i])
        end

        U[Nx,j+1] = η[Nx]

        for i = Nx:-1:2
            U[i-1,j+1] = ξ[i]*U[i,j+1] + η[i]
        end
    end
    t, x, U
end

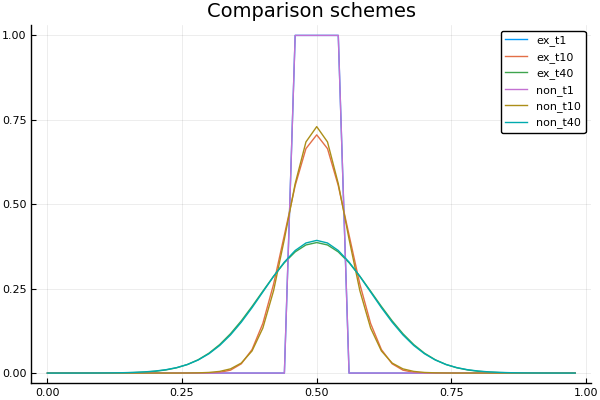
 plot(X, Ans2[:,1], lab = "ex_t1")
plot!(X, Ans2[:,10], lab = "ex_t10")
plot!(X, Ans2[:,40], lab = "ex_t40")
plot!(X, Ans3[:,1], lab = "non_t1")
plot!(X, Ans3[:,10], lab = "non_t10")
plot!(X, Ans3[:,40], lab = "non_t40", title = "Comparison schemes")

Сравнение схем

nhku2yqripfgweqqaakesnly6k0.png


Нелинейное уравнение теплопроводности

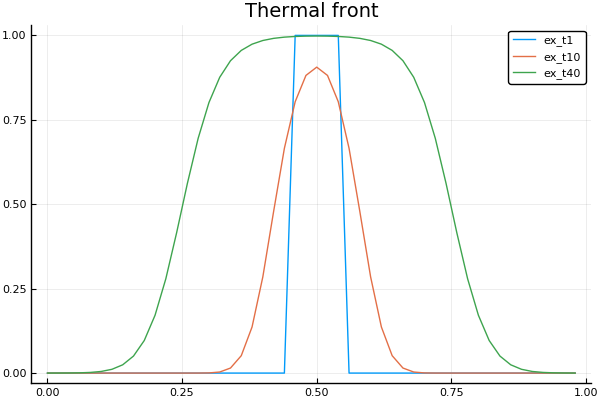
Намного более интересные решения можно получить для нелинейного уравнения теплопроводности, например, с нелинейным источником тепла $\phi(x,T)=10^3(T-T^3)$. Если задать его в таком виде, то получится решение в форме тепловых фронтов, распространяющихся в обе стороны от зоны первичного нагрева

Φ(u) = 1e3*(u-u^3)

t, X, Ans4 = linexplicit( tlmt = 0.005 )

plot(X, Ans4[:,1], lab = "ex_t1")
plot!(X, Ans4[:,10], lab = "ex_t10")
plot!(X, Ans4[:,40], lab = "ex_t40", title = "Thermal front")


Тепловой фронт

9u5n9nxsyc4jts0enx5gnyafx1o.png

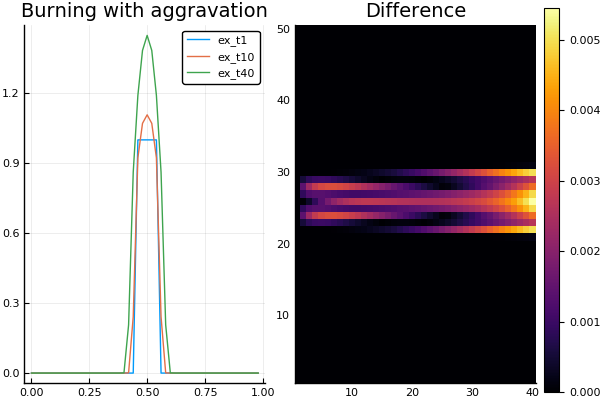
Еще более неожиданные решения возможны при нелинейности также и коэффициента диффузии. Например, если взять $D(x,T)=T^2$, a $\phi(x,T)=10^3T^{3.5}$, то можно наблюдать эффект горения среды, локализованный в области ее первичного нагрева (S-режим горения «с обострением»).
Заодно проверим, как наша неявная схема работает с нелинейностью и источников и коэффициента диффузии

D(u) = u*u
Φ(u) = 1e3*abs(u)^(3.5)

t, X, Ans5 = linexplicit( tlmt = 0.0005 )
t, X, Ans6 = nonexplicit( tlmt = 0.0005 )

plot(X, Ans5[:,1], lab = "ex_t1")
plot!(X, Ans5[:,10], lab = "ex_t10")
p1 = plot!(X, Ans5[:,40], lab = "ex_t40", title = "Burning with aggravation")
p2 = heatmap(abs.(Ans6-Ans5), title = "Difference") 
# построим разницу между результатами схем
plot(p1, p2)


S-режим

no3-ol6eesemjyojp_xul9lbgw0.png


Волновое уравнение

Волновое уравнение гиперболического типа

$ \frac{\partial^2 U(x,t)}{\partial t^2}=c^2\frac{\partial^2 U(x,t)}{\partial x^2} $

описывает одномерные линейные волны без дисперсии. Например, колебания струны, звук в жидкости (газе) или электромагнитные волны в вакууме (в последнем случае уравнение должно быть записано в векторном виде).

Простейшей разностной схемой, аппроксимирующей данное уравнение, является явная пятиточечная схема

$ \frac{U^{n+1}_i-2U^{n}_i+U^{n-1}_i}{\tau^2}=c^2\frac{U^n_{i+1}-2U^n_i+U^n_{i-1}}{h^2}\\ x_i=ih,\,t_n=\tau $

Эта схема, получившая название «крест», имеет второй порядок точности по времени и по пространственной координате и является трехслойной по времени.

# функция задающая начальное условие
ψ = x -> x^2 * exp( -(x-0.5)^2/0.01 )
# поведение на границах
ϕ(x) = 0
c = x -> 1

# решение одномерного волнового уравнения
function pdesolver(N = 100, K = 100, L = 2pi, T = 10, a = 0.1 )

    dx = L/N;
    dt = T/K;
    gam(x) = c(x)*c(x)*a*a*dt*dt/dx/dx;
    print("Kurant-Fridrihs-Levi: $(dt*a/dx) dx = $dx dt = $dt")
    u = zeros(N,K); 

    x = [i for i in range(0, length = N, step = dx)]
    # инициализируем первые два временных слоя
    u[:,1] = ψ.(x);
    u[:,2] = u[:,1] + dt*ψ.(x);
    # задаём поведение на границах

    fill!( u[1,:], 0);
    fill!( u[N,:], ϕ(L) );

    for t = 2:K-1, i = 2:N-1
        u[i,t+1] = -u[i,t-1] + gam( x[i] )* (u[i-1,t] + u[i+1,t]) + (2-2*gam( x[i] ) )*u[i,t];
    end
    x, u
end

N = 50; # количество шагов по координате
K = 40; # и по времени
a = 0.1; # скорость распространения волны
L = 1; # длина образца 
T = 1; # длительность эксперимента

t = [i for i in range(0, length = K, stop = T)]

X, U = pdesolver(N, K, L, T, a) # вызываем расчетную функцию

plot(X, U[:,1])
plot!(X, U[:,40])


Результат

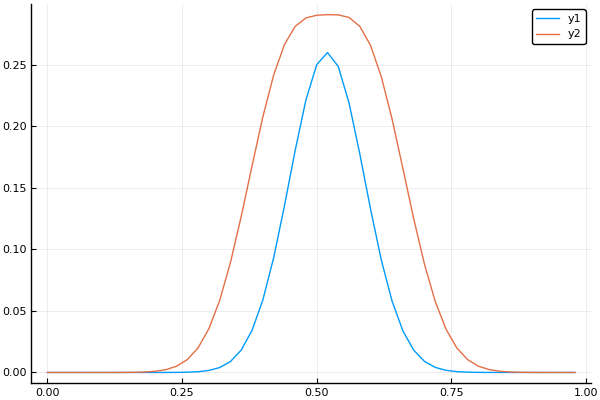
3nmdnsyyhnw6jtjg8vn1jzslksw.png

Чтобы построить поверхность, воспользуемся PyPlot’ом не как окружением Plots, а непосредственно:


График-поверхность 
using PyPlot
surf(t, X, U)

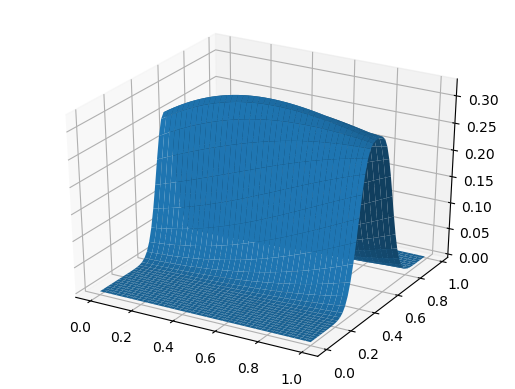
kl3n0sqntej1rta8lzjowahzby0.png

И на десерт распространение волны со скоростью зависящей от координаты: 

ψ = x -> x>1/3 ? 0 : sin(3pi*x)^2
c = x -> x>0.5 ? 0.5 : 1

X, U = pdesolver(400, 400, 8, 1.5, 1)
plot(X, U[:,1])
plot!(X, U[:,40])
plot!(X, U[:,90])
plot!(X, U[:,200], xaxis=("Распространение волнового фронта", (0, 1.5), 0:0.5:2) )


Результат

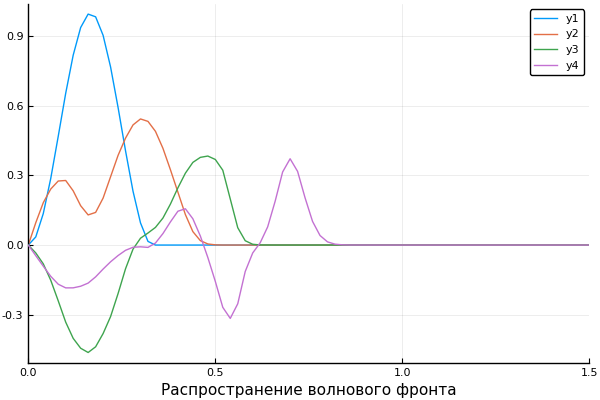
sk0aekgrt9l1w5uq2s-13ojwqqi.png

U2 = [ U[i,j] for i = 1:60, j = 1:size(U,2) ] # срежем пустую область
surf(U2) # такие вещи лучше смотреть с разных ракурсов

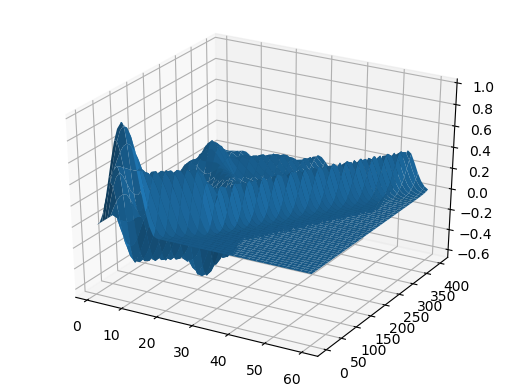
mas2sh_ng9kftusnxgv6nadf6bs.png

heatmap(U, yaxis=("Координаты возмущения", (0, 50), 0:10:50))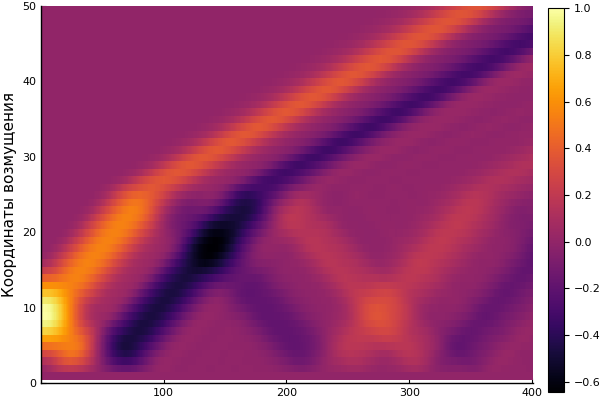
zxxiguguqwqnewgi9tjvqwp9vq4.png

На сегодня достаточно. Для более детального ознакомления:
ссылка PyPlot на гитхаб, еще примеры использования в качестве окружения Plots и хорошая русскоязычная памятка по Julia.

© Habrahabr.ru