Физическая программная археология
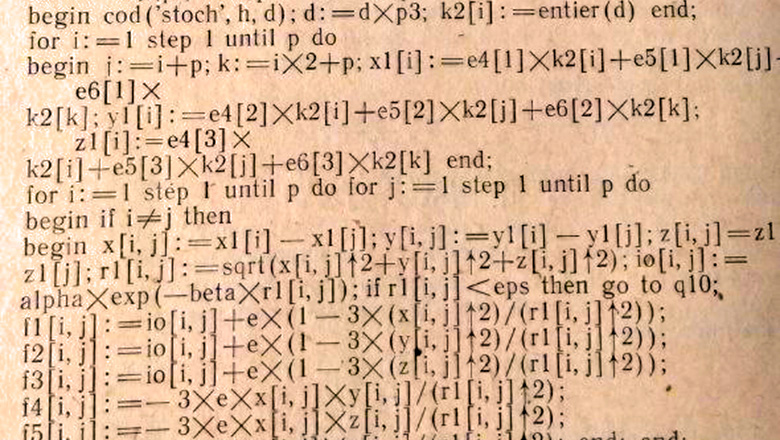
program NMR_rarefied
implicit none
real(8), dimension(:,:,:), allocatable :: dip, a1 ! dipolar interaction and additional
real(8), dimension(:,:), allocatable :: sx, sy, sz, sI, sp, sm, o, u, v, w, & ! spin matrices and additional
x, y, z, r, & ! r = {x, y, z}, distances between magnetic ions (MI)
J0, & ! exchange interactions
ReH, ImH, b, q, q2, & ! Hamiltonian parts and additional
d0, d1 ! for Kronecker product procedure
real(8), dimension(:), allocatable :: x1, y1, z1, & ! coordinates of MI
RT2, RT3, RT4, RT1, sum_sqr, & ! for rotation method
histp, hist ! partial and averaged histogram
logical, dimension(:), allocatable :: mask1
real(8), dimension(1:3) :: e1, e2, e3, d ! lattice basis
real(8), dimension(1) :: i11, k11
real(8) S, eps, & ! spin, precision
alpha, beta, pd, & ! parameters of exchange (A*exp(-B*r)) and dipolar interaction (pd = (hbar*gamma)^2)
res, & ! histogram resolution
s1, s2, c1, c2, & ! rotation parameters
m, e, c
integer N, N1, N2, N3, NN, Nres, & ! total number of MI and their concentration
i, j, k, i1, j1, k1, t, m3, ms, l, r1, ires, & ! counters
f, fn, & ! 2S+1, (2S+1)^N
nh ! number of histogram bars
logical noconv
!----------------------------------------------------
! read and set the initial parameters
!----------------------------------------------------
open(1, file="init.txt", form="formatted", action="read")
read(1,*) eps, S, N, N1, N2, N3, nh, alpha, beta, pd, &
e1, e2, e3, res, Nres
close(1)
f = 2*S + 1; fn = f**N
call RANDOM_SEED()
!----------------------------------------------------
! memory alloc
!----------------------------------------------------
allocate(sx(1:f,1:f)); allocate(sy(1:f,1:f)); allocate(sz(1:f,1:f))
allocate(sI(1:f,1:f)); allocate(sp(1:f,1:f)); allocate(sm(1:f,1:f))
allocate(o(1:f,1:f)); allocate(v(1:f,1:f)); allocate(w(1:f,1:f))
allocate(dip(1:6,1:N,1:N)); allocate(J0(1:N,1:N)); allocate(u(1:N,1:N))
allocate(x(1:N,1:N)); allocate(y(1:N,1:N)); allocate(z(1:N,1:N))
allocate(r(1:N,1:N))
allocate(x1(1:N)); allocate(y1(1:N)); allocate(z1(1:N))
allocate(ReH(1:fn,1:fn)); allocate(ImH(1:fn,1:fn))
allocate(b(1:fn,1:fn)); allocate(q(1:fn,1:fn)); allocate(q2(1:fn,1:fn))
allocate(mask1(1:fn))
allocate(a1(1:N,1:f,1:f))
allocate(RT1(1:fn)); allocate(RT2(1:fn))
allocate(RT3(1:fn)); allocate(RT4(1:fn))
allocate(sum_sqr(1:fn))
allocate(histp(1:nh)); allocate(hist(1:nh))
hist = 0.0d0
open(1, file="MI_coords.txt", form="formatted", action="write")
open(2,file="E.txt", form="formatted", action="write")
!----------------------------------------------------
! spin matrices initialization
!----------------------------------------------------
sx = 0.0d0; sy = 0.0d0; sz = 0.0d0; sp = 0.0d0; sm = 0.0d0; sI = 0.0d0
do i = 1, f, 1
sI(i,i) = 1.0d0
sz(i,i) = S - (i-1)
if(i <= f-1) sp(i,i+1) = dsqrt(dabs(S*(S+1.0d0) - real(i*(i+1))))
enddo
sm = transpose(sp)
sx = 0.5d0*(sp + sm)
sy = 0.5d0*(sm - sp)
!----------------------------------------------------
ires = 1
REALIZATION: do while(ires <= Nres)
!----------------------------------------------------
! generation of MI distribution in lattice
!----------------------------------------------------
x = 0.0d0; y = 0.0d0; z = 0.0d0; r = 0.0d0
COORDS: do
! MI coordinates
do i = 1, N, 1
call RANDOM_NUMBER(d)
d(1) = floor(d(1)*N1); d(2) = floor(d(2)*N2); d(3) = floor(d(3)*N3)
x1(i) = d(1)*e1(1) + d(2)*e2(1) + d(3)*e3(1)
y1(i) = d(1)*e1(2) + d(2)*e2(2) + d(3)*e3(2)
z1(i) = d(1)*e1(3) + d(2)*e2(3) + d(3)*e3(3)
enddo
! MI distances
do i = 1, N, 1
do j = 1, N, 1
if(i /= j)then
x(i,j) = x1(i) - x1(j)
y(i,j) = y1(i) - y1(j)
z(i,j) = z1(i) - z1(j)
! full interaction
r(i,j) = dsqrt( x(i,j)**2 + y(i,j)**2 + z(i,j)**2 )
endif
enddo
r(i,i) = 1.0d0
enddo
if(minval(r) > 0.5d0)exit
enddo COORDS
! write MI coordinated
write(1,'(A,I8)') "Realization ", ires
do i = 1, N, 1
write(1,'(I6, 3E20.6E3)') i, x1(i), y1(i), z1(i)
enddo
write(1,*)
!----------------------------------------------------
! pair interaction evaluation
!----------------------------------------------------
! isotropic part
J0 = alpha*dexp(-beta*r)
dip(1,:,:) = J0 + pd * (1.0d0 - 3.0d0*x**2 / r**2) / r**3
dip(2,:,:) = J0 + pd * (1.0d0 - 3.0d0*y**2 / r**2) / r**3
dip(3,:,:) = J0 + pd * (1.0d0 - 3.0d0*z**2 / r**2) / r**3
! anisotropic part
dip(4,:,:) = -3.0d0*pd*x*y / r**5
dip(5,:,:) = -3.0d0*pd*x*z / r**5
dip(6,:,:) = -3.0d0*pd*y*z / r**5
!----------------------------------------------------
! real part of the Hamiltonian matrix
!----------------------------------------------------
o = sz; call p78()
ReH = b
u = dip(1,:,:); v = sx; w = sx; call p56()
u = dip(2,:,:); v = sy; w = -sy; call p56()
u = dip(3,:,:); v = sz; w = sz; call p56()
u = dip(5,:,:); v = sx; w = sz; call p56()
q = ReH; ReH = 0.0d0
!----------------------------------------------------
! imaginary part of the Hamiltonian matrix
!----------------------------------------------------
u = dip(4,:,:); v = sx; w = sy; call p56()
u = dip(6,:,:); v = sy; w = sz; call p56()
ImH = ReH; ReH = q
!----------------------------------------------------
! Diagonalization of the Hamiltonian matrix
!----------------------------------------------------
t = 0; q = 0.0d0; q2 = 0.0d0
do i = 1, fn, 1
q(i,i) = 1.0d0
enddo
! sum of squares by strings
sum_sqr = 0.0d0
do i = 1, fn, 1
do j = 1, fn, 1
if(i /= j) sum_sqr(i) = sum_sqr(i) + (ReH(i,j)**2 + ImH(i,j)**2)
enddo
enddo
noconv = .false.
! rotation iterations
ROTATION: do
i11 = maxloc(sum_sqr); i1 = i11(1)
mask1 = .true.; mask1(i1) = .false.
k11 = maxloc(ReH(i1,:)**2 + ImH(i1,:)**2, mask=mask1); k1 = k11(1)
m = maxval(ReH(i1,:)**2 + ImH(i1,:)**2, mask=mask1)
if(m < eps)exit
if(t == 100000)then
noconv = .true.
exit
endif
mask1(k1) = .false.
sum_sqr = sum_sqr - sum(ReH(:,i1)**2 + ImH(:,i1)**2, mask=mask1)
i = i1; k = k1
! rotation parameters
e = dabs(ReH(i,i) - ReH(k,k)) / dsqrt( (ReH(i,i) - ReH(k,k))**2 + 4.0d0*(ReH(i,k)**2 + ImH(i,k)**2) )
s1 = dsqrt( 0.5d0*(1.0d0 - e) ); c1 = dsqrt( 0.5d0*(1.0d0 + e) )
if(ReH(i,i) /= ReH(k,k)) s1 = sign(s1, ReH(i,i) - ReH(k,k))
if(ReH(i,k) /= 0.0d0) s1 = sign(s1, ReH(i,k))
s2 = ImH(i,k) / dsqrt(ReH(i,k)**2 + ImH(i,k)**2)
if(ReH(i,k) /= 0.0d0) s2 = sign(s2, ReH(i,k))
c2 = s1 * dabs(ReH(i,k)) / dsqrt(ReH(i,k)**2 + ImH(i,k)**2)
s1 = s1*s2
! make the rotations
RT1 = c1*q(:,i) + c2*q(:,k) + s1*q2(:,k)
RT2 = -c2*q(:,i) + c1*q(:,k) + s1*q2(:,i)
RT3 = -s1*q(:,k) + c1*q2(:,i) + c2*q2(:,k)
RT4 = -s1*q(:,i) - c2*q2(:,i) + c1*q2(:,k)
q(:,i) = RT1; q(:,k) = RT2; q2(:,i) = RT3; q2(:,k) = RT4
RT1 = c1*ReH(:,i) + c2*ReH(:,k) + s1*ImH(:,k)
RT2 = -c2*ReH(:,i) + c1*ReH(:,k) + s1*ImH(:,i)
RT3 = -s1*ReH(:,k) + c1*ImH(:,i) + c2*ImH(:,k)
RT4 = -s1*ReH(:,i) - c2*ImH(:,i) + c1*ImH(:,k)
ReH(:,i) = RT1; ReH(:,k) = RT2; ImH(:,i) = RT3; ImH(:,k) = RT4
RT1 = c1*ReH(i,:) + c2*ReH(k,:) - s1*ImH(k,:)
RT2 = -c2*ReH(i,:) + c1*ReH(k,:) - s1*ImH(i,:)
RT3 = c1*ImH(i,:) + c2*ImH(k,:) + s1*ReH(k,:)
RT4 = -c2*ImH(i,:) + c1*ImH(k,:) + s1*ReH(i,:)
ReH(i,:) = RT1; ReH(k,:) = RT2; ImH(i,:) = RT3; ImH(k,:) = RT4
t = t+1
mask1 = .true.; mask1(i1) = .false.; mask1(k1) = .false.
sum_sqr = sum_sqr + sum(ReH(:,i1)**2 + ImH(:,i1)**2, mask = mask1) &
+ sum(ReH(:,k1)**2 + ImH(:,k1)**2, mask = mask1)
mask1 = .true.; mask1(i1) = .false.
sum_sqr(i1) = sum(ReH(i1,:)**2 + ImH(i1,:)**2, mask = mask1)
mask1 = .true.; mask1(k1) = .false.
sum_sqr(k1) = sum(ReH(k1,:)**2 + ImH(k1,:)**2, mask = mask1)
enddo ROTATION
!----------------------------------------------------
if(noconv)then
print *, "Realization does not converge"
else
print *,ires, ", Rotation finished at ", t, " iterations"
!----------------------------------------------------
! eigenvalues
!----------------------------------------------------
do i = 1, fn, 1
RT1(i) = ReH(i,i)
enddo
! write energy
write(2,'(A,I8)') "Realization ", ires
do i = 1, fn, 1
write(2,'(I6,E20.6E3)') i, RT1(i)
enddo
write(2,*)
!----------------------------------------------------
! evaluate probabilities and histogram amplitudes
!----------------------------------------------------
histp = 0.0d0
o = sx
call p78()
ReH = matmul(b, q); ImH = matmul(b, q2)
d1 = transpose(q); b = transpose(q2)
q = matmul(d1, ReH) + matmul(b, ImH)
q2 = matmul(d1, ImH) - matmul(b, ReH)
do i = 1, fn, 1
do j = 1, fn, 1
c = q(i,j)**2 + q2(i,j)**2
k = floor(1.0d0 + dabs(RT1(i) - RT1(j)) / res)
if(k <= nh) histp(k) = histp(k) + c
enddo
enddo
hist = hist + histp
ires = ires + 1
endif
enddo REALIZATION
!----------------------------------------------------
open(3,file="hist.txt", form="formatted", action="write")
do i = 1, nh, 1
write(3,'(2E20.6E3)') i*res, hist(i) / Nres
enddo
close(1); close(2); close(3)
print *,"Histogram is written at hist.txt"
!----------------------------------------------------
! memory clear
!----------------------------------------------------
deallocate(sx); deallocate(sy); deallocate(sz); deallocate(sI)
deallocate(o); deallocate(v); deallocate(w)
deallocate(ReH); deallocate(ImH); deallocate(b); deallocate(q); deallocate(q2)
deallocate(mask1); deallocate(a1)
deallocate(RT1); deallocate(RT2); deallocate(RT3); deallocate(RT4); deallocate(sum_sqr)
deallocate(histp); deallocate(hist)
deallocate(dip); deallocate(J0); deallocate(sp); deallocate(sm)
deallocate(x1); deallocate(y1); deallocate(z1)
deallocate(x); deallocate(y); deallocate(z); deallocate(r); deallocate(d1)
contains
!----------------------------------------------------
! Kronecker product of one spin and N-1 identity
!----------------------------------------------------
subroutine p78()
b = 0.0d0
do k = 1, N, 1
a1(k,:,:) = sI
enddo
do k = 1, N, 1
a1(k,:,:) = o
call p34()
a1(k,:,:) = sI
b = b + d1
enddo
end subroutine p78
!----------------------------------------------------
! Kronecker product of two spin and N-2 identity
!----------------------------------------------------
subroutine p56()
do k = 1, N, 1
do t = 1, N, 1
if(k /= t)then
a1(k,:,:) = v; a1(t,:,:) = w
endif
call p34()
a1(k,:,:) = sI; a1(t,:,:) = sI
ReH = ReH + u(k,t)*d1
enddo
enddo
end subroutine p56
!----------------------------------------------------
! Kronecker product of N matrices
!----------------------------------------------------
subroutine p34()
if(allocated(d0)) deallocate(d0)
if(allocated(d1)) deallocate(d1)
allocate(d0(1:f,1:f)); d0 = 0.0d0
allocate(d1(1:f**2,1:f**2)); d1 = 0.0d0
d0 = a1(1,:,:)
do m3 = 2, N, 1
NN = f**(m3-1)
do i = 1, NN, 1
do j = 1, NN, 1
do ms = 1, f, 1
do l = 1, f, 1
r1 = (i-1)*f + ms; i1 = (j-1)*f + l
d1(r1,i1) = d0(i,j)*a1(m3,ms,l)
enddo
enddo
enddo
enddo
if(m3 < N)then
deallocate(d0); allocate(d0(1:f**m3,1:f**m3)); d0 = 0.0d0
d0 = d1
deallocate(d1); allocate(d1(1:f**(m3+1),1:f**(m3+1))); d1 = 0.0d0
endif
enddo
deallocate(d0)
end subroutine p34
end program NMR_rarefiedПростите, без подсветки, хабраредактор всё-таки современен
