Факторный анализ для чайников
Думаю многие из нас, хотя бы однажды интересовались искусственным интеллектом и нейронными сетями. В теории нейронных сетей далеко не последнее место занимает факторный анализ. Он призван выделить так называемые скрытые факторы. У этого анализа есть много методов. Особняком стоит метод главных компонент, отличительной особенностью которого является полное математическое обоснование. Признаться честно, когда я начал читать статьи по приведенным выше ссылкам — стало не по себе от того, что я ничего не понимал. Мой интерес поутих, но, как это обычно бывает, понимание пришло само по себе, нежданно-негаданно.Итак, давайте рассмотрим арабские цифры от 0 до 9. В данном случае формата 5×7, которые брались из проекта под LCD от Nokia 3310.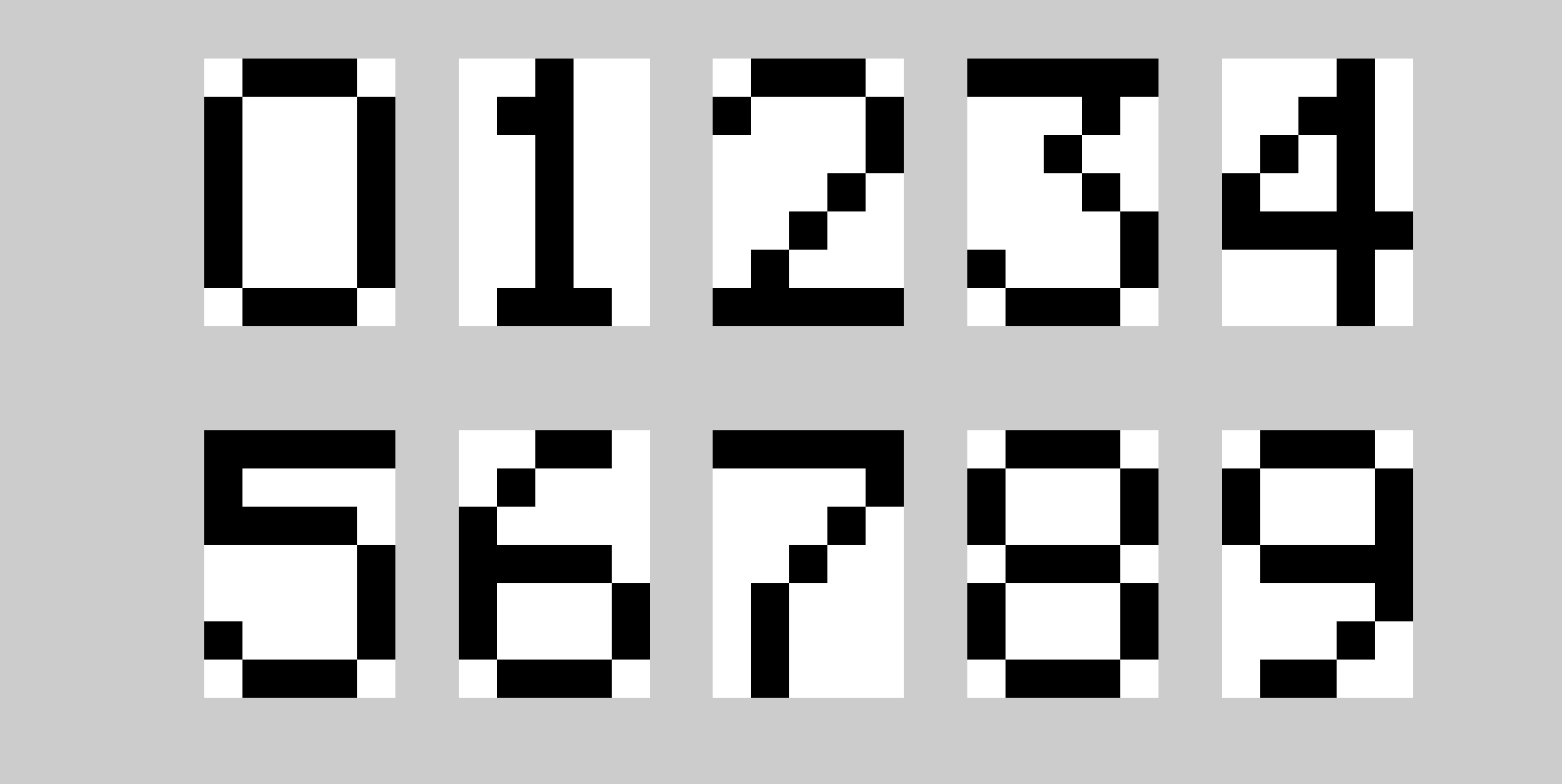
Черным пикселям соответствует 1, белым — 0. Таким образом, каждую цифру мы можем представить в виде матрицы 5×7. Например матрица ниже: 
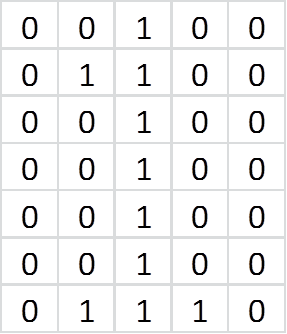соответствует картинке: 
Давайте просуммируем картинки для всех цифр, а результирующую нормируем. Это означает получить матрицу 5×7, ячейки которых содержат сумму тех же ячеек для разных цифр деленных на их количество. В итоге мы получим картинку: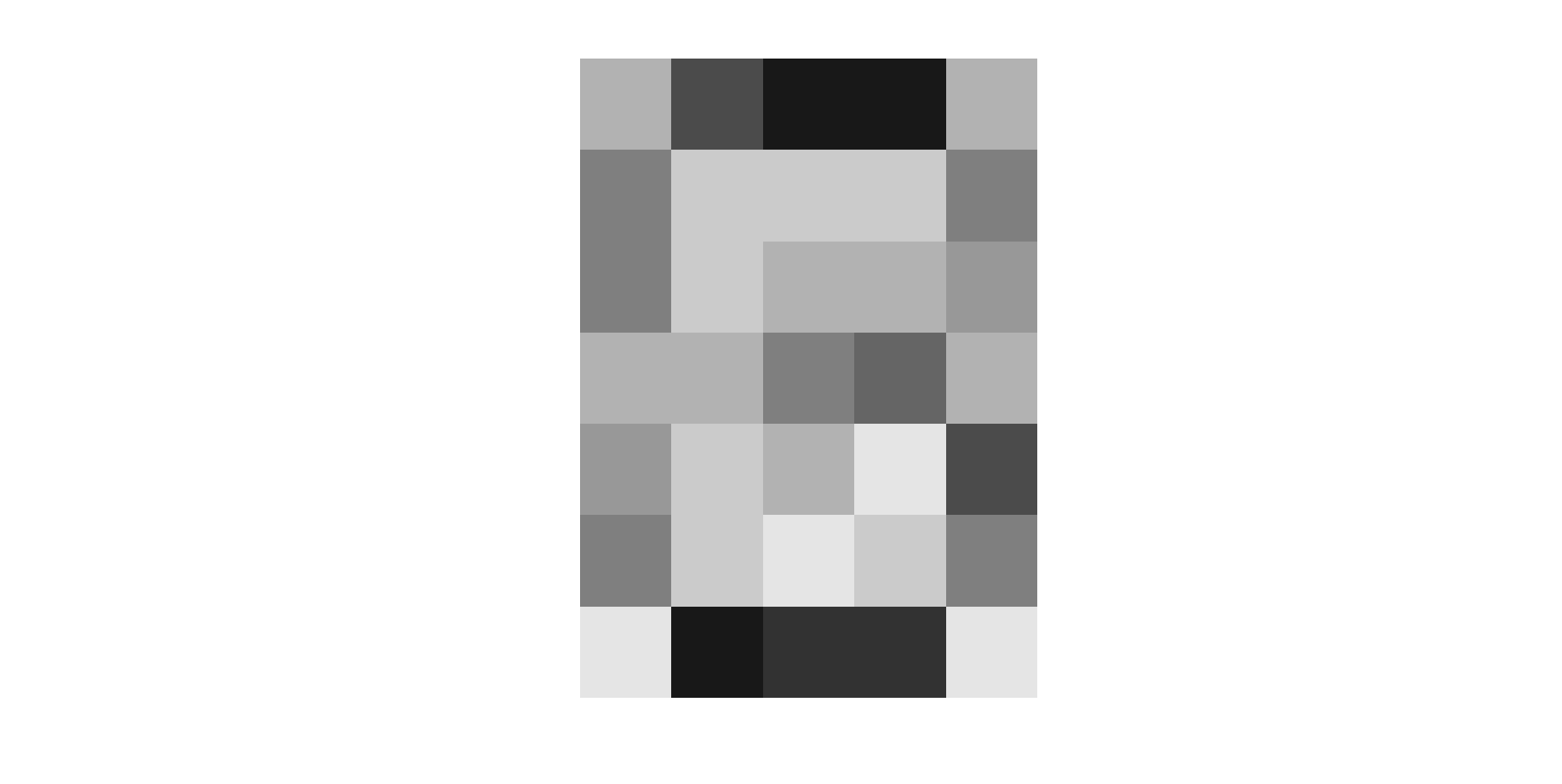 
Матрица для нее: 
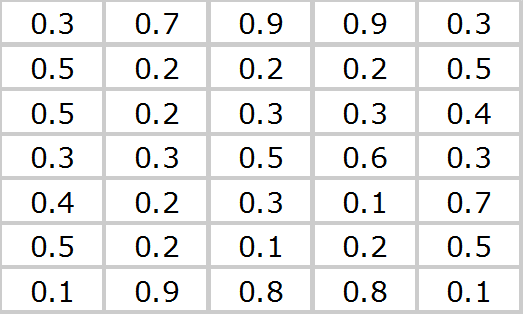В глаза сразу бросаются самые темные участки. Их три, и соответствуют они значению 0.9. Это то чем они похожи. То что общее для всех цифр. Вероятность встретить черный пиксель в этих местах высокая. Давайте рассмотрим самые светлые участки. Их также три, и соответствуют они значению 0.1. Но опять-таки это то, чем все цифры похожи, что общее для них всех. Вероятность встретить белый пиксель в этих местах высокая. Чем же они различаются? А максимум различия между ними в местах со значением 0.5. Цвет пикселя в этих местах равновероятен. Половина цифр в этих местах будут черными, половина — белыми. Давайте проанализируем эти места, благо у нас их всего 6.
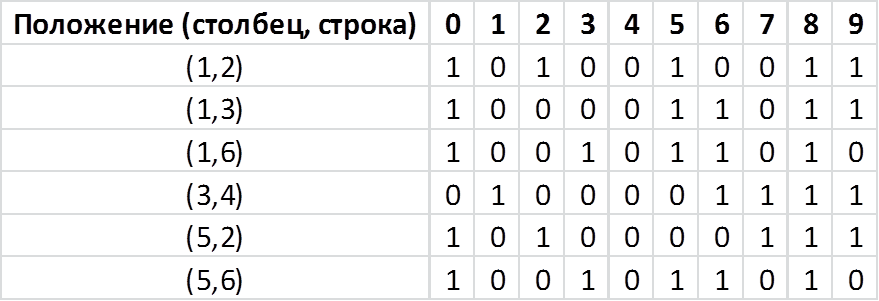Положение пикселя определенно столбцом и строкой. Отсчет начинается с 1, направление для строки сверху-вниз, для столбца слева-направо. В остальных ячейках вбито значение пикселя для каждой цифры в заданном положении. Теперь давайте отберем минимальное количество положений, при которых мы все еще сможем различать цифры. Иными словами, для которых значения в столбцах будут различны. Так как цифр у нас 10, а кодируем мы их двоично, математически необходимо как минимум 4 комбинации 0 и 1 (log (10)/log (2)=3.3). Давайте попробуем из 6 отобрать 4 которые удовлетворяли бы нашему условию: 
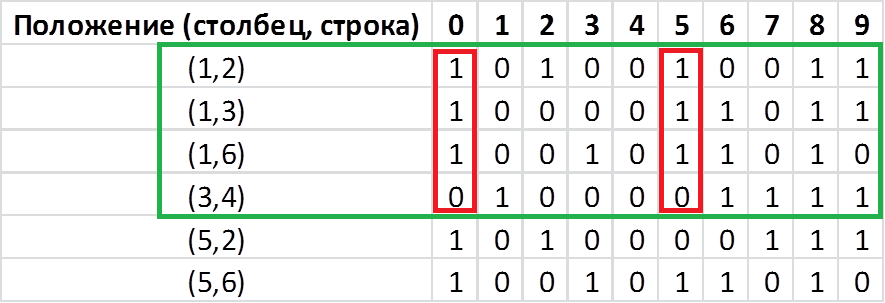Как видим значение в столбцах 0 и 5 совпадают. Рассмотрим другую комбинацию: 
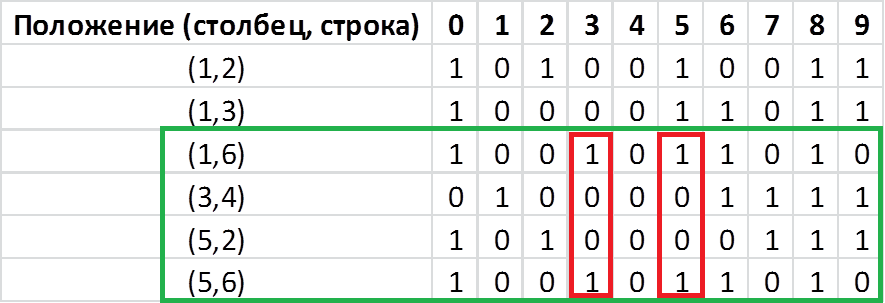Тут также есть совпадения между 3 и 5 столбцами. Рассмотрим следующую: 
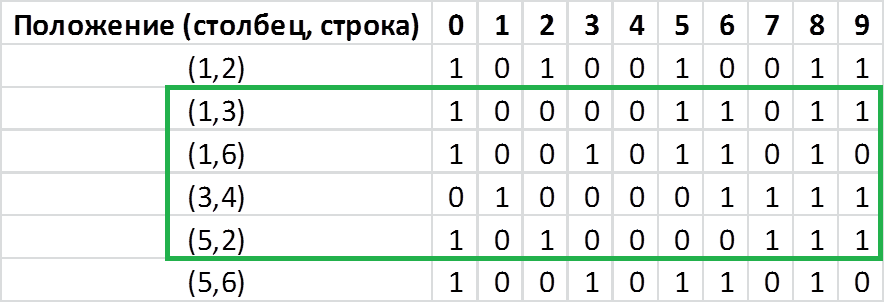А вот здесь никаких коллизий. Бинго! А теперь я расскажу вам для чего все это затевалось: 
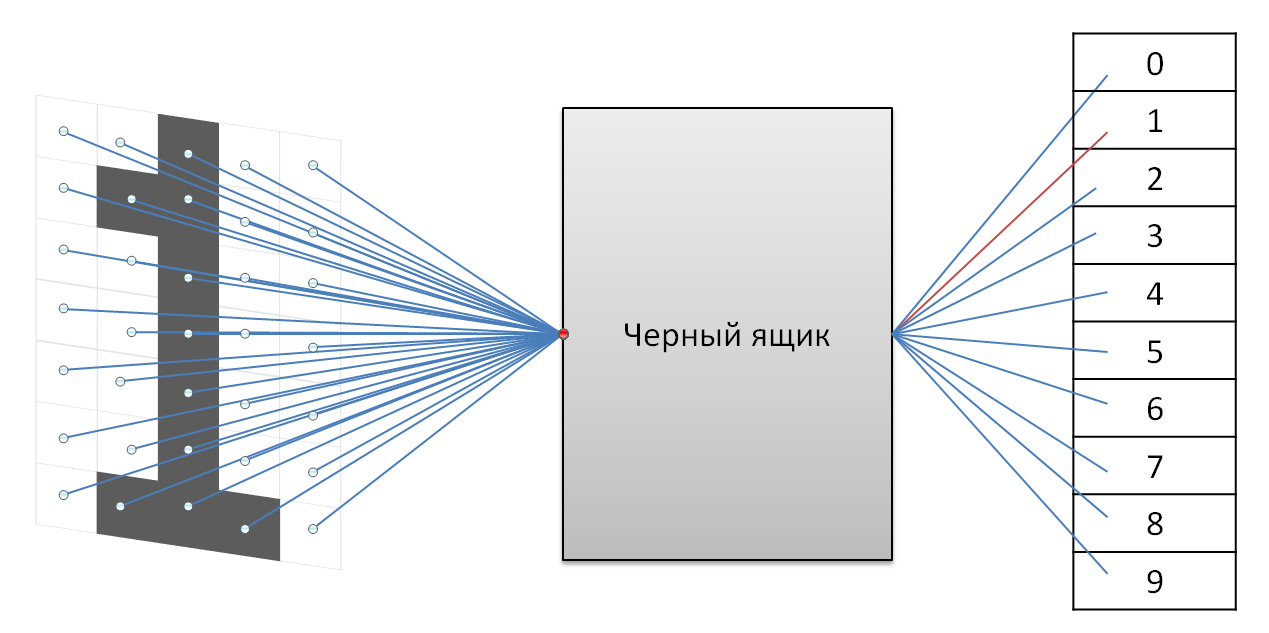Предположим с каждого пикселя, коих у нас 5×7=35, сигнал входит в некий черный ящик, а на выходе — сигнал, который соответствует входной цифре. А что происходит в черном ящике? А в черном ящике из всех 35 сигналов выбираются те 4, которые подаются на вход дешифратора и позволяют однозначно определить цифру на входе. Теперь понятно для чего мы искали комбинации без совпадений. Ведь если бы в черном ящике выбирались 4 сигнала первой комбинации, то цифры 0 и 5 для такой системы были бы попросту не различимы. Мы минимизировали задачу, ведь вместо 35 сигналов достаточно обработать лишь 4. Те 4 пикселя и являются минимальным набором скрытых факторов, которые характеризуют данный массив цифр. Очень интересную особенность имеет этот набор. Если присмотреться к значениям в столбцах, можно заметить что цифра 8 противоположность цифре 4, 7 — 5, 9 — 3, 6 — 2, а 0 — 1. Внимательный читатель спросит, а причем тут нейронные сети? А особенностью нейронных сетей является то что она сама способна выделить эти факторы, без вмешательства разумного человека. Ты просто периодически показываешь ей цифры, а она находит те 4 скрытых сигнала и коммутирует его с одним из 10 своих выходов. Как можно применить те похожие сигналы, которые мы обговаривали вначале? А они могут служить меткой набора цифр. К примеру римские цифры будут иметь свой набор максимумов и минимумов, а буквы — свой. По сигналам схожести ты сможешь отделить цифры от букв, но распознать символы внутри набора возможно только по максимальному различию.
