Алгоритм поиска «одинаковых» геометрий
Привет! Меня зовут Мацкевич Евгений, я бекэнд-разработчик 3D-движка компании «Бимейстер». Хоть это и не очевидно на первый взгляд, но элементы загружаемых пользователями 3D-моделей зачастую повторяются, имея при этом различные положение в пространстве, масштабирование и вращение. Я расскажу о том, как мы научили нашу систему распознавать такие элементы как «одинаковые», выделять из них уникальный, а для остальных — вычислять матрицы трансформации. Это дало возможность однократно загружать уникальный элемент, а вместо прочих одинаковых — их матрицы, что сократило трафик и объем занимаемой оперативной памяти.
В рамках форматов 3D-моделей, создаваемых с использованием тех или иных САПРов, элементы могут быть заданы разными способами (набором вершин и нормалей, B-rep, или, в общем случае, параметрически). Поэтому сперва, на этапе парсинга, все элементы 3D-моделей приводятся к единому виду — набору вершин и нормалей (далее геометрия). Это дает возможность применять алгоритм поиска одинаковых геометрий.
Итак, геометрия задается набором вершин и нормалей. Но нормалями в данном случае будем пренебрегать. Каждые три вершины образуют треугольник. Эти треугольники, соединяясь вместе, образуют поверхность геометрической фигуры. Для того, чтобы задать куб, нужно двадцать четыре вершины, а не восемь, поскольку куб состоит из шести граней, а каждая грань — из двух треугольников (Рисунок 1).
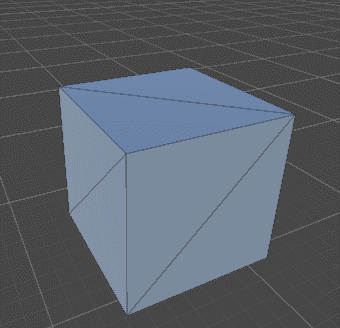Рисунок 1. Изображение куба
Условия, при которых мы будем считать две геометрии одинаковыми:
Одинаковые дескрипторы;
Существует такая матрица трансформации, применив которую к каждой вершине первой геометрии, получим набор вершин, идентичный набору вершин второй геометрии. Порядок вершин значения не имеет.
Дескрипторы
В общем виде дескриптором является некоторая характеристика, описывающая геометрию (прочитать подробно можно на medium.com). Мы будем пользоваться дескриптором, инвариантным к вращению, перемещению и масштабированию по трем осям пропорционально.
Метод расчета дескриптора:
Найдем центр масс геометрии. Это среднее арифметическое всех вершин.
Получим геометрию в локальной системе координат. Вычтем из каждой вершины центр масс.
Получим нормализованную геометрию. Впишем геометрию в сферу единичного радиуса с центром в начале координат.
Составим массив длин векторов нормализованной геометрии, упорядоченный по возрастанию. Это должен быть массив чисел от нуля до единицы.
Округлим числа до заданной точности (в нашем случае это 4 знака после запятой) и рассчитаем хэш-значение от полученных чисел (алгоритм хэширования MD5). Полученная величина и будет дескриптором.
Таким образом, приведение к локальной системе координат нивелирует компоненту перемещения, нормализация — масштабирования, а сортировка массива длин — вращения.
Расчет дескрипторов относительно «дешев» и позволяет сгруппировать потенциально одинаковые геометрии, сокращая размер выборки для последующего вычисления матрицы трансформации.
Равенство дескрипторов является необходимым, но
недостаточным условием, при котором геометрии будут считаться одинаковыми.
Вычисление матрицы трансформации
Матрица трансформации состоит из трех компонентов:
Перемещение;
Масштабирование;
Вращение.
Перемещение и масштабирование были получены в ходе расчета дескриптора. С нахождением вращения все гораздо сложнее.
Алгоритм вычисления вращения по двум парам векторов
Представим все вершины геометрии как вектора с основанием в начале координат. Для того, чтобы найти вращение от первой геометрии ко второй, нужно найти вращение любой пары векторов из первой геометрии к точно такой же паре из второй. Для этого выберем две произвольные вершины из первой геометрии (Анимация 1).
Анимация 1. Две произвольные вершины u0 и v0 из первой геометрии
Далее найдем пару вершин из второй геометрии так, чтобы длины векторов и угол были равны длинам и углу первой пары. Пар векторов с такими параметрами во второй геометрии может быть сколь угодно много, и для них придется делать перебор, пока не найдется действительно нужное вращение. Поэтому пару векторов лучше подобрать так, чтобы других пар с такими параметрами было как можно меньше.
Пусть (Рисунок 2):
Рисунок 2. Две пары векторов
Тогда мы ищем вращение q, которое преобразует u0 в u2, а v0 в v2(Анимация 2):
Анимация 2. Вращение q
Для этого разложим q на два последовательных вращения q1 и q2:
q1 = u0 → u1;
q1 = v0 → v1;
q2 = u1 → u2;
q2 = v1 → v2.
Таких комбинаций из двух вращений может быть бесконечное множество.
Выберем такое множество вращений q1, при котором u0 = u1, т.е. это вращения вокруг оси u0(Анимация 3).
Анимация 3. Множество вращений вокруг оси u0
Тогда вращение q2 преобразует u0 в u2:
q2 = u0 → u2.
Для вычисления кватерниона q2 нам достаточно вычислить угол между u0 и u2, а в качестве оси вращения выберем Nu — нормаль к плоскости, в которой лежат векторы u0 и u2(Анимация 4).
Анимация 4. Вращение q2 вокруг оси Nu
Осталось определить q1.
Известно, что q2 преобразует v1 в v2, тогда обратное вращение q2* (конъюгат кватерниона) преобразует v2 в v1 (Анимация 5). Отсюда мы можем найти v1.
Анимация 5. Вращение q2* вокруг оси Nu
О q1 верно следующее:
q1 — вращение вокруг оси u0.
q1 = v0 → v1;
Мы могли бы найти вращение q1, аналогично q2 по углу между v0 в v1, и оси u0, но ось u0 не обязательно будет являться нормалью к плоскости, в которой лежат v0 и v1. Поэтому найдем проекции v0 и v1 на плоскость, ортогональную оси u0. Назовем их v'0 и v'1(Рисунок 3).
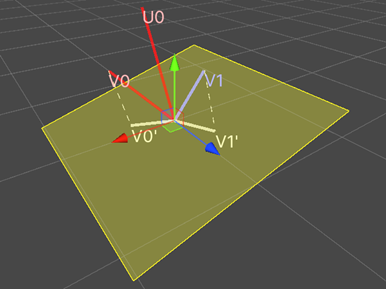Рисунок 3. Проекции v'0 и v'1
Вращение q1 вокруг оси u0, которое преобразует v0 в v1, также преобразует и v'0 в v'1.
Найдем q1, используя угол между v'0 и v'1 и ось u0 (Анимация 6).
Анимация 6. Вращение q1 вокруг оси u0
Конечное вращение получим, перемножив кватернионы q = q2 * q1. Выглядеть оно будет как на анимации 2.
Итак, повернем первую геометрию, используя вычисленное вращение, и сравним ее повершинно со второй геометрией. Если обнаружится хоть одна пара неравных вершин, то, несмотря на рассчитанное вращение, одинаковыми такие геометрии являться не будут. Это означает, что пары векторов были выбраны неверно, и требуется повторить поиск вращения со следующей парой.
Далее, имея вычисленные значения перемещения, масштабирования и вращения, мы можем найти итоговую матрицу трансформации.
Назначение и нюансы применения алгоритма
Подчеркнем, что вышеописанный алгоритм прекрасно справляется с поиском одинаковых геометрий, имеющих равное количество вершин. Он не подходит для поиска похожих по строению геометрий или геометрий разной степени полигональности.
В дополнение хотелось бы отметить некоторые нюансы алгоритма поиска одинаковых геометрий:
От метода вычисления дескриптора зависит качество работы алгоритма в целом.
Алгоритм расчета дескриптора может давать как ложноположительный, так и ложноотрицательный результат. Если результат ложноположительный, т.е. две геометрии имеют одинаковое значение дескриптора, но «одинаковыми» при этом не являются, то, получается, что мы зря ищем вращение. Однако, в случае ложноотрицательного результата и вовсе упускается возможность применения алгоритма поиска вращения для заведомо одинаковых геометрий.
Сравнение вершин, как и вычисление дескриптора, должны выполняться с некоторой заданной точностью, т.к. мы имеем дело с числами с плавающей запятой.
