[Перевод] Откуда берётся квантовая неопределённость?04.10.2022 00:01

Даже такой простой объект, как атом, проявляет квантовую неопределённость. Если спросить, «где отдельный электрон находится прямо сейчас?», ответ можно дать лишь с определённой, ограниченной точностью.

Как бы мы ни совершенствовали своё измерительное оборудование, отдельные квантовые свойства остаются в известной мере неопределёнными. Догадываетесь, почему? Подробности — к старту нашего флагманского курса по Data Science.

Возможно, самое странное открытие человечества состоит в том, что наша физическая реальность управляется не только детерминированными [чётко определёнными] законами. На фундаментальном, то есть квантовом, уровне законы физики становятся вероятностными: можно вычислить вероятность возможных экспериментальных результатов, но, только измеряя рассматриваемую величину, вы действительно можете определить, что делает данная система в данный момент. Более того, сам акт измерения или наблюдения определённых величин приводит к росту неопределённости связанных с ними свойств. Физики называют это сопряжёнными переменными.

Многие люди полагают, что неопределённость и индетерминизм — мнимые понятия, которые возникли лишь из-за «скрытых» детерминированных параметров. Тем не менее механизм прогнозирования квантовых результатов нам ещё только предстоит открыть. Однако, может быть, всему виной существующие в пространстве квантовые поля? На этой неделе Пол Мариначчо задал такой вопрос:

«Мне уже давно интересно: это квантовый вакуум обеспечивает колебания волновых пакетов частиц? Действует ли он так… как, по мнению людей, действует эфир? Я знаю, что это очень упрощённый вопрос, но затрудняюсь выразить его в терминах математики».

Давайте послушаем, что об этом думает Вселенная. Поехали!

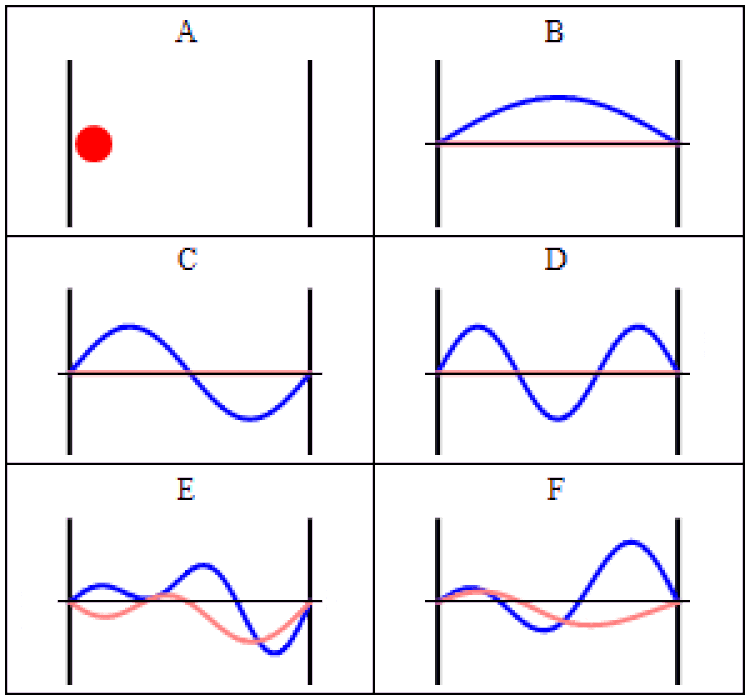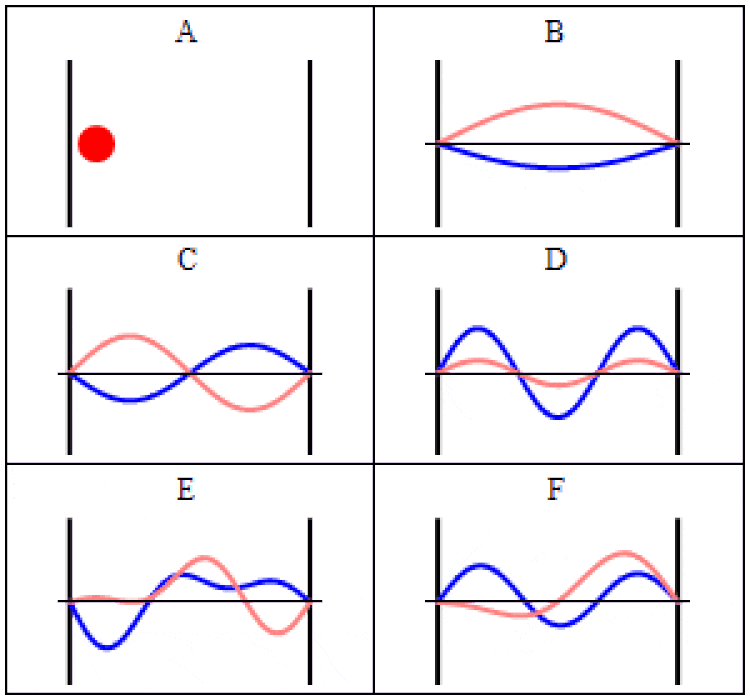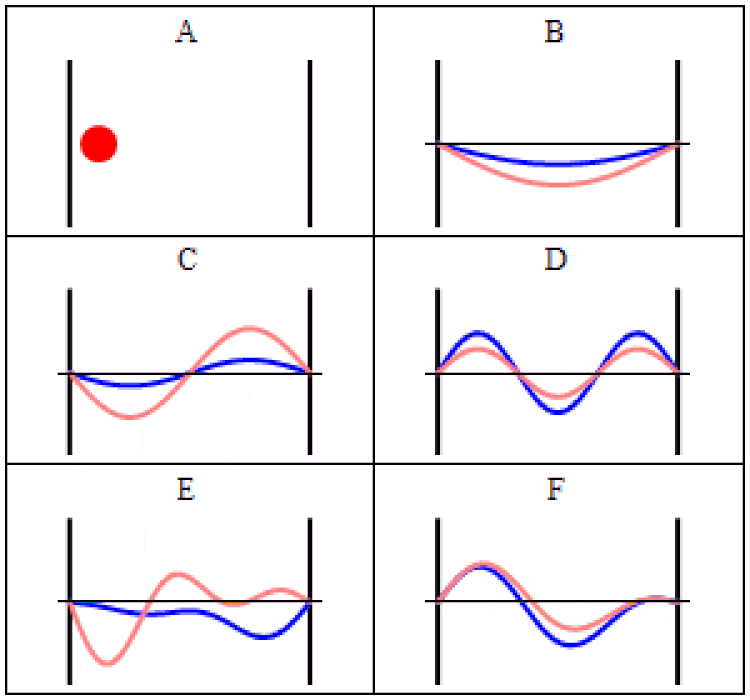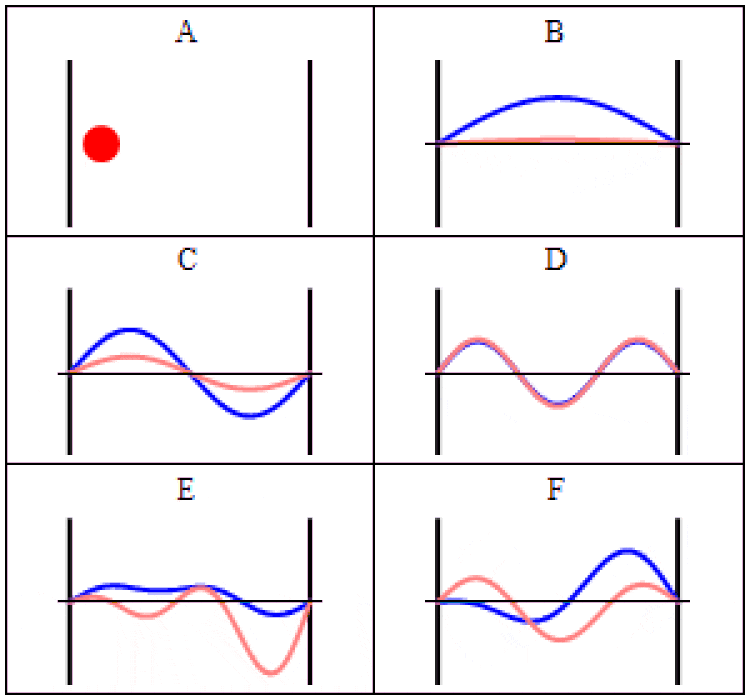
Траектории движения частицы в «ящике» (она же — бесконечная прямоугольная потенциальная яма) в классической (A) и квантовой механике (B-F). В случае (A) частица движется с постоянной скоростью, отскакивая вперёд и назад. В случае (B-F) волновые функции, которые являются решениями время-зависимого уравнения Шрёдингера, показаны при одинаковых геометрии и потенциале. В том, где будет находиться эта частица в любой момент, есть неопределённость. Эта неопределённость присуща квантовым законам, которые управляют Вселенной, но никак не объясняется ими. (Автор (ы): Steve Byrnes via Mathematica; Sbyrnes321/Wikimedia Commons)

В квантовой физике есть два представления о неопределённости. Одно из них звучит так: «Я создал систему с заданными свойствами, что я смогу сказать об этих свойствах, если вернусь к ней через какое-то время?» Некоторые свойства — такие как масса стабильной частицы, электрический заряд частицы, энергетический уровень электрона, связанного в основном состоянии атома, и т. д. — останутся неизменными. До тех пор, пока между квантовой частицей и её окружением не будет новых взаимодействий, эти свойства будут чётко попадать в область известного, без всякой неопределённости.

С остальными свойствами ясности меньше. Поместите свободный электрон в пространство в точно известном положении, а когда вы вернётесь чуть позже, положение электрона уже не будет вам точно известно: волновая функция, которая описывает его положение, растянута во времени. Если вы хотите узнать, распалась ли нестабильная частица, вы можете узнать это, только измерив свойства этой частицы. Если же вы спросите, какова была масса нестабильной частицы до радиоактивного распада, восстановить эту информацию можно, измерив энергию и импульс каждой из частиц, на которые она распалась. Однако от события к событию результаты будут различаться. Они будут неопределёнными и зависящими от времени существования частицы.

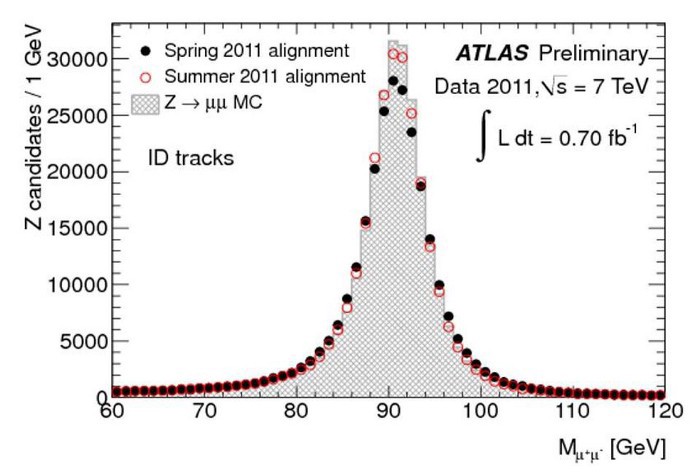
Измеренная собственная ширина, или половина ширины пика на этом изображении на полпути к максимуму, составляет 2,5 ГэВ: внутренняя неопределённость составляет около ± 3% от общей массы. Масса рассматриваемой частицы, Z-бозона, достигает пика при 91,187 ГэВ. Однако изначально эта масса в значительной степени неопределённа из-за слишком короткого времени существования. (Автор (ы): J. Schieck for the ATLAS Collaboration, JINST7, 2012

Эта квантовая неопределённость, которая возникает из-за эволюции времени, приводит к тому, что определённые свойства могут быть известны только с определённой точностью. С течением времени эта неопределённость распространяется в будущее, приводя к физическому состоянию, которое не может стать известным по нашему желанию.

У неопределённости может быть иное происхождение. Некоторые пары характеристик — сопряжённые переменные — связаны между собой таким образом, что, чем точнее измеряется одна характеристика частицы, тем менее точно можно измерить вторую. Это прямое следствие принципа неопределённости Гейзенберга даёт о себе знать в самых разных ситуациях.

Самый популярный пример связан с положением и импульсом. Чем точнее вы измерите положение частицы, тем меньше у вас возможности узнать её импульс: какими скоростью и направлением обладает её «количество движения». Подумайте о том, как производится измерение положения, и вы согласитесь с этим. Измеряется оно через квантовое взаимодействие между измеряемой частицей и другим квантом, имеющим или не имеющим массу покоя. В любом случае частице может быть присвоена длина волны, причём частицы с большей энергией имеют меньшие длины волн, а значит, позволяют точнее определить положение.

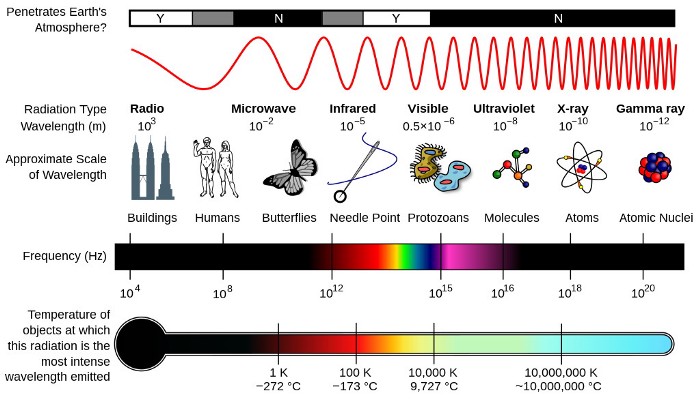
Шкалы размера, длины волны и температуры/энергии соответствуют разным частям электромагнитного спектра. Для измерения самых маленьких размеров нужно перейти в область более высоких энергий и более коротких волн. На самых больших шкалах длин волн для кодирования большого количества информации требуется очень небольшое количество энергии. Даже частицы материи имеют длину волны, зависящую от их энергии, поскольку квантовая природа существования наделяет частицы длиной волны де Бройля. Она и позволяет исследовать структуру в разных масштабах. (Автор (ы)s: NASA and Inductiveload/Wikimedia Commons)

Но, если стимулировать квантовую частицу и заставить её взаимодействовать с другой квантовой частицей, они обменяются импульсами. И, чем больше энергия взаимодействующей частицы, тем короче её длина волны. Это даёт нам больше знаний о её положении в пространстве. Но энергии и момента нам придётся передать частице больше, и это приведёт нас к большей неопределённости импульса частицы.

Вы решили, что сможете «перехитрить» эти обстоятельства? Например, измерить импульс вылетающей частицы, по которому определите её положение. Увы, это не поможет.

Некоторая неопределённость сохраняется всегда: произведение неопределённости на каждую из двух величин всегда должно быть большим или равным некоторому значению. Как бы хорошо вы ни измерили положение (Δx) и/или импульс (Δp) каждой взаимодействующей частицы, произведение неопределённости (ΔxΔp) всегда будет больше приведённой постоянной Планка, ħ/2, или будет равно половине этой постоянной.

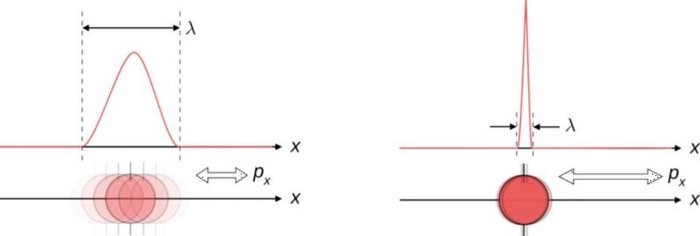
На этом рисунке — неопределённость между положением и импульсом. Когда одно известно более точно, другое удаётся определить менее точно. Каждый раз, когда вы точно измеряете одну из величин, это увеличивает неопределённость в определении другой величины. (Автор (ы): Maschen/Wikimedia Commons)

Помимо положения и импульса есть много величин, в которых выражается неопределённость. Среди них:

• ориентация и угловой момент,
• энергия и время,
• спины частицы во взаимно перпендикулярных направлениях,
• электрический потенциал и свободный электрический заряд,
• магнитный потенциал и свободный ток
• и многое другое.

Мы живём в квантовой Вселенной, поэтому возникает вопрос о том, не прячется ли за всем этим «квантовым безумием» какой-то скрытый параметр? Наконец, многие философствуют о том, присуща ли неопределённость квантовым представлениям и неизбежна ли она, то есть является ли неотъемлемым свойством природы, или же есть некая первопричина, которую мы просто не смогли выявить. Последнему из этих утверждений на протяжении всей истории отдавали предпочтение многие великие умы (включая Эйнштейна). Этот подход широко известен как теория скрытых параметров.

Это представление художника о пространственно-временной пене с крошечными пузырьками, в квадриллионы раз меньшими, чем ядро атома. Эти непрерывные колебания продолжаются лишь ничтожные доли секунды. Тому, насколько малыми они могут быть, чтобы не разрушить физику, тоже есть предел. Этот предел — масштаб Планка. Этот масштаб соответствует расстояниям порядка 10–35 м и времени порядка 10–43 с. (Автор (ы): NASA/CXC/M. Weiss)

Мне нравится представлять скрытые параметры так: Вселенная и все её частицы находятся на пластине, быстро и хаотично вибрирующей на минимальную амплитуду. Если смотреть на Вселенную в макроскопическом масштабе, эффекты этой вибрации совершенно не видны и кажется, что «фон» Вселенной, на котором существуют все её частицы, стабилен, постоянен и лишён колебаний.

Но стоит выбрать масштаб меньше — и вы замечаете присутствие всех этих квантовых свойств. Количественные параметры флуктуируют, ничто не остаётся абсолютно стабильным и неизменным с течением времени, и, чем настойчивее вы пытаетесь определить какую-либо одну из характеристик, тем большую неопределённость обнаружите в характеристике, сопряжённой с ней.

Исходя из того, что квантовые поля пронизывают всё пространство, даже абсолютно пустое, можно легко представить, что именно эти поля являются источником всего. Возможно, неопределённость, которую мы наблюдаем, возникает вследствие квантового вакуума.

Даже в вакууме пустого пространства, где нет массы, заряда, искривлений пространства и любых внешних полей, действуют законы природы и квантовые поля. И, если вы рассчитаете самое низкоэнергетическое состояние, оно и там не будет равно нулю. Энергия нулевых колебаний (или вакуума) Вселенной окажется положительной и конечной, хотя и очень маленькой величиной. (Автор (ы): Derek Leinweber)

Это явно не та идея, которую легко списать со счетов. Факт квантовой неопределённости «заложен» в наше фундаментальное понимание частиц и полей. Каждая (работающая) формулировка квантовой механики и теории квантового поля содержит её, причём на фундаментальном уровне, а не просто ситуативно и не постфактум. На самом деле мы даже не знаем, как использовать теорию квантового поля при расчёте общего вклада в квантовый вакуум для каждой из фундаментальных сил. Всё, что мы знаем благодаря измерению тёмной энергии, — это то, каким должен быть их общий вклад. Когда мы пытаемся произвести такой расчёт, ответы, которые мы получаем, не имеют смысла и не дают нам значимой информации.

Но есть информация, которую трудно объяснить идеей о том, что сами флуктуации базисного пространства ответственны за квантовую неопределённость и распространение наблюдаемых нами волновых пакетов. Например, рассмотрим, что происходит, если взять квантовую частицу с присущим ей (спиновым) угловым моментом и заставить её двигаться в пространстве, прикладывая к ней магнитное поле.

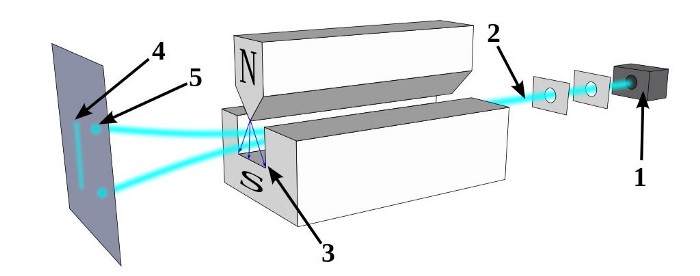
В показанном здесь опыте Штерна — Герлаха квантовая частица с конечным спином пропускается через магнитное поле, в результате чего спин становится чётко определённым в этом направлении: либо положительным (спин направлен вверх), либо отрицательным (спин направлен вниз). Каждая частица проходит тот или иной путь и после этого больше не имеет неопределённости в своём спине вдоль оси приложенного магнитного поля. Мы получаем набор дискретных значений (5), а не континуум значений (4), как можно было бы ожидать, если бы спины были случайно ориентированы в трёхмерном пространстве. (Автор (ы): Tatoute/Wikimedia Commons)

Эта частица отклонится на положительную или отрицательную величину: это зависит от направления приложенного к ней магнитного поля и от того, в каком направлении будет ориентирован спин частицы — положительном или отрицательном. Отклонение происходит вдоль координаты, в которой действует магнитное поле.

Теперь приложите магнитное поле в другом, перпендикулярном направлении. Вы уже определили, каким был спин в одном направлении. Так что же произойдёт, если приложить магнитное поле в другом направлении?

Ответ состоит в том, что частица отклонится снова в направлении поля или против него с вероятностью 50/50.

Но это ещё не самое интересное. Самое интересное заключается в том, что сам акт измерения, применение дополнительного, перпендикулярного поля, фактически уничтожает информацию, полученную ранее при применении первого магнитного поля. Если затем применить идентичное поле, которое мы применили в первой части эксперимента, эти частицы, даже если все они были ранее положительно ориентированы, снова будут иметь случайные спины: 50/50, ориентированные в направлении поля или против него.

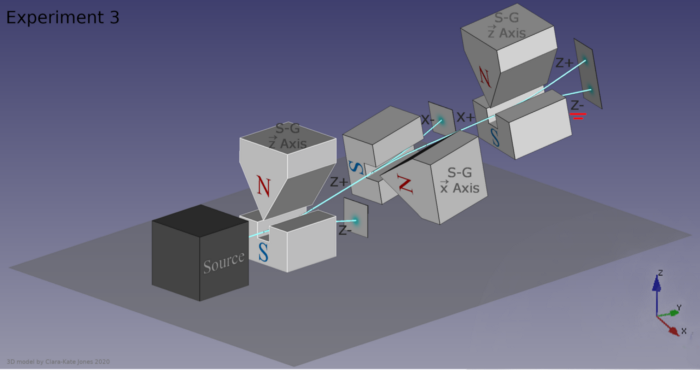
При пропускании потока частиц с квантовым спином через магнит направленного действия он разделится как минимум в 2 направлениях, в зависимости от ориентации спина. Если установить другой магнит с тем же направлением поля, дальнейшего разделения не последует. Однако, если между двумя магнитами установить третий, сориентированный перпендикулярно этим двум, это приведёт не только к разделению частиц в новом направлении, но и к уничтожению информации, полученной о начальном направлении, в результате чего частицы снова расщепятся при прохождении через последний магнит. (Автор (ы): MJasK/Wikimedia Commons)

Очень трудно найти этому объяснение, если предположить, что за всю квантовую неопределённость отвечает квантовый вакуум. В данном случае поведение частицы зависит от приложенного к ней внешнего поля и последующих взаимодействий, которые она испытала. Но не от свойств пустого пространства, через которое она прошла. Если убрать из упомянутой установки магнит, который ориентирован перпендикулярно двум другим, не будет никакой неопределённости спина частицы, пока она движется от магнита к магниту.

Трудно понять, как само «пустое пространство», или, если хотите, «квантовый вакуум» может быть ответственным за квантовую неопределённость, исходя из результатов этого эксперимента. Именно взаимодействия, которые испытывает квантовая система, или их отсутствие, а не какое-либо свойство, присущее полям, пронизывающим всё пространство, диктуют, как проявит себя квантовая неопределённость.

Нравится вам это или нет, но наблюдаемая реальность зависит от того, как и насколько внимательно вы наблюдаете. В зависимости от особенностей измерительной аппаратуры вы просто получаете разные результаты.

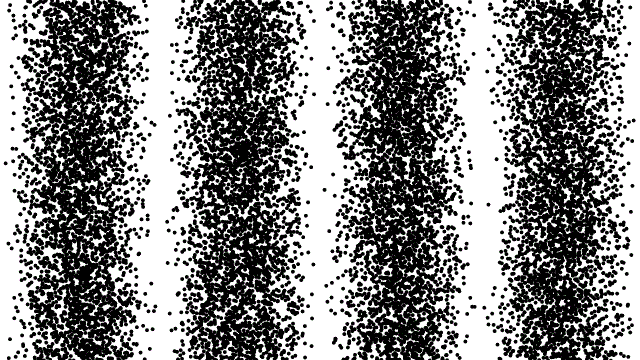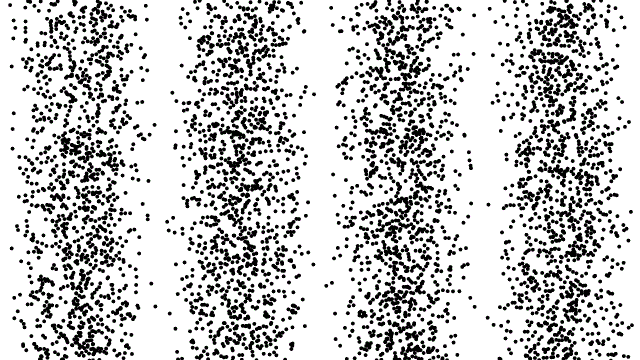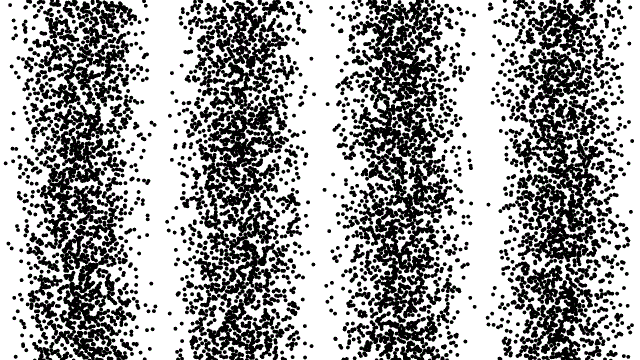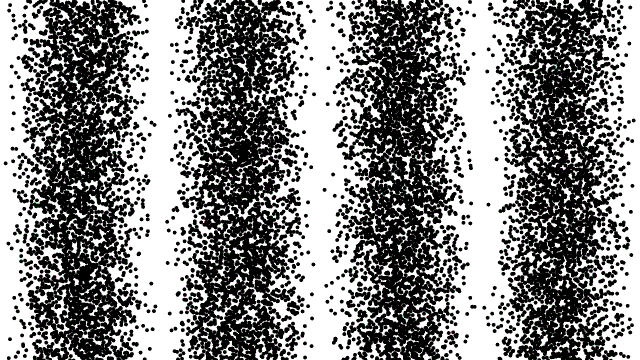
Возможно, двухщелевой опыт — самый пугающий из всех проведённых людьми квантовых опытов. Прошедшая через двойную щель частица окажется в области, вероятности которой определяются интерференционной картиной. При построении диаграммы на основании большого количества данных таких наблюдений вы сможете увидеть интерференционную картину, если эксперимент проведён правильно. Если вместо этого вы определяли, «через какую щель прошла каждая частица», вы получите не интерференционную картину, а две беспорядочных кучи частиц. (Автор (ы): Thierry Dugnolle/Wikimedia Commons)

По сей день ни одна теория скрытых параметров не привела к появлению экспериментальных данных или данных наблюдений, свидетельствующих о том, что существует глубинная объективная реальность, не зависящая от наших измерений. Многие люди подозревают, что это так, но это основано на интуиции и философских рассуждениях. Ни то, ни другое нельзя считать научно обоснованным основанием для любого умозаключения.

Это не значит, что нам пора прекратить строить такие теории и ставить опыты, чтобы выявить и исключить скрытые параметры. Ведь именно это и движет науку вперёд. Но до сих пор все подобные формулировки приводили лишь к ограничениям и опровержениям конкретных классов теорий скрытых параметров. Представление о том, что «есть скрытые параметры и все они закодированы в квантовом вакууме», тоже нельзя исключать.

Но, если бы я делал ставку на то, где искать их дальше, я бы отметил, что в (ньютоновской) теории гравитации также присутствуют сопряжённые переменные: гравитационный потенциал и плотность массы. Если аналогия с электромагнетизмом (между электрическим потенциалом и свободным электрическим зарядом) подтвердится, чего мы и ожидаем, это означает, что мы можем вывести соотношение неопределённостей и для гравитации.

Так что же, гравитация — это, по сути, квантовая сила, или нет? Однажды мы сможем определить экспериментально, есть ли в гравитации квантовая неопределённость. И если она есть, это и будет ответ.

А мы научим вас решать проблемы бизнеса научными методами, чтобы вы прокачали карьеру или стали востребованным IT-специалистом: Чтобы посмотреть все курсы, кликните по баннеру:

© Habrahabr.ru