[Перевод] Дизерпанк — статья о дизеринге изображений, которую мне хотелось бы прочитать01.08.2022 13:31

Мне всегда нравилась визуальная эстетика дизеринга (dithering, псевдотонирование, псевдосмешение цветов), но я не знал о том, как он применяется. Поэтому я провёл кое-какие изыскания. Эта статья может содержать отголоски ностальгии, но в ней не будет никаких следов Лены.

Как я сюда попал?

Я, конечно, припозднился, но, наконец, поиграл в «Return of the Obra Dinn», самую свежую игру Лукаса Поупа, создателя знаменитой «Papers Please». «Obra Dinn» — это история-головоломка, которую я могу только порекомендовать. Но я программист, и моё любопытство этот проект разжёг тем, что это — 3D-игра (созданная с использованием движка Unity), которая рендерится с использованием всего лишь двух цветов и с применением дизеринга. Видимо, это называется «дизерпанк», и мне это нравится.

Скриншот из «Return of the Obra Dinn» Скриншот из «Return of the Obra Dinn»

Дизеринг, как я изначально его понимал, это техника, основанная на применении лишь небольшого количества цветов из некоей палитры. Цвета так хитро комбинируются, что мозгу зрителя кажется, что он видит множество цветов. Например, глядя на предыдущий рисунок, вам, возможно, покажется, что на нём представлено несколько уровней светлоты. А на самом деле их всего два — полностью белый цвет и полностью чёрный.

Тот факт, что я никогда не видел 3D-игру с дизерингом, подобным этому, возможно, объясняется тем, что цветовые палитры — это, в основном, достояние прошлого. Вы, может быть, помните работу в Windows 95 в 16-цветном режиме и игры вроде «Monkey Island».

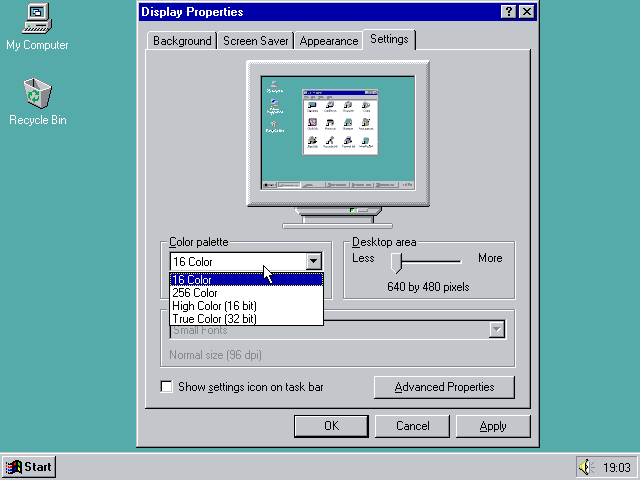Windows 95, настроенная на использование 16 цветов. А теперь потратим несколько часов на поиск правильного гибкого диска с драйверами, чтобы увидеть режим «256 цветов», или, ох, «True Color» Windows 95, настроенная на использование 16 цветов. А теперь потратим несколько часов на поиск правильного гибкого диска с драйверами, чтобы увидеть режим »256 цветов», или, ох, «True Color»Скриншот «The Secret of Monkey Island», где используется 16 цветов

Уже давно у нас имеется 8 бит на цветовой канал пикселя, что позволяет каждому пикселю на экране выводить один из 16 миллионов цветов. А учитывая то, что на горизонте виднеются технологии HDR и WCG, компьютерная графика уходит ещё дальше от ситуаций, в которых может хотя бы понадобиться какая-нибудь форма дизеринга. Но в «Obra Dinn», несмотря ни на что, дизеринг, всё же, используется. Эта игра вновь зажгла во мне давно забытую любовь. Я, после работы в Squoosh, кое-что знал о дизеринге. Поэтому был особенно впечатлён тем, как в этой игре дизеринг остаётся стабильным при перемещении и вращении камеры в трёхмерном пространстве. Мне хотелось разобраться с тем, как всё это работает.

Как оказалось, Лукас Поуп написал пост на форуме, в котором рассказал о том, какие техники дизеринга используются в игре, и о том, как они применяются в трёхмерном пространстве. Он проделал большую работу, чтобы сделать дизеринг стабильным при перемещениях камеры. После прочтения того поста я провалился в кроличью нору, а в этом материале я постараюсь рассказать о том, что там нашёл.

Дизеринг

Что такое дизеринг?

Из Википедии можно узнать о том, что дизеринг — это намеренное внесение в сигнал некоей разновидности шума, используемое для рандомизации ошибки квантования. Эта техника применима не только к изображениям. Она, до наших дней, используется и в звукозаписи. Но это — ещё одна кроличья нора, в которую можно будет провалиться как-нибудь в другой раз. Начнём с квантования.

Квантование

Квантование — это процесс отображения большого набора значений на меньший, обычно конечный, набор значений. В дальнейшем я, приводя примеры, буду использовать два следующих изображения.

Изображение-пример №1 («тёмное» изображение): чёрно-белая фотография моста «Золотые ворота» в Сан-Франциско, уменьшенная до 400×267 пикселейИзображение-пример №2 («светлое» изображение): чёрно-белая фотография моста между Сан-Франциско и Оклендом, уменьшенная до 253×400 пикселей

Обе чёрно-белые фотографии представлены в 256 оттенках серого. Если нужно будет использовать меньше цветов — например — только чёрный и белый, чтобы сделать изображения монохромными, придётся поменять цвет каждого пикселя, сделать каждый из них или полностью чёрным, или полностью белым. При таком сценарии чёрный и белый цвета называются «цветовой палитрой», а процесс изменения характеристик пикселей, которые не используют цвета из нашей палитры, называется «квантованием». Так как не все цвета из исходных изображений имеются в нашей цветовой палитре, это неизбежно приведёт к появлению ошибки, называемой «ошибкой квантования». Примитивное решение этой задачи заключается в том, чтобы квантовать каждый пиксель, приведя его цвет к цвету из палитры, наиболее близкому к исходному цвету пикселя.

Обратите внимание: определение того, какие цвета «близки друг к другу» — это вопрос, открытый для интерпретации. Ответ на него зависит от того, как измеряют расстояние между двумя цветами. Я исхожу из предположения о том, что мы, в идеале, измеряем расстояние между цветами с использованием психовизуальной модели. Но в большинстве найденных мной публикаций просто используется евклидово расстояние в RGB-кубе, вычисляемое по формуле $\sqrt{∆red^2+∆green^2+∆blue^2}$ .

Учитывая то, что наша палитра состоит лишь из чёрного и белого цветов, мы можем использовать светлоту пикселя для того чтобы решить, в какой цвет его квантовать. Светлота 0 — это чёрный цвет, светлота 1 — белый, а всё, что между ними, должно идеально коррелировать с человеческим восприятием. Таким образом, светлота 0.5 даст приятный средне-серый цвет. Для квантования заданного цвета нам лишь нужно сравнить его светлоту с 0.5, и, если светлота больше 0.5 — взять белый цвет, а если меньше — взять чёрный. Такое квантование вышеприведённых изображений приводит к… неудовлетворительным результатам.

grayscaleImage.mapSelf(brightness => 
  brightness > 0.5 
    ? 1.0 
    : 0.0
);

Обратите внимание: здесь приведены примеры рабочего кода, созданного на базе вспомогательного класса GrayImageF32N0F8, который я написал для демонстрационного материала к этой статье. Он похож на интерфейс ImageData, но использует Float32Array, имеет лишь один цветовой канал, представляющий значения между 0.0 и 1.0, и содержит множество вспомогательных функций. Исходный код можно найти здесь.

Цвет каждого пикселя был приведён, в зависимости от его светлоты, либо к чёрному, либо к белому цвету

Гамма-коррекция

Я завершил написание этой статьи и решил, так сказать, одним глазком глянуть на то, как будут выглядеть градиенты от чёрного к белому с использованием различных алгоритмов дизеринга. Результаты показали, что я не учёл того самого, что всегда становится проблемой при работе с изображениями. Речь идёт о цветовых пространствах. Я написал предложение «идеально коррелирует с человеческим восприятием», а сам не следовал этой идее.

Мои демонстрационные материалы созданы с использованием веб-технологий, и, самое главное, с помощью и ImageData, а они, в момент написания статьи, предусматривали использование цветового пространства sRGB. Это — старая спецификация (от 1996 года), в которой сопоставление значений и цветов смоделировано для отражения поведения CRT-мониторов. Хотя в наши дни почти никто не пользуется такими мониторами, sRGB всё ещё считается «безопасным» цветовым пространством, которое правильно выводится любым дисплеем. В результате — это цветовое пространство, по умолчанию, применяемое на веб-платформе. Но цветовое пространство sRGB нелинейно, то есть — (0.5,0.5,0.5) в sRGB — это не тот цвет, который человек видит, когда смешивают 50% (0,0,0) и (1, 1, 1). Это — тот цвет, который получают, подав половину мощности, необходимой для вывода полностью белого цвета, на электронно-лучевую трубку.

Градиент и результат его дизеринга в цветовом пространстве sRGB Градиент и результат его дизеринга в цветовом пространстве sRGB

Обратите внимание: я, при выводе большинства изображений в этой статье, применил свойство image-rendering: pixelated;. Это позволяет увеличивать страницу и реально видеть пиксели изображений. Но на устройствах с дробным значением devicePixelRatio это может привести к появлению артефактов. Если вы не уверены в том, что именно выводится на вашем экране — откройте изображение отдельно, в новой вкладке браузера.

На этом изображении видно, что градиент после дизеринга светлеет слишком быстро. Если нужно, чтобы 0.5 был бы цветом, находящимся между чёрным и белым цветами (как это воспринимается людьми), нужно преобразовать изображение из цветового пространства sRGB в RGB. Сделать это можно, прибегнув к процессу, называемому «гамма-коррекцией». В Википедии можно найти следующие формулы, предназначенные для преобразования между цветовым пространством sRGB и линейным RGB.

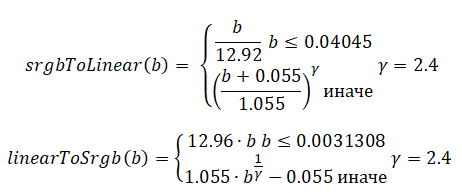Формулы для преобразования между цветовым пространством sRGB и линейным RGB. Прелестные формулы. И такие понятные Формулы для преобразования между цветовым пространством sRGB и линейным RGB. Прелестные формулы. И такие понятные

Применив эти преобразования, мы получаем (более) точный дизеринг градиента.

Градиент и результат его дизеринга в линейном цветовом пространстве RGB Градиент и результат его дизеринга в линейном цветовом пространстве RGB

Дизеринг со случайным шумом (random noise)

Вспомним, что говорится о дизеринге в Википедии. Дизеринг — это намеренное внесение в сигнал некоей разновидности шума, используемое для рандомизации ошибки квантования. С квантованием мы разобрались, а теперь поговорим о шуме. О намеренном внесении шума в сигнал.

Вместо того чтобы квантовать каждый пиксель напрямую, мы добавляем к пикселям шум, значения которого находятся между -0.5 и 0.5. Идея тут в том, что некоторые пиксели теперь будут квантоваться к «неправильным» цветам, но то, как часто это происходит, зависит от изначальной светлоты пикселя. Чёрные пиксели всегда остаются чёрными, белые всегда остаются белыми, а средне-серые будут, примерно в 50% случаев, оказываться чёрными. Со статистической точки зрения общая ошибка квантования снижается, а наш мозг охотно сделает всё остальное и поможет нам увидеть, так сказать, общую картину.

grayscaleImage.mapSelf(brightness =>
  brightness + (Math.random() - 0.5) > 0.5 
    ? 1.0 
    : 0.0
);

К каждому пикселю перед квантованием добавлен случайный шум [-0.5; 0.5] К каждому пикселю перед квантованием добавлен случайный шум [-0.5; 0.5]

Этот результат показался мне довольно-таки неожиданным! Не назову его «хорошим», видеоигры из 90-х показали нам, что такие картинки могут выглядеть куда лучше. Но перед нами — быстрый способ, не требующий особых усилий, позволяющий получить больше деталей на монохромном изображении. И если бы я понимал слово «дизеринг» буквально, то на этом я и окончил бы статью. Но это — далеко не всё.

Дизеринг с упорядоченным шумом (ordered dithering)

Вместо того чтобы говорить о том, какой именно шум добавить к изображению перед квантованием, можно изменить точку зрения и обсудить настройку порога квантования.

// Добавление шума
grayscaleImage.mapSelf(brightness =>
  brightness + Math.random() - 0.5 > 0.5 
    ? 1.0 
    : 0.0
);

// Настройка порога квантования
grayscaleImage.mapSelf(brightness => 
  brightness > Math.random() 
    ? 1.0 
    : 0.0
);

В контексте монохромного дизеринга, где порог квантования равен 0.5, эти два подхода эквивалентны:

brightness+rand()-0.5 > 0.5
↔          brightness > 1.0-rand()
↔          brightness > rand()

Положительный момент этого подхода в том, что мы можем говорить о «матрице пороговых значений». Матрицы пороговых значений можно визуализировать. Это облегчит обсуждение того, почему результирующее изображение выглядит так, как выглядит. Ещё их можно вычислять заранее и использовать многократно, что делает процесс дизеринга детерминистическим и поддающимся параллелизации на уровне каждого пикселя. В результате дизеринг можно выполнять на GPU в виде шейдера. Именно так сделано в «Return of the Obra Dinn»! Есть несколько различных подходов к генерированию матриц пороговых значений, но все они каким-то образом упорядочивают шум, который добавляют к изображению. Отсюда и название этого метода — «дизеринг с упорядоченным шумом», или «дизеринг с упорядоченным возбуждением».

Матрица пороговых значений для вышеприведённого примера дизеринга — это, в буквальном смысле, матрица, полная случайных пороговых значений, называемых ещё «белым шумом» (white noise). Это название пришло из сферы обработки сигналов, где каждая частота имеет одинаковую интенсивность, как, например, в белом свете.

Матрица пороговых значений — это, по определению, белый шум Матрица пороговых значений — это, по определению, белый шум

Дизеринг Байера (Bayer dithering)

Дизеринг Байера использует в роли матрицы пороговых значений матрицу Байера. Эти сущности названы в честь Брюса Байера, создателя фильтра Байера, который до наших дней используется в цифровых фотоаппаратах. Каждый пиксель светочувствительной матрицы может регистрировать лишь яркость света. Но если перед отдельными пикселями по-умному разместить цветные фильтры, можно восстановить цветное изображение посредством алгоритма демозаизации. Шаблон для этих фильтров — это тот же шаблон, что используется в дизеринге Байера.

Матрицы Байера бывают разных размеров, которые я, в итоге, стал называть «уровнями». Матрица Байера уровня 0 — это матрица 2×2. Уровень 1 — это матрица 4×4. А матрица уровня — это матрица $2^{n+1}×2^{n+1}$ . Матрицу уровня n можно рекурсивно вычислить из матрицы уровня n-1 (хотя в Википедии, кроме того, упомянут алгоритм, основанный на работе с отдельными ячейками). Если ваше изображение оказалось больше, чем матрица Байера, можно обработать его, расположив несколько матриц пороговых значений рядом друг с другом.

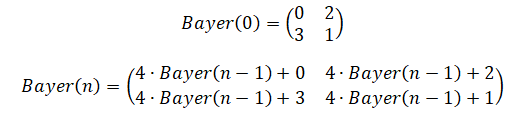Рекурсивное определение матриц Байера

Матрица Байера уровня n содержит числа от 0 до $2^{2n+2}$ После того, как вы нормализуете матрицу Байера, то есть — разделите на $2^{2n+2}$ , её можно использовать как матрицу пороговых значений:

const bayer = generateBayerLevel(level);
grayscaleImage.mapSelf((brightness, { x, y }) =>
  brightness > bayer.valueAt(x, y, { wrap: true }) 
    ? 1.0 
    : 0.0
);

Хочу отметить тут одну деталь: дизеринг Байера использующий матрицы, такие, которые определены выше, даст итоговое изображение, которые будет светлее исходного. Например — в области, где каждый пиксель имеет светлоту 1/255=0.4%, матрица Байера размера 2×2 сделает белым каждый из четырёх пикселей, что даст итоговую среднюю светлоту в 25%. Эта ошибка становится меньше при применении матриц Байера более высоких уровней, но фундаментальное отклонение от оригинала при этом остаётся таким же.

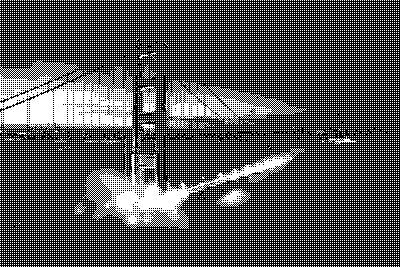Почти чёрные участки изображения становятся заметно светлее

На нашем «тёмном» тестовом изображении небо не полностью чёрное, оно, при применении матрицы Байера уровня 0, оказывается значительно светлее. Хотя ситуация улучшается на более высоких уровнях, альтернативным решением может стать инвертирование отклонения, что приводит к получению изображений, которые темнее оригинала. Это делается путём обращения механизма использования матрицы Байера:

const bayer = generateBayerLevel(level);
grayscaleImage.mapSelf((brightness, { x, y }) =>
  //Обратите внимание на "1 -” в следующей строке
  brightness > 1 - bayer.valueAt(x, y, { wrap: true }) 
    ? 1.0 
    : 0.0
);

Я использовал исходное определение матрицы Байера для «светлого» изображения и инвертированную версию для «тёмного» изображения. Лично мне больше всего нравятся результаты, полученные на уровнях 1 и 3.

Дизеринг Байера уровня 0Дизеринг Байера уровня 1Дизеринг Байера уровня 2Дизеринг Байера уровня 3

Дизеринг с синим шумом (blue noise)

И у подхода к дизерингу, когда применяется белый шум, и у того, где используется матрица Байера, конечно, есть недостатки. Для дизеринга Байера, например, характерно наложение на изображение повторяющихся структур, которые, особенно, если увеличить изображение, оказываются заметными. Белый шум — это набор случайных значений, что неизбежно ведёт к появлению на матрице пороговых значений «кластеров» из светлых пикселей и «пустот» из тёмных пикселей. Эти факты можно сделать более очевидными, если наклонить, или, если это для вас слишком сложно, алгоритмически размыть матрицу пороговых значений. «Кластеры» и «пустоты» могут плохо подействовать на результаты дизеринга. Если тёмные области изображения придутся на один из «кластеров» — в соответствующей области выходного изображения будут потеряны детали (и, наоборот, для светлых областей изображения, пришедшихся на «пустоты»).

Чёткие «кластеры» и «пустоты» остаются видными даже при размытии изображения по Гауссу (σ = 1.5) Чёткие «кластеры» и «пустоты» остаются видными даже при размытии изображения по Гауссу (σ = 1.5)

Существует разновидность шума, называемая «синим шумом», нацеленная на решение этой проблемы. Этот шум называют «синим» из-за того, что сигналы более высоких частот в нём имеют более высокие интенсивности, чем сигналы более низких частот (как в случае с синим светом). Убирая или заглушая низкие частоты, можно сделать так, что «кластеры» и «пустоты» оказываются менее выраженными. Дизеринг с синим шумом выполняется так же быстро, как и дизеринг с белым шумом — в итоге это просто матрица пороговых значений, но генерирование синего шума немного сложнее и ресурсозатратнее.

Наиболее распространённый алгоритм генерирования синего шума, похоже, это «метод пустот и кластеров» («void-and-cluster method») Роберта Улични. Вот публикация, где это описано. По-моему, описание алгоритма не отличается интуитивной понятностью, а теперь, когда я его реализовал, я убедился в том, что он описан в чрезмерно абстрактном стиле. Но алгоритм это весьма толковый!

Алгоритм основан на идее, в соответствии с которой можно найти пиксель, являющийся частью «кластера» или «пустоты», обработав изображение с помощью эффекта размытия по Гауссу и найдя самый светлый (или, соответственно, самый тёмный) пиксель на размытом изображении. После инициализации чёрного изображения с помощью нескольких случайно расположенных белых пикселей, алгоритм приступает к непрерывной замене пикселей «кластеров» и «пустот», стремясь как можно равномернее распределить по изображению белые пиксели. После этого каждому пикселю назначается номер между 0 и (где — общее количество пикселей) в соответствии с их важностью для формирования «кластеров» и «пустот». Подробности об этом смотрите здесь.

Моя реализация этого алгоритма работает хорошо, но не очень быстро, так как я не тратил много времени на её оптимизацию. На моём MacBook 2018 года генерирование текстуры синего шума размером 64×64 занимает около минуты. Для наших целей этого достаточно. Если нужно что-то побыстрее — стоит обратить внимание на оптимизацию, касающуюся эффекта размытия по Гауссу, но не в пространственной области, а в частотной области.

Отступление: конечно, я, когда это узнал, увидел интересную задачу, которую просто не мог не решить. Перспективность этой оптимизации объясняется свёрткой (это — внутренний механизм размытия по Гауссу), которой приходится проходиться по каждому полю ядра размытия по Гауссу для каждого пикселя изображения. Но если перевести и изображение, и ядро размытия по Гауссу в частотную область (используя один из многих алгоритмов быстрого преобразования Фурье), свёртка превращается в поэлементное умножение. Так как размер целевой текстуры синего шума — это степень двойки — я мог реализовать хорошо исследованный in-place-вариант алгоритма быстрого преобразования Фурье Кули — Тьюки. После нескольких первоначальных неудач я смог уменьшить время генерирования текстуры синего шума на 50%. Код у меня получился довольно-таки посредственный, поэтому тут найдётся место и для дальнейших оптимизаций.

Текстура синего шума размером 64×64, обработанная с помощью размытия по Гауссу (σ = 1.5). Чётких структур на размытом варианте изображения не осталось

Синий шум основан на размытии по Гауссу, которое вычисляется на тороидальной структуре (это — замысловатый способ сказать, что алгоритм на краях изображения «сворачивается»). В результате изображение можно бесшовно «замостить» текстурами синего шума. Поэтому можно воспользоваться текстурой размера 64×64 и покрыть её копиями всё изображение. Дизеринг с синим шумом даёт приятную, сбалансированную отрисовку деталей, не выдавая заметных повторяющихся паттернов. Итоговое изображение смотрится органично.

Дизеринг с синим шумом Дизеринг с синим шумом

Дизеринг с рассеянием ошибки (error diffusion)

Все вышеописанные подходы к дизерингу основаны на том факте, что ошибки квантования статистически сглаживаются из-за того, что пороговые значения в соответствующей матрице распределены равномерно. Но есть и другой подход к квантованию, связанный с рассеянием ошибки. Вы, скорее всего, встречались с ним, если когда-нибудь интересовались дизерингом. Применяя этот подход, мы не просто выполняем квантование изображения, надеясь, что, в среднем, ошибка квантования останется незначительной. Вместо этого мы измеряем ошибку квантования и рассеиваем эту ошибку на соседние пиксели, влияя на то, как они будут квантоваться. Мы, по сути, в процессе работы меняем изображение, которое хотим подвергнуть дизерингу. Это делает процесс преобразования изображения, по сути, последовательным.

Предостережение: одним из больших плюсов алгоритмов рассеяния ошибки, о котором мы не говорим в этом материале, является тот факт, что эти алгоритмы способны работать с произвольными цветовыми палитрами. А дизеринг с упорядоченным шумом требует, чтобы цвета на цветовой палитре были бы расположены с равными интервалами. Подробнее об этом я расскажу как-нибудь в другой раз.

Почти все подходы к дизерингу с рассеиванием ошибки, которые я собираюсь рассмотреть, используют «матрицу рассеяния», которая определяет то, как ошибка квантования текущего пикселя распространяется по соседним пикселям. При работе с такими матрицами часто считается, что пиксели изображения просматриваются сверху вниз и слева направо — так же, как читают тексты жители Запада. Это важно, так как ошибка может быть рассеяна лишь на пиксели, которые ещё не подверглись квантованию. Если вы будете обходить изображения в порядке, не соответствующем тому, на который рассчитана матрица рассеяния, соответствующим образом отразите матрицу.

Дизеринг с «простым» двумерным рассеянием ошибки

Примитивный подход к дизерингу с рассеянием ошибки предусматривает распространение ошибки квантования на пиксель, который находится ниже текущего, и на пиксель, находящийся справа от него. Это можно описать следующей матрицей:

Матрица рассеяния ошибки, переносящая половину ошибки на 2 соседних пикселя. Знаком »*» отмечен текущий пиксель

Алгоритм рассеяния ошибки посещает каждый пиксель изображения (в правильном порядке), квантует текущий пиксель и измеряет ошибку квантования. Обратите внимание на то, что значение ошибки квантования имеет знак, то есть — оно может быть отрицательным, если квантование делает пиксель светлее, чем исходный пиксель. Затем части ошибки добавляют к соседним пикселям в соответствии с матрицей. Потом этот процесс повторяется для следующего пикселя.

Пошаговая визуализация алгоритма рассеяния ошибки

Эта анимация предназначена для визуализации алгоритма, но она не способна показать то, как результаты дизеринга соотносятся с оригиналом изображения. Области размером 4×4 пикселя вряд ли достаточно для того, чтобы рассеять и усреднить ошибки квантования. Но тут можно видеть то, что если пиксель в ходе квантования делается светлее, то соседние пиксели, чтобы это скомпенсировать, делаются темнее (и наоборот).

Простой дизеринг с двумерным рассеянием ошибки Простой дизеринг с двумерным рассеянием ошибки

Но простота матрицы рассеяния делает рассматриваемый подход к дизерингу подверженным появлению различимых паттернов, вроде паттернов в виде линий, которые можно видеть на вышеприведённых изображениях.

Дизеринг по алгоритму Флойда — Стейнберга (Floyd-Steinberg)

Алгоритм Флойда — Стейнберга — это, пожалуй, один из самых известных алгоритмов рассеяния ошибки, а, возможно, это — самый известный алгоритм, применяемый при дизеринге изображений. Он использует более сложную матрицу рассеяния ошибок, которая позволяет распределять ошибку на все непосещённые пиксели, являющиеся непосредственными соседями текущего пикселя. Числа в этой матрице тщательно подобраны для того чтобы как можно сильнее уменьшить возможность образования повторяющихся паттернов.

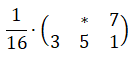Матрица рассеяния ошибки Роберта У. Флойда и Луиса Стейнберга

Применение алгоритма Флойда — Стейнберга — это большой шаг вперёд в нашем исследовании, так как это позволяет предотвращать возникновение множества паттернов. Но и при его применении большие пространства изображения с незначительным количеством деталей всё ещё могут выглядеть не очень хорошо.

Дизеринг с применением алгоритма рассеяния ошибки Флойда — Стейнберга Дизеринг с применением алгоритма рассеяния ошибки Флойда — Стейнберга

Дизеринг по алгоритму Джарвиса — Джудиса — Нинке (Jarvis-Judice-Ninke)

В алгоритме Джарвиса — Джудиса — Нинке используется ещё большая матрица рассеяния ошибки. Ошибка распределяется на большее количество пикселей, а не только на те, которые находятся в непосредственной близости от текущего пикселя.

Матрица рассеяния ошибки Д. Ф. Джарвиса, С. Н. Джудиса и У. Х. Нинке из лабораторий Белла Матрица рассеяния ошибки Д.Ф. Джарвиса, С.Н. Джудиса и У.Х. Нинке из лабораторий Белла

Использование такой матрицы рассеяния ошибки ведёт к дальнейшему снижению вероятности образования паттернов. И хотя на тестовых изображениях имеются паттерны в виде линий, теперь они не так сильно бросаются в глаза.

Дизеринг по алгоритму Джарвиса — Джудиса — Нинке Дизеринг по алгоритму Джарвиса — Джудиса — Нинке

Дизеринг по алгоритму Аткинсона (Atkinson)

Алгоритм Аткинсона был разработан в компании Apple Биллом Аткинсоном и получил известность благодаря его использованию в ранних компьютерах Macintosh.

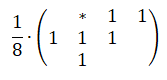Матрица рассеяния ошибки Билла Аткинсона

Стоит отметить, что матрица рассеяния ошибки Аткинсона состоит из шести единиц, но она нормализуется с использованием 1/8, то есть — она не переносит всю ошибку на соседние пиксели, увеличивая воспринимаемую контрастность изображения.

Дизеринг по алгоритму Аткинсона Дизеринг по алгоритму Аткинсона

Дизеринг по алгоритму Римерсма (Riemersma)

Честно говоря, на алгоритм Римерсма я наткнулся случайно. Я, пока исследовал другие алгоритмы, нашёл одну обстоятельную статью, в которой было написано об этом алгоритме. Такое ощущение, что он не особенно широко известен, но он мне очень понравился. Понравились мне и те идеи, на которых он основан. Вместо того, чтобы, ряд за рядом, обходить изображение, он обходит изображение по кривой Гильберта. С технической точки зрения тут подошла бы любая кривая, заполняющая пространство. Но рекомендуется использовать именно кривую Гильберта. Этот алгоритм довольно просто реализовать с использованием генераторов. Благодаря этому алгоритм нацелен на то, чтобы взять лучшее из алгоритмов дизеринга с упорядоченным шумом и с рассеянием ошибки. Речь идёт об ограничении количества пикселей, на которые может подействовать один пиксель, а так же о приятном внешнем виде результата (и о скромных требованиях к памяти).

Визуализации кривой Гильберта размером 256×256. Чем позже кривая посещает пиксели — тем светлее они становятся

У кривой Гильберта есть свойство «локальности», которое выражается в том, что пиксели, находящиеся близко друг к другу на кривой, находятся близко друг к другу и на изображении. При таком подходе нам не нужно использовать матрицу рассеяния ошибки. Вместо этого достаточно применить последовательность рассеяния ошибки длиной n. Для квантования текущего пикселя к нему добавляются n последних ошибок квантования с весами, заданными в последовательности рассеяния ошибки. В вышеупомянутой статье для задания весов используется экспоненциальный спад. Ошибке квантования предыдущего пикселя назначается вес 1, самой старой ошибке квантования в списке назначается маленький, вычисляемый по особой формуле, вес . Для вычисления -го веса используется следующая формула:

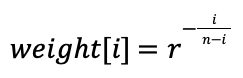
В статье рекомендуется использовать r=1/6 , а минимальный размер списка значений — n=16 , но, выполняя тесты, я обнаружил, что лучше всего выглядит изображение с r=1/8 и n=32

Дизеринг по алгоритму Римерсма с r=1/8 и n=32 Дизеринг по алгоритму Римерсма с r=1/8 и n=32

Результат выглядит чрезвычайно органично, почти так же приятно, как после дизеринга с синим шумом. И, в то же время, дизеринг по алгоритму Римерсма легче реализовать, чем оба предыдущих варианта. Это, правда, всё равно, алгоритм, основанный на рассеянии ошибки, то есть — он обрабатывает данные последовательно и не подходит для выполнения на GPU.