Жадный алгоритм, ветви и границы для расписания мерчендайзеров (кейс Хакатона на оптимизацию)11.05.2021 17:17

Это пилотная статья. Будем благодарны за обратную связь. Если тема вызовет интерес, мы возможно примем решение выложить на GitHub наши исходники (python) и входные data-set«ы.

В марте 2021 г. случилось мне поучаствовать в хакатоне с задачей на комбинаторику и оптимизацию. Команду решил собрать свежую, из одиночек, дрейфующих в пуле самого хака. Довольно быстро нашлись front и back, и втроем мы принялись старательно думать, как потратим деньги, когда выиграемJ Так как сам кейс показался нам по началу не сложным. Надо сказать, что в хаках я не так давно, но уже успел поучаствовать и в ЛЦТ (Лидеры Цифровой Трансформации), и в Цифровом Прорыве. В последнем даже удалось занять бронзу в финале. Роль всегда у меня была project+product+ppt (хотя опыт в программировании у меня также имеется). Не редко в хакатонских кейсах проблемы немного надуманы, решения этих проблем немного фееричны и не несут практического смысла, а побеждает профессиональная преза и поставленный питч. Так вот этот мартовский хакатон меня заинтересовал живостью и насущностью бизнес проблем, которые там решались. Опытные хакатонщики, читающие эти строки, поймут. Но полно про хакатоны и про то, какие они бывают, а то собьемся с курса.

В этам хаке преза и даже front мало интересовали кейсодержателей. Это был натуральный бизнес хакатон с абсолютно живыми дата сетами и с натуральной бизнес болью. Кстати на хакатоне ни одна из команд не предоставила решение. Вроде одни ребята «нарисовали» в своей презе оптимизацию в минус 1 агент, но демонстрацию на защите они не представили. Наша команда не стала исключением и заняла скромное третье место (всего до защиты дошло 5 команд). Теперь наконец к условию:

Есть 204 ТТ (торговые точки). Каждую из них нужно посетить минимум раз в неделю, а некоторые больше одного раза. Длительности посещения каждой ТТ известны и не изменяются внутри недели.

Также предоставлена матрица 204×204 с расстояниями между точками (см. Табл. 1 ниже). Матрица не симметричная, т.к. при составлении учитывались знаки ПДД (одностороннее движение и пр.). Видимо она была получена через API Яндекс.Карт по адресам ТТ. Требовалось найти оптимальное расписание для торговых агентов (мерчендайзеров), улучшив показатели текущего AS IS (оно тоже предоставлено). Важные ограничения: каждая ТТ должна быть закреплена за определенным мерчендайзером (торговым агентом). Другими словами, если торговый агент (далее агент) посещает Магнит на улице Ленина в понедельник, то этот же Магнит в другие дни недели должен посещать именно он. Время работы каждого агента не должно превышать 9,5 часов в день с учетом работы в ТТ и перемещению между ними.

Таблица 1. Матрица расстояний между точками

Предоставленное  расписании AS IS распределено на 14 агентов. И как вы уже догадались, решение должно было предложить альтернативное расписание, сократив по возможности количество агентов и их время в пути.

Спустя какое-то время после хакатона наш back (python) призвал на помощь коллегу с курсов по deep learning. Парни погуглили, поискали готовый алгоритм, почитали про метод отжига, муравьев, генетику и пришли еще раз к выводу, что подходящего метода и примеров кода именно для этой задачи, куда можно было бы взять и вставить матрицу расстояний, как входной параметр на просторах интернета — нет. Если кто знает где есть — поделитесь, будем благодарны.

Позднее, и даже в параллель я сам начал изучать тему Задачи коммивояжера и эвристические методы, зарекомендовавшие себя для ее решения. Но ни хабр, ни youtube, ни Википедия не давали готового ответа именно для этого частного случая. Останавливаться все равно не хотелось. Наоборот, по мере продвижения вперед интерес подогревался. Мотивации добавило то, что классическая задача коммивояжера относится к NP полным задачам. Если решать задачу полным перебором (brutal force), то уже при 66 торговых точках нужно несколько миллиардов лет и компьютер размером с Землю. Согласитесь, мощь трансвычислительных задач завораживает! И действительно, для решения классической задачи TSP (Travelling salesman problem) существуют различные эвристические методы, такие как Метод Имитации Отжига, Муравьиный алгоритм, Генетический метод и др. Оставалось решить один вопрос: как применить что-то из этой эвристики к сквозному недельному расписанию нескольких торговых агентов с ограничением по времени. Возможно толковый математик, который кожей чувствует физический смысл дифференцирования, логарифмов, пределов, силу числа e и т.д., справился бы с этой задачей. Но я не такой математик. Формулы счастья по-прежнему в интернете не находилось. Я даже изучил основы нейросетей, но когда я начинал проектировать свою нейросеть для решения — вырастала непреодолимая стена.

И все-таки решение родилось! Ну во-первых я обратился за помощью к своему коллеге, Черкасову Евгению @eny01. Он как раз недавно прошел курсы по data science и python, и рвался в бой, чтобы применить все приобретённые навыки. К слову сказать, бОльшую часть алгоритма именно он и разработал. Себе я взял часть, отвечающую за рекурсивный метод ветвей и границ. Но об этом позже. Вдвоем мы разработали следующий план.

1. Мы декомпозировали задачу до каждого агента. Набираем ТТ сначала для одного агента до предела по очереди для всех дней недели, затем для второго и т.д.;

2. Процесс набора ТТ происходит с помощью жадного алгоритма (метод ближайшего соседа);

3. В случае, когда набор подходит к пределу (9,5 часов) — применяем оптимизацию и считаем, что для данного агента в этот день недели оптимальное расписание составлено. Переходим к следующему дню;

 Алгоритм набора расписания для каждого агента более подробно можно увидеть на блок-схеме ниже:

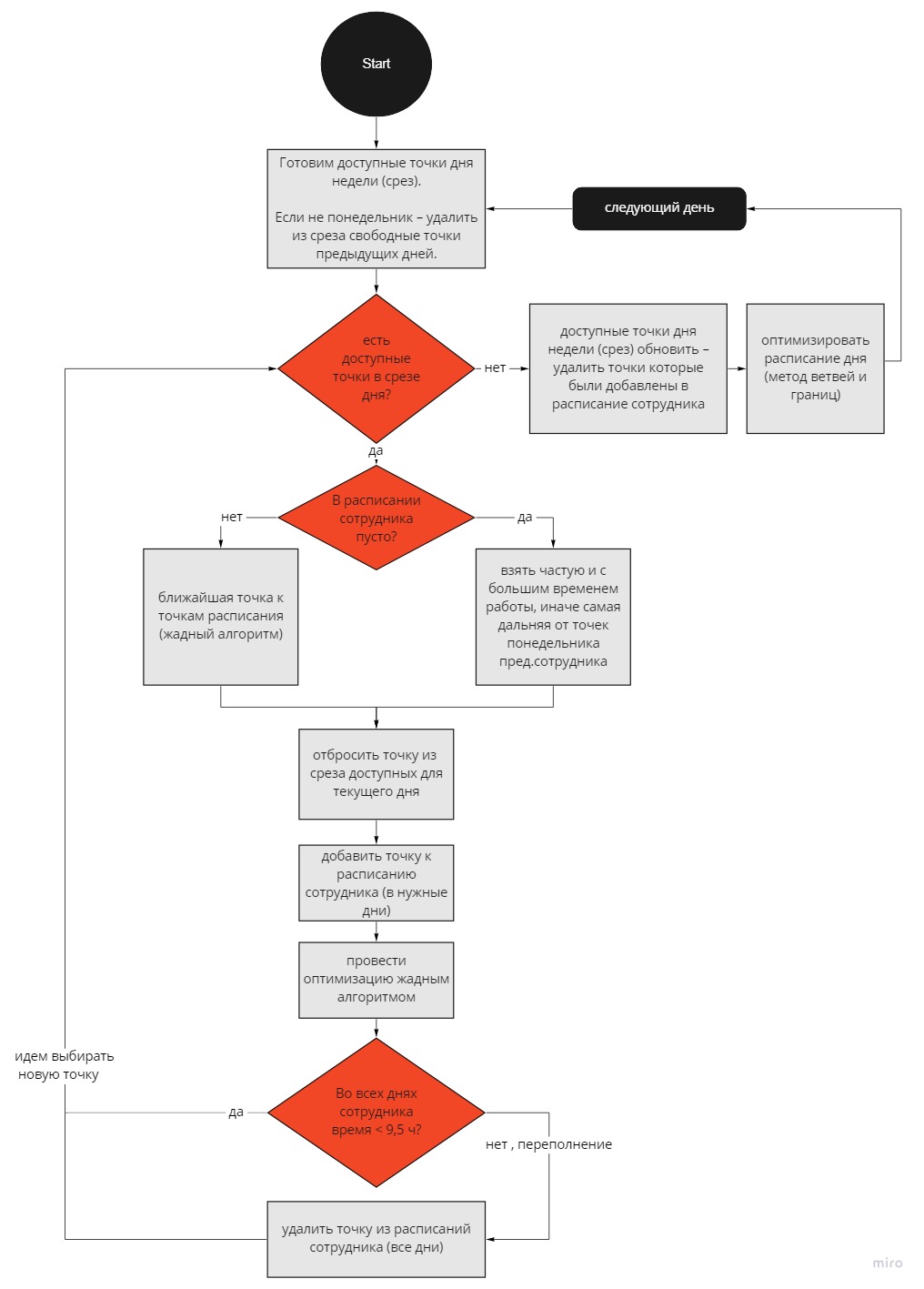
Теперь чуть подробнее про основные моменты:

1. Ближайшие сосед:

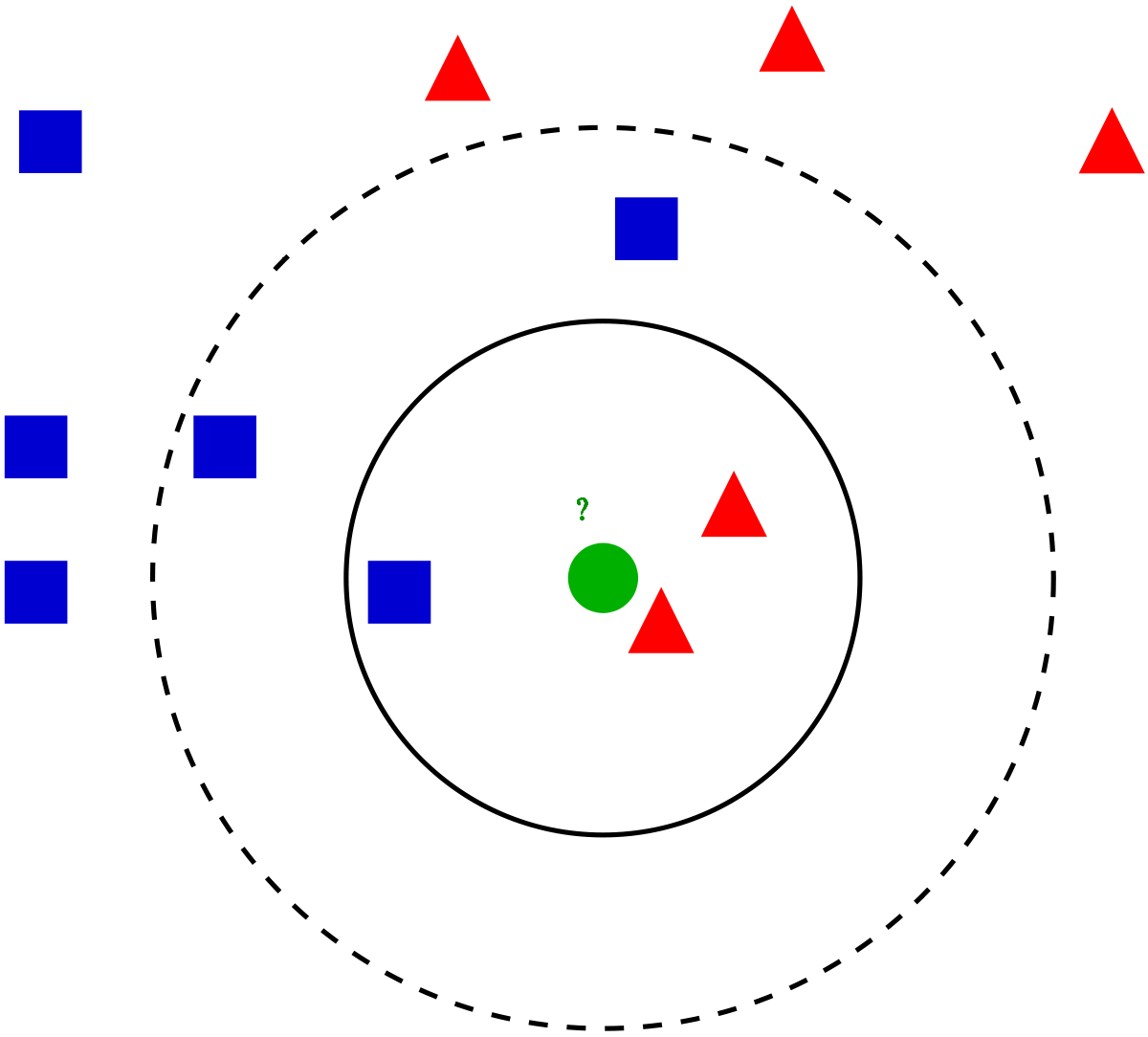
Первой точкой расписания дня недели мы берем точку, наиболее объемную по времени посещения и наиболее частую в неделе. Второй и последующими точками становятся ближайшие к уже отобранным точкам. Каждый раз при добавлении новой точки в расписание дня производится оптимизация по подбору наилучшей первой точки для получаемого кратчайшего пути в расписании. Мы попросту перебираем точки, подставляя каждую в качестве первой и перенабираем к ней при помощи того же жадного алгоритма отдельный массив. В итоге выбираем самый лучший вариант по минимальному пути для прохождения точек.

Важно следить за переполнением не только в том дне, в котором идет набор, но и параллельно приглядывать за остальными днями торгового представителя- последующими и предыдущими. Так как выбирая точку, скажем для четверга, мы можем переполнить ею пятницу или понедельник.

Когда в одном из дней достигается предел рабочего времени (>=9,5 ч.), система сбрасывает точку приведшую к переполнению и пробует добрать следующую ближайшую. Кстати, мы пробовали вставлять сюда вместо оптимизации «первой точки» и ближайшего соседа полный перебор с ветвями и границами. И результат, ! внимание!, получался в итоге тот же. Но времени на перебор с ветвями и границами потребовалось гораздо больше. Около 3,5 часов против 5 минут для всех 204 точек. Таким образом полный перебор был абсолютно избыточен и неэффективен при частом применении. Вследствие чего в этом месте было решено от перебора с ветвями и границами отказаться, но добавить его в финальную оптимизацию составленного расписания.

2. Метод ветвей и границ:

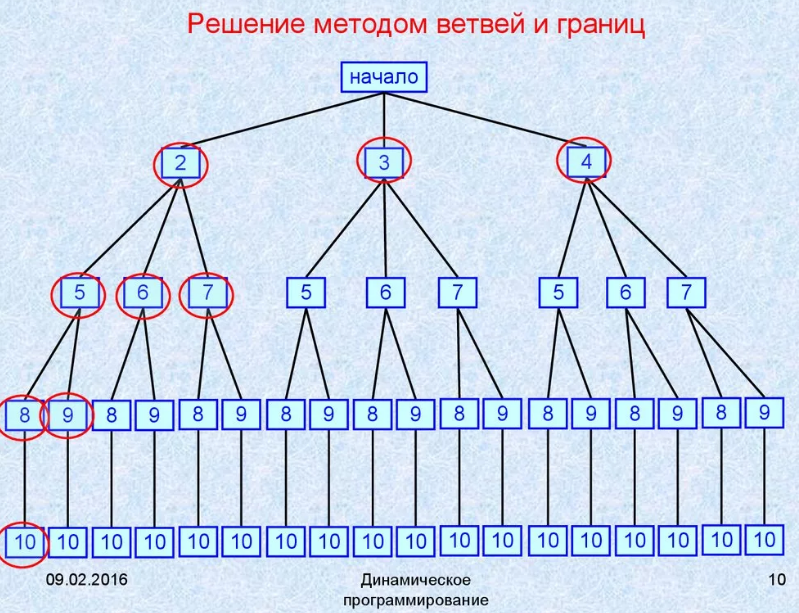
Ну тут все относительно просто. Утвержденное недельное расписание мы прогоняем через полный перебор, используя метод ветвей и границ. Реализация этой функции потребовала применения рекурсии. Причем если сравнивать работу полного перебора через библиотеку itertools (python), то время на перебор 8 точек составило 21 сек, в то время как наша рекурсия с ветвями и границами отрабатывала за 0.4 с. Что не может не радовать! Цель применения ветвей и границ — оптимизация уже готовых расписаний. Привязка ТТ и агентов уже не меняется, но оптимизируется время в пути (решаем классическую задачу коммивояжера).

Результаты:

Описанным выше образом мы производим набор точек для второго агента, затем для третьего и т.д. В результате работы алгоритма нам удалось не только снизить количество агентов с 14 до 13, но и сократить суммарную траекторию перемещения между ТТ вдвое. Ниже представлены результаты, которых нам удалось добиться:

Время работы алгоритма для всех агентов на всех днях недели составило 8 минут на домашнем ПК.

И в качестве финального аккорда мы позволили себе выкрутить лимит с 9 часов 30 минут до 9 часов 38 минут. И получили сокращение до 12 агентов с небольшой погрешностью. Из 60 дневных  расписаний 14 уходят в переработки от 1 до 8 минут (51 минута в сумме).

Ждем ваших комментариев, замечаний и предложений! Ответим на все вопросы. Пишите, как бы вы решали эту задачу. Особенно ценны для нас будут мнения практиков. Как математиков, так и data science’ов. Возможно кто-то предложит существующие библиотеки python для решения задачи. Мы, как я уже сказал, подходящих библиотек не нашли. Всем спасибо, что дочитали до конца!