Возможна ли жизнь без оптимальных решений и прогнозов04.05.2022 12:16

Передо мной книга «Модельное мышление» Скотта Пейджа (издательство «Манн, Иванов и Фербер», Москва, 2020). По словам автора, «В книге рассматривается подход под названием «многомодельное мышление» — использование совокупности моделей для осмысления сложных явлений».

Тема эта не нова. Достаточно привести примеры публикаций популярных англосаксонских авторов Дж. Д. Вильямса (1), Л. Мозеса (2), Д. Химмельблау (3). Есть публикации и отечественных авторов (4). Отметим, что эти вопросы на различных уровнях неоднократно освещались уже 60 и 40 лет назад.

Ниже для читателей блога ЛАНИТ кратко изложены содержащиеся в книге принципы многомодельного подхода и инструменты для создания моделей.

— Ты хорошо знаешь математическую статистику?
— Да нет, наверное…
(Разговор двух студентов)
Есть три вида лжи: Ложь, Наглая ложь и Статистика
(Марк Твен)

Зачем нужна многомодельность

Перед принятием какого-либо решения человек всегда прогнозирует ситуацию, даже в простейших случаях — при покупке продуктов, бытовой техники, не говоря уже о кардинальных решениях — выборе профессии, места обитания. При принятии решений при управлении производственными процессами, тем более социальными явлениями прогнозирование возможных ситуаций приобретает решающую роль. Пытливые умы давно задумывались над возможностью формализовать процесс принятия решения в условиях неопределенности. Еще в XVIII веке Бернулли предложил уравнение, названное его именем, которое оценивает вероятность выпадения той или иной стороны монеты при случайном бросании. Некоторые экспериментаторы не поленились и провели до 20 000 бросаний монеты, чтобы убедиться в справедливости уравнения.

Согласно определению Д. Химмельблау (3), модель есть математическое описание реального процесса. Традиционный подход к стандартной практике построения моделей основан на принципе — одна задача требует одной модели, нужно найти одну подходящую модель и правильно ее применить. Одна простая модель на основе вероятностной оценки события при использовании подхода — как часто может появиться белое или черное, орел или решетка — может уже не подойти для оценки вероятности события в сложных производственных или социальных процессах.

Наша жизнь сейчас насыщена огромным количеством информации и необходимость иметь инструменты для прогнозирования результатов принятых решений актуальна как никогда. Всего 25–30 лет назад доступные знания размещались на нескольких книжных полках или в лучшем случае в библиотеках для тех, кто имел возможность доступа к ним. Сегодня контент, отображаемый ранее исключительно на бумаге, мгновенно передается по эфиру на наши персональные устройства. Сложные явления по определению трудно объяснять, развивать или прогнозировать. Чтобы осмыслить многочисленные потоки данных, попадающие на наши компьютеры (в промышленности, экономике, социальной жизни), и принять верные решения, нужны именно многочисленные модели для описания процессов, событий и явлений.

Взаимно-однозначный подход при построении моделей и его общие характеристики, озвученные автором книги, можно формализованно представить в виде приведенной ниже схемы.

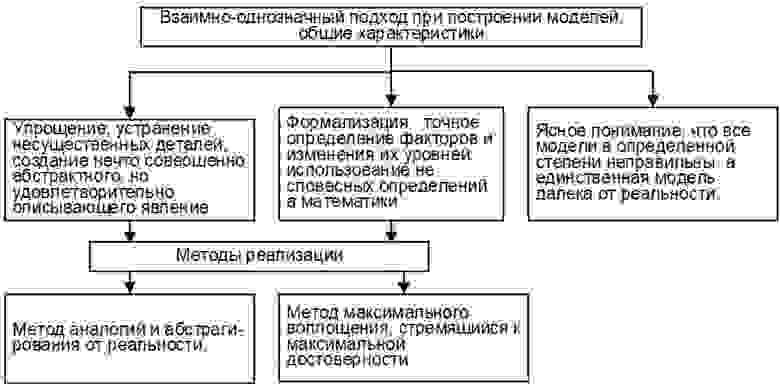
Эти принципы построения моделей могут успешно использоваться и в многомодельном подходе.

Наука о множестве моделей

Автор обосновывает эффективность многомодельного подхода следующим образом (см. схему).

Преимущество, связанное с категоризацией (преимущество моделей, в которых компоненты разбиты на блоки), очень подробно и просто, с многочисленными примерами описано в книге К.А. Браунли (5).

В то же время автор отмечает, что многомодельный подход не всегда идеален. Иногда лучше разработать одну большую модель. Эмпирическое правило звучит так: чем больше у нас данных, тем детализированнее должна быть модель, но до определенного предела. Пример — «Коллегия картографов создала натуральную карту империи, которая была размером с империю и совпадала с ней до единой точки. Потомки, не столь преданные изучению картографии, сочли эту пространную карту бесполезной». К счастью, современная компьютерная техника позволяет достичь подобной детализации, не прибегая к формированию карты размером с оригинал.

К сожалению, доказательство приведенных теорем о необходимости многомодельности у автора книги ограничено лишь словесными рассуждениями и примерами.

Моделирование поведения людей

Непредсказуемость поведения людей представляет проблемы для моделирования. Эти проблемы обусловлены многообразием характеров, желаний людей, агентивностью (способностью действовать, меняться и обучаться).

В книге приводится возможная классификация моделей поведения, которые строятся с учетом указанных проблем.

Модель рационального агента предполагает, что люди делают оптимальный выбор с учетом функции выигрыша или полезности — выбирают действие, максимизирующее полезность.
Mодели, основанные на правилах, предполагают определенное поведение. Правила поведения могут быть фиксированными (применение одного и того же алгоритма во всех случаях) или адаптивными (такое правило подразумевает переключение между вариантами наборов поведения, развитие новых типов поведения или копирование поведения других).
Модели на основе оценки о прошлом поведении людей. Иногда подобные оценки могут быть неточными, нужно учитывать, как именно сегодня люди отреагируют на политические и экологические изменения.

Две последние модели интуитивно понятны, а на модели рационального агента стоит остановиться и порассуждать подробнее, так как в книге в модели рационального агента о функции полезности только упоминается.

Строгое определение этой функции звучит так (6): «каждому предполагаемому результату возможного действия Р обязательно соответствует некоторое число u (P), называемое полезностью действия Р».

Свойства функции полезности:

и (Р1) > u (P2) тогда и только тогда, когда принимающий решение предпочитает Р1, а не Р2. Иными словами, если значение функции Р1 больше, то надо принимать решение по варианту Р1.
Если Р есть предполагаемый результат возможных действий, что с вероятностью р этот предполагаемый результат будет Р1, а с вероятностью (1 — р) он будет Р2, то тогда u (P) = pu (P1)+(1-p)u (P2).

Это последнее уравнение очень простое. Смысл его в том, что суммарная полезность при принятии решений есть сумма отдельных полезностей, каждая из которых выступает со своей вероятностью p, в долях единицы. Полезность может выражаться в количественных единицах, например, денежных, или в виде качественных факторов. На практике применение уравнения может встретить трудности — очень непросто количественно оценить отдельные составляющие и построить суммарную функцию полезности.

Яркий пример — принятие решения о покупке автомашины. Полезность автомашины как транспортного средства, предоставляющего значительные удобства, не вызывает сомнения, однако надо рассматривать и другие «полезности», связанные с этим приобретением. Надо решить вопрос о цене покупки (по силам ли она), вопрос с местом хранения, парковкой, учесть расходы на бензин и обслуживание, решить, как часто ездить — на работу или только на дачу и на рынок, и в первом случае возникает проблема с пробками, наконец, нужно учесть и возможность ДТП. Для некоторых полезностью может служить также вопрос престижа владения дорогим транспортным средством (я не рассматриваю как полезность аргумент «я так хочу»). Следовательно, некоторые «полезности» могут быть и отрицательными, поэтому и суммарная полезность может оказаться отрицательной величиной и принимать данное решение нежелательно.

Таким образом, в качестве «полезности» мы должны рассматривать не одно отдельно взятое преимущество, связанное с принятием данного решения, а полезность в целом, как функцию суммы всех «полезностей» с их вероятностями (или долями). Перечень полезностей и ранжирование их определять нужно самостоятельно либо с помощью экспертных оценок.

Вряд ли кто-нибудь из нас при принятии сложного решения с далеко идущими последствиями будет составлять функцию полезности, но понимать, что требуется четко ранжировать все факторы по их направленности и вкладу в возможные последствия — совершенно необходимо.

Практическое применение моделей, которые приводятся в последующих главах книги, без расчета функции их полезности рассматривать затруднительно.

Построим модель

Главы с 7 по 29 книги содержат описание методов принятия решений с помощью моделей применительно к самым различным областям человеческой деятельности, преимущественно бытовой. Совершенно невозможно дать краткое изложение всего приведенного в этих главах, поэтому вынужден выполнить некоторую общую систематизацию существующего перечня процессов, которые являются предметом для моделирования в различных областях.

Модели физических и производственных процессов (физико-химические, производственно-технологические). Подобные процессы в книге не рассматриваются, примеры моделирования их можно найти в работах академика В.В. Кафарова (7).
Модели, связанные с играми, балансом популяций, некоторые из которых рассмотрены в книге. Сюда же можно отнести модели экономические (в книге они рассматриваются с бытовых позиций).

Привожу пример экономической модели (8) из области экономики предприятия — зависимость затрат на один рубль валовой продукции в неизменных ценах на планируемый год:

$С= 0,409П^{0,26} *Тп^{0,454} *Та^{0,113} *уз^{0,079} *уо^{0,162} *\frac{уа^{0,003}}{ В^{0,213}} *[\frac{v}{(c+v)}]^{0,106} *Д^{0.082}$

где П — стоимость производственных фондов; Тп — темп роста производственных фондов; у3 — удельный вес заработной платы; уо — удельный вес оборотных фондов в производственных фондах; уа — удельный вес активной части производственных фондов; В — валовая продукция базисного года, тыс. руб; Д — длительность производственного цикла базисного года в % (оцените простоту формулы!).

Эмпирические модели, используемые для подгонки эмпирических данных и математического планирования экспериментов (9). В книге они также не рассмотрены.

Блок-схема шагов, необходимых для построения моделей при решении технико-экономических задач, которая пригодна и для построения простейших моделей, типа приведенных в рассматриваемой нами книге, представлена ниже.

В сухом остатке

В целом книгу читать интересно, хотя по сравнению с уровнем опубликованных в конце XX века работ на данную тему она выглядит несколько слабовато. Для подтверждения своих слов могу сослаться на уже упомянутую переводную работу Г. Чернова и Л. Мозеса, которая практически аналогична по содержанию, но уровень изложения в ней заметно более четкий.

Книга также не является настольным руководством по разработке моделей. Она лишь приводит примеры многочисленных инструментов, которые можно использовать при разработке моделей, описывающих то или иное событие, явление. Читателю предлагается самому решать, как строить модели с помощью этих инструментов.

Источники

Вильямс Дж. Д. «Совершенный стратег или букварь по теории стратегических игр» («Советское радио», М., 1960, 266 с.).
Чернов Г., Мозес Л. «Элементарная теория статистических решений» («Советское радио», М. 1962, 406 с.).
Химмельблау Д. «Анализ процессов статистическими методами» («Мир», М. 1973, 957 с.).
Вознесенский В. А., Ковальчук А.Ф. Принятие решений по статистическим моделям («Статистика», М., 1978 г., 192 с.).
Браунли К. А. «Статистические исследования в производстве» («Иностранная литература», М., 1949, 227 с.).
Чернов Г., Мозес Л. «Элементарная теория статистических решений» («Советское радио», М. 1962, 88 с.).
Кафаров В. В. «Моделирование химических процессов» («Знание», М., 1968).
Венецкий И. Г. «Основные математико-статистические понятия и формулы в экономическом анализе» («Статистика», М., 1979 г., 448 с.)
Налимов В. В., Чернова Н. А. «Статистические методы планирования экстремальных экспериментов» («Наука», М., 1965 г., 340 с.).