Учиться, учиться, и ещё раз учиться?01.06.2021 15:01

TLDR: крохотные модельки обошли модные графовые нейронки в предсказании свойств молекул.
Код: здесь. Берегите Природу.

ФОТО: Андерс Хеллберг для Wikimedia Commons, модель — Грета Тунберг

Необученная графовая свёрточная нейронная сеть [1] (uGCN) со случайной инициализацией весов уже пару лет занимает первое место в моём списке алгоритмов для задач машинного обучения на графах из-за копеечной стоимости, простоты реализации, да вполне очевидной элегантности решения. В то же время, насколько мне известно, никто ещё не не проводил соревнований между этой простой моделью и её старшей сестрой — полноценно обученной графовой свёрточной нейронной сетью (GCN) в режиме обучения с учителем. Вот я сделал.

Мотивация: показать, что uGCN выдаёт качественные представления, которые можно использовать в последующих задачах машинного обучения в индуктивном режиме, когда модели обобщаются к не виденным ранее данным (вдохновлено недавним отчётом [2] о производительности простых моделей в трансдуктивном случае).

Полученные результаты — занимательны. В худшем случае простые модели (uGCN + degree kernel + random forest) показали счёт 54:90 против полноценно обученных GCN, в то время как реалистичный сценарий закончился разгромным реваншем 93:51, указывающим на то, что мы можем позволить себе почти бесплатные эмбеддинги, которые превосходят или показывают результаты на уровне полноценно обученных GCN в задаче предсказания свойств графа (например — эффекта медикаментов: яд или лекарство) за долю стоимости. Простые модели обучались ~10 минут в то время как весь эксперимент продлился ~4 часа. Перейдём же к деталям и разберёмся с тем, что произошло!

Основные понятия

Многие из важных наборов данных об окружающем нас мире имеют связный характер: социальные сети, графы знаний, взаимодействия белков, всемирная паутина WWW и т.д. (просто несколько примеров) [1].

Граф, обыкновенно записываемый как G=(V, E) — это математическая модель, множество множеств, состоящее из набора вершин V и множества рёбер E — попарных связей e (i, j) между вершинами i и j. Расширением Графа является модель Граф со Свойствами (Labeled Property Graph), позволяющий задать вектор признаков xi для вершины i (мы также можем определять свойства для рёбер, однако это выходит за рамки сегодняшнего эксперимента). Графовая нейронная сеть [3] (GNN) — это модель машинного обучения (параметрическая функция, которая подбирает, другими словами — выучивает, параметры из данных), расширяющая возможности хорошо известного семейства алгоритмов, вдохновлённых биологией, до работы с неструктурированными данными в виде графов. На мой взгляд, передача сообщений — это самая простая интуиция для понимания механики работы GNN и вполне оправдано обратиться к мнемоническому правилу 'скажи мне, кто твой друг и я скажу тебе кто ты'. Графовые свёрточные нейронные сети (GCN) очень подробно описал их изобретатель здесь (https://tkipf.github.io/graph-convolutional-networks/) и мне, право, непросто что-то ещё добавить к этой замечательной истории.

Дабы не заниматься самоцитированием, предложу читателю ознакомиться с рассказом о том, где и как врубиться в эмбеддинги графов, а также — с примером использования GCN в структурном моделировании организационных изменений и ощущениях стейкхолдеров во время кадровых перестановок, неизбежных при внедрении больших информационных систем, вроде SAP. Эти два текста стоит воспринимать как первые главы повествования о методах анализа связанных систем, также там в деталях рассматривается используемая форма математической записи.

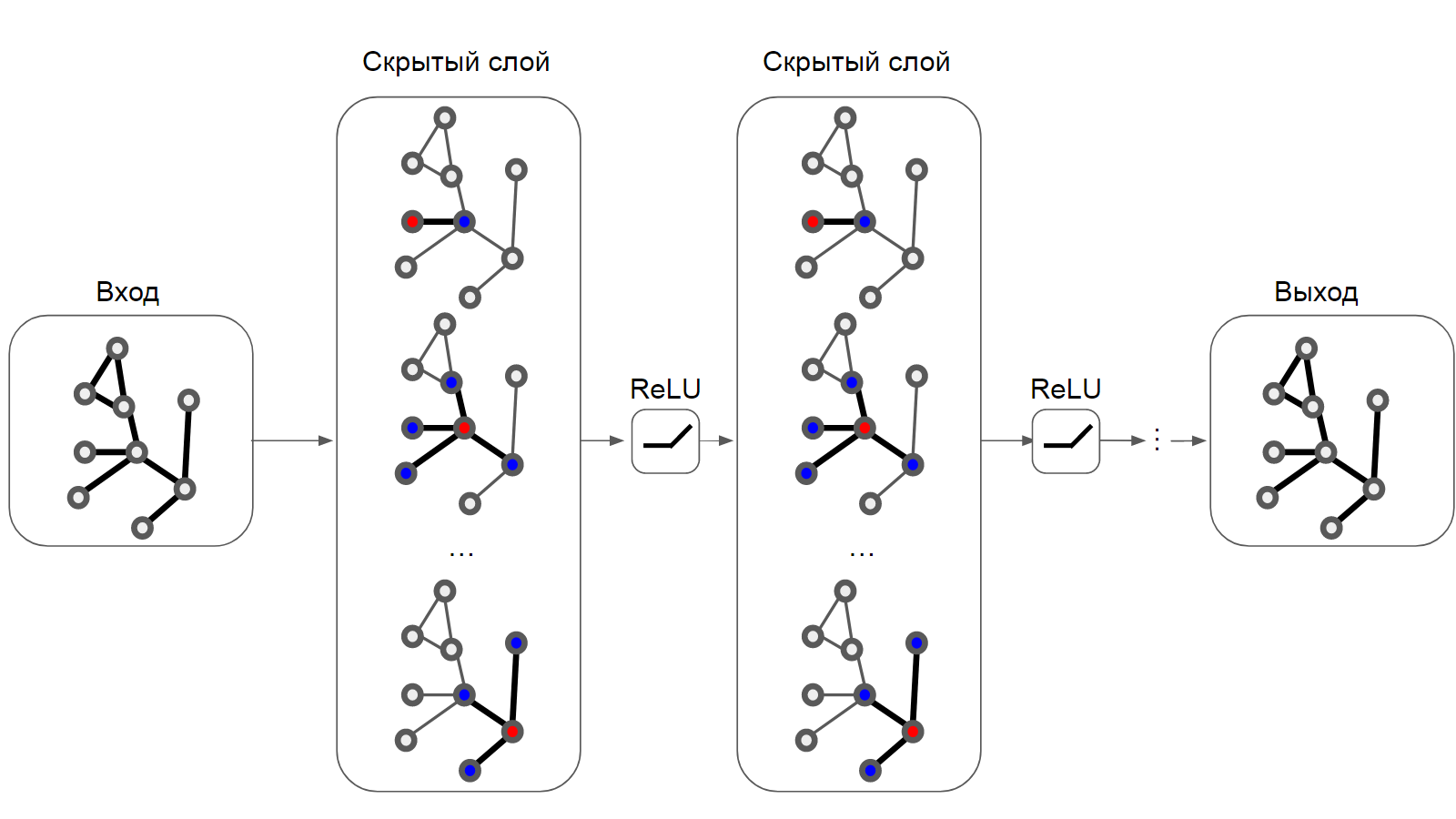
Многослойная GCN с фильтрами первого порядка.

Данные

Проведём серию экспериментов на общедоступных данных. Мы обратимся к (i) коллекции TUDatasets [4] и (ii) ограничим наше упражнение задачей бинарной классификации (предсказанием свойств) небольших молекул. Ещё одним условием нашего мероприятия будет (iii) использование графов с признаками вершин.

Заданные ограничения оставляют нам несколько наборов данных, широко используемых для сравнения современных алгоритмов. Вот наш итоговый список: AIDS, BZR, COX2, DHFR, MUTAG и PROTEINS. Все обозначенные наборы данных доступны как часть Pytorch Geometric [5] (библиотека для глубокого обучения на графах) в двух версиях: оригинальной и очищенной от дубликатов [6]. Итого у нас будет 12 датасетов.

AIDS Antiviral Screen Data [7]

Результаты экспериментов по выявлению химических соединений, негативно влияющих на вирус иммунодефицита человека. Представляет собой результат тестирования и химическую структуру соединений не покрытых соглашениями о неразглашении. В оригинальном наборе содержится 2000 молекул, а очищенная версия оставляет нам 1110 точек данных, каждая из которых представляет собой граф, вершины которого описывают 37 признаков.

Benzodiazepine receptor (BZR) ligands [8]

Оригинальный набор содержит 405 молекул, очищенная версия — 276, по 35 признаков на вершину.

Cyclooxygenase-2 (COX-2) inhibitors [8]

Оригинальный набор содержит 467 молекул, очищенная версия — 237, по 35 признаков на вершину.

Dihydrofolate reductase (DHFR) inhibitors [8]

Оригинальный набор содержит 756 молекул, очищенная версия — 578, 35 признаков на вершину.

MUTAG [9]

В наборе содержится 188 химических соединений, разделённых на два класса согласно их мутагенному воздействию на бактерии. В очищенной версии — 135 молекул, 7 признаков на вершину.

PROTEINS [10]

Энзимы и не-энзимы. В оригинальном наборе содержится 1113 молекул, по 3 признака на вершину. Очищенная версия — 975 структур.

Дизайн Эксперимента

Мы устроим турнир!

Для каждого набора данных проведём 12 раундов обучения и тестирования.

В каждом раунде:

(1) псевдослучайным образом разделим данные в пропорции 80/20 в Pytorch Geometric (начиная со стартового параметра генератора random seed = 42 и увеличивая его на единицу в каждом последующем раунде), таким образом 80% точек данных (графов) будут использованы в качестве обучающей выборки, а оставшиеся 20% — будут тестовой выборкой;

(2) обучим модели и оценим долю верных ответов (accuracy) на тесте.

Для простых моделей это значит предобработку для того, чтобы создать признаки, на которых будет обучен классификатор.

Для GCN мы проводим 200 эпох обучения и тестирования со скоростью обучения learning rate = 0.01 и принимаем во внимание:
(А) среднее значение доли верных ответов для 10 финальных эпох обучения — реалистичный сценарий;
(В) наибольшее значение доли верных ответов, достигнутое в процессе обучения (как если бы мы сохраняли промежуточное состояние для того, чтобы выбрать наилучшую модель впоследствии) — наилучший сценарий для GCN (и наихудший для простых моделей);

(3) лучшей модели присуждается 1 балл;

(4) в случае ничьей балл присуждается лёгкой модели.

Всего будет распределено 288 баллов: 12 датасетов 12 раундов 2 сценария.

Модели

Degree kernel (DK) или степенное ядро — гистограмма степеней вершин (количество рёбер, соединённых с вершиной), нормированная к числу вершин в графе (таким образом вектор признаков для каждого графа состоит из размеров долей вершин с количеством связей, равным индексу признака, от всего множества вершин — в сумме они дают единицу).

import networkx as nx
import numpy as np 
from scipy.sparse import csgraph
# g - граф формате популярной библиотеки NetworkX
numNodes = len(g.nodes)
degreeHist = nx.degree_histogram(g)
# нормализуем
degreeHist = [x/numNodes for x in degreeHist]

Необученная графовая свёрточная нейронная сеть (uGCN) со случайной инициализацией весов — 3 слоя с промежуточной нелинейной активацией (ReLU, т.е. f (x) = max (x, 0)). Аггрегация усреднением полученных после прямого прохода 64-разрядных векторов (эмбеддинги вершин) позволяет получить компактное представление графа. Это на самом деле очень просто.

A = nx.convert_matrix.to_scipy_sparse_matrix(g)

Воспользуемся вариантом реализации одного слоя свёртки в три строки, который пару лет назад предложил iggisv9t:

# A - матрица связности графа
# X - матрица признаков вершин (np.array)
D = sparse.csgraph.laplacian(A, normed=True)
shape1 = X.shape[1]
X = np.hstack((X, (D @ X[:, -shape1:])))

(код здесь приводится чтобы подчеркнуть очаровательный минимализм реализации метода)

Разберём его на части и пересоберём заново.

Использованная реализация uGCN выглядит так:

# A - матрица связности графа
# X - матрица признаков вершин (np.array)
# W0, W1, W2 - случайным образом инициализированные веса
D = sparse.csgraph.laplacian(A, normed=True)
# слой 0
Xc = D @ X @ W0
# ReLU
Xc = Xc * (Xc>0)
# конкатенация признаков вершин с аггрегированной информацией соседей
Xn = np.hstack((X, Xc))
# слой 1
Xc = D @ Xn @ W1
# ReLU
Xc = Xc * (Xc>0)
Xn = np.hstack((Xn, Xc))
# слой 2 - эмбеддинги вершин
Xc = D @ Xn @ W2
# аггрегация усреднением - эмбеддинг графа
embedding = Xc.sum(axis=0) / Xc.shape[0]

Комбинация DK и uGCN (Mix) — конкатенацией представлений графа, полученных с помощью моделей DK и uGCN.

mix = degreeHist + list(embedding)

Для каждой из первых трёх моделей обучаем классификатор — случайный лес из 100 деревьев с максимальной глубиной в 17 ветвлений.

Графовая свёрточная нейронная сеть (GCN) — полноценно обученный классификатор, состоящий из 3 свёрточных слоёв размерностью 64 с промежуточной нелинейной активацией (ReLU), агрегацией усреднением (до этого момента архитектура GCN очень похожа на uGCN), за которой следует слой регуляризации дропаутом (произвольным обнулением разрядов с вероятностью 50%) и линейный классификатор. Мы будем обозначать результаты модели, отобранные в наилучшем для GCN сценарии (B) как GCN-B, а модели в реалистичном сценарии (А) как GCN-A.

Результаты

После 144 раундов (12 датасетов * 12 раундов) сравнения качества предсказаний на отложенной выборке между простыми моделями и полноценно обученными графовыми свёрточными сетями 288 баллов распределились как:

147:141

Доля верных ответов на тестовых выборках варьировалась между раундами и частенько случались ситуации, в которых простые модели доминировали над более сложными противниками.

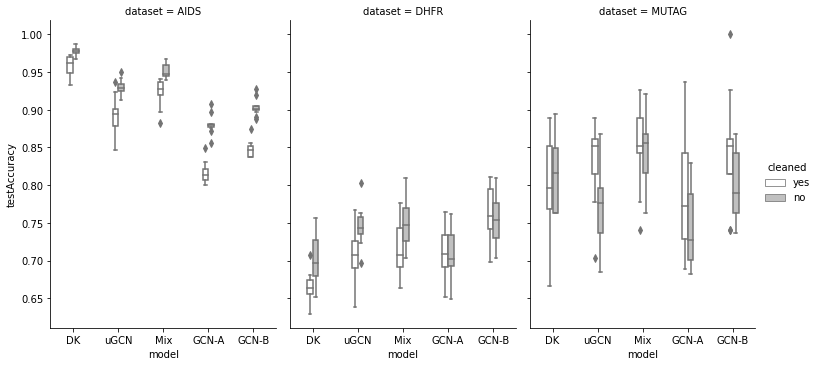
Наборы данных, в которых простые модели побеждают: AIDS, DHFR (A) и MUTAG.

Например, DK собрала все 48 баллов для набора данных AIDS, демонстрируя отрыв более чем на 10% (абсолютное значение) от доли верных ответов полноценно обученной GCN.

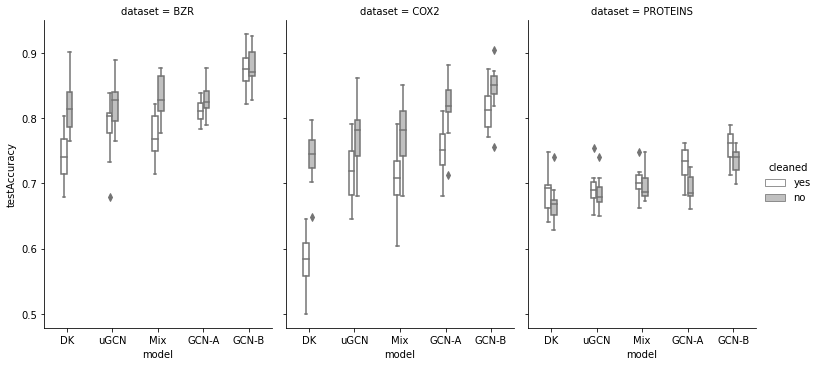
Здесь побеждают GCN: BZR, COX2 и PROTEINS.

Индивидуальный зачёт:
90 — GCN-B;
71 — DK;
55 — Mix (uGCN + DK);
51 — GCN-A;
21 — uGCN.

Достаточно подробный протокол соревнований приведён в блокнотике с кодом, таблица с результатами раундов — здесь.

В целом, результаты стабильно варьировались между очищенными и оригинальными наборами данных. Это ещё раз напоминает о важности качества данных для проведения адекватных сравнений между моделями. Хорошая новость в том, что в исследовательском сообществе уже есть движение в данном направлении и значительные усилия лучших умов в области уже направлены на организацию честных турниров.

Выводы

Как видим, проведенный эксперимент подтверждает предположение о том, что в задаче предсказания свойств молекул мы можем позволить себе использовать почти бесплатные эмбеддинги, которые превосходят или показывают результаты на уровне полноценно обученных нейронных сетей. Наблюдения согласуются с вдохновляющими этот эксперимент результатами [2] в том, что концептуально метод Label Propagation очень похож на передачу сообщений в графовой свёрточной нейронной сети. Объяснение эффективности скорее всего следует искать в том, что на самом деле мощнее — подбирать параметры фильтров для того, чтобы внутренние представления, выученные сетью стали линейно разделимыми, либо же просто использовать классификатор помощнее, как это сделано в рассмотренном примере.

Дисперсия результатов между раундами соревнования напоминает о том, что всякое сравнение — дело непростое. Здесь стоит упомянуть Free Lunch Theorem и напомнить о том, что использовать сразу несколько моделей в построении решения — скорее хороший тон. Также важно отметить влияние разбиения на выборки в ходе сравнения — на одном и том же наборе данных одна и та же модель может показывать очень разное качество. Поэтому сравнивая модели, убедитесь, что обучаете и тестируете их на идентичных выборках. К слову, фиксация параметров генератора псевдослучайных чисел — не панацея…

Дальнейшими шагами может быть сравнение производительности моделей в рамках наборов данных больших размеров. Также стоит проверить результаты и в других задачах, таких как: предсказание связи, классификация вершин, регрессия на графах, и прочих — графовые нейронные сети (как обученные, так и просто так) — на многое способны.

Послесловие

В лекции открытого курса по графам знаний GCN названа Королевской Лазейкой Через Пространство Фурье, этот ярлык приклеился с тех пор, когда впервые выступил на публике с рассказом о силе графов и провёл первые эксперименты с классификацией картинок (как графов) для того, чтобы продемонстрировать мощь спектральных фильтров одной юной леди, запускавшей стартап в милой моему сердцу аэрокосмической области. Данная заметка появилась в результате того, что пару недель назад в реальной задаче на закрытых данных uGCN, вместе с простенькими моделями показали результат, который полноценно обученные GCN смогли превзойти всего на 2% (96 против 98) и мне вздумалось проверить вопрос о том, кто кого заборет ещё на каких-нибудь данных.

В наши дни машинное обучение на графах превратилось в знаменитость, всё больше исследователей обращают внимание на эту область и новые архитектуры графовых нейронных сетей появляются каждую неделю. Однако на самом деле мы ещё не очень хорошо понимаем почему GNN так успешны и нужны ли они для хорошего качества решения [2].

Перед тем, как ступать на очаровательный путь машинного обучения на графах, пожалуйста ознакомьтесь с основами этого дела. Значительные усилия прилагаются к тому, чтобы сделать новейшие достижения (да и классические методы тоже) доступными широкой аудитории совершенно бесплатно. Упомяну лишь несколько из таких инициатив: материалы и лекции стенфордского cs224w, площадку для тестирования качества алгоритмов Open Graph Benchmark [14] и недавнюю работу об основах геометрического глубокого обучения [15] — методологию разработки новых архитектур нейронных сетей. Напоследок, ещё раз напомню о том, что начинать проекты машинного обучения стоит с простых методов, вроде ядер и необученных графовых свёрточных сетей — достаточно часто эти модельки показывают неприлично хороший уровень.

Берегите Природу, используйте алгоритмы эффективно. Порою неученье — сила.

Литература

[1] Kipf & Welling, Semi-Supervised Classification with Graph Convolutional Networks (2017), International Conference on Learning Representations;
[2] Huang et al., Combining Label Propagation and Simple Models out-performs Graph Neural Networks (2021), International Conference on Learning Representations;
[3] Scarselli et al., The Graph Neural Network Model (2009), IEEE Transactions on Neural Networks (Volume: 20, Issue: 1, Jan. 2009);
[4] Morris et al., TUDataset: A collection of benchmark datasets for learning with graphs (2020), ICML 2020 Workshop on Graph Representation Learning and Beyond;
[5] Fey & Lenssen, Fast Graph Representation Learning with PyTorch Geometric (2019), ICLR Workshop on Representation Learning on Graphs and Manifolds;
[6] Ivanov, Sviridov & Burnaev, Understanding isomorphism bias in graph data sets (2019), arXiv preprint arXiv:1910.12091;
[7] Riesen & Bunke, IAM Graph Database Repository for Graph Based Pattern Recognition and Machine Learning (2008), In: da Vitora Lobo, N. et al. (Eds.), SSPR&SPR 2008, LNCS, vol. 5342, pp. 287–297;
[8] Sutherland et al., Spline-fitting with a genetic algorithm: a method for developing classification structure-activity relationships (2003), J. Chem. Inf. Comput. Sci., 43, 1906–1915;
[9] Debnath et al., Structure-activity relationship of mutagenic aromatic and heteroaromatic nitro compounds (1991), J. Med. Chem. 34(2):786–797;
[10] Dobson & Doig, Distinguishing enzyme structures from non-enzymes without alignments (2003), J. Mol. Biol., 330(4):771–783;
[11] Pedregosa et al., Scikit-learn: Machine Learning in Python (2011), JMLR 12, pp. 2825–2830;
[12] Waskom, seaborn: statistical data visualization (2021), Journal of Open Source Software, 6(60), 3021;
[13] Hunter, Matplotlib: A 2D Graphics Environment (2007), Computing in Science & Engineering, vol. 9, no. 3, pp. 90–95;
[14] Hu et al., Open Graph Benchmark: Datasets for Machine Learning on Graphs (2020), arXiv preprint arXiv:2005.00687;
[15] Bronstein et al., Geometric Deep Learning: Grids, Groups, Graphs, Geodesics, and Gauges (2021), arXiv preprint arXiv:2104.13478.