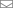The authoritative guide to Blockchain Sharding
Hi, I’m one of the developers of the sharded blockchain Near Protocol, and in this article want to talk about what blockchain sharding is, how it is implemented, and what problems exist in blockchain sharding designs.
It is well-known that Ethereum, the most used general purpose blockchain at the time of this writing, can only process less than 20 transactions per second on the main chain. This limitation, coupled with the popularity of the network, leads to high gas prices (the cost of executing a transaction on the network) and long confirmation times; despite the fact that at the time of this writing a new block is produced approximately every 10–20 seconds the average time it actually takes for a transaction to be added to the blockchain is 1.2 minutes, according to ETH Gas Station. Low throughput, high prices, and high latency all make Ethereum not suitable to run services that need to scale with adoption.
What is the primary reason for Ethereum«s low throughput? The reason is that every node in the network needs to process every single transaction. Developers have proposed many solutions to address the issue of throughput on the protocol level. These solutions can be mostly separated into those that delegate all the computation to a small set of powerful nodes, and those that have each node in the network only do a subset of the total amount of work. An extreme case of the former approach is Thunder that has one single node processing all the transactions and claims to achieve 1200 tx/sec, a 100x improvement over Ethereum (I do not, however, endorse Thunder, or attest to the validity of their claims). Algorand, SpaceMesh, Solana all fit into the former category, building various improvements in the consensus and the structure of the blockchain itself to run significantly more transactions, but still bounded by what a single (albeit very powerful) machine can process.
The latter approach, in which the work is split among all the participating nodes, is called sharding. This is how Ethereum Foundation currently plans to scale Ethereum. At the time of this writing the full spec is still not published. Here are links to a detailed overview of Ethereum shard chains and the Beacon chain.
In this post I summarize the core ideas of blockchain sharding, on which both Near and majority of other sharded protocols are based. The subsequent post will outline more advanced topics in sharding.
The simplest Sharding, a.k.a. Beanstalk
Let«s start with the simplest approach to sharding, that we throughout this write-up will call a Beanstalk. This is also what Vitalik calls «scaling by a thousand altcoins» in this presentation.
In this approach instead of running one blockchain, we will run multiple, and call each such blockchain a «shard». Each shard will have its own set of validators. Here and below we use a generic term «validator» to refer to participants that verify transactions and produce blocks, either by mining, such as in Proof of Work, or via a voting-based mechanism. For now let«s assume that the shards never communicate with each other.
The Beanstalk design, though simple, is sufficient to outline some major challenges in sharding.
Validator partitioning and Beacon chains
The first challenge is that with each shard having its own validators, each shard is now 10 times less secure than the entire chain. So if a non-sharded chain with X validators decides to hard-fork into a sharded chain, and splits X validators across 10 shards, each shard now only has X/10 validators, and corrupting one shard only requires corrupting 5.1% (51% / 10) of the total number of validators.
Which brings us to the second point: who chooses validators for each shard? Controlling 5.1% of validators is only damaging if all those 5.1% of validators are in the same shard. If validators can«t choose which shard they get to validate in, a participant controlling 5.1% of the validators is highly unlikely to get all their validators in the same shard, heavily reducing their ability to compromise the system.
Almost all sharding designs today rely on some source of randomness to assign validators to shards. Randomness on blockchain on itself is a very challenging topic and would deserve a separate blog post at some later date, but for now let«s assume there«s some source of randomness we can use.
Both the randomness and the validators assignment require computation that is not specific to any particular shard. For that computation, practically all existing designs have a separate blockchain that is tasked with performing operations necessary for the maintenance of the entire network. Besides generating random numbers and assigning validators to the shards, these operations often also include receiving updates from shards and taking snapshots of them, processing stakes and slashing in Proof-of-Stake systems, and rebalancing shards when that feature is supported. Such chain is called a Beacon chain in Ethereum and Near, a Relay chain in PolkaDot, and the Cosmos Hub in Cosmos.
Throughout this post we will refer to such chain as a Beacon chain. The existence of the Beacon chain brings us to the next interesting topic, the quadratic sharding.
Quadratic sharding
Sharding is often advertised as a solution that scales infinitely with the number of nodes participating in the network operation. While it is in theory possible to design such a sharding solution, any solution that has the concept of a Beacon chain doesn«t have infinite scalability. To understand why, note that the Beacon chain has to do some bookkeeping computation, such as assigning validators to shards, or snapshotting shard chain blocks, that is proportional to the number of shards in the system. Since the Beacon chain is itself a single blockchain, with computation bounded by the computational capabilities of nodes operating it, the number of shards is naturally limited.
However, the structure of a sharded network does bestow a multiplicative effect on any improvements to its nodes. Consider the case in which an arbitrary improvement is made to the efficiency of nodes in the network which will allow them faster transaction processing times.
If the nodes operating the network, including the nodes in the Beacon chain, become four times faster, then each shard will be able to process four times more transactions, and the Beacon chain will be able to maintain 4 times more shards. The throughput across the system will increase by the factor of 4×4 = 16 — thus the name quadratic sharding.
It is hard to provide an accurate measurement for how many shards are viable today, but it is unlikely that in any foreseeable future the throughput needs of blockchain users will outgrow the limitations of quadratic sharding. The sheer number of nodes necessary to operate such a volume of shards securely is orders of magnitude higher than the number of nodes operating all the blockchains combined today.
However, if we want to build future proof protocols, it might be worth starting researching solutions to this problem today. The most developed proposal as of now is exponential sharding, in which shards themselves are forming a tree, and each parent shard is orchestrating a series of child shards, while can itself be a child of some other shard.
Vlad Zamfir from Ethereum Foundation is known to be working on a sharding design that doesn«t involve a beacon chain; I worked with him on one of the prototypes, the detailed overview of which is here.
State Sharding
Up until now we haven«t defined very well what exactly is and is not separated when a network is divided into shards. Specifically, nodes in the blockchain perform three important tasks: not only do they 1) process transactions, they also 2) relay validated transactions and completed blocks to other nodes and 3) store the state and the history of the entire network ledger. Each of these three tasks imposes a growing requirement on the nodes operating the network:
- The necessity to process transactions requires more compute power with the increased number of transactions being processed;
- The necessity to relay transactions and blocks requires more network bandwidth with the increased number of transactions being relayed;
- The necessity to store data requires more storage as the state grows. Importantly, unlike the processing power and network, the storage requirement grows even if the transaction rate (number of transactions processed per second) remains constant.
From the above list it might appear that the storage requirement would be the most pressing, since it is the only one that is being increased over time even if the number of transactions per second doesn«t change, but in practice the most pressing requirement today is the compute power. The entire state of Ethereum as of this writing is 100GB, easily manageable by most of the nodes. But the number of transactions Ethereum can process is around 20, orders of magnitude less than what is needed for many practical use cases.
Zilliqa is the most well-known project that shards processing but not storage. Sharding of processing is an easier problem because each node has the entire state, meaning that contracts can freely invoke other contracts and read any data from the blockchain. Some careful engineering is needed to make sure updates from multiple shards updating the same parts of the state do not conflict. In those regards Zilliqa is taking a very simplistic approach, criticism of which can be found in this post.
While sharding of storage without sharding of processing was proposed, I«m not aware of any project working on it. Thus in practice sharding of storage, or State Sharding, almost always implies sharding of processing and sharding of network.
Practically, under State Sharding the nodes in each shard are building their own blockchain that contains transactions that affect only the local part of the global state that is assigned to that shard. Therefore, the validators in the shard only need to store their local part of the global state and only execute, and as such only relay, transactions that affect their part of the state. This partition linearly reduces the requirement on all compute power, storage, and network bandwidth, but introduces new problems, such as data availability and cross-shard transactions, both of which we will cover below.
Cross-shard transactions
Beanstalk as a model is not a very useful approach to sharding, because if individual shards cannot communicate with each other, they are no better than multiple independent blockchains. Even today, when sharding is not available, there«s a huge demand for interoperability between various blockchains.
Let«s for now only consider simple payment transactions, where each participant has account on exactly one shard. If one wishes to transfer money from one account to another within the same shard, the transaction can be processed entirely by the validators in that shard. If, however, Alice that resides on shard #1 wants to send money to Bob who resides on shard #2, neither validators on shard #1(they won«t be able to credit Bob«s account) nor the validators on shard #2 (they won«t be able to debit Alice«s account) can process the entire transaction.
There are two families of approaches to cross-shard transactions:
- Synchronous: whenever a cross-shard transaction needs to be executed, the blocks in multiple shards that contain state transition related to the transaction get all produced at the same time, and the validators of multiple shards collaborate on executing such transactions. The most detailed proposal known to me is Merge Blocks, described here.
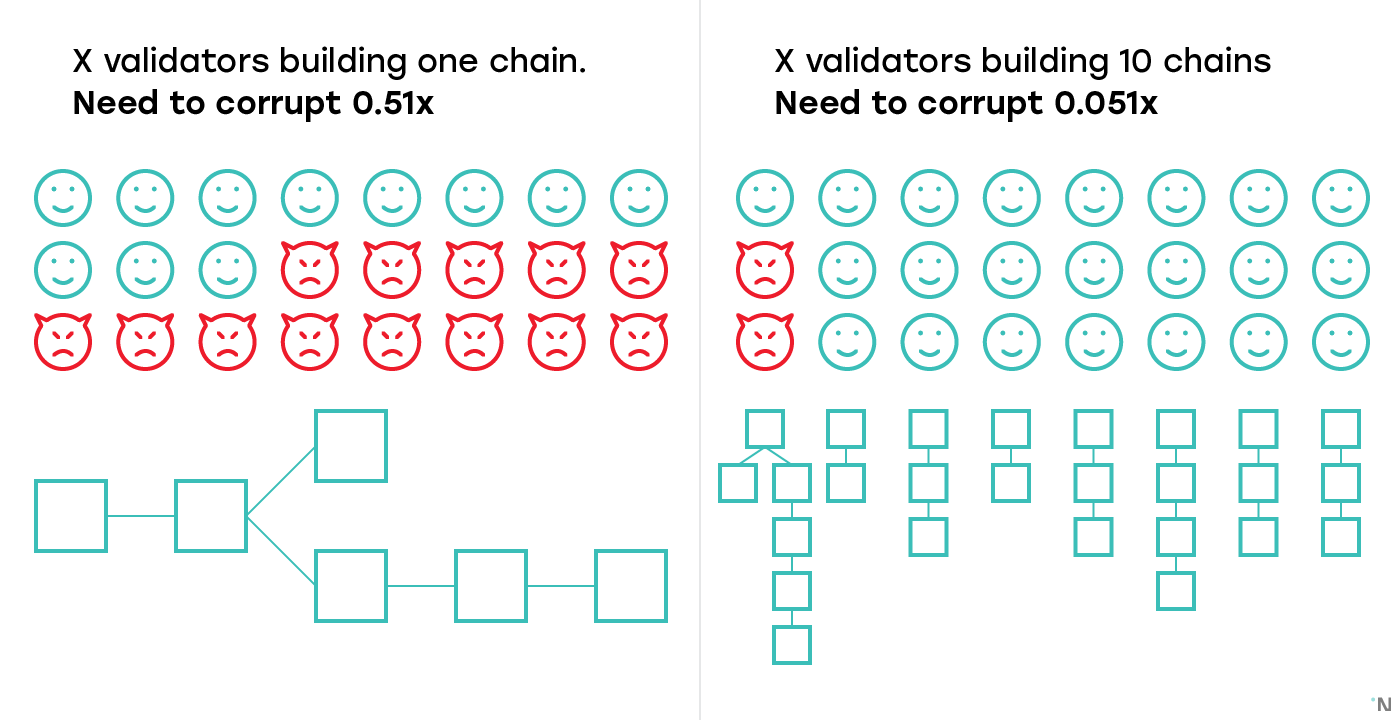
- Asynchronous: a cross-shard transaction that affects multiple shards is executed in those shards asynchronously, the «Credit» shard executing its half once it has sufficient evidence that the «Debit» shard has executed its portion. This approach tends to be more prevalent due to its simplicity and ease of coordination. This system is today proposed in Cosmos, Ethereum Serenity, Near, Kadena, and others. A problem with this approach lies in that if blocks are produced independently, there«s a non-zero chance that one of the multiple blocks will be orphaned, thus making the transaction only partially applied. Consider the figure below that depicts two shards both of which encountered a fork, and a cross-shard transaction that was recorded in blocks A and X» correspondingly. If the chains A-B and V»-X»-Y»-Z» end up being canonical in the corresponding shards, the transaction is fully finalized. If A»-B»-C»-D» and V-X become canonical, then the transaction is fully abandoned, which is acceptable. But if, for example, A-B and V-X become canonical, then one part of the transaction is finalized and one is abandoned, creating an atomicity failure. We will cover how this problem is addressed in proposed protocols in the second part, when covering changes to the fork-choice rules and consensus algorithms proposed for sharded protocols.
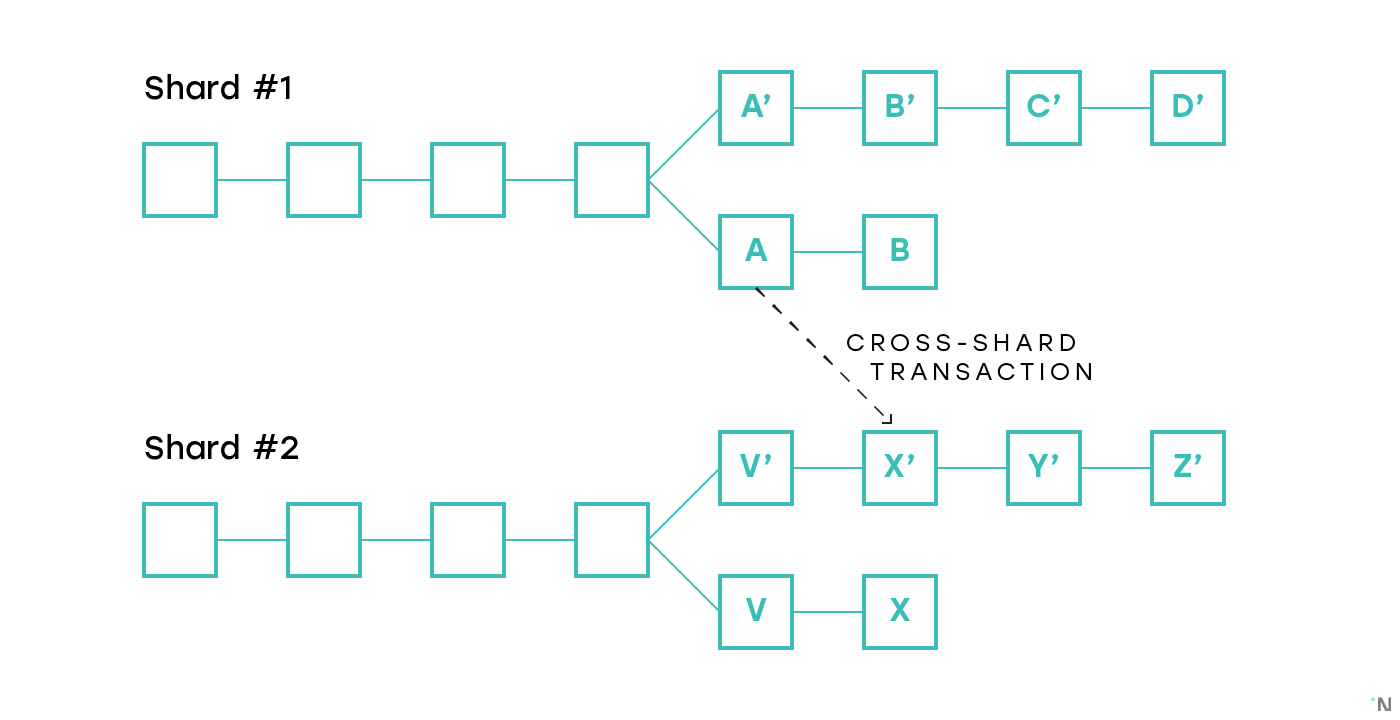
Note that communication between chains is useful outside of sharded blockchains too. Interoperability between chains is a complex problem that many projects are trying to solve. In sharded blockchains the problem is somewhat easier since the block structure and consensus are the same across shards, and there«s a beacon chain that can be used for coordination. In a sharded blockchain, however, all the shard chains are the same, while in the global blockchains ecosystem there are lots of different blockchains, with different target use cases, decentralization and privacy guarantees.
Building a system in which a set of chains have different properties but use sufficiently similar consensus and block structure and have a common beacon chain could enable an ecosystem of heterogeneous blockchains that have a working interoperability subsystem. Such system is unlikely to feature validator rotation, so some extra measures need to be taken to ensure security. Both Cosmos and PolkaDot are effectively such systems. This writeup by Zaki Manian from Cosmos provides detailed overview and comparison of the key aspects of the two projects.
Malicious behavior
You now have a good understanding of how sharding is implemented, including the concepts of the beacon chain, validator rotations and cross-shard transactions.
With all that information, there«s one last important thing to consider. Specifically, what adversarial behavior can malicious validators exercise.
Malicious Forks
A set of malicious validators might attempt to create a fork. Note that it doesn«t matter if the underlying consensus is BFT or not, corrupting sufficient number of validators will always make it possible to create a fork.
It is significantly more likely for more that 50% of a single shard to be corrupted, than for more than 50% of the entire network to be corrupted (we will dive deeper into these probabilities in the second part). As discussed above, cross-shard transactions involve certain state changes in multiple shards, and the corresponding blocks in such shards that apply such state changes must either be all finalized (i.e. appear in the selected chains on their corresponding shards), or all be orphaned (i.e. not appear in the selected chains on their corresponding shards). Since generally the probability of shards being corrupted is not negligible, we can«t assume that the forks won«t happen even if a byzantine consensus was reached among the shard validators, or many blocks were produced on top of the block with the state change.
This problem has multiple solutions, the most common one being occasional cross-linking of the latest shard chain block to the beacon chain. The fork choice rule in the shard chains is then changed to always prefer the chain that is cross-linked, and only apply shard-specific fork-choice rule for blocks that were published since the last cross-link.
Approving invalid blocks
A set of validators might attempt to create a block that applies the state transition function incorrectly. For example, starting with a state in which Alice has 10 tokens and Bob has 0 tokens, the block might contain a transaction that sends 10 tokens from Alice to Bob, but ends up with a state in which Alice has 0 tokens and Bob has 1000 tokens.

In a classic non-sharded blockchain such an attack is not possible, since all the participant in the network validate all the blocks, and the block with such an invalid state transition will be rejected by both other block producers, and the participants of the network that do not create blocks. Even if the malicious validators continue creating blocks on top of such an invalid block faster than honest validators build the correct chain, thus having the chain with the invalid block being longer, it doesn«t matter, since every participant that is using the blockchain for any purpose validates all the blocks, and discards all the blocks built on top of the invalid block.
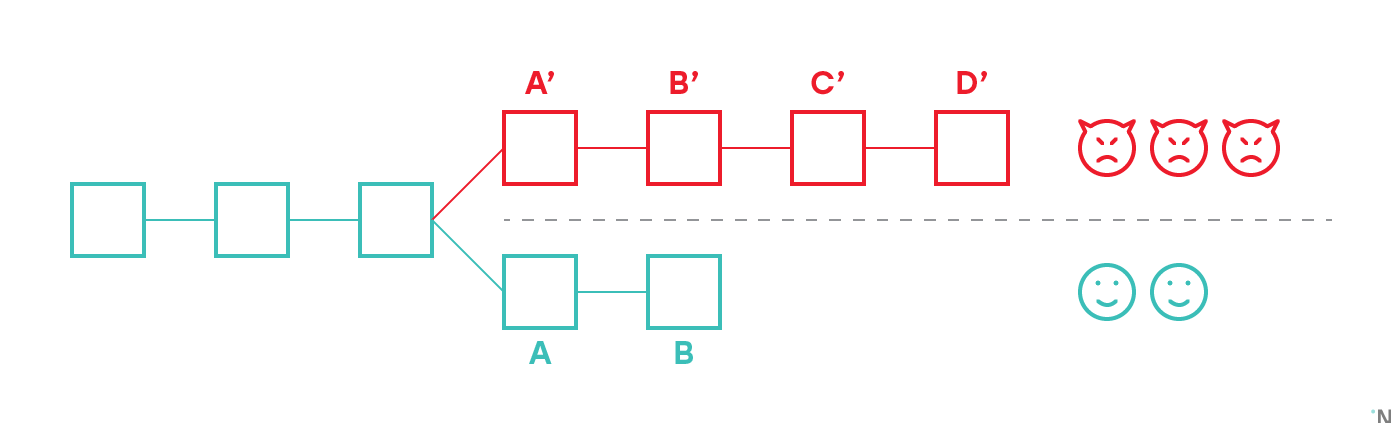
On the figure above there are five validators, three of whom are malicious. They created an invalid block A», and then continued building new blocks on top of it. Two honest validators discarded A» as invalid and were building on top of the last valid block known to them, creating a fork. Since there are fewer validators in the honest fork, their chain is shorter. However, in classic non-sharded blockchain every participant that uses blockchain for any purpose is responsible for validating all the blocks they receive and recomputing the state. Thus any person who has any interest in the blockchain would observe that A» is invalid, and thus also immediately discard B», C» and D», as such taking the chain A-B as the current longest valid chain.
In a sharded blockchain, however, no participant can validate all the transactions on all the shards, so they need to have some way to confirm that at no point in history of any shard of the blockchain no invalid block was included.
Note that unlike with forks, cross-linking to the Beacon chain is not a sufficient solution, since the Beacon chain doesn«t have the capacity to validate the blocks. It can only validate that a sufficient number of validators in that shard signed the block (and as such attested to its correctness).
I am aware of only two solutions to this problem, neither of which is really satisfactory today:
- Have some reasonable mechanism that will alert the system if an attempt to apply the state transition incorrectly is made. Assuming that each shard is running some sort of BFT consensus, for as long as number of malicious validators in a particular shard is less than ⅔, at least one honest validator would need to attest to a block, and verify that the state transition function is applied correctly. If more than ⅔ of the nodes are malicious, they can finalize a block without a single honest node participating. Assuming that at least one node in the shard is not malicious, some mechanism is needed that would allow such nodes to monitor what blocks are being produced, and have sufficient time to challenge nodes with invalid state transition.
- Have some information in the blocks that is sufficient to prove that the state transition is applied correctly but is significantly cheaper to validate than the actual application of the state transition function. The closest mechanism to achieve that is zk-SNARKs (though we don«t really need the «zk», or zero-knowledge, part, a non-zk SNARK would be sufficient), but zk-SNARKs are notoriously slow to compute at this point.
Many protocols today assume that with proper validator rotation and a byzantine fault tolerant consensus neither forks nor invalid state transitions are possible. The reason why this assumption is unreasonable is a topic for a separate article.
Outro
I write a lot about blockchains and sharding, and we also have a video series where we talk to founders of scalable protocols, such as Cosmos and Solana, with tech deep dives. You can follow me on twitter here.