Стандартное отклонение и стандартная ошибка: две статистики с похожими названиями, но разными смыслами26.03.2024 10:45

Я читаю курс статистического мышления магистрам, и одна тема вызывает у них явные затруднения — чем стандартное отклонение отличается от стандартной ошибки и в каких случаях применять ту или иную статистику. Думаю, будет интересно поговорить об этом в блоге ЛАНИТ.

*Для иллюстрации я использовал Excel-файл. В нем вы найдете формулы, динамические данные на основе волатильных функций и статические данные, положенные в основу рисунков и расчетов для заметки. Корректно файл отображается в версии Excel 2016 или более поздней.

*Для иллюстрации я использовал Excel-файл. В нем вы найдете формулы, динамические данные на основе волатильных функций и статические данные, положенные в основу рисунков и расчетов для заметки. Корректно файл отображается в версии Excel 2016 или более поздней.

Случайные величины

Пусть — случайная нормально распределенная величина. Ее математическое ожидание в теории вероятностей обозначается M[X] или E[X] , а в статистике — . Сформируем две выборки по 100 значений. Для генерации выборок в Excel воспользуемся формулой =НОРМ.ОБР (СЛЧИС (); ; ). Зададим одинаковые матожидания μ_1 = μ_2 = 0 и разные среднеквадратичные отклонения: σ_1 = 1 и σ_2 = 2 .

Рис. 1. Нормально распределенные случайные величины. По оси абсцисс – номер элемента в выборке, по оси ординат – значение нормально распределенной случайной величины. Видно, что увеличение среднеквадратичного отклонения приводит к большему разбросу точек.

Рис. 1. Нормально распределенные случайные величины. По оси абсцисс — номер элемента в выборке, по оси ординат — значение нормально распределенной случайной величины. Видно, что увеличение среднеквадратичного отклонения приводит к большему разбросу точек.

Среднее арифметическое выборки

Несмотря на то, что мы задали для генерирующего процесса матожидание μ = 0 , среднее по выборке будет отличаться от этого значения. Среднее по выборке называют средним арифметическим $\bar{x}$ (или просто средним), и рассчитывают по формуле:

$(1)\bar x=\frac1n \displaystyle\sum_{i=1}^{n} x_i$

где x_i — отдельные значения случайной величины, — число значений случайной величины в выборке.

Для выборок на рис. 1 оказалось, что $\bar x_1 = 0,102$ , $\bar x_2 = -0,445$ .

Дисперсия и среднеквадратичное отклонение генеральной совокупности

Для измерения рассеяния (изменчивости) случайной величины относительно ее матожидания наиболее часто используют дисперсию, обозначаемую D[X] , Var[Х] или σ^2

$(2) σ^2=\frac1n\displaystyle\sum_{i=1}^{n} (x_i-μ)^2$

… и среднеквадратичное отклонение

$(3)σ=\sqrt {σ^2}=\sqrt{\frac{{\displaystyle\sum_{i=1}^{n} (x_i-μ)^2}}{n}}$

Стандартное отклонение выборки

Стандартное отклонение (Standard Deviation, SD) вычисляется по формуле:

$(4)s=\sqrt{\frac{{\displaystyle\sum_{i=1}^{n} (x_i-\bar{x})^2}}{n}}$

Вообще термины используются разными авторами немного по-разному. Мне нравится следующий подход. Генеральную совокупность описывают параметрами, обозначаемыми греческими буквами: математическое ожидание и среднеквадратичное отклонение . Выборки описывают статистиками, обозначаемыми латинскими буквами: среднее арифметическое $\bar{x}$ и стандартное отклонение .

В реальной жизни ни матожидание, ни среднеквадратичное отклонение σ генеральной совокупности неизвестны. Но, извлекая выборку, мы кое-что узнаем о матожидании и среднеквадратичном отклонении. Говорят, что среднее $\bar{x}$ является оценкой матожидания, а стандартное отклонение — оценкой среднеквадратичного отклонения σ.

При генерации случайной величины мы задали σ_1 = 1 и σ_2= 2 . Для выборок на рис. 1 получили s_1 = 0,985 , s_2 = 1,824 .

Чем меньше , тем кучнее значения располагаются вокруг среднего. Итак,

стандартное отклонение — мера разброса данных в выборке

Стандартное отклонение средних значений выборок

Сосредоточимся теперь на процессе генерации случайных чисел с μ = 0 и σ = 1 . Извлечем не одну выборку, а несколько. Хотя аргументы и генератора случайных чисел постоянны, случайный процесс будет приводить к разным значениям $\bar{x}$ для отдельных выборок:

Рис. 2. Средние значения для 15 выборок размером

Рис. 2. Средние значения для 15 выборок размером n = 100

Если возьмем не 15, а 1000 выборок, то сможем построить довольно гладкое распределение средних значений $\bar{x}$ :

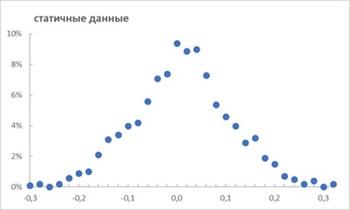
Рис. 3. Распределение средних значений для 1000 выборок размером . По оси абсцисс диапазоны средних значений выборок, по оси ординат доля таких выборок

Рис. 3. Распределение средних значений $\bar{x}$ для 1000 выборок размером n=100

. По оси абсцисс диапазоны средних значений выборок, по оси ординат доля таких выборок

Совокупность средних $\bar{x}_i$ можно рассматривать как случайную величину $\bar{X}$ . Для ее распределения (рис. 3) также можно подсчитать стандартное отклонение по формуле (4): $s_{\bar{X}} = 0,1$ . Нижний индекс $\bar{X}$ указывает, что стандартное отклонение относится к средним значениям $\bar{x}_i$ . Обратите внимание, что стандартное отклонение одной выборки (рис. 1а) равнялось s_1 = 0,985 . Стандартное отклонение каждой выборки задается генерирующим процессом, в котором среднеквадратичное отклонение генеральной совокупности σ_1 = 1 . Для средних значений выборок размером n = 100 стандартное отклонение $s_\bar{X}$ приблизительно в 10 раз меньше, чем для отдельных значений в выборке s_1 .

Подсчитаем стандартное отклонение для 100 выборок других размеров n = 3, 5, 10, 20 . Оказывается, что стандартное отклонение средних значений зависит от размера выборки:

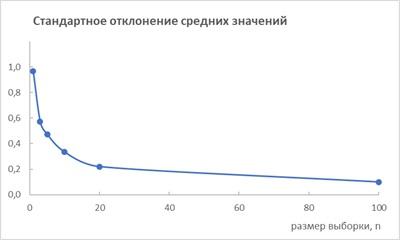
Рис. 4. Зависимость стандартного отклонения средних значений от размера выборок

Рис. 4. Зависимость стандартного отклонения средних значений от размера выборок

Выведем формулу этой зависимости.

Формула стандартной ошибки

Для начала покажем, что постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

По определению дисперсия Var случайной величины равна

(5)Var(X)=E[(X-E[X])^2]

где E[X] — математическое ожидание случайной величины X, E[(X-E[X])^2] — математическое ожидание квадрата разности самой случайной величины и ее матожидания.

Рассмотрим теперь случайную величину Y = cX , где — константа. Найдем дисперсию

(6)Var(Y)=E[(Y-E[Y])^2]=E[(cX-E[cX])^2]=E[c^2(X-E[X])^2]=c^2E[(X-E[X])^2]=c^2Var(X)

С другой стороны, среднее арифметическое по выборке:

$(7)\bar{x}={\frac{x_1+x_2+…+x_n}{n}}$

Дисперсия выборки:

$(8)Var(\bar{x})=Var({\frac{x_1+x_2+…+x_n}{n}})=\frac{1}{n^2}Var(x_1+x_2+…+x_n)$

Здесь мы воспользовались только что выведенным свойством (6), используя с = 1/n .

Теперь учтем, что дисперсия суммы независимых случайных величин равняется сумме их дисперсий:

$(9)Var(\bar{x})=\frac{1}{n^2}Var(x_1+x_2+…+x_n)={\frac{Var(x_1)+Var(x_2)+…+Var(x_n)}{n^2}}$

Примем во внимание, что все случайные величины x_i одинаково распределены:

$(10)Var(\bar{x})={\frac{Var(x_1)+Var(x_2)+…+Var(x_n)}{n^2}}={\frac{nVar(x)}{n^2}}={\frac{Var(x)}{n}}$

Извлекая корень и переходя от параметра генеральной совокупности к статистике выборки, можем записать стандартное отклонение случайной величины $\bar{X}$ :

$(11)s_{\bar{X}}={\frac{s_1}{\sqrt{n}}}$

Мы получили зависимость стандартного отклонения средних значений выборок $s_{\bar{X}}$ от стандартного отклонения единичных значений s_1 и размера выборки . Если в (11) подставить (4), получим:

$(12)s_{\bar{X}}=\sqrt{\frac{{\displaystyle\sum_{i=1}^{n} (x_i-\bar{x})^2}}{n^2}}$

Величину $s_{\bar{X}}$ называют стандартной ошибкой или стандартной ошибкой среднего. $s_{\bar{X}}$ позволяет по одной выборке оценить в каком диапазоне от среднего по выборке $\bar{x}$ находится матожидание генеральной совокупности . Например, в диапазон ${\bar{x}} ± 2s_{\bar{X}}$ матожидание генеральной совокупности попадет с вероятностью 95%.

Если стандартное отклонение — это показатель изменчивости элементов в выборке, то стандартная ошибка — аналогичный показатель (вычисляемый по той же формуле) изменчивости средних значений выборок.

Итак,

стандартная ошибка — мера оценки математического ожидания генеральной совокупности μ на основании выборочного среднего $\bar{x}$ .

Обратите внимание, что с увеличением размера выборки стандартная ошибка будет уменьшаться. В пределе при n → ∞ , x̅ → μ и $s_\bar{X} → 0$ .

Смещенные и несмещенные оценки

Оценку параметра генеральной совокупности в общем случае можно представить уравнением:

(13) Оценка = Оцениваемый параметр генеральной совокупности + Смещение + Шум

Оказывается, что среднее арифметическое является несмещенной оценкой матожидания:

$(14) \bar{x} = μ + Шум$

Чтобы проиллюстрировать этот вывод, я случайным образом задал 10 000 чисел в диапазоне от 0 до 100. А затем создал 100 выборок по 100 последовательных значений: от 1 до 100, от 101 до 200 и т.д. На график в виде пунктирной линии нанес среднее значение для всех 10 000 случайных чисел, а также в виде точек — скользящее среднее для последовательности выборок. Например, первая точка — среднее арифметическое для первой выборки: 1…100, вторая точка — среднее статистик двух выборок: 1…100 и 101…200 и т.д.

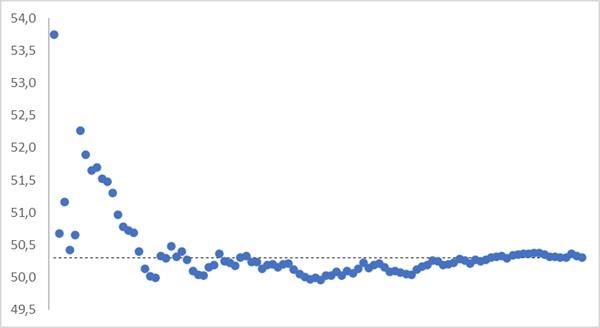
Рис. 5. Среднее арифметическое, как несмещенная оценка матожидания. Видно, что среднее выборок стремится к среднему по всей совокупности.

Представляется парадоксальным, но стандартное отклонение оказалось смещенной оценкой среднеквадратичного отклонения:

(15) s = σ + Смещение + Шум Рис. 6. Стандартное отклонение, как смещенная оценка среднеквадратичного отклонения

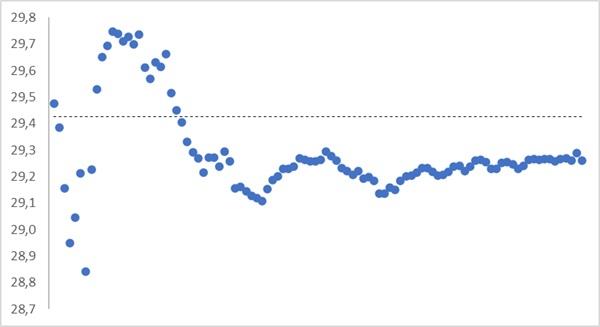
Рис. 6. Стандартное отклонение, как смещенная оценка среднеквадратичного отклонения

Выборочная оценка среднеквадратичного отклонения, названная нами стандартным отклонением, и введенная формулой (4) дает систематическую ошибку!

Поправка Бесселя

Чтобы разобраться с источником систематической ошибки, еще раз приведем формулы среднеквадратичного и стандартного отклонений.

$(3)σ=\sqrt{\frac{{\displaystyle\sum_{i=1}^{n} (x_i-μ)^2}}{n}}$ $(4)s=\sqrt{\frac{{\displaystyle\sum_{i=1}^{n} (x_i-\bar{x})^2}}{n}}$

… и вернемся к примеру на рис. 1а.

Мы знаем (сами задали в Excel), что матожидание генеральной совокупности μ = 0 . Но среднее арифметическое выборки $\bar{x}=0,102$ . И это наша лучшая оценка матожидания. Правильная (несмещенная) оценка среднеквадратичного отклонения генеральной совокупности σ должна была бы основываться на отклонениях от μ = 0 по формуле (3). Но если мы не знаем истинное значение , то вычисляем стандартное отклонение от $\bar{x}$ по формуле (4).

Заметим, что в формуле (3) можно представить, как $\bar{x}– с$ , где – константа (смещение), показывающая насколько выборочное среднее отличается от матожидания генеральной совокупности. Тогда x_i – μ можно заменить на $x_i – \bar{x} + с$ . Обозначим разность $x_i – \bar{x}$ одним символом a_i . В формуле (4) мы ищем сумму a_i^2 , а в формуле (3) — сумму (a_i + с)^2 . Но

(16) (a_i + c)^2 = a_i^2 + 2a_ic + c^2

По определению сумма вторых слагаемых по выборке Σ2a_ic равна нулю — отклонения от среднего в разные стороны компенсируют друг друга. На то оно и среднее. Сумма a_i^2 представляет собой сумму квадратов расстояния от значений выборки до среднего выборочного значения. c^2 — сумма квадратов расстояний между средним арифметическим по выборке и матожиданием генеральной совокупности.

Поскольку c^2 положительна (за исключением случая, когда $\bar{x} = μ$ ) сумма квадратов расстояния от значений выборки до матожидания генеральной совокупности всегда будет больше, чем сумма квадратов расстояния до выборочного среднего.

Вот почему дает систематическую ошибку (в сторону уменьшения) по сравнению с .

В смещенной оценке , используя выборочное среднее вместо матожидания, мы недооцениваем каждое $x_i-\bar{x}$ на $\bar{x} – μ$ .

Чтобы найти расхождение между смещенной оценкой и параметром генеральной совокупности σ, нужно найти матожидание $E(\bar{x} – μ)$ . В разделе Формула стандартной ошибки мы показали, что это матожидание равно дисперсии выборочного среднего σ/n. Таким образом, смещенная оценка занижает на σ/n :

(17) смещенная оценка $=(1-\frac1n) *$ несмещенная оценка $=\frac {n-1}{n}*$ несмещенная оценка

Поправкой Бесселя называют коэффициент $(18)\sqrt{\frac{n}{n-1}}$ , на который следует умножить стандартное отклонение, чтобы смещенную оценку сделать несмещенной:

$(19)s_{несмещ}=\sqrt{\frac{{\displaystyle\sum_{i=1}^{n} (x_i-\bar{x})^2}}{n}} ∙ \sqrt{\frac{n}{n-1}} =\sqrt{\frac{{\displaystyle\sum_{i=1}^{n} (x_i-\bar{x})^2}}{n-1}}$

Проверим поведение $s_{несмещ}$ на модели:

Рис. 7. Стандартное отклонение, как несмещенная оценка среднеквадратичного отклонения

Поправку Бесселя следует ввести и в формулу (12) для расчета стандартной ошибки среднего. Получим:

$(20)s_\bar{X}=\sqrt{\frac{{\displaystyle\sum_{i=1}^{n} (x_i-\bar{x})^2}}{n^2}} * \sqrt{\frac{n}{n-1}} =\sqrt{\frac{{\displaystyle\sum_{i=1}^{n} (x_i-\bar{x})^2}}{n(n-1)}}$

Допущения

При выводе формул стандартного отклонения и стандартной ошибки явно или неявно мы использовали следующие допущения:

данные в выборке подчиняются нормальному распределению;
выборка является репрезентативной для генеральной совокупности;
наблюдения в выборке независимы друг от друга; для временных рядов допущение о независимости как правило нарушено;
измерения проводятся на интервальной или относительной шкале; использование категориальных данных может быть некорректным;
оценки чувствительны к выбросам.

Посмотрим, что происходит, когда одно или несколько допущений нарушены.

Распределения с жирными хвостами

Нормальное распределение обладает тонким хвостом. Это означает, что поведение нормально распределенной случайной величины определяется центральной частью распределения. Хвостовые значения встречаются очень редко. Центральная предельная теорема дает быструю сходимость, и мы наблюдаем характерное поведение, как на рис. 5.

На мой запрос ChatGPT указал три области, где данные хорошо описываются нормальным распределением: рост людей, ошибки измерения (длины или массы среди однородной группы объектов), интеллектуальные способности (тесты IQ разработаны с учетом нормального распределения, и средний уровень интеллекта обычно приходится на центральную часть распределения).

Нормальное распределение настолько растиражировано, что мы используем его даже тогда, когда этого делать не следует — при работе с финансовыми инструментами, экономическими и социальными явлениями. Типичный пример — средний доход посетителей бара, который взлетит до миллиарда, если туда случайной зайдет Билл Гейтс.

Посмотрим, как сходится к среднему случайная величина, заданная стандартным распределением Коши:

$(21) f(x)=\frac{1}{π(1+x^2)}$

Для моделирования в Excel я воспользовался тем фактом, что t-распределение Стьюдента с числом степеней свободы df = 1 эквивалентно стандартному распределению Коши. А для t-Стьюдента в Excel есть формулы прямого и обратного распределений.

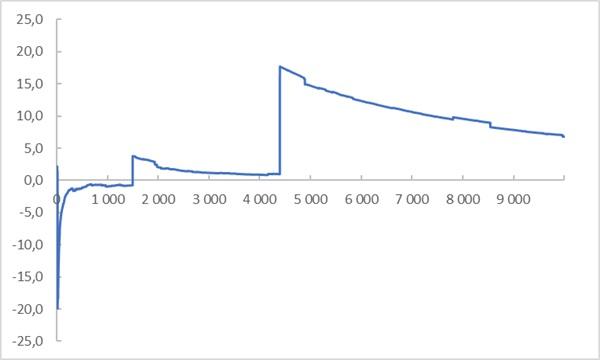
Рис. 8. Сходимость распределения Коши вроде бы есть… но только до очередного выброса

Рис. 8. Сходимость распределения Коши вроде бы есть…, но только до очередного выброса

Если мы посмотрим на допущения, сформулированные выше, то увидим, что данные, распределенные по Коши, нарушают почти все. (1) Никакая выборка не является репрезентативной. Хвостовые значения всё еще относительно редки (правда, не настолько, как при нормальном распределении), но именно они определяют среднее по выборке. (2) Наличие или отсутствие выброса в выборке сильнее влияет на среднее арифметическое, чем центральная тенденция.

Вслед за средним арифметическим, и стандартное отклонение, и стандартная ошибка, полученные на основе выборки, мало что говорят о генеральной совокупности.

В качестве примера я привел экстремально жирнохвостое распределение Коши, но и многие иные распределения, например, степенные, ведут себя лишь немногим более предсказуемо. Эта тема подробно раскрыта в новой книге Нассима Талеба (см. ссылку ниже).

Области использования

Вот несколько областей использования стандартного отклонения:

Оценка разброса данных (изменчивости) относительно среднего значения. Чем больше стандартное отклонение, тем больше разброс.
Оценка качества как индикатор изменчивости процесса производства или управления. Меньшее стандартное отклонение говорит о более стабильном процессе. Стандартное отклонение может использоваться для построения границ контрольных карт Шухарта.

Области использования стандартной ошибки среднего (Standard Error of the Mean, SEM):

Доверительные интервалы для среднего значения. Например, если вы провели опрос с небольшой выборкой и вычислили среднее и SEM, то можете построить доверительный интервал, указывающий, где находится истинное среднее в генеральной совокупности.
При сравнении средних значений из разных выборок SEM используется для определения статистической значимости различий между выборками. Если разница средних значений превышает несколько SEM, это может свидетельствовать о статистически значимом различии.
SEM указывает, насколько точно среднее выборки оценивает истинное среднее в генеральной совокупности. Большая SEM указывает на большую неопределенность в оценке.

С осторожностью и оговорками стандартное отклонение и стандартную ошибку следует применять для оценки рисков в финансовой сфере. Формулы SD и SEM основаны на нескольких статистических предположениях. Важно понимать эти допущения при использовании и интерпретации результатов.

Литература

Владимир Гмурман. Теория вероятностей и математическая статистика
Поправка Бесселя, Bessel’s correction
Нассим Николас Талеб. Статистические последствия жирных хвостов.