Способы хранения графа в памяти компьютера

В предыдущей статье мы познакомились с терминами и определениями теории графов. В этой же статье обсудим различные способы представления графа в памяти компьютера для его обработки. Покажем, какие структуры данных можно использовать, а также проговорим преимущества и недостатки каждого способа.
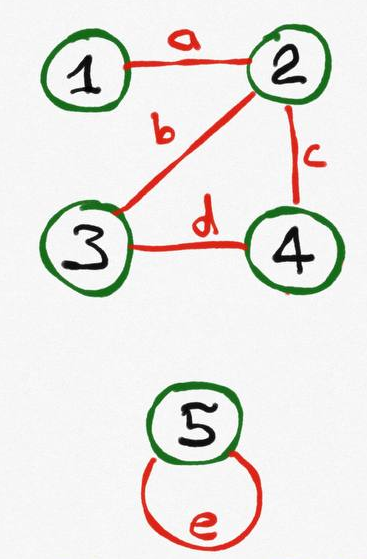
Допустим, у нас есть неориентированный граф G из V = 5 вершин и E = 6 рёбер. Вершины пронумерованы от 1 до 5, рёбра для удобства также пронумеруем буквами a, b, c, d, e. Одна вершина с петлёй, изолирована от других.
Перечисление множеств
По определению, граф — это топологическая модель, которая состоит из множества вершин и множества рёбер, их соединяющих. Значит, самый «простой» способ представить граф — определить оба этих множества.
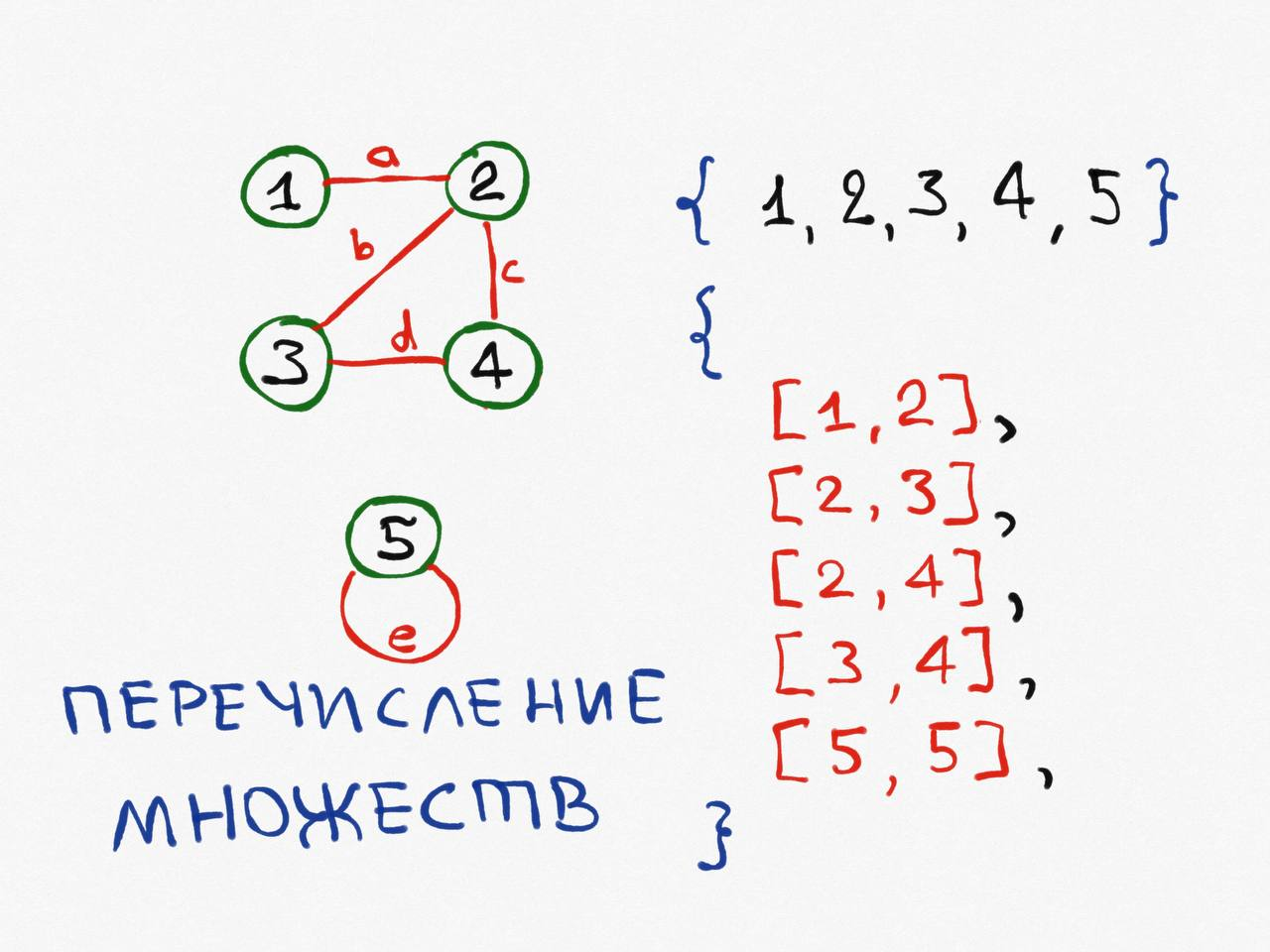
Лично мне ни разу не доводилось видеть алгоритм обработки графа, который бы использовал такой способ хранения вершин и рёбер.
Недостаток такого подхода: использование достаточно тяжеловесной структуры — хэш таблицы — для хранения множества, когда проще и быстрее работать с обычными массивами или списками, к тому же, во множестве нет возможности получить перечисление вершин в порядке их добавления (особенность хэш-таблицы).
Кстати, сами вершины обычно вообще отдельно не хранятся, а указывается только их количество V, они автоматически принимают номера от 0 до V-1. Для хранения цвета / веса или других характеристик вершин можно использовать параллельные массивы для каждого критерия.
Матрица смежности
Это самый популярный и расточительный способ представления графа в памяти. Его уместно использовать, если количество рёбер велико, порядка V^2.
Для хранения рёбер используется двумерная матрица размерности [V, V], каждый [a, b] элемент которой равен 1, если вершины a и b являются смежными и 0 в противном случае.
В случае неориентированного графа матрица является симметричной относительно главной диагонали, а сумма каждой строчки и каждого столбца равна степени вершины. В связи с этим, при записи рёбер-петель в матрицу необходимо записывать число 2.
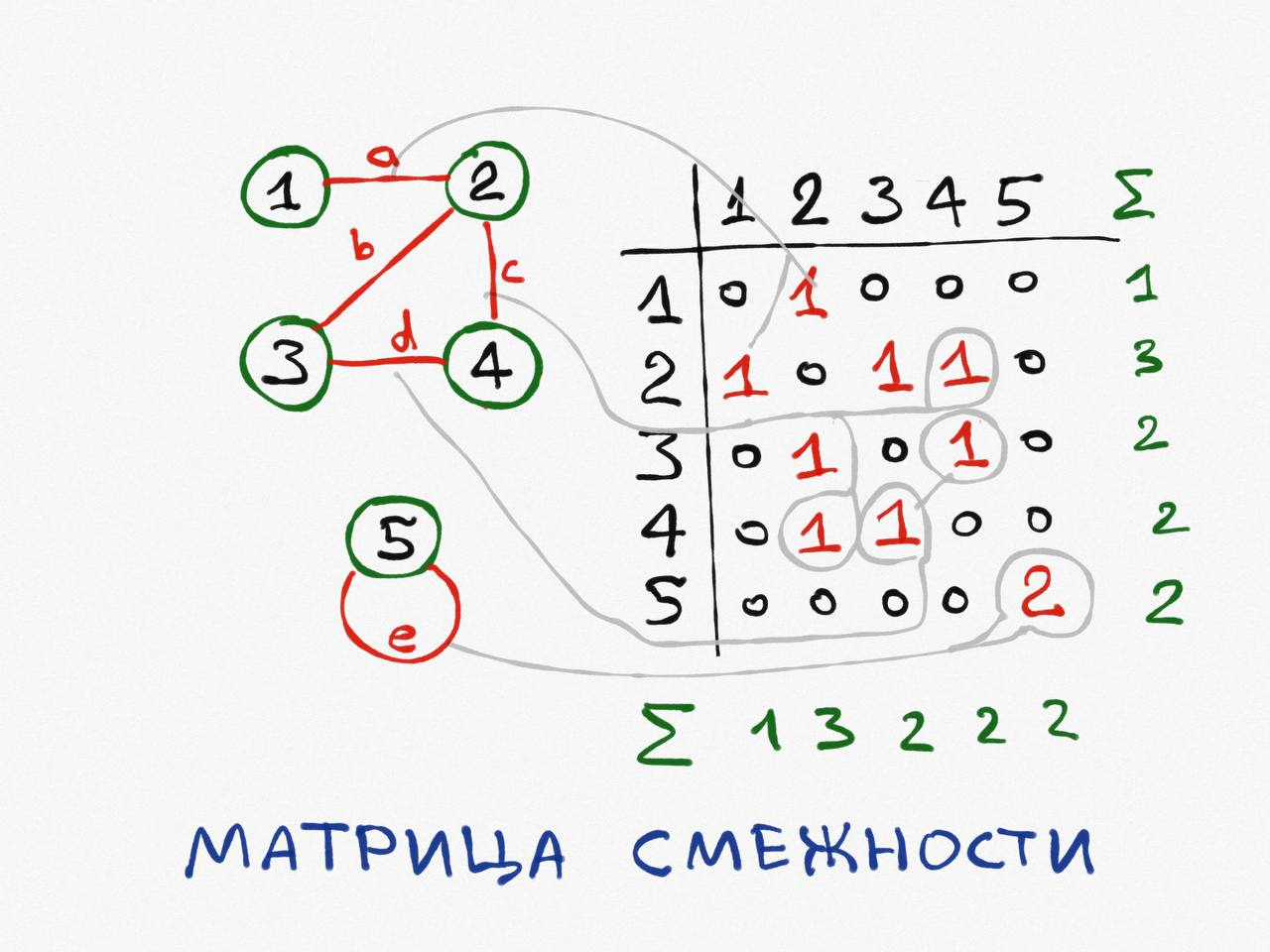
Сложность по памяти: O (V^2).
Сложность перечисления всех рёбер: O (V^2).
Сложность перечисления всех вершин, смежных с а: O (V).
Сложность проверки смежности вершин a и b: О (1).
Матрица инцидентности
Это самый расточительный способ хранения графа, его уместно использовать, если количество рёбер невелико.
Для хранения используется двумерная матрица размера [V, E], в каждом столбце которой записано одно ребро таким образом: напротив вершин, инцидентных этому ребру, записаны 1, в остальных случаях 0.
Таким образом, сумма чисел в каждом столбце равна 2, а сумма чисел в строчке a равна степени вершины а.
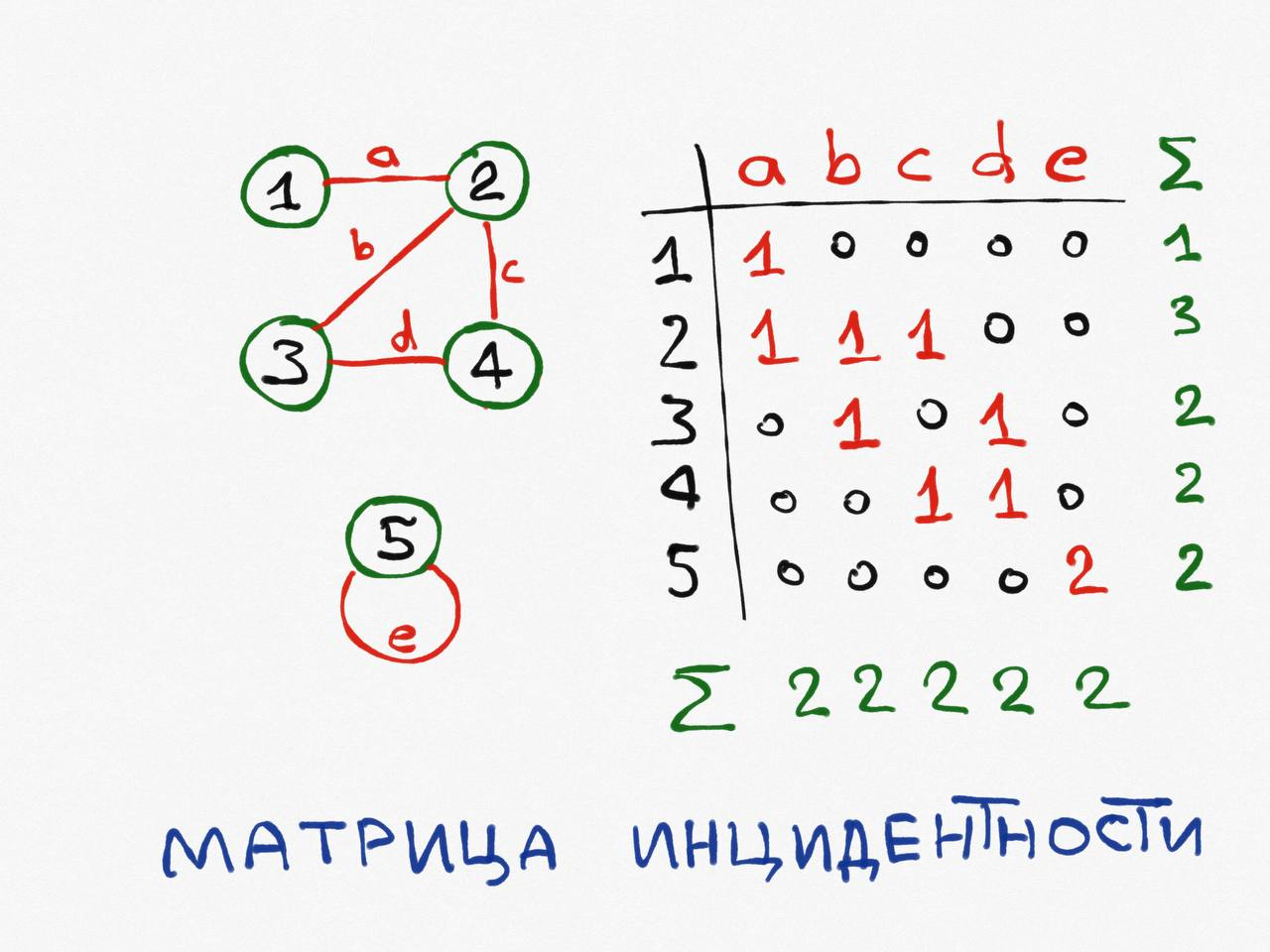
Сложность по памяти: O (V x E).
Сложность перечисления всех рёбер: O (V x E) — хоть каждое ребро и хранится в отдельном столбце, но для получения информации об инцидентных ему вершинах нужно перебрать все числа в столбце.
Сложность перечисления всех вершин, смежных с а: O (V x E).
Сложность проверки смежности вершин a и b: O (E) — достаточно пройтись по строчкам a и b в поисках двух единиц.
Перечень рёбер
Если из матрицы инцидентности убрать все нули, в каждом столбце останется только два числа для каждого ребра — номера инцидентных ему вершин. То есть, для перечисления рёбер достаточно составить список из пар чисел, это очень экономный способ: каждое ребро хранится один раз, когда во всех других вариантах каждое ребро, как правило, записывается дважды.
Недостаток — при поиске вершин в списке рёбер нужно выполнять по две проверки — сравнивать и первую вершину, и вторую.

Сложность по памяти: O (E).
Сложность перечисления всех рёбер: O (E).
Сложность перечисления всех вершин, смежных с а: O (E).
Сложность проверки смежности вершин a и b: О (E).
Список рёбер можно сгруппировать по вершинам, что позволит ускорить поиск смежных вершин. У нас получится ещё три очередных способа, которые очень похожи друг на друга, отличаются лишь способом записи векторов.
Векторы смежности
Для записи вектора смежности используется двумерная матрица размером [V, S], где S — максимальная степень вершины в графе.
В каждой строчке a записаны номера вершин, смежных с а, после чего записаны нули (несуществующие номера вершин).

Сложность по памяти: O (V x S).
Сложность перечисления всех рёбер: O (V x E)
Сложность перечисления всех вершин, смежных с а: O (Sa) (Sa = степень вершины а)
Сложность проверки смежности вершин a и b: О (Sa) = O (Sb)
Массивы смежности
Для экономии памяти, используется ступенчатый массив, длина каждой строки равна степени данной вершины.

Сложность по памяти: O (сумма степеней всех вершин).
Списки смежности
Здесь используется односвязный список для перечисления всех смежных вершин.
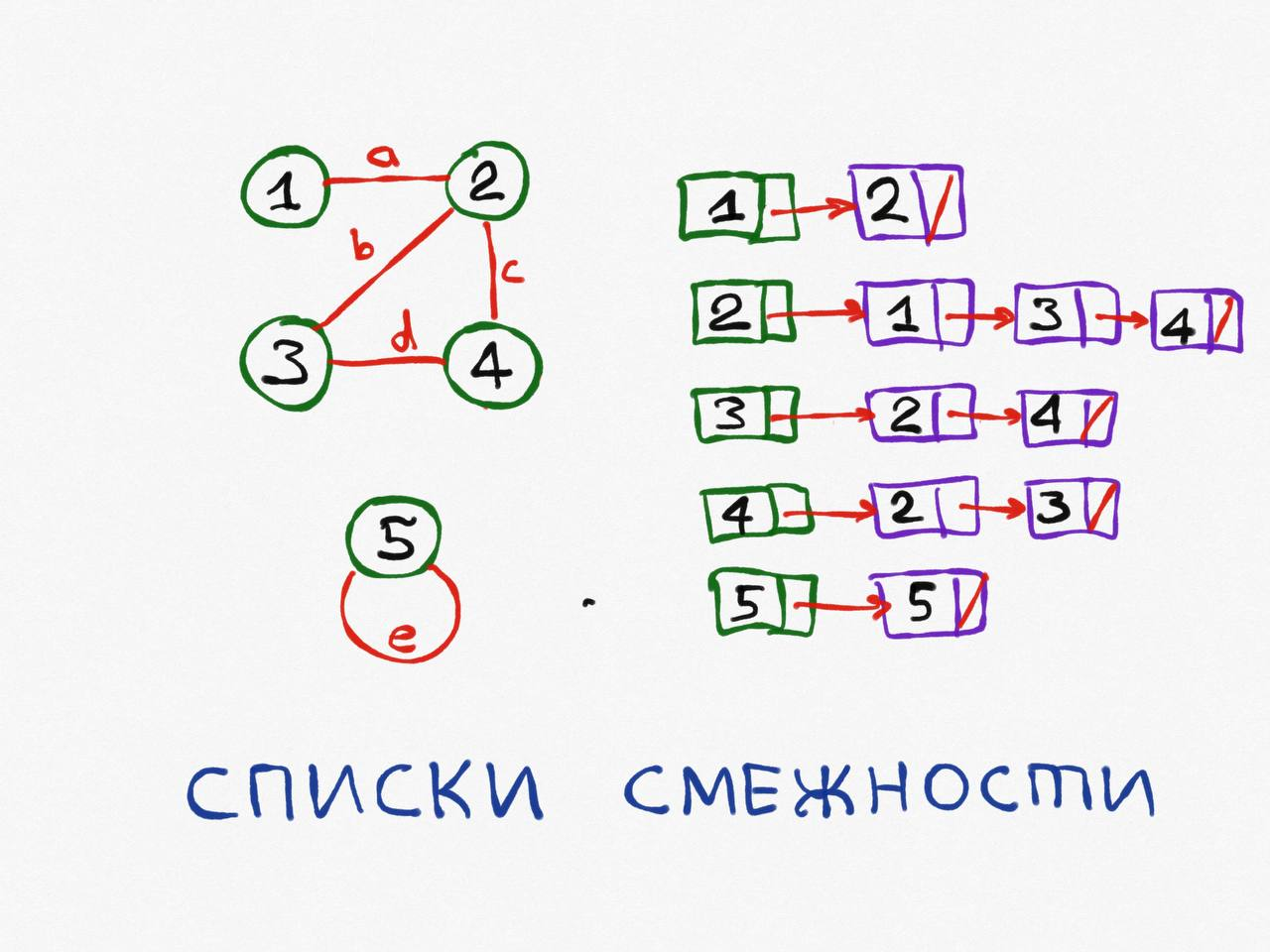
Сложность по памяти: O (V + сумма степеней всех вершин).
Структура с оглавлением
Один из самых экономных способов представления графа в памяти. Фактически, мы записываем все массивы смежности в одну строчку, в один линейный массив, и создаём массив-оглавление, с указателями на начало списка для каждой вершины.
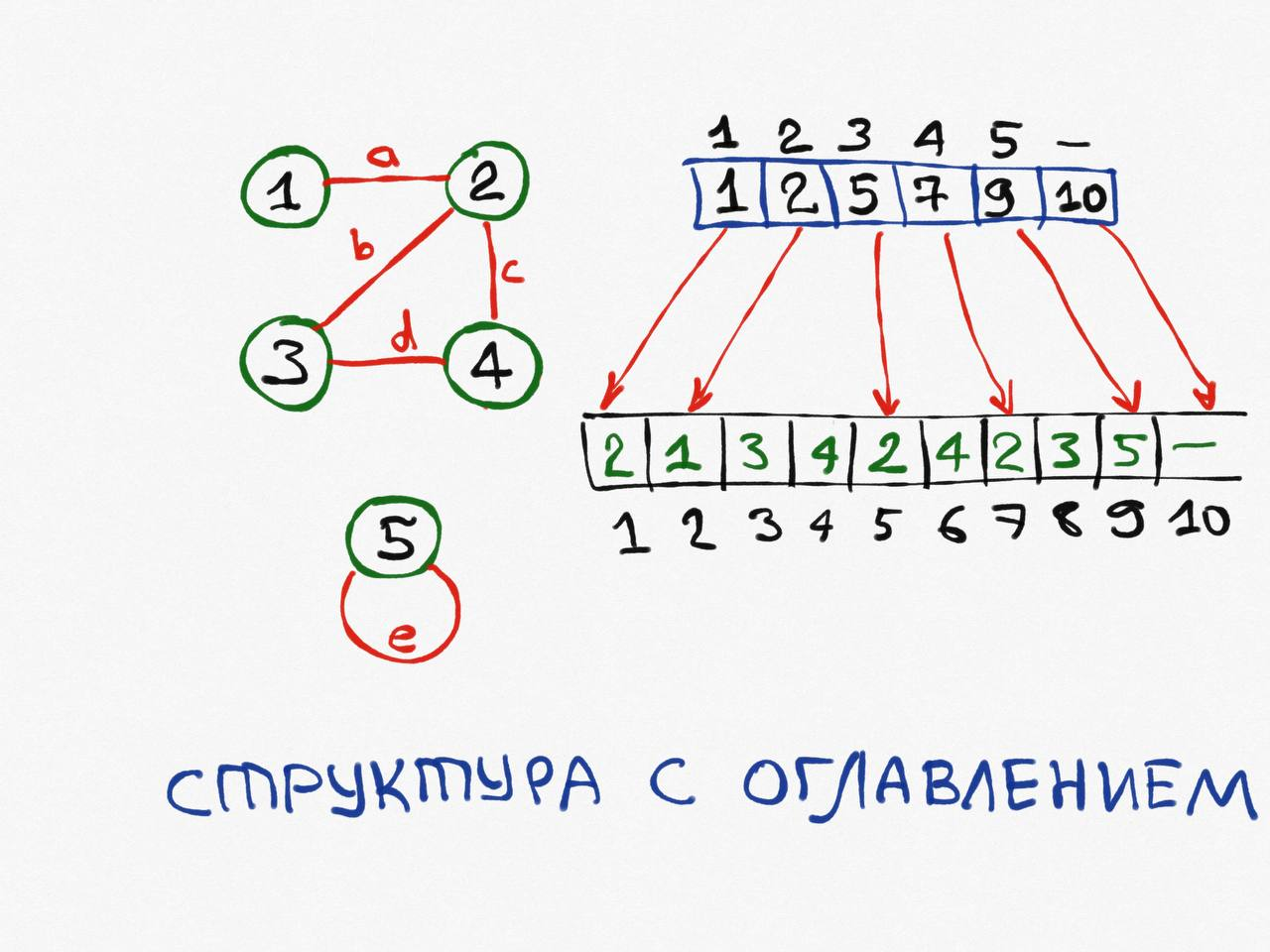
Сложность по памяти: O (V + сумма степеней всех вершин).
Список вершин и список рёбер
Самый экстравагантный способ хранения графа.
Вершины записываются в односвязных список, от каждой вершины есть указатель на список всех рёбер, инцидентных данной вершины. Каждое ребро, в свою очередь, имеет указатель на вторую инцидентную ей вершину и на следующее ребро.
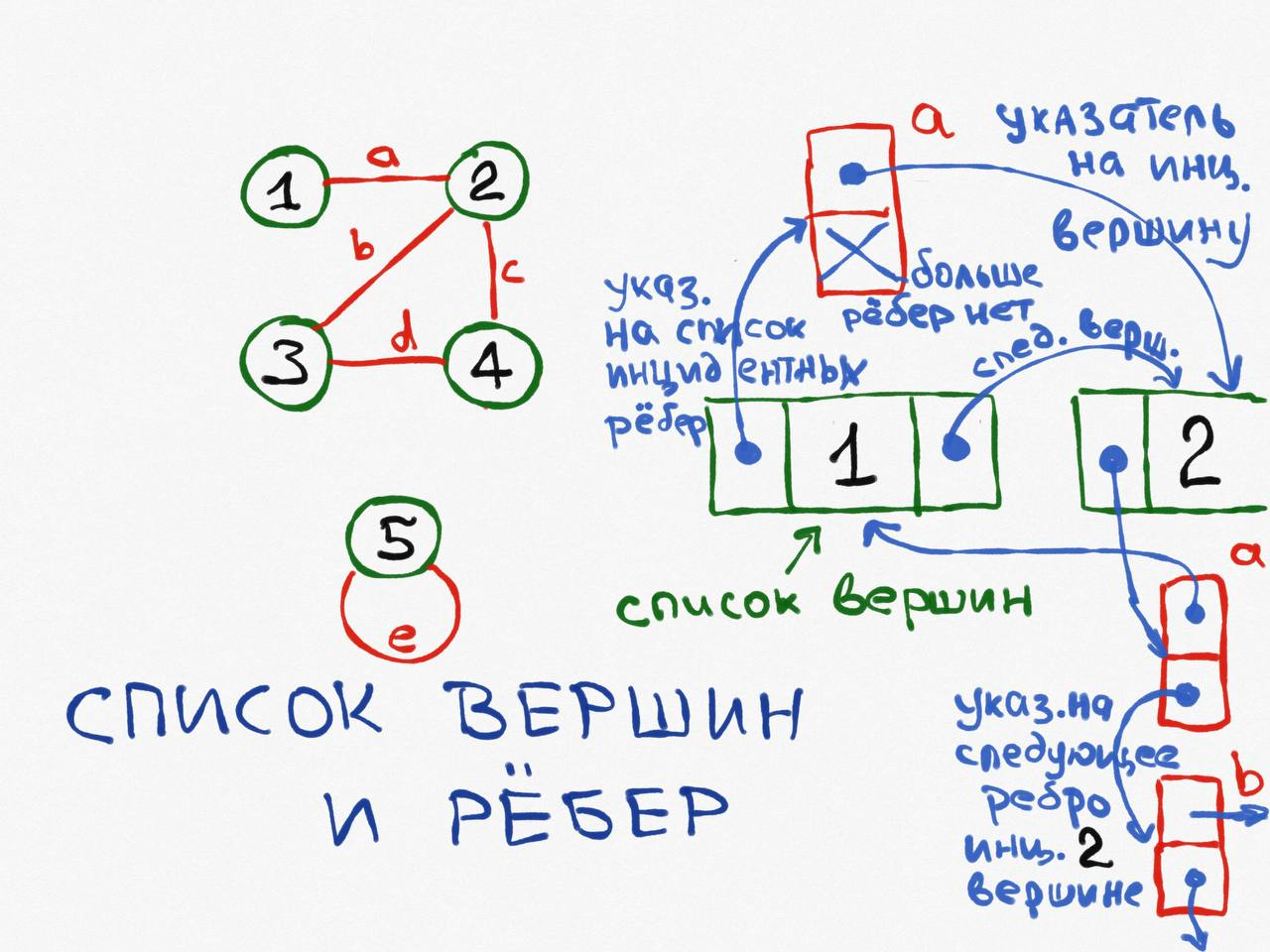
Получается весьма разветвлённый граф для представления графа.
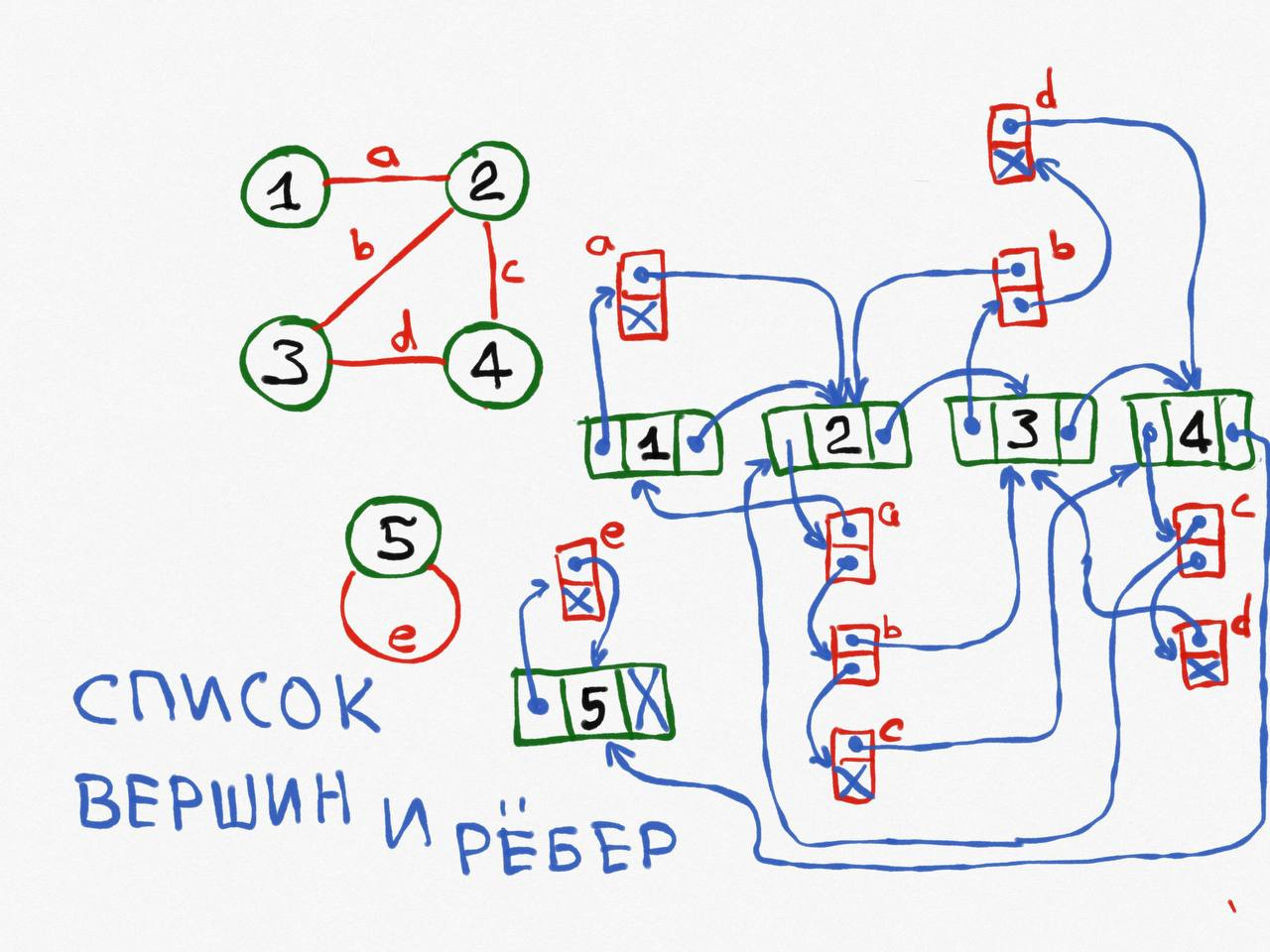
Сложность по памяти: O (V + сумма степеней всех вершин).
Сложность перечисления всех рёбер: O (V x E)
Сложность перечисления всех вершин, смежных с а: O (Sa) (Sa = степень вершины а)
Сложность проверки смежности вершин a и b: О (Sa) = O (Sb)
Теперь, когда мы знаем способы представления графа в памяти компьютера, можем выбирать наиболее приемлемые варианты для каждой конкретной задачи.
На курсе «Алгоритмы и структуры данных» мы рассматриваем следующие алгоритмы в модуле «Теория графов»: поиск вширь и вглубь, топологическая сортировка (Кана, Таряна, Демукрона), поиск компонент сильной связности (Косарайю), поиск минимального скелета (Прима, Краскала, Борувки), поиск кратчайшего пути (Флойда-Уоршалла, Баллмана-Форда, Дейкстры), алгоритм Джонсона для поиск кратчайшего пути в орграфе с отрицательными дугами (см. мою статью), решение задачи коммивояжера (ближайшего соседа, кратчайшего ребра, ближайшего посредника) и вишенка на торте — алгоритм А* звезда поиска кратчайшего пути с эвристической функцией.
Также хочу пригласить всех желающих на бесплатный демоурок по теме «Дерево отрезков — быстро и просто». Зарегистрироваться на урок.
