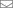Случайный трамвай посреди незнакомого города08.09.2020 15:17

Есть одна довольно любопытная задачка, она уже давно вошла в математический фольклор, а так же стала излюбленным испытанием на собеседованиях. Ее условия просты, а решение, кажется напрашивается само собой, однако не будем торопиться с выводами. Берите карандаш, чистый лист бумаги, усаживайтесь поудобней и давайте во всем разбираться.

В чем же, собственно, задача

Итак представьте, что Вы приехали в абсолютно незнакомый город и первый трамвай, который вам там повстречался, следовал под номером 17. Как оценить, сколько всего в этом городе трамвайных маршрутов?

Для простоты считайте, что трамвайные маршруты в городе пронумерованы без пропусков числами от 1 до N и изначально каждое из этих чисел с равными шансами могло оказаться номером трамвая, которого вы бы увидели первым.

Впервые задачу о «Случайном трамвае» я услышал от Николая Николаевича Васильева, моего знакомого питерского математика. Тогда же он поделился со мной наблюдением, что среди тех, кому он рассказывал эту задачу, а затем просил дать ответ не задумываясь, большинство людей назвало число 34, то есть »x2» от 17. На моем опыте самым экстравагантным был ответ моего товарища с «мехмата»: 17. Только через неделю я догадался, что им двигал спавший где-то на подкорке его мозга принцип максимизации правдоподобия. Хорошо, но 17 и 34, другими словами »x1» и »x2» — это наивные и необдуманные ответы, а какой тогда правильный ответ, и вообще, существует ли он у этой задачи.

Подводные камни и область фантазии

Почему же стоит сомневаться насчет существования универсально-правильного ответа? К такой мысли легко прийти, если рассмотреть несколько простых, пускай и вымышленных вселенных. К примеру представьте, что на Земле в каждом городе ровно по 30 трамвайных маршрутов. Будет ли в этой вселенной »30» — единственно верным ответом? Теперь представьте, что в другой вселенной на Земле 1000 городов, причем в 999 из них действует по 30 трамвайных маршрутов, а в оставшемся одном — их ровно 17. Какой на сей раз ответ будет правильным и как на него повлияет то обстоятельство, что городов с 30-ю маршрутами очень много, а с 17-ю — всего один? Сразу скажу, что пользоваться вероятностными соображениями здесь очень трудно, ведь человек, которого просят оценить число маршрутов, не знает, был ли город, в котором он сейчас гостит, выбран на карте случайно, или в этом выборе кроется некая причина и присутствует чей-то расчет.

Принцип крайнего математического пессимизма

Несмотря на заявленные трудности, в математике имеется принцип, при помощи которого для нашей задачи можно дать ответ, остающийся осмысленным даже в самых причудливых мирах.
Когда дело касается игр, этот принцип называют максимизацией гарантированного выигрыша,
и чтобы понять в чем кроется его суть, давайте рассмотрим один простой пример.

Представьте себе игру: скрытно от вас в один из своих кулаков я прячу маленький предмет, пусть это будет сухая горошина, затем вытягиваю руки вперед и прошу вас угадать, в какой из них эта горошина находится. Пусть у нас есть время, чтобы сыграть очень долгую партию игр, причем изначально вам не известно, пытаюсь ли я вас в ней обыграть, стараюсь намеренно поддаться, или сохраняю безразличие к вашему успеху. Предположим, что перед вами стоит цель: выиграть как можно больше игр. Какой стратегии вам в таком случае стоило бы придерживаться?

Для начала давайте попробуем проанализировать, преимущества и недостатки следующих четырех простеньких стратегий:

Всегда выбирать правую руку.
Начать с правой, а затем выбирать ту руку, в которой горошина была найдена в последний раз.
В каждой игре перед тем, как сделать выбор, бросить на стол игральную кость. Если выпало »1» или »2», то выбрать правую руку, на »3»,»4»,»5» и »6» — левую.
Как и в предыдущей стратегии, в каждой игре бросить кость. В тех случаях, когда выпавшая грань оказалась «четной», выбрать правую, а когда «нечетной» — левую.

Если вы решите воспользоваться стратегией 1) и при этом я буду прятать горошину всегда в правой руке, то все игры завершатся в вашу пользу. Можно сказать, что сценарий развития партии, при котором я прячу горошину исключительно в правую руку, является для 1)наилучшим. Однако в своем наихудшем сценарии, сценарии, где я прячу горошину исключительно в левой руке, стратегия 1) не позволит вам выиграть ни одной игры, какой бы долгой не была наша партия.

Легко догадаться, что стратегия 2) страдает тем же «пороком», а именно в наихудшем для нее сценарии, когда я начинаю с левой руки и затем в каждой из следующих игр чередую руки, она не позволит вам выиграть ни разу, как бы долго не длилась наша партия.

Займемся теперь стратегией, которая идет в нашем списке третьей. Если вы ею воспользуетесь, то ваши шансы на победу в каждой игре, где горошина будет спрятана в правую руку, составят ⅓, а в играх, в которых горошина будет находится в левой, — 2/3. Понятное дело, что наихудший сценарий для 3) — это, когда я имею привычку прятать горошину исключительно в правой руке. Однако даже в этом случае в любой достаточно длинной партии игр, примерно треть из них завершится вашей победой. Теоретически вам конечно может и не повезти, и правильную руку вы не отгадаете ни разу, но практически, скажем в партии из 1000 игр, почти не вероятно, чтобы количество ваших побед было меньше, чем $333-4\sqrt{1000\ \cdot1/3\cdot2/3}\$ , то есть меньше чем $333 - 60$ , а в партии из миллиона игр возможный процент отличий будет еще меньше. По сути, выбрав стратегию 3), вы тем самым гарантируете себе, что примерно треть от игр партии останутся за вами.

Если вы воспользовались четвертой в списке стратегией, то наша игра приобретает интересную особенность: по сути для вас перестает быть важным, на сей раз я спрятал горошину в правой руке или положил ее в левую, потому как в обеих ситуациях ваши шансы на победу будут одинаковы и составят ровно 50%. Можно даже сказать, любая намеченная мною очередность рук, где я собираюсь прятать горошину, для вас будет является одновременно и наилучшим и наихудшим сценарием развития партии. Получается, что при любых раскладах в достаточно долгой партии игр примерно половина из них должны закончиться вашей победой. В этом смысле стратегия 4) дает вам самые большие гарантии, по сравнению со всеми остальными стратегиями, которые мы уже успели здесь рассмотреть.

Принцип максимизации гарантированного выигрыша предписывает вам перебрать все возможные стратегии игры, для каждой из них вычислить величину выигрыша в наихудшем для нее сценарии и объявить оптимальной ту стратегию, для которой величина этого выигрыша окажется наибольшей. Можно показать, что в игре с угадыванием местоположения горошины, оптимальной, а не только лучшей из списка, является стратегия под номером 4. По своей сути максимизация гарантированного выигрыша аналогична жизненному кредо тех людей, которые всегда склонны рассчитывать на худшее, но при этом все еще пытаются как-то улучшить свое положение в жизни.

Задача о «случайном» трамвае приобретает свой окончательный вид

Формализм

Чтобы воспользоваться принципом максимизации гарантированного выигрыша, представьте, что судьба играет с вами в игру: она раз за разом посылает вас в неизвестный город, расположенный в какой-то неизвестной вселенной, ждет пока вы не повстречаете там первый трамвай, а затем вопрошает, сколько же в этом городе всего трамвайных маршрутов. Будем считать, что ваш ответ считается приемлемым и игра заканчивается в вашу пользу, если только названное вами число отличается менее чем в два раза от истинного, причем как в большую, так и в меньшую стороны. Будем также считать, что это очень долгая партия игр, длинною в целую жизнь.

Теперь вполне правомерно задать вопрос: «Какая стратегия в описанной игре будет для вас оптимальной в том смысле, что сможет обеспечить максимальное число гарантированно приемлемых ответов?»

Подробный анализ простейших стратегий

В качестве «первого боя» с только что поставленной задачей попытаемся выяснить, насколько хороши для нее наивные стратегии »x1» и »x2».

Итак, судьба забросила нас в очередной незнакомый нам город. Как и прежде, буква $N$ обозначает количество трамвайных линий в этом городе. По условию все числа от $1$ до $N$ с равной вероятностью могут оказаться номером маршрута $k$ , по которому будет следовать первый подмеченный нами трамвай.

Согласно стратегии »x1» оценкой $V$ для числа $N$ должно быть само $k$ . Понятное, что $k$ никогда не будет больше $N$ , поэтому не может оказаться так, чтобы $V$ была больше $2N$ . Следовательно наша оценка будет неприемлемой только в одном случае: если $V$ , то есть $k$ , окажется меньше, чем $N/2$ . Вероятность получить $k$ меньшее $N/2$ при нечетных $N$ не превосходит 50%, а при четных — равна им. Отсюда следует, что при использовании стратегии »x1» в очень длинной партии игр по крайней мере (примерно) половина сделанных оценок гарантированно окажутся приемлемыми, какой бы там сценарий не уготовила судьба.

Теперь предположим, что мы решили использовать стратегию »x2». По правилам этой стратегии, увидев на трамвае номер $k$ , мы должны в качестве $V$ назвать число $2k$ . Как и в предыдущем случае, наша оценка никогда не превзойдет $2N$ , и поэтому неприемлемой она будет считаться только при одном условии, если ее значение меньшее, чем $N/2$ . В то же время, $V$ будет меньше $N/2$ , только если номер трамвая $k$ окажется меньше, чем $N/4$ . Вероятность последнего события для городов с $N$ кратным 4-ем равна $1/4$ , а для остальных городов — и того меньше. Следовательно, если мы решаем придерживаемся стратегии »x2», то тем самым обретаем гарантию, что в любой долгой партии игр по крайней мере (примерно) ¾ всех наших ответов окажутся приемлемы независимо от того, насколько превратно поведет себя с нами судьба.

Сквозь тернии к звездам

Перед тем, как приступить к главной части повествования, где мы займемся поисками оптимальных стратегий, я слегка видоизменю условия задачи и буду считать, что $N$ , $V$ и $k$ могут теперь принимать не только натуральные, но и любые действительные значения, большие нуля. Этот шаг необходим, чтобы избавиться от связанных с дискретностью надоедливых оговорок и скучного перебора особых случаев. Конечно, сейчас еще трудно представить себе город, в котором есть трамваи со всеми номерами от 0 до π, однако этого вам и не понадобится. У нашей задачи в ее новой непрерывной модификации имеется простая и вполне реалистичная модель.

Представьте себе, что некто взял полоску фотографической пленки длинной $N$ см и решил пронаблюдать за тем, как на ней будут оставлять свой след приходящие из космоса частицы. В масштабах эксперимента плотность вероятности попадания частиц на пленку будет описываться равномерным распределением на отрезке $[0,\,N]$ . В этом опыте экспериментатор сообщает вам расстояние $k$ между левым краем пленки и точкой, куда угодила первая зарегистрированная частица. Как и прежде, от вас требуется дать приемлемую оценку $V$ для неизвестного вам $N$ , то есть такую оценку, которая отличается от $N$ не более чем в два раза, как в большую, так и в меньшую стороны. Как и прежде, судьба ведет с вами долгую партию игр, каждый раз решая, каково будет $N$ в очередной игре.

В качестве простого упражнения покажите, что несмотря на изменившиеся условия стратегия »x1» по-прежнему гарантирует вам примерно 50%, а стратеги »x2» — все те же примерные 75% приемлемых оценок соответственно, вне зависимости от того, какой сценарий выберет судьба.

Долгий путь к совершенству

Предварительный отсев

Наконец-то все приготовления завершены и в этом параграфе мы можем заняться поисками оптимальных стратегий. Для простоты, правда, мы будем рассматривать не все стратегии, а ограничимся теми, в которых оценка $V$ представима, как $f(k)$ , где $f()$ — это некоторая действительнозначная функция, определенная на интервале $(0,\ +\infty)$ .

Представьте теперь, что в одном эксперименте расстояние от места попадания частицы до левого края фотопленки было равным $k_1$ , а в другом эксперименте — $k_2$ , причем $k_1<k_2$ . Не будет ли тогда разумным, длине фотопленки в первом эксперименте дать меньшую оценку, чем во втором. Если так, то из неравенства всегда должно следовать неравенство $f(k_1)<f(k_2)$ , другими словами, функция $f()$ должна быть строго возрастающей. Не менее разумным выглядит предположение, что для «близких» по значению $k_1$ и $k_2$ оценки $V_1=f(k_1)$ и $V_1=f(k_2)$ тоже должны быть близки, то есть, функция $f()$ должна быть непрерывной.

Если проанализировать, какие ответы мы считаем приемлемыми, то получится еще одно
ограничение на $f()$ . Смотрите, в нашем понимании задачи $V$ приемлема в том (и только в том случае), когда $N/2\le f(k)\le2N$ . Расстояние $k$ между засвеченным космической частицей пятном и левым краем фотографической пленки никогда не превосходит длину пленки $N$ , отсюда непосредственным образом получаем неравенство: $2k\le2N$ . Из последнего неравенства следует, что было бы неразумно, узнав от экспериментатора расстояние $k$ , оценивать $N$ числом $V$ меньшим $2k$ . Действительно, если мы увеличим оценку $V$ до $2k$ , то тем самым точно не сделаем ее чрезмерно большой, однако в тех случаях, когда $V$ изначально была неприемлемо малой, подобное переопределение способно ее даже «исправить». Таким образом, в процессе поиска оптимальных стратегий нам достаточно рассмотреть только те функций $f(k)$ , значения которых при всех $k>0$» /> подчинены неравенству<br /><img src= .

Ее величество формула

Сейчас мы займемся тем, что для произвольной стратегии постараемся выразить величину гарантируемого ею выигрыша в виде некой общей аналитической формулы.

Итак, в очередном эксперименте по регистрации космических частиц используется фотопленка длины $N$ , $k$ — удаление точки попадания первой частицы от ее (пленки) левого края, а $V=f(k)$ — наша оценка для $N$ . Пусть эксперименту только предстоит состояться, какова тогда вероятность, что $V$ окажется приемлемой по отношению к $N$ ? Самое большое значение $V$ , когда она еще считается приемлемой, — это $2N$ , самое маленькое — $N/2$ .

Поскольку $f()$ строго возрастает и непрерывна, то существует обратная к ней функция $f^{-1}\left(v\right)$ , которая также строго возрастает и непрерывна. Для значений $f()$ всюду выполняется неравенство $f(k)\geq2k$ , поэтому для значений $f^{-1}()$ должно выполнятся двойственное неравенство: $f^{-1}\left(v\right)\le 1/2 v$ (рис 1)

Рис. 1

Теперь нетрудно сообразить, что максимальным значением $k$ , дальше которого $V$ становится уже неприемлемо большой, является $k_{sup}=f^{-1}\left(2N\right)$ . Это следует из того, что $f^{-1}\left(\right)$ строго возрастает и $k_{sup}=f^{-1}\left(2N\right)\le 2N$ . Аналогично, минимальным значением $k$ , меньше которого $V$ становится неприемлемо малой, является $k_{inf}=f^{-1}\left(N/2\right)$ . Из двух последних утверждений следует, что $V$ будет приемлемой по отношению к $N$ в том (и только в том) случае, если расстояние $k$ между засвеченным пятном и левым краем пленки окажется заключенным между $k_{inf}$ и $k_{sup}$ . Вероятность последнего события, обозначим ее как $p_{success}(f,\ N)$ , равна:

$\frac{k_{sup}-\ k_{inf}\ }{N}$

или более подробно:

$p_{success}(f,\ N)=\ \frac{f^{-1}\left(2N\right)-\ f^{-1}\left(N/2\right)\ }{N}$

Должно быть очевидно, что наихудшим для для $f$ сценарием будет последовательность таких экспериментов, в каждом из которых длинна фотографической пленки $\bar{N}$ минимизирует значение $p_{success}(f,\ N)$ . Отсюда следует, что в очень длинных последовательностях экспериментов доля приемлемых ответов, гарантированная оценкой $f(k)$ , будет даваться выражением:

${\rho\left(f\right)={inf}_N[\ p}_{success}(f,\ N)]$

Теперь мы можем утверждать, что любая оптимальная стратегия должна максимзировать $\rho\left(f\right)$ , другими словами, $\varphi(k)$ будет оптимальной в том и только в том случае, если:

${inf}_N[p_{success}\left(\varphi,\ N\right)]={sup}_f\ {inf}_N[p_{success}\left(f,\ N\right)]$

.
Итак, проблема отыскания оптимальных оценок свелась к вопросу о том, как выглядит функция $\varphi(k)$ , которая доставляет выражению

$(*)\ \ \ \ \ \ inf_N\left[\frac{f^{-1}\left(2N\right)-f^{-1}\left(N/2\right)}{N}\right]$

максимум в классе всех непрерывных строговозрастающих функций, определенных
на интервале $(0,+\infty)$ , графики которых лежат не ниже $l(k)=\ 2k$ . Не правда ли, что в такой постановке задача может показаться пугающе сложной? Я думаю, для вас это прозвучит неожиданным, но ответ на нее изысканно прост. Давайте вместе попытаемся его угадать.

Искусство правдоподобных рассуждений

Пожалуй, самое простое, с чего можно начать — это выяснить, какая из функций вида $f(k)=\ \lambda\cdot k$ (здесь $\lambda$ — любое действительное число ≥2) доставляет выражению (*) самое большое значение. Обратной для $f(k)=\ \lambda\cdot k$ служит функция $f^{-1}\left(v\right)=\lambda^{-1}\cdot v$ , подставляя ее в выражение для $p_{success}$ , имеем:

$p_{success}\left(N,\lambda\right)=\ \frac{\lambda^{-1}\cdot2N-\lambda^{-1}\cdot N/2}{N}=\frac{3}{2}\ \cdot\ \lambda^{-1}\$

Как вы видите, $p_{success}$ не зависит от $N$ и принимает тем большее значение, чем меньшим по величине было $\lambda$ . Таким образом, в классе функций $f(k)=\ \lambda\cdot k$ , $\lambda\geq2$ наибольшее значение выражению (*), придает уже знакомая нам по функция $l(k)=\ 2k$ .

Давайте теперь подумаем, что произойдет, если отсчитывать расстояние не в сантиметрах, а, скажем, метрах, дюймах или световых годах — как тогда изменится вид функции $\varphi$ оптимальной оценки?

Пусть в сантиметрах оценка $V$ имеет вид $V_{cm}=\ f_{cm}(k_{cm})$ , а $V_m$ и $k_m$ — те же самые величины, выраженные в метрах, тогда:

$V_m=\frac{1}{100}V_{cm}=\frac{1}{100}f_{cm}({100\cdot k}_m)=\ f_m(k_m)$

В общем случае мы будем иметь дело со шкалой длин $A$ и шкалой длин $B$ , которая получается из $A$ умножением на коэффициент $\mu_{AB}$ . Каждая оценка $V(k)$ может быть вычислена как в единицах шкалы $A$ , так и в единицах шкалы $B$ . Пусть $f_A(k_A)$ — ее представление в единицах шкалы $A$ , а $f_B(k_B)$ — представление в единицах шкалы $B$ , тогда:

$f_B(t)=\mu_{AB}\cdot f_A({\mu_{AB}}^{-1}\cdot t)$

Вид последнего уравнения говорит о том, что функции $f_A(t)$ и $f_B(t)$ скорей всего различны ( $t$ в данном случае — это действительная переменная с нейтральным смыслом).

Как вы считаете, правдоподобно ли, что мы и какой-нибудь представитель далекой космической цивилизации получим для решаемой здесь задачи разные ответы лишь потому, что у нас с ним разные единицы измерения длины? Наверное, нет! Отсюда следует, что для любого $$\mu>0$» /> и любой функции <img src=$ , которая максимизирует выражение $(*)$ , функция $\psi(t)=\mu\cdot\varphi(\mu^{-1}\cdot t)$ также должна максимизировать $(*)$ . Если вдруг $\varphi(t)$ является единственной оптимальной для $(*)$ функцией, то при всех $t>0$» /> и <img src=

Положив в этом тождестве $\mu=t$ , мы тем самым находим вид функции $\varphi$ :

$\varphi(t)=t\cdot\varphi(t^{-1}\cdot t)=t\cdot\varphi(1)$

Смотрите, что выходит: если все наши многочисленные предположения верны, то оптимальная функция $\varphi(t)$ принадлежит классу функций $f(k)=\ \lambda\cdot k$ , но ранее мы уже выяснили, что внутри указанного класса максимальное значение выражению $(*)$ придает функция $l(k)=\ 2k$ . Неужели оптимальной стратегией является »x2»?

Строгие выводы: оптимальность x2

Хорошо, у нас есть много намеков на то, что оценка, заданная функцией $l(k)=\ 2k$ , является оптимальной. Давайте докажем эту гипотезу строго, а еще установим, при каких условиях других оптимальных оценок нет.

Возьмем произвольную непрерывную строго возрастающую функцию $f(k)$ , удовлетворяющую неравенству $f(k)\le2k$ , фиксируем некоторое $v_0$ из области ее значений и попытаемся для начала выяснить, какой геометрический смысл скрывается за величиной $p_{success}\left(f,\ v_0\right)$ .

Рис. 2

Если на графике функции $f^{\left(-1\right)}\left(v\right)$ отметить точки $A=({v_0/2,\ f}^{-1}(v_0/2))$ и $B=({{2v}_0,\ f}^{-1}({2v}_0))$ (рис 2), а затем соединить их отрезком, то тангенс угла наклона этого отрезка к оси $Ov$ будет выражаться формулой

$\frac{f^{-1}\left(2v_0\right)-f^{-1}(v_0/2)}{3/2\ \cdot\ v_0}$

то есть по сути будет равен $2/3$ -ям от $p_{success}\left(f,\ v_0\right)$ . То же самое наблюдение можно выразить несколько иначе: для этого нужно на отрезок $AB$ посмотреть как на график некоторой функции $i(v)$ . Внутри интервала $(v_0/2,\ 2v_0)$ функция $i(v)$ имеет, очевидно, постоянную производную и $p_{success}\left(f,\ v_0\right)$ равен $3/2$ -ым ее величины.

Теперь уже не сложно показать, что функция $f(k)$ не может превзойти $l(k)=\ 2k$ по величине инфинума $p_{success}$ , иными словами, стратегия »x2» оптимальна.

Рассуждения я начну с двух предварительных замечаний:

$f(k)\geq2k= l(k)$ , поэтому $f^{\left(-1\right)}\left(v\right)\le l^{-1}\left(v\right)=1/2\cdot v$ то есть график функции $f^{\left(-1\right)}\left(v\right)$ лежит не выше графика $l^{-1}\left(v\right)$
величина значения $p_{success}\left(l,\ v\right)$ не зависит от и равна , производная $l^{-1}\left(v\right)$ во всех точках равна .

Чтобы потом прийти к противоречию, сначала предположим, что $f(k)$ строго лучше $l(k)$ . Последнее возможно только в том случае, если существует некоторое $$\varepsilon>0$» /> и при всех <img src=$ выполняется неравенство: $p_{success} (f,v)≥3/4 + ε$ .

Для какого-нибудь $u_0>0$» /> отметим на графике функции <img src= последовательность точек

$B_0=(u_0/2,\ f^{\left(-1\right)}\left(u_0/2\right)),\ B_1=(2u_0,\ f^{\left(-1\right)}\left(u_0\right)),\ B_2=(8u_0,\ f^{\left(-1\right)}\left(8u_0\right)),\ ...$

, соединим их ломанной $B_0\ B_1B_2...B_n...$ и интерпретируем эту ломанную как график кусочно-линейной функции $I(v)$ . В последовательности $u_0/2,\ 2u_0,\ 8u_0, \ldots\$ каждое последующее значение в 4 раза больше предыдущего, поэтому на каждые два идущие друг за другом числа мы можем смотреть, как на некое $v_0/2$ и © Habrahabr.ru