Симулятор мозга II26.07.2022 19:16

Здравствуйте, предлагаю обзор и разбор проекта Brain Simulator II от Чарльза Дж. Саймона, основателя FutureAI. Этот проект и компания малоизвестны, в русскоязычном сегменте интернета вообще нет никаких упоминаний о ней. Моё внимание компания привлекла благодаря сообщению о том, что недавно FutureAI привлекла 2 миллиона $ инвестиций. Проект оказался для меня очень любопытным и интересным, так как я сам во многом разделяю взгляды на проблематику создания AGI Чарльза Саймона, и у меня была практика создания симулятора подобного Brain Simulator II. Обзор проводится на основе общедоступных материалов с сайта FutureAI.guru, откуда можно свободно скачать сам симулятор (windows), а также найти ссылку на его исходный код (c#). Ниже будет представлен вольный перевод одной из статей с сайта, в сопровождении моих комментариев.

Чарльз Дж. Саймон признанный на национальном уровне предприниматель, разработчик программного обеспечения и менеджер. Обладает широким управленческим и техническим опытом, а также научными степенями в области электротехники и компьютерных наук, имеет многолетний опыт работы в IT, включая уникальный опыт работы в области искусственного интеллекта и САПР. Родом из Сан-Франциско, Калифорния, г-н Саймон стал соучредителем трех новаторских технологических компаний, где участвовал в качестве президента и вице-президента по инженерным вопросам. Его технический опыт включает создание двух уникальных систем искусственного интеллекта, а также программного обеспечения для оборудования по проведению неврологических тестов. Сочетание разработки искусственного интеллекта с биомедицинским тестированием нервных сигналов дает ему уникальные видение принципов работы мозга.

Использование отдельных нейронных спайков для репрезентации информации

Чарльз Дж. Саймон (источник).

Большая часть нервного возбуждения в коре мозга представляет собой случайные отдельные спайки, в среднем один раз в несколько секунд. Возникает вопрос: как может система из кажущихся случайных отдельных спайков представлять полезную информацию и приводить к общему интеллекту, демонстрируемому человеческим мозгом? Почти все искусственные нейронные сети представляют информацию в виде частоты срабатывания нейронов и хранят память в весовых коэффициентах синапсов. Кодирование частоты импульсов наблюдается в сенсорных и моторных нейронах, но анализ энергии показывает, что для подобного кодирования для большинства нейронов коры потребовалось бы значительно больше энергии. Также, веса синапсов хороши для кодирования долговременной памяти, но если учитывать время необходимое для перестройки синапса, то оно слишком велико, чтобы объяснить кратковременную память. В этой статье представлены смоделированные нейронные механизмы, которые могут преобразовывать сигналы основанные на частоте в сигналы представляющие собой отдельные спайки, и наоборот отдельные спайки в сигналы основанные на частоте. Затем обсуждается несколько механизмов кратковременной памяти и представления знаний в форме одиночных спайков. Это цифровая модель представляет собой другой подход к решению основных проблем ИИ. В совокупности эти алгоритмы представляют собой возврат к истинным нейроморфным методам как подходу продвижения к сильному искусственному интеллекту (AGI). Наконец, эти алгоритмы и методы существенно влияют на оценку количества информации, которую может обрабатывать человеческий мозг, и, как следствие, снижают требуемые вычислительной мощности, необходимой для создания AGI.

Современное программное обеспечение искусственного интеллекта, основанное на нейронах, основано на концепции, согласно которой частота возбуждения нейронов является представлением передаваемой информации. Энергетический анализ мозга показывает, что менее 1% нейронов в неокортексе активируются достаточно часто, чтобы представлять такие сигналы. Соответственно, мозг должен представлять информацию в виде, казалось бы, случайных отдельных спайков и коротких серий импульсов. В этой статье описываются методы преобразования частотных сигналов в одиночные параллельные сигналы с одним спайком и предлагаются нейронные схемы для обработки информации, а также ответы на некоторые базовые вопросы ИИ.

Эти методы представляют собой новое направление в исследований ИИ, отличное от ИНС/(обратного распространения ошибки), но более общее и нейроподобное, чем символьные подходы ИИ. Совместно, эти методы могут создать любую желаемую функциональность и объединить информацию от нескольких органов чувств, чтобы имитировать функциональность, базовую для интеллекта. Кроме того, эффективность этих подходов может сделать возможным сильный искусственный интеллект (AGI) на современном оборудовании, что окажет глубокое влияние на общество.

Все примеры в этом тексте, а также симулятор, использованный для их создания, находятся в свободном доступе для скачивания и проверки.

Паттерны нейронных спайков можно условно разделить на частотные, серийные и отдельные спайки. Сигналы, основанные на частоте, определенно присутствуют в зрительных и других сенсорных нейронах, а также в двигательных нервах. В то время как большинство нейронных моделей искусственного интеллекта сосредоточены исключительно на кодировании информации в частоте возбуждения нейронов, энергетический анализ неокортекса показывает, что этот тип передачи сигналов находится в меньшинстве. 

Значения в нижеследующих расчетах подвержены большим количеством экспериментальных данных. Расчет выполняется со значениями «наилучшей оценки», как показано на рисунке, за которыми следует диапазон ожидаемых результатов.

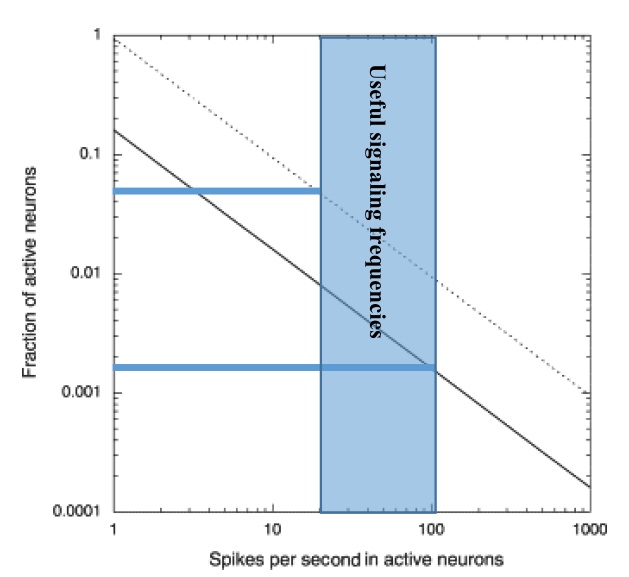Незакрашенная часть из P. Lennie, «The cost of cortical computing». Доля активных нейронов рассчитывается двумя способами: первый (сплошная линия) основан на наилучших оценках доступности и стоимости энергии, а второй (пунктирная линия) основан на оценках, стремящихся минимизировать потребление энергии. Заштрихованная область полезных сигнальных частот дает диапазон доли активных нейронов неокортекса от 0,05 до 0,002.

16 миллиардов нейронов неокортекса срабатывают с наилучшей оценкой в среднем 0,16 Гц (один раз каждые шесть секунд), генерируя 2,56×109 нейронных импульсов в секунду [K. Grace, ed, «Neuron firing rates in humans»]. Это число основано на измеренном общем потреблении энергии неокортексом, деленным на расчетную энергию, затрачиваемую отдельными нейронами и синапсами при возбуждении. Эта низкая средняя частота возбуждения часто упускается из виду, потому что экспериментатор, исследующий нейроны, обычно интересуется нейронами, которые возбуждаются, и склонен игнорировать нейроны, которые не возбуждаются в интересующий период времени.

NRate, NBurst и NSingle представляют количество нейронов зависящие от частоты, серии (череда импульсов) и одиночных спайков соответственно.

NRate + NBurst + NSingle = 16×109 нейронов

R * NRate + B * NBurst + NSingle = 2.56×109 спайков/с

Где R — средняя частота импульсов для сигналов с частотным представлением при использовании частоты 20 Гц (см. «Максимальная и минимальная частоты импульсов» на рисунке выше). B — количество импульсов в пакете, при этом используется 10.

С двумя уравнениями и тремя неизвестными конкретного решения нет, но поскольку количество нейронов не может быть отрицательным, максимальное значение NRate равно 128×106 (оставляя 0 для двух других категорий). Если мы уменьшим NRate до 127×106, то у нас останется 16×109 нейронов, которые представляют собой пакетные или одиночные нейроны, поскольку 127×106 меньше, чем предел погрешности. При расчете в этом примере у нас осталось около 1,4×109 нейронов, активирующихся сериями импульсов, и 14×109 отдельными импульсами.

127×106 представляет собой поразительно малую долю 0,8% нейронов неокортекса, кодирующих информацию частотами срабатывания. Остальные нейроны будут возбуждаться со средней частотой один импульс каждые 266 секунд — слишком медленно для большинства наблюдений.

На рисунке выше показан разумный диапазон возможных долей возбуждения нейронов в полезном частотном диапазоне от 5% до 0,2%.

Поскольку в подавляющем большинстве мы можем наблюдать нервные импульсы в виде коротких серий или одиночных импульсов, то большая часть вычислений в мозге, основанных на частоте, сосредоточена на входах сенсорных сигналах и создании моторных сигналов, которые, как известно, также основаны на частоте.

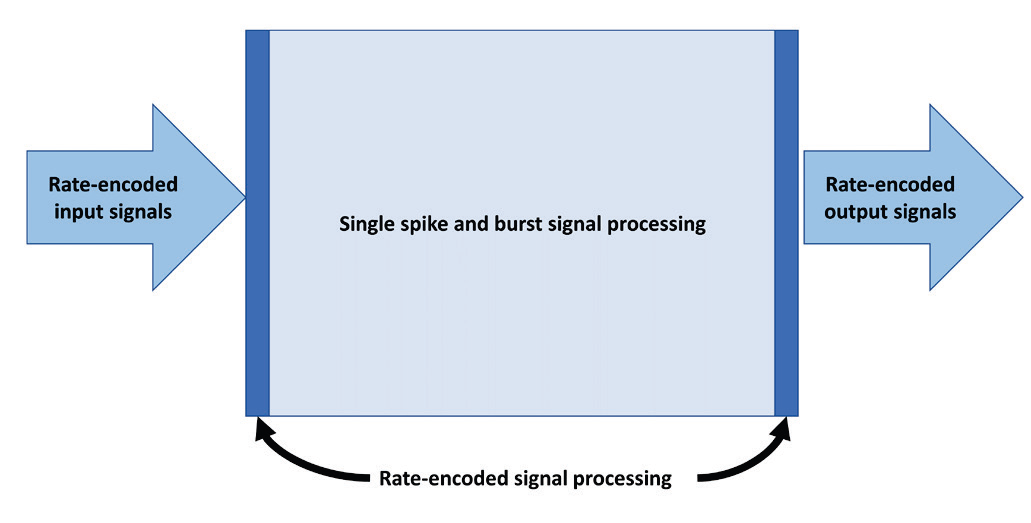Это схематическое изображение иллюстрирует небольшое количество кодированного по частоте сигналов на входах и выходах, окружающая большой объем вычислений, основанных на одиночных или серийных импульсах.

Максимальная и минимальная частота срабатывания нейронов

Биологические нейроны могут срабатывать с максимальной частотой около 200 Гц. После срабатывания наступает рефрактерный период, в течение которого никакая стимуляция не заставит нейрон снова возбудиться, что и устанавливает максимальную частоту активаций. Сигнал, изменяющийся во времени, будет иметь максимальную среднюю частоту 100 Гц. В течение рефрактерного периода ионы, используемые возбужденным нейроном, транспортируются обратно, поэтому процесс может повторяться бесконечно. Этот ионный транспорт требует незначительного количества энергии, но, помноженный на миллиарды нейронов в мозге, составляет ~12 Вт энергии, потребляемой мозгом. 

Минимальная частота срабатывания ограничена базовым представлением того, как часто или как быстро последовательность спайков должна представлять минимальный уровень сигнала. Рассмотрим представление тонов, участвующих в восприятии речи, где, как известно, присутствует кодирование сигналов на основе частоты. Люди могут говорить (и понимать речь) со скоростью более десяти слогов в секунду. Исходя из этого, мы можем предположить, что все поступающие слуховые сигналы должны передавать значение менее чем за 0,1 с. Это устанавливает минимальную полезную частоту срабатывания на уровне 10 Гц с минимальной средней частотой срабатывания 20 Гц.

Модель нейронов

Оставшаяся часть этой статьи демонстрирует, как нейроны потенциально могут представлять важную информацию в одиночных спайках. Нет никаких ожиданий, что все эти методы существуют в биологическом мозге, но некоторые из них вероятны. Нейронное моделирование, используемое для разработки схем в следующих примерах, было создано с помощью Brain Simulator II.

Разбирая идею отдельных спайков репрезентирующих информацию, необходимо использовать модели, основанные на спайках. Моделирование проводилось с помощью моделей нейронов IF (Integrate-and-Fire, «накапливай и активируйся») и LIF (Leaky Integrate and Fire, «накапливай и активируйся с утечкой»). В обеих моделях нейроны накапливают воздействие от входящих нервных импульсов до тех пор, пока не будет достигнут порог, а затем испускают один импульс. Но в модели LIF накопленное воздействие уменьшается по экспоненциальному закону. Когда нейрон активируется, выходные синапсы, соединяющие его с другими нейронами, вносят вклад в суммирующие воздействие этих нейронов на величину веса синапса.

Обе модели более правдоподобны с биологической точки зрения, чем модели с ИНС постоянного действия. Доступны более биологически точные модели, но в данном обсуждении используются модели IF и LIF, более биологически точные модели выходят за рамки представленных здесь схем, поэтому они не будут полезными. Кроме того, используемые здесь модели отличаются от биологических в двух важных аспектах: 1) время является дискретным, а не непрерывным, и 2) все спайки достигают нейронов-мишеней одновременно. Эти различия не умаляют полезности моделей.

В общем, спаковые модели более эффективны с вычислительной точки зрения, чем общие модели ИНС, поскольку вычисления требуются только тогда, когда нейрон срабатывает. Поскольку мы рассматриваем нервный импульс как редкое событие, вычислительная эффективность возрастает еще больше.

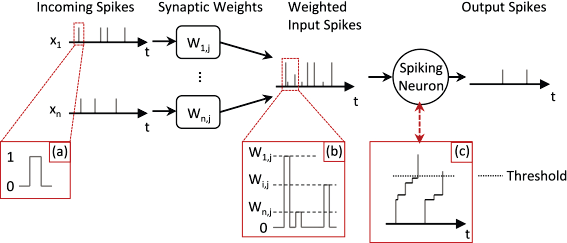Модель импульсного нейрона значительно отличается от типичной модели ИНС тем, что она накапливает воздействие от асинхронных входящих импульсов и выдает один импульс при достижении порога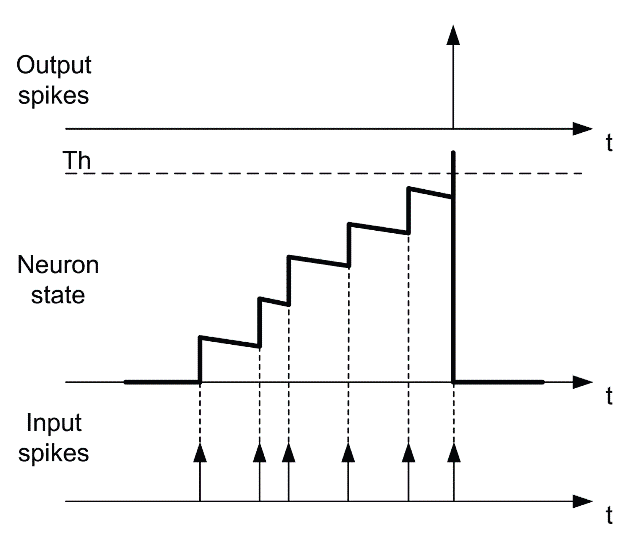Модель LIF накапливает импульсы с утечкой, уменьшающей заряд нейрона во время между пиками. Не показано: тормозные синапсы с отрицательным весом, которые могут напрямую уменьшать заряд

Следующие уравнения определяют функцию модели LIF, реализованную в моделировании.

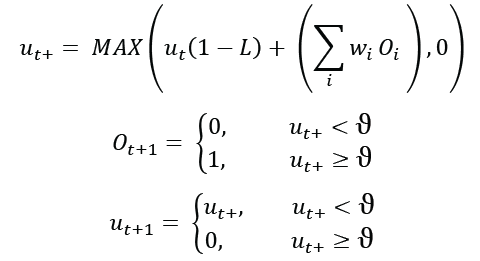
Где ut — потенциал мембраны нейрона в момент времени t.  ut+ — промежуточное значение. L — скорость утечки, диапазон от 0 до 1.

© Habrahabr.ru