Шифруем по-русски, или отечественные криптоалгоритмы01.12.2020 18:18

В данной статье простыми словами описаны криптоалгоритмы, являющиеся актуальными на данный момент российскими стандартами защиты информации, и подобраны ссылки на материалы, которые при желании помогут разобраться с ними глубже. А также, в конце статьи приведены работы с результатами криптоанализа одного из важнейших элементов данных алгоритмов.

Из новостей

За ближайший год не раз появлялись новости о предложениях расширять области использования отечественной криптографии. Чтобы представить сроки реализации предложений, стоит упомянуть ряд новостей.

До конца 2020 года планируется «закончить создание национального удостоверяющего центра — структуры, которая будет выдавать сайтам в Рунете отечественные цифровые сертификаты», пишет Медуза. Также, по данным этого издательства отечественные цифровые сертификаты будут использовать криптоалгоритмы Магма и Кузнечик. Кроме того, отечественные алгоритмы шифрования по требованию Центробанка станут обязательными к использованию в платежных системах уже с 2024 года, пишет РБК.

Добавим к этому новость от газеты Коммерсантъ, в которой Магма и Кузнечик упоминаются в контексте тестируемых алгоритмов для использования в виртуальных сим-картах eSim.

Упомянутые выше и другие основные алгоритмы, используемые в отечественной криптографии стандартизованы и описаны в ГОСТах.

Направления ГОСТов

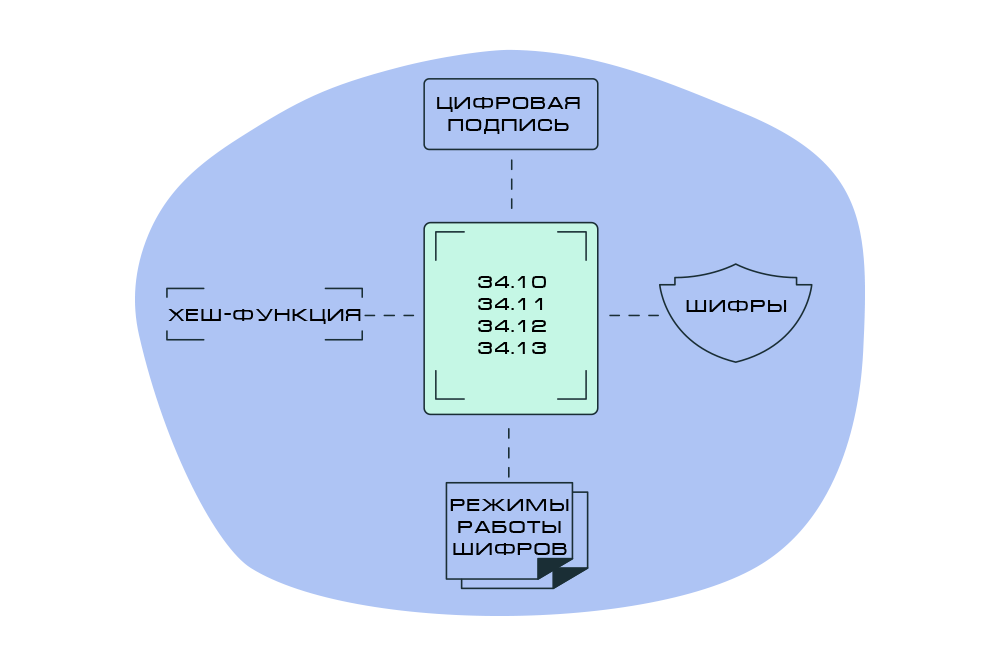
Отечественная криптография базируется на четырех основных объектах, которые мы рассмотрим далее.

Цифровая подпись

ГОСТ 34.10–2018 описывает алгоритмы формирования и проверки электронной цифровой подписи с помощью операций в группе точек эллиптической кривой и функции хеширования. Длины секретного ключа 256 бит и 512 бит.

У пользователя есть сообщение, ключ подписи и ключ для проверки подписи. Ключ проверки подписи является открытым, для того, чтобы любой получатель смог расшифровать и убедиться в достоверности подписи. То есть если получателю удается расшифровать сообщение с помощью открытого ключа проверки подписи, принадлежащего определенному отправителю, то он может быть уверен, что сообщение подписывалось ключом подписи именно этого отправителя.

В алгоритмах формирования и проверки электронной цифровой подписи важным шагом является вычисление точки на эллиптической кривой, поэтому, прежде чем переходить к самим алгоритмам, приведем используемые понятия.

Эллиптической кривой над конечным простым полем F_p , где p>3» src=«https://habrastorage.org/getpro/habr/upload_files/730/bb9/0d7/730bb90d714c9038e3c7e3c094b1e436.svg» />, называется множество точек <img alt= , $x,y\ \epsilon\ F_p$ , удовлетворяющих уравнению (в форме Вейерштрасса) $y^2 = x^3 + ax + b (mod\ p)$ , где $4a^3+27b^2 \neq0$ , $a,\ b\ \epsilon\ F_p$ .

Альтернативный способ задать эллиптическую кривую

Отметим, что эллиптическую кривую можно задать уравнением не только в форме Вейерштрасса. Относительно новым способом задания эллиптической кривой является уравнение в форме Эдвардса $x^2 + y^2 = 1+dx^2y^2, d\ \epsilon \ F_p\backslash \{ 0,1 \}$ .

Суммой точек , эллиптической кривой называется точка (x_3,y_3) , координаты которой определяются, как $x_3 = \lambda^2 -x_1 -x_2(mod\ p)$ , $y_3 = \lambda^2(x_1 -x_3) -y_1(mod\ p)$ , где $\lambda = \frac{y_2 - y_1}{x_2-x_1} (mod\ p)$ .

Точка эллиптической кривой C = kP , может быть определена через сумму точек C = P+P+...+P .

Разбор теории, необходимой для криптографии на эллиптических кривых, можно найти тут.

Алгоритмы формирования и проверки электронной цифровой подписи.

Подпись создается по следующему алгоритму.

входные данные: сообщение и закрытый ключ подписи .

— к сообщению применяется хеш-функция (Стрибог) и вычисляется хеш-код сообщения h=h(M) , отметим, что хеш-код — это строка бит.

— определяется число $e = \alpha(mod\ q)$ , где $\alpha$ — целое число, которое соответствует двоичному представлению хеш-кода . Причем если $\alpha(mod\ q) = 0$ , то принимается за 1.
— это порядок порядок циклической подгруппы группы точек эллиптической кривой, который является одним из параметров цифровой подписи. Также среди параметров есть — это базовая точка подгруппы.

— на основе случайно сгенерированного целого числа k, 0<k<q , это число называют секретным ключом. Затем вычисляется точка на эллиптической кривой C = kP . Точка имеет координаты (x_c,y_c) .

— из координаты точки на эллиптической кривой и преобразования хеша вычисляется электронная подпись (r, s) , где $r = x_c (mod\ q),\ s = (rd+ke)(mod\ q)$ . Если либо , либо равняется 0, то нужно вернуться к предыдущему шагу.

выходные данные: цифровая подпись (r, s) которую добавляют к сообщению.

Теперь перейдем к алгоритму проверки подписи.

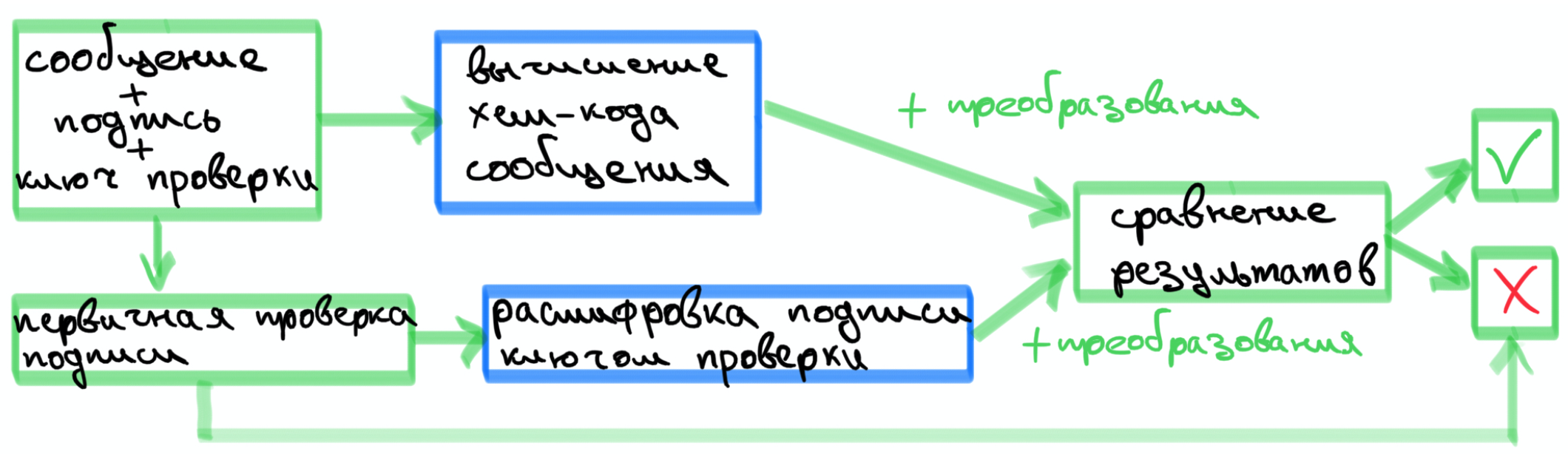
входные данные: сообщение c цифровой подписью (r, s) и ключ проверки подписи

— полученная цифровая подпись проходит первичную проверку, если проверка не пройдена, то есть не выполнены неравенства $0<r<q,\ 0<s<q$ , то подпись неверна.

— вычисляется хеш-код сообщения h=h(M) , опять же с помощью алгоритма Стрибог.

— определяется число $e = \alpha(mod\ q)$ , где $\alpha$ целое число, которое соответсвует двоичному представлению хеш-кода. Причем если $\alpha(mod\ q) = 0$ , то принимается за 1. Затем определяется $\nu = e^{-1}(mod\ q)$ .

— вычисляется точка эллиптической кривой $C = s\nu P -r\nu Q$ , из которой получается $R = x_c (mod\ q)$ .

— если r = R , то подпись верна

выходные данные: подпись вена/неверна

Хеш-функция

ГОСТ 34.11–2018 посвящен функции хеширования. В данном документе содержится описание алгоритма вычисления хеш-функции, известной из предыдущих версий стандарта, как Стрибог.

Стрибог принимает на вход сообщение произвольной длины, которое впоследствии разбивается на блоки размером 512 бит (с дополнением блоков при необходимости). После чего входные данные преобразуются в хеш-код фиксированной длинны 256 или 512 бит.

Подробное описание алгоритма вместе с разбором используемых в нем преобразований можно найти в статье @NeverWalkAloner.

Шифры

ГОСТ 34.12–2018 охватывает блочные шифры. Именно в этом ГОСТе описаны алгоритмы шифрования Кузнечик и Магма — алгоритмы блочного шифрования с длинами шифруемых блоков 128 бит и 64 бита соответсвенно и длиной ключа шифрования 256 бит у обоих.

Шифрование блока открытого теста Кузнечиком происходит в 10 раундов, для каждого раунда из исходного ключа шифрования генерируется пара раундовых ключей, в каждом раунде проходят стадии подстановки и перестановки (перестановка вызывает особый интерес для криптоанализа алгоритма).

Приведем упрощенную схему работы Кузнечика при зашифровании.

Расшифрование Кузнечиком реализуется путем использования обратных операций подстановки и перестановки в инвертированном порядке, также, в обратном порядке следуют и раундовые ключи.

@sevastyan01 в своей статье подробно описал алгоритм Кузнечик.

Зашифрование блока Магмой проходит в 32 раунда, для каждого раунда из исходного ключа шифрования генерируется раундовый ключ, причем алгоритм генерации ключей отличается от генерации ключей в Кузнечике.

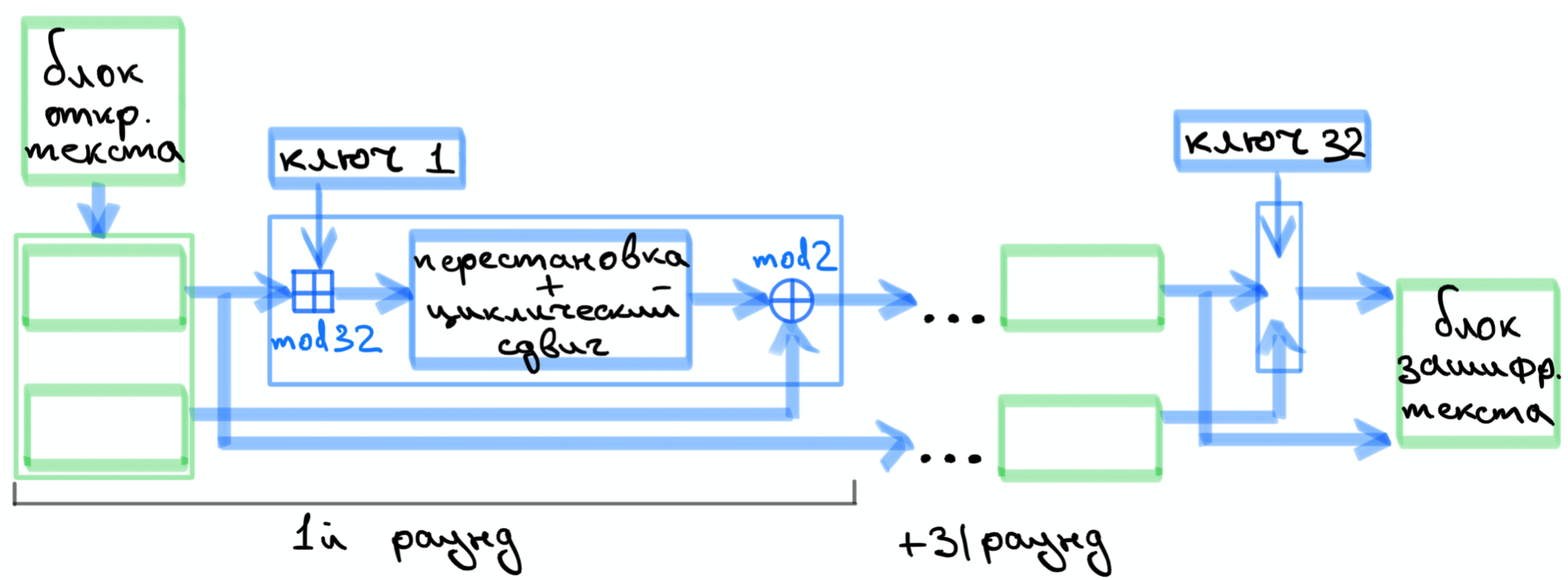
Расшифрование производится аналогичной зашифрованную последовательностью раундов, но с инвертированным порядком следования раундовых ключей.

Режимы работы шифров

ГОСТ 34.13–2018 содержит описание следующих режимов работы блочных шифров.

Режим простой замены

При зашифровании сообщение делится на блоки равной заданной длины. В случае, когда размер сообщения не кратен размеру блока, последний блок дополняется до нужной длины. Каждый блок независимо от остальных шифруется функцией, выполняющей блочное шифрования с использованием ключа.

Расшифрование происходит аналогичным образом. Причем если при зашифровании было применено дополнение, то при расшифровании применяется обратная операция.

Режим гаммирования

В данном режиме работы при шифровании каждый блок открытого текста складывается с блоком гаммы путем операции побитового сложения по модулю 2, XOR. Под гаммой понимается зашифрованная с использованием ключа последовательность, которую вырабатывает определенный алгоритм, который принимает на вход вектор инициализации.

Схематично изобразим данный режим при зашифровании и расшифровании, они происходят аналогично друг другу.

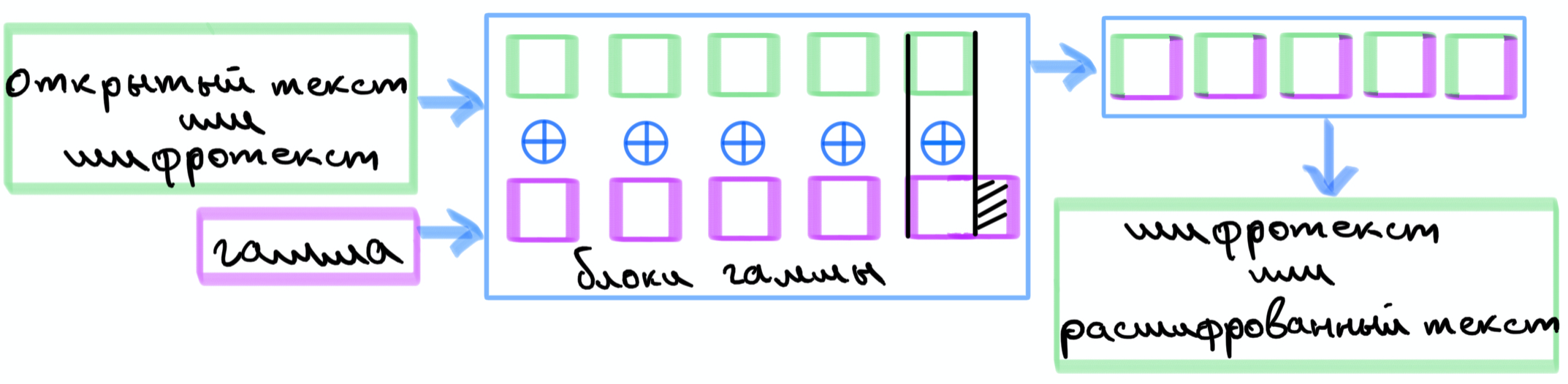
Если общая длина гаммы не кратна длине блока, то последний блок гаммы усекается до размера блока. Блоки гаммы отличны друг от друга и имеют псевдослучайных характер.

Режимы гаммирования с обратной связью: по выходу, по шифротексту

Два режима помещены в один пункт, так как они похожи между собой. В данных режимах при зашифровании выходные данные процедуры шифрования, либо сам шифротекст в случае обратной связи по шифротексту, подаются на вход следующей процедуре шифрования и так далее.

Отличие режимов можно увидеть на схеме.

При расшифровании схема преобразуется следующим образом. Шифротекст встает на место открытого текста, процедура шифрования сменяется процедурой расшифрования, а выходом алгоритма является расшифрованный текст. В дальнейших схемах будем это учитывать.

Режим простой замены с зацеплением

Особенностью данного режима работы является то, что каждый блок открытого текста, за исключением первого, складывается с предыдущим результатом шифрования.

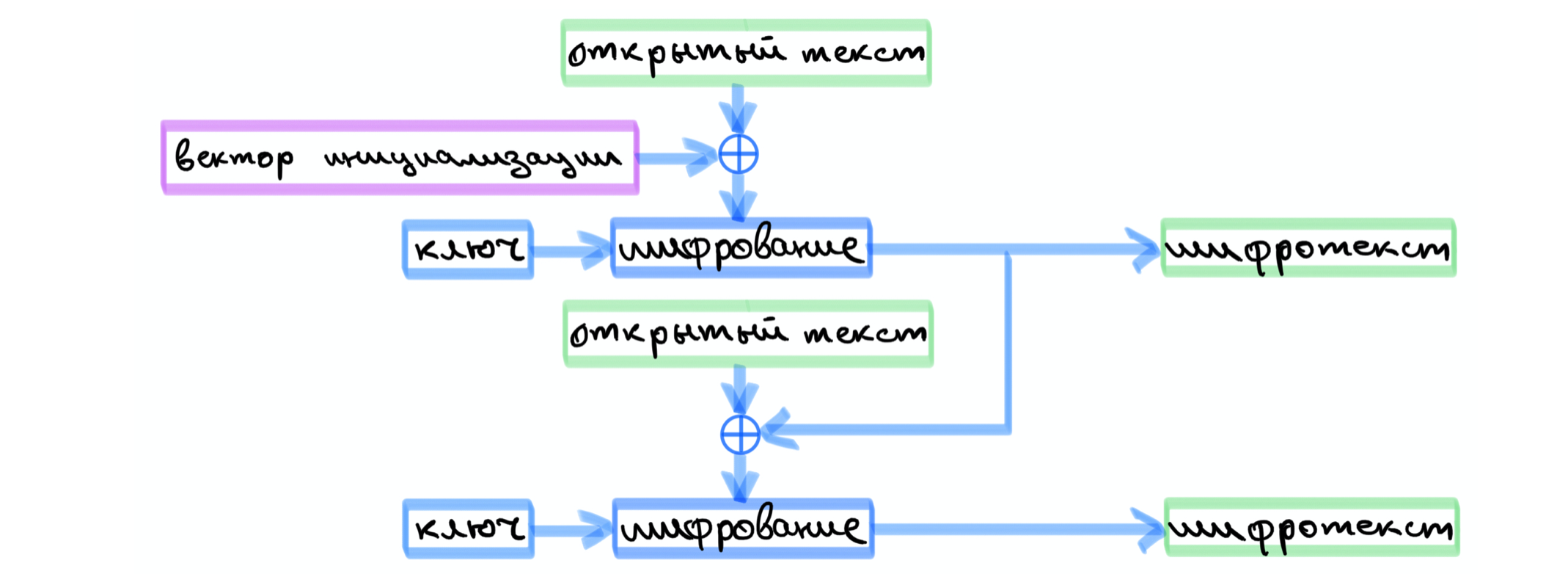
Режим выработки имитовставки

При работе в данном режиме создается зависящий от всего текста блок, который предназначен для проверки наличия в шифротексте искажений.

Каждый из стандартов действителен с 1 июня 2019 года в соответствии с приказом Федерального агентства по техническому регулированию и метрологии. Актуальные ГОСТы наследуют разработки, прописанные в предыдущих версиях.

Реализации алгоритмов ГОСТов

@ru_crypt в своей статье собрал множество вариантов реализации ГОСТовских алгоритмов на любой вкус.

Интерес к таблице подстановок

Рассмотрим ГОСТ 34.10–2018. В алгоритмах формирования и проверки цифровой подписи на начальных шагах используется хеш-функция Стрибог, которая определена в ГОСТ 34.11–2018.

Заглянем теперь в ГОСТ 34.12–2018. В данном документе в качестве параметра алгоритма Кузнечик для нелинейного биективного преобразования приводится таблица подстановок

$\pi$ . Эта же таблица приведена в ГОСТ 34.11–2018, то есть используется и при хешировании.

Таблица $\pi$ задает единственное нелинейное преобразование в алгоритме шифрования, которое значительно усложняет взлом шифра. То есть функция подстановки особенно важна для устойчивости шифра к взломам.

Разработчики Кузнечика и Стрибога утверждают, что сгенерировали таблицу $\pi$ случайным образом. Однако в ряде работ был проведен криптоанализ таблицы подстановок и выявлено несколько способов ее генерации, причем не случайным образом.

Статьи с алгоритмами генерации таблицы $\pi$ :

Reverse-Engineering the S-Box of Streebog, Kuznyechik and STRIBOBr1 — Alex Biryukov, L ́eo Perrin, and Aleksei Udovenko

Exponential S-Boxes: a Link Between the S-Boxes of BelT and Kuznyechik/Streebog — Léo Perrin and Aleksei Udovenko

Partitions in the S-Box of Streebog and Kuznyechik — Léo Perrin

В конце каждой из статей приведены алгоритмы генерации таблицы подстановок, которые можно запустить в оригинальном виде с помощью SageMath.

Заключение

В данной статье мы познакомились с основными криптоалгоритмами, которые приняты в качестве стандартов ГОСТ и получили базовое представление об их работе. А также, привели примеры работ по криптоанализу Кузнечика и Стрибога.