SamsPcbCalc, часть 2: Сколько тепла может рассеять печатная плата?
С совершенствованием элементной базы всё меньше энергии уходит в тепловую: снижается сопротивление транзисторов в открытом состоянии, растут частоты импульсных преобразователей напряжения. Но от задачи теплоотвода в рамках текущей полупроводниковой парадигмы никуда не деться, тот же рост производительности при увеличении степени интеграции уже приводит к пределу плотности тепловыделения. Для микросхем с мощностью тепловых потерь более 1 Вт тепловая задача важна не меньше, чем электрическая. Нужно ли отводить тепло на корпус? Или использовать радиатор для микросхемы? Для ответа на эти вопросы не всегда требуется моделирование тепловой задачи с помощью КЭМ. В этой статье рассматриваем достаточно гибкую модель, которая позволяет быстро получить предварительную оценку теплового сопротивления «плата-среда» с хорошей точностью.
О важности тепловой задачи можно судить по упрощённому эмпирическому правилу, гласящему, что каждое повышение температуры на 10 оС снижает срок наработки до отказа в 2 раза. То есть, если при 55 оС микросхема проработает 10 лет, то при 65 оС только 5. Достаточный аргумент, чтобы несколько улучшить теплоотвод от микросхемы, если не играть в запланированное устаревание. Это правило — далеко не истина в последней инстанции, но качественно оно верно (подробнее можно прочитать, например, здесь).
Организация теплоотвода это почти всегда накладной процесс, который усложняет трассировку, поэтому его нужно планировать заранее. Для этого нужно понимать, сможет ли сама печатная плата справиться теплоотводом. Производители микросхем указывают в документации параметр тепловое сопротивление «кристалл-среда» RθJA. Казалось бы:

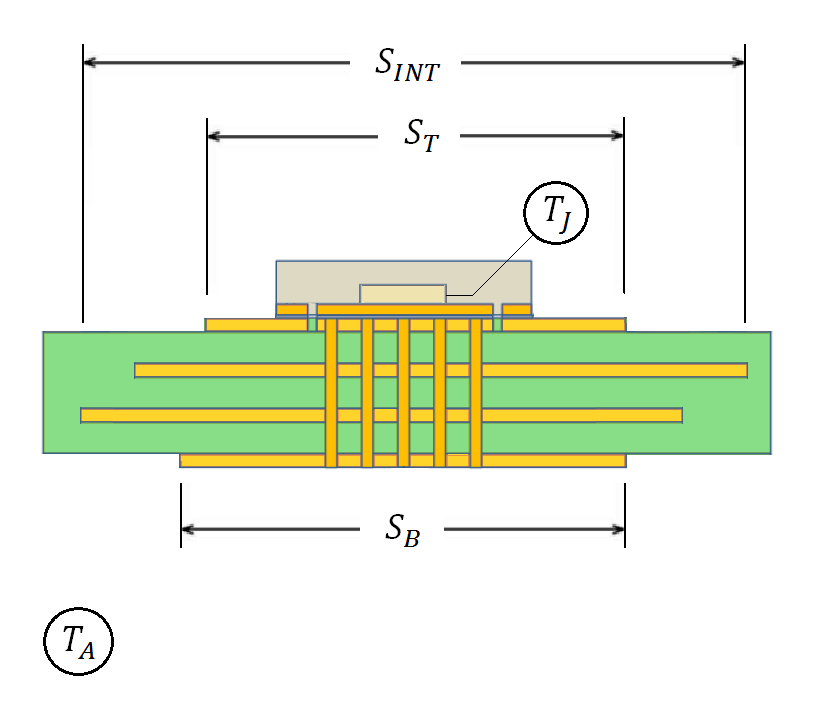
и оценка готова. Но это грубо, очень грубо. Тепловое сопротивление сильно зависит от печатной платы. И то, что указано, было получено в эксперименте на стандартизованной печатной плате (например, как на рисунке 1), которая, скорее всего, будет сильно отличаться от той, что получится у Вас. Скажем так, можно получить гораздо лучший теплоотвод при меньшей площади.

То, на что стоит обращать внимание — это тепловое сопротивление «кристалл-плата» RθJB или RθJС (bottom). Это то, что уже от разработчика не зависит и определяется корпусом и его внутренней конструкцией. Но тут чаще всего выбор корпуса определяется мощностью тепловых потерь, и основной перепад температур будет на плате. Итак, вышеуказанную формулу для случая теплоотвода через плату переписываем так:

где RθBA — тепловое сопротивление печатной платы с заданными параметрами. Рассчитать это сопротивление можно на основе красивой модели, которая предложена в которую можно извлечь из замечательной статьи от ON Semiconductor. Статья, на самом деле, не является пошаговой инструкцией, это своего рода набросок модели. Мне пришлось её раз 10 прочитать, чтобы прийти к модифицированной модели, которую в итоге и реализовал в калькуляторе на своей платформе. В основе расчетов лежит чёткая математическая модель (описана вот в этой публикации от тех же ON Semiconductor) тепловой задачи однородного кольца, через внутреннюю поверхность которого гонится поток тепла. Теплоотвод — за счёт конвекции, то есть это не про вакуум (там тепло нужно гнать на корпус). Схема задачи на рисунке 2, а дифференциальное уравнение и интересующая нас часть его решения следующие:


Всё с этим уравнением прекрасно (кроме модифицированных функций Бесселя), и можно решать для одной поверхности с конвекцией (убрав »2» в корне), но вот только платы чаще всего без радиальной симметрии и не однородные, а ещё и тепло поступает неравномерно по внутреннему радиусу. Поэтому нужно адаптировать. Первые два вопроса решаются разбиением на кольцевые зоны с однородными свойствами с той же площадью. Для решения последнего нужно строить приближённую модель цепи тепловых сопротивлений. На рисунке 3 — то, что предлагалось в оригинальной статье. Предлагается бить плату на три зоны: зону под микросхемой, зону с полигонами на внешнем слое и зону только с полигонами на внутренних слоях. Учитываются только проводники, которые непосредственно соединены с микросхемой, (условно, «звонятся»).

Верхний и нижний полигоны предлагается усреднить и взять среднюю площадь металлизации. С этим я не очень согласен, так как влияние на теплоотвод у этих слоёв очевидно разное, плюс они могут сильно отличаться по площади (нижний чаще будет больше по площади). Поэтому я разбил плату на верхнюю и нижнюю половины и делал расчёт для каждой части отдельно.
В статье много графиков с влиянием различных параметров, их полезно посмотреть. Свой подход к разбиению платы откалибровал на этих графиках (рисунок 4) — они для корпусов QFN5×5, QFN6×6 и QFN3×3, соответственно. Когда плата очень большая, график «ложится» на предел, связанный с тепловым сопротивлением переходных отверстий, но их параметры не указаны. Я брал диаметр 450 мкм, толщину стенок 20 мкм, без заполнения.



Видно, что модели коррелируют, но добиваться 100% совпадения я не стал, так как всё равно нет всех входных данных. Кроме того, есть странный момент с переходными отверстиями (рисунок 5), их отсутствие практически не влияет на тепловое сопротивление, что не очень интуитивно.
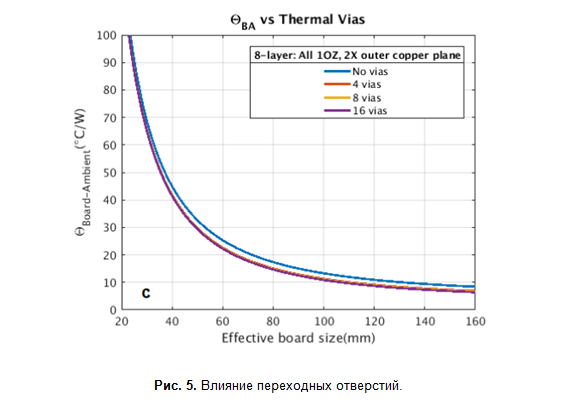
Ещё на нижнем графике на рисунке 4 видно два ряда данных, где я считал двухзонную модель двумя методами: с помощью умножения матриц, как описано в статье AND8222/D, и с помощью модели, как на рисунке 3, только зона под микросхемой выброшена (она не вносит вклад в сопротивление). Видно, что график из статьи выходит на примерно ту же асимптоту, как будто отсутствует влияние переходных отверстий. Это для меня стало ещё одним фактором, что в их модели что-то не так с учётом влияния переходных отверстий (либо я чего-то не понимаю).
Калькулятор оказался полезным хотя бы в том плане, что позволил от качественных представлений о влиянии различных параметров перейти к количественным оценкам. Можно сделать вывод, что тепловое сопротивление платы можно загнать в район 10 оС/Вт даже на стационарном воздушном потоке. Для рассеивания 2–3 Вт вполне достаточно будет. Ещё полезное замечание, что значимую роль при теплоотводе играет только металл, непосредственно соединённый с микросхемой. Хотя, конечно, чем больше объёмная доля меди в плате, тем будет выше эффективный коэффициент теплопроводности. На основе этого калькулятора можно нарастить наличие радиатора на микросхеме и теплоотвод на корпус, это тоже буду делать. Если там будет что-то интересное, то поделюсь в следующих публикациях.
