RSA простыми словами и в картинках
Ассиметричный алгоритм криптографии RSA, датой возникновения концепции которого считается 1976 год сейчас очень активно используется для обмена данными, верификацией источника программного обеспечения и в других сферах, где необходимо обмениваться данными или верифицировать отправителя. Кроме того, он является базовой частью HTTPS протокола, использование которого в России достигло 98% по данным Яндекс.Радара.
Например, звоня любимой бабушке через популярный мессенджер или вводя данные своей банковской карточки в онлайн маркетплейсе, перед обменом видеоизображением или данными банковской карты, происходит процедура проверки подлинности и обмена ключом шифрования по алгоритму RSA.
Но что же это за алгоритм такой и как он работает? В этой статье я постараюсь разложить по полочкам основные принципы его работы и ассиметричной криптографии в целом.
RSA ключи и шифрование данных
В отличии от симметричных алгоритмов шифрования, имеющих всего один ключ для шифрования и расшифровки информации, в алгоритме RSA используется 2 ключа — открытый (публичный) и закрытый (приватный).
Публичный ключ шифрования передаётся по открытым каналам связи, а приватный всегда держится в секрете. Но зачем нужно целых два ключа и как они работают?
В ассиметричной криптографии и алгоритме RSA, в частности, публичный и приватный ключи являются двумя частями одного целого и неразрывны друг с другом. Для шифрования информации используется открытый ключ, а для её расшифровки приватный.
Предположим, Боб хочет передать Алисе какое-то сообщение, но лично он это сделать не может, поэтому ему необходимо использовать посредника, например Стива. Однако Боб передаёт Алисе информацию про сюрприз для Стива на его день рождения, так что не может допустить, чтобы Стив это сообщение увидел. И тут ему пригодится протокол RSA.
Перед обменом сообщением, Боб просит у Алисы её открытый ключ
После получения ключа, переданного через Стива, Боб шифрует своё сообщение ключом Алисы
Далее Боб, через Стива, передаёт Алисе зашифрованное сообщение
Алиса расшифровывает сообщение своим закрытым ключом
Таким образом, Стив видел открытый ключ Алисы и зашифрованное сообщение от Боба, но без закрытого ключа Алисы это сообщение не расшифровать. То есть, пусть Стив и держал в руках все передаваемые данные, но он не может узнать, что Боб передал Алисе!
Наглядная схема:

RSA шифрование сообщений
Вы можете задаться вопросом, а почему Стив не может подменить ключ Алисы на свой, расшифровать сообщение, а потом, подглядев его, зашифровать обратно на ключ Алисы? Ещё как может, это называется атака «человек посередине» (Man in the middle (MITM)), и выглядит она следующим образом:

MITM
Но есть ли решение этой проблемы? Да! Chain of Trust, или «Цепочка доверия»
Подпись данных и цепочка доверия
Перед тем как разбирать что такое «Цепочка доверия», нужно знать про ещё одну возможность закрытого ключа — подпись информации. Она осуществляется с помощью закрытого ключа и проверяется открытым.
То есть, если Боб и Алиса заранее обменялись своими открытыми ключами, они могут писать друг другу сообщения и прикреплять к ним некий набор данных. Если взять этот набор данных, открытый ключ и само сообщение, можно проверить действительно ли сообщение было отправлено собеседником и не подменил ли его кто-то по дороге.

RSA подпись данных
С функцией подписи закрытого ключа разобрались, действительно полезная штука! Но как это решает проблему человека по середине, ведь если Боб и Алиса не могут без посредников обменяться открытыми ключами, Стив может подменить их при передаче и постоянно перехватывать сообщения?
А всё просто! Поскольку, с помощью закрытого ключа можно подписать какие-то данные, с его помощью можно подписать и сам открытый ключ.
Если есть кто-то, предположим Грант, которому Боб и Алиса могут доверять и чей открытый ключ у них уже есть, то Грант может подписать их открытые ключи. Таким образом, если Стив попытается подменить открытый ключ Алисы, которая посылает его Бобу, то Боб сразу обнаружит подмену, ведь на ключе не будет подписи Гранта.
Также Грант может подписать открытый ключ Марку, который подпишет открытые ключи Боба и Алисы, создав таким образом ту самую «цепочку доверия».
В реальном мире существуют доверенные корневые центры сертификации (Грант), промежуточные центры (Марк) и конечные получатели (Боб и Алиса).

Chain of Trust
Компрометация ключей и списки отзыва
А теперь предположим, что Алиса оставила на виду свой закрытый ключ, его увидел Стив и теперь может подписывать любые сообщения, а также перехватывать и расшифровывать все данные, которые шифруются на открытый ключ Алисы. Такая проблема называется «Компрометация ключа».
На такой случай, умные люди придумали «список отзыва» (Certificate Revocation List (CRL)), в котором будут публиковаться скомпрометированные ключи, к которым больше нет доверия.
Адрес, где находится такой список отзыва встроен во все сертификаты корневых и промежуточных центров сертификации. То есть, если Алиса заподозрит, что Стив увидел её закрытый ключ, она должна будет немедленно сказать от этом Марку, который опубликует номер её сертификата в своём списке отзыва. Боб со своей стороны, при получении старого сертификата, которым попытается воспользоваться Стив, найдёт запись о его отзыве в списке Марка и будет понимать, что Алиса была скомпрометирована и доверять её старому сертификату уже нельзя.
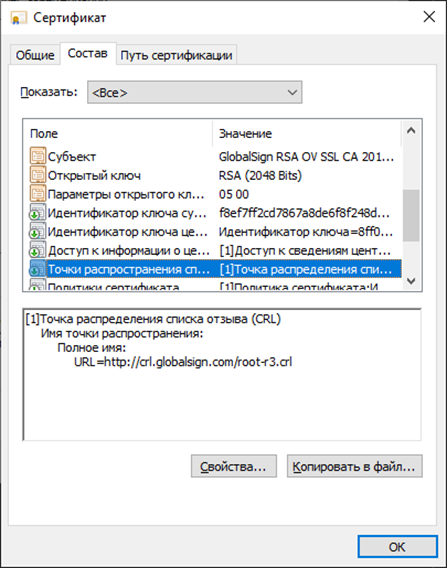
CRL в сертификате
Под капотом
С базовыми аспектами RSA алгоритма разобрались, теперь давайте заглянем «под капот» и посмотрим, как работает эта магия.
Вся ассиметричная криптография держится на принципе «в одну сторону быстро, в другую неразумно долго».
Например, если мы перемножим числа 592939 и 592967 мы получим число 351593260013. Но как имея только число 351593260013 узнать числа 592939 и 592967? А если каждое из этих двух чисел будут длинной более 1000 знаков? Это называется «сложность задачи факторизации произведения двух больших простых чисел», т.е. в одну сторону просто, а в обратную невероятно сложно.

Теперь рассмотрим процедуру создания публичного и приватного ключей:
Выбираем два случайных простых числа p и q
Вычисляем их произведение: N = p * q
Вычисляем функцию Эйлера:
(N) = (p-1) * (q-1)
Выбираем простое число e, которое меньше
(N) и является и является взаимно простым с
(N) (не имеющих общих делителей друг с другом, кроме 1)
Ищем число d, обратное числу e по модулю
(N) .Т.е. остаток от деления (d*e) и
(N) должен быть равен 1
После произведённый вычислений, у нас будут:
e и n — открытый ключ
d и n — закрытый ключ
А теперь создадим эти ключи на примере малых простых чисел:
Пусть p = 19, q = 41
Получается:
{691, 779} — открытый ключ
{571, 779} — закрытый ключ
Ключи мы с вами вычислили, теперь перейдём к шифрованию сообщений.
Предположим, что Боб спрашивает у Алисы во сколько сегодня вечеринка. Алиса знает, что вечеринка в 21, но что ей нужно сделать чтобы передать это Бобу так, чтобы Стив об этом не узнал?
Для этого Алисе необходимо знать открытый ключ Боба, возьмём его из предыдущих вычислений {691, 779}. Далее ей нужно возвести сообщение в степень e (691) по модулю n (779), а Бобу потом нужно будет возвести полученное от Алисы число в степень d (571) по модулю n (779). Давайте изобразим это наглядно

Заключение
Мы рассмотрели основные аспекты криптографического алгоритма RSA, однако многое осталось за кадром, надеюсь у меня получилось достаточно понятно объяснить, как это работает даже тем, кто очень далёк от криптографии и подобных вещей.
Также рекомендую почитать пару интересных статей на тему криптографии от коллег с Хабра:
Первые несколько миллисекунд HTTPS соединения — про то, как работает криптография работает на сайтах
Доступно о криптографии на эллиптических кривых — альтернатива RSA
Полное руководство по переходу с HTTP на HTTPS — о том как настроить HTTPS у себя на сайте
Let’s Encrypt выдал миллиард сертификатов — о том как Let’s Encrypt помогает обезопасить интернет
