Расчёт сопел современных ракетных двигателей20.01.2018 17:33

7dvcxbrs_3ysevl65fg2i8ptpc8.png

Введение


Сопло ракетного двигателя- техническое приспособление, которое служит для ускорения газового потока, проходящего по нему до скоростей, превышающих скорость звука. Основные виды профилей сопел приведены на рисунке:

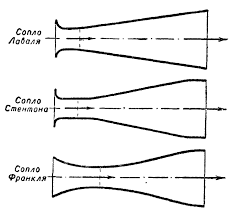
xl-3g6wc2a9nkea7pjtkafogzsi.png

По причине высокой эффективности ускорения газового потока, нашли практическое применение сопла Лаваля. Сопло представляет собой канал, суженный в середине. В простейшем случае такое сопло может состоять из пары усечённых конусов, сопряжённых узкими концами:

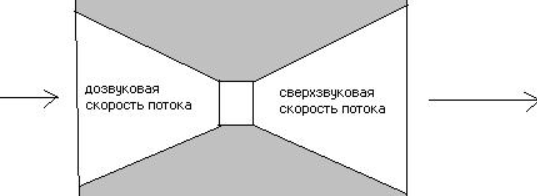
qtfizuiwe03m7zk3t3axlvocofy.png

В ракетном двигателе сопло Лаваля впервые было использовано генералом М.М. Поморцевым в 1915 году. В ноябре 1915 года в Аэродинамический институт обратился генерал М.М. Поморцев с проектом боевой пневматической ракеты.

Ракета Поморцева приводилась в движение сжатым воздухом, что существенно ограничивало ее дальность, но зато делало ее бесшумной. Ракета предназначалась для стрельбы из окопов по вражеским позициям. Боеголовка оснащалась тротилом.

В ракете Поморцева было применено два интересных конструктивных решения: в двигателе имелось сопло Лаваля, а с корпусом был связан кольцевой стабилизатор. Подобные конструкции используются и в настоящее время, но уже с твёрдотопливным двигателем и системой автоматического наведения:

150pnkt8shdq2agec5akrpi49qc.png

Однако проблемы остались старые, но уже в современном исполнении: ограниченная дальность до 3 км., наведение и удержание цели в условиях хорошей видимости, что для настоящего боя не реально, не защищённость от электромагнитных заградительных помех и, наконец, но не в последнюю очередь, высокая стоимость.

Теоретические основы


Эффективные сопла современных ракетных двигателей профилируются на основании специальных газодинамических расчётов. Основное уравнение, связывающее градиент площади сечения, градиент скорости и число Маха, следующее:

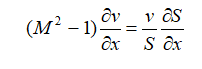
oeepghgrepg27rnmqgxzkichtl4.png

где: S — площадь сечения сопла; v — скорость газа; M — число Маха (отношение скорости газа в какой-либо точке потока к скорости звука в этой же точке).

Анализируя это соотношение, получаем, что в сопле Лаваля могут осуществляться следующие режимы течения:

1) M <1 – поток на входе дозвуковой: [1]
а) 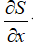mpt8bsu_b6evx-ypyzyv1ljuwfi.png<0, тогда 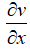nshsweqapokkqcqjwnwnsr2wxay.png>0 (из уравнения). Дозвуковой поток в сужающемся канале ускоряется.
б) 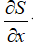mpt8bsu_b6evx-ypyzyv1ljuwfi.png >0, тогда 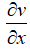nshsweqapokkqcqjwnwnsr2wxay.png<0. Дозвуковой поток в расширяющемся канале тормозится.
2) M>1 — поток на входе сверхзвуковой:
а) 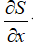mpt8bsu_b6evx-ypyzyv1ljuwfi.png<0, тогда 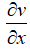nshsweqapokkqcqjwnwnsr2wxay.png<0. Сверхзвуковой поток в сужающемся канале тормозится.
б) 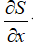mpt8bsu_b6evx-ypyzyv1ljuwfi.png>0, тогда 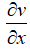nshsweqapokkqcqjwnwnsr2wxay.png>0. Сверхзвуковой поток в расширяющемся канале ускоряется.
3) 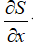mpt8bsu_b6evx-ypyzyv1ljuwfi.png = 0 — самое узкое место сопла, минимальное сечение.
Тогда возможно либо М = 1 (поток переходит через скорость звука), либо 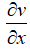nshsweqapokkqcqjwnwnsr2wxay.png = 0 (экстремум скорости).

Какой из режимов реализуется на практике, зависит от перепада давлений между входом в сопло и окружающей средой.

Если давление, достигаемое в критическом сечении, превышает наружное давление, то поток на выходе из сопла будет сверхзвуковым. В противном случае он остается дозвуковым. [2]

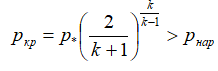eahaehknrhjrzgixpidahvreooi.png — условие сверхзвукового истечения.

где: p* — давление торможения (давление в камере); pкр — давление в критическом сечении сопла; pнар — давление в окружающей среде; k — показатель адиабаты.

Если известны параметры в камере сгорания, то параметры в любом сечении сопла можно узнать по следующим соотношениям:

давление:

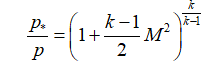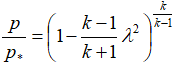i9krbqx6zp3bsjdw5pblllpd-cc.png или mnhtktf86r180hxessfvbilxymg.png;

температуру:

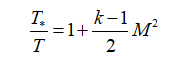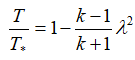c12rlpzvvehe2ohl2x4lqopoh4u.png или cfru2afcm-zm4nvvjvj3rksohr8.png;

плотность:

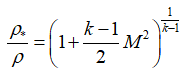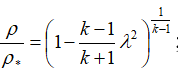f_4vmdrbq9tfaplegp6fj8sxvpy.png или rt5rmhpwabsm3n-tejsamzt70sy.png;

скорость:

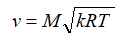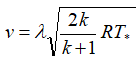o15mkp7emhhpeoexlmcu_ybvnmu.png или zfa2ezjqsycuvrl83y14ovrouie.png.

В этих формулах — λ — приведенная скорость, отношение скорости газа в данном сечении сопла к скорости звука в критическом сечении, R — удельная газовая постоянная. Индексом »*» обозначены параметры торможения (в данном случае — параметры в камере сгорания).

Постановка задачи


1. Рассчитать параметры течения потока газов в сопле Лаваля: для этого профиль сопла Лаваля разбивается на 150 контрольных точек — 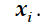2esyjbptryglagut2zrfy6ykbyo.png. Разбиение осуществляем таким образом, чтобы минимальное сечение располагалось в точке 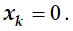tnztvtdn2bavxs2dfdwsxvs2g8w.png. Определяются значения газодинамических функций давления, плотности и температуры в каждом сечении.

2. Расчёты выполнить средствами высокоуровневого свободно распространяемого языка программирования Python по следующей расчётной схеме и исходным данным:

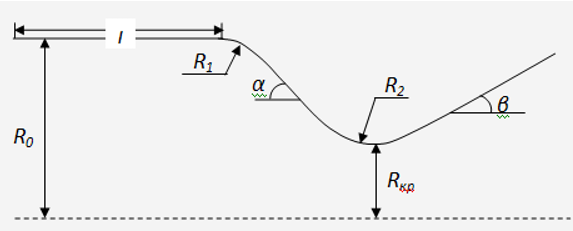
g9ruww6chbgwgn635acqr1h92c8.png

Рисунок 1-Профиль сопла Лаваля

Таблица 1-Исходные данные

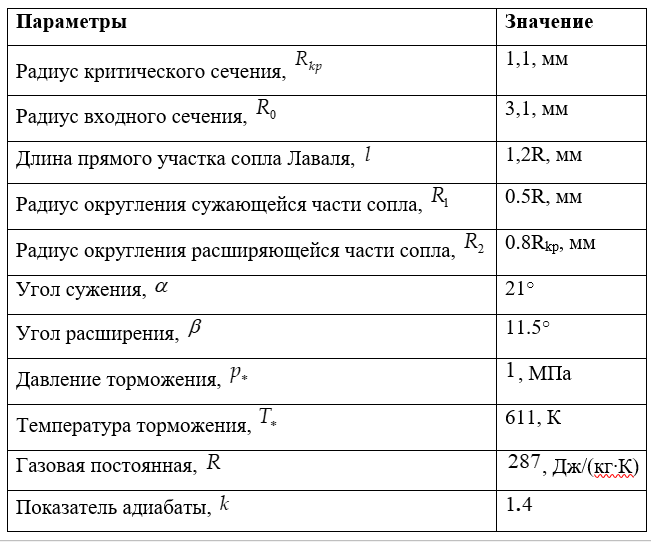
fgmt8gbv4ms06b4mwww4nun5_ww.png

Приведенные исходные данные носят демонстрационный характер.

Расчёт сопла Лаваля средствами Python

Листинг для построения профиля и площади проходного сечения сопла Лаваля
#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
import numpy as np
from math import *
alfa=21.0#Угол сужения
beta=11.5#Угол расширения
rkr=1.1#Радиус критического сечения
R0=2*rkr
r1=0.5*rkr# Радиус округления сужающейся части сопла
r2=0.8*rkr# Радиус округления расширяющейся части сопла
ye=rkr+r2
L=1.2*R0#Длина прямого участка сопла Лаваля
x0=0
y0=R0
xa=L
ya=y0
xc1=xa
yc1=ya-r1
xc=xa+r1*cos(radians(90-alfa))
yc=yc1+r1*sin(radians(90-alfa))
yd=ye-r2*sin(radians(90-alfa))
xd=xc+(yc-yd)/tan(radians(alfa))
xc2=xd+r2*sin(radians(alfa))
xe=xc2
xf=xe+r2*cos(radians(90-beta))
yf=ye-r2*sin(radians(90-beta))
def R(x):     
        if x0<=x<=xa:
               return ya*1e-4
        if xa<=x<=xc:
               return (yc1+sqrt(r1**2-(x-xc1)**2))*1e-4
        if xc<=x<=xd:
               return (-tan(radians(alfa))*(x-xc)+yc)*1e-4
        if xd<=x<=xf:
                return (ye-sqrt(r2**2-(x-xe)**2))*1e-4
        if xf<=x:
                return (yf+tan(radians(beta))*(x-xf))*1e-4     
y=[R(x+xe) for x in np.arange(-5,5,0.01)]
x=np.arange(-5,5,0.01)
plt.figure()
plt.title('Профиль сопла ')
plt.axis([-5.0, 5.0, 0.0, 3.0*10**-4])
plt.plot(x,y,'r')
plt.grid(True)
plt.figure()
plt.title('Изменение площади проходного \n сечения сопла  вдоль его продольной  оси ')
yy=[pi*R(x+xe)**2 for x in np.arange(-5,5,0.01)]
plt.plot(x,yy,'r')
plt.grid(True)
plt.show()

a2eioe70cjz9rpgbtzvwyln6byu.png

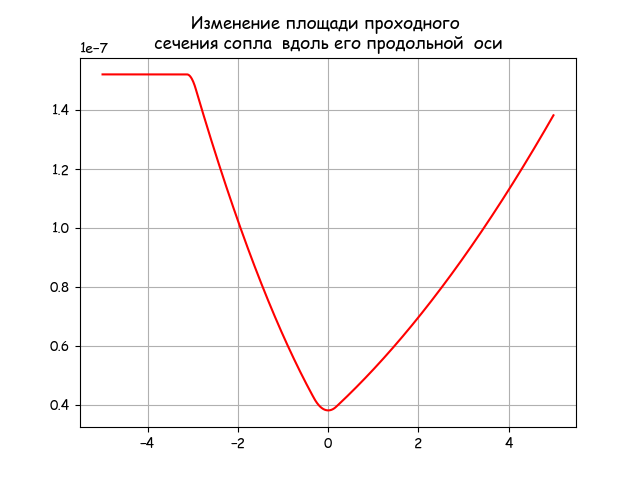
nwf3suaabv3joolrh3jf1aglsdw.png

Для продолжения решения задачи на Python, нужно связать λ — приведенную скорость газа с координатой x вдоль продольной оси. Для этого я воспользовался функцией fsolve из библиотеки SciPy со следующей инструкцией:

fsolve (<функция>, <стартовая точка>, xtol=1.5 · 10^8)

Привожу фрагмент программы для управления решателем с одной стартовой точкой: 

def lamda(z):
         m=round(Q(z),2)
         if z>= 0:                 
                  x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,1.5)
                  return x[0]
         if z<0:
                  x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,0.5)
                  return x[0]

Это единственно возможное на Python решение сложного алгебраического уравнения со степенной функцией от показателя адиабаты k. Например, даже для упрощённого уравнения с использованием библиотеки SymPy, получим недопустимое время расчёта только одной точки: 

from sympy import *
import time
x = symbols('x',real=True)
start = time.time()
start = time.time()
d=solve( 1.5774409656148784068*x *(1.0-0.16666666666666666667*x**2)**2.5-0.25,x)
stop = time.time()
print ("Время работы решателя:",round(stop-start,3))
print(round(d[0],3))
print(round(d[1],3))

Время работы решателя: 195.675
0.16
1.95

Листинг для вычисления газодинамической функции относительной скорости
#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
import numpy as np
from math import *
from scipy.optimize import *
import time
start = time.time()
alfa=21.0#Угол сужения
beta=11.5#Угол расширения
rkr=1.1#Радиус критического сечения
R0=2*rkr
r1=0.5*rkr#Радиус округления сужающейся части сопла
r2=0.8*rkr#Радиус округления расширяющейся части сопла
ye=rkr+r2
L=1.2*R0#Длина прямого участка сопла Лаваля
x0=0
y0=R0
xa=L
ya=y0
xc1=xa
yc1=ya-r1
xc=xa+r1*cos(radians(90-alfa))
yc=yc1+r1*sin(radians(90-alfa))
yd=ye-r2*sin(radians(90-alfa))
xd=xc+(yc-yd)/tan(radians(alfa))
xc2=xd+r2*sin(radians(alfa))
xe=xc2
xf=xe+r2*cos(radians(90-beta))
yf=ye-r2*sin(radians(90-beta))
def R(x):     
        if x0<=x<=xa:
               return ya*1e-4
        if xa<=x<=xc:
               return (yc1+sqrt(r1**2-(x-xc1)**2))*1e-4
        if xc<=x<=xd:
               return (-tan(radians(alfa))*(x-xc)+yc)*1e-4
        if xd<=x<=xf:
                return (ye-sqrt(r2**2-(x-xe)**2))*1e-4
        if xf<=x:
                return (yf+tan(radians(beta))*(x-xf))*1e-4
def S(x):
         return pi*R(x+xe)**2
xg=2*xe
n=150
RG=287 #Газовая постоянная  
Tt=611 #Температура торможения
k=1.4
def tau(x):      
        return 1-(1/6)*x**2
def eps(x):       
        return (1-(1/6)*x**2)**2.5
def pip(x):             
        return 1-(1/6)*x**2
def Q(z):
         return S(0)/S(z)
x=[x0-xe+(i/n)*(xg-x0) for i in np.arange(0,n,1)]
def lamda(z):
         m=round(Q(z),2)
         if z>= 0:                 
                  x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,1.5)
                  return x[0]
         if z<0:
                  x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,0.5)
                  return x[0]
plt.title('Газодинамическая функция приведенной скорости')
y=[lamda(z) for z in x]
stop = time.time()
print ("Время работы программы:",round(stop-start,3))
plt.ylabel('λ(xi)-отношение скорости газа к скорости звука' )
plt.plot(0, 1, color='b', linestyle=' ', marker='o', label='Сужение сопла')
plt.xlabel('xi -координата вдоль оси сопла')  
plt.plot(x,y,'r')
plt.legend(loc='best')
plt.grid(True)
plt.show()

Время работы программы: 0.222

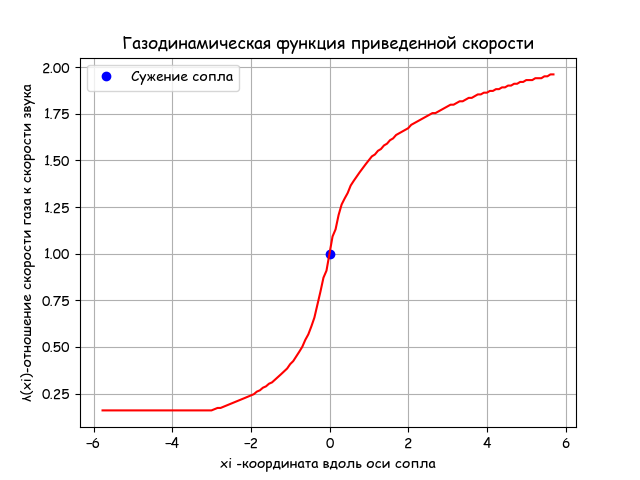
ssr1rto6fnv54lqnpxdiqtfawnm.png

Вывод:

Полученная эпюра распределения скоростей газового потока полностью соответствует изложенной выше теории. При этом, по предложенному алгоритму и библиотеке, время расчёта в 150 точках в 1000 раз меньше, чем для одной точки с использованием solve sympy.

Листинг для вычисления газодинамической функции температуры
#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
import numpy as np
from math import *
from scipy.optimize import *
import time
start = time.time()
alfa=21.0#Угол сужения
beta=11.5#Угол расширения
rkr=1.1#Радиус критического сечения
R0=2*rkr
r1=0.5*rkr#Радиус округления сужающейся части сопла
r2=0.8*rkr#Радиус округления расширяющейся части сопла
ye=rkr+r2
L=1.2*R0#Длина прямого участка сопла Лаваля
x0=0
y0=R0
xa=L
ya=y0
xc1=xa
yc1=ya-r1
xc=xa+r1*cos(radians(90-alfa))
yc=yc1+r1*sin(radians(90-alfa))
yd=ye-r2*sin(radians(90-alfa))
xd=xc+(yc-yd)/tan(radians(alfa))
xc2=xd+r2*sin(radians(alfa))
xe=xc2
xf=xe+r2*cos(radians(90-beta))
yf=ye-r2*sin(radians(90-beta))
def R(x):     
        if x0<=x<=xa:
               return ya*1e-4
        if xa<=x<=xc:
               return (yc1+sqrt(r1**2-(x-xc1)**2))*1e-4
        if xc<=x<=xd:
               return (-tan(radians(alfa))*(x-xc)+yc)*1e-4
        if xd<=x<=xf:
                return (ye-sqrt(r2**2-(x-xe)**2))*1e-4
        if xf<=x:
                return (yf+tan(radians(beta))*(x-xf))*1e-4
def S(x):
         return pi*R(x+xe)**2
xg=2*xe
n=150
RG=287 #Газовая постоянная  
Tt=611 #Температура торможения
k=1.4
def tau(x):      
        return 1-(1/6)*x**2
def eps(x):       
        return (1-(1/6)*x**2)**2.5
def pip(x):             
        return 1-(1/6)*x**2
def Q(z):
         return S(0)/S(z)
x=[x0-xe+(i/n)*(xg-x0) for i in np.arange(0,n,1)]
def lamda(z):
         m=round(Q(z),2)
         if z>= 0:                 
                  x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,1.5)
                  return x[0]
         if z<0:
                  x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,0.5)
                  return x[0]
plt.title('Газодинамическая функция температуры')
t0=293
y=[ t0*tau(lamda(z)) for z in x]
stop = time.time()
print (" Время работы программы:",round(stop-start,3))
plt.ylabel('T(xi)-температура газового потока град. С' )
plt.xlabel('xi -координата вдоль оси сопла')  
plt.plot(x,y,'r')
plt.grid(True)
plt.show()

Время работы программы: 0.203

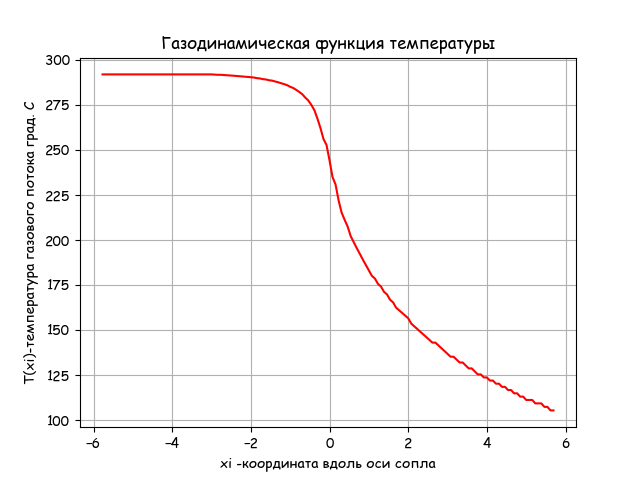
sa26tpmfwt-easharmil0nq25sq.png

Вывод
Температура на выходе из сопла уменьшается по приведенному в листинге уравнению газодинамики. Время выполнения программы приемлемое -0.203.

Испытательная установка:

id5zkgfjo6py8dmu4p899lfv4eq.png

Листинг для вычисления газодинамической функции давления
#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
import numpy as np
from math import *
from scipy.optimize import *
import time
start = time.time()
alfa=21.0#Угол сужения
beta=11.5#Угол расширения
rkr=1.1#Радиус критического сечения
R0=2*rkr
r1=0.5*rkr#Радиус округления сужающейся части сопла
r2=0.8*rkr#Радиус округления расширяющейся части сопла
ye=rkr+r2
L=1.2*R0#Длина прямого участка сопла Лаваля
x0=0
y0=R0
xa=L
ya=y0
xc1=xa
yc1=ya-r1
xc=xa+r1*cos(radians(90-alfa))
yc=yc1+r1*sin(radians(90-alfa))
yd=ye-r2*sin(radians(90-alfa))
xd=xc+(yc-yd)/tan(radians(alfa))
xc2=xd+r2*sin(radians(alfa))
xe=xc2
xf=xe+r2*cos(radians(90-beta))
yf=ye-r2*sin(radians(90-beta))
def R(x):     
        if x0<=x<=xa:
               return ya*1e-4
        if xa<=x<=xc:
               return (yc1+sqrt(r1**2-(x-xc1)**2))*1e-4
        if xc<=x<=xd:
               return (-tan(radians(alfa))*(x-xc)+yc)*1e-4
        if xd<=x<=xf:
                return (ye-sqrt(r2**2-(x-xe)**2))*1e-4
        if xf<=x:
                return (yf+tan(radians(beta))*(x-xf))*1e-4
def S(x):
         return pi*R(x+xe)**2
xg=2*xe
n=150
RG=287 #Газовая постоянная  
Tt=611 #Температура торможения
k=1.4
def tau(x):      
        return 1-(1/6)*x**2
def eps(x):       
        return (1-(1/6)*x**2)**2.5
def pip(x):             
        return 1-(1/6)*x**2
def Q(z):
         return S(0)/S(z)
x=[x0-xe+(i/n)*(xg-x0) for i in np.arange(0,n,1)]
def lamda(z):
         m=round(Q(z),2)
         if z>= 0:                 
                  x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,1.5)
                  return x[0]
         if z<0:
                  x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,0.5)
                  return x[0]
plt.title('Газодинамическая функция давления')
p0=3.6
y=[ 3.6*pip(lamda(z)) for z in x]
stop = time.time()
print ("Время работы программы:",round(stop-start,3))
plt.ylabel('P(xi)-давление газового потока в МПа' )
plt.xlabel('xi -координата вдоль оси сопла')  
plt.plot(x,y,'r')
plt.grid(True)
plt.show()

Время работы программы: 0.203

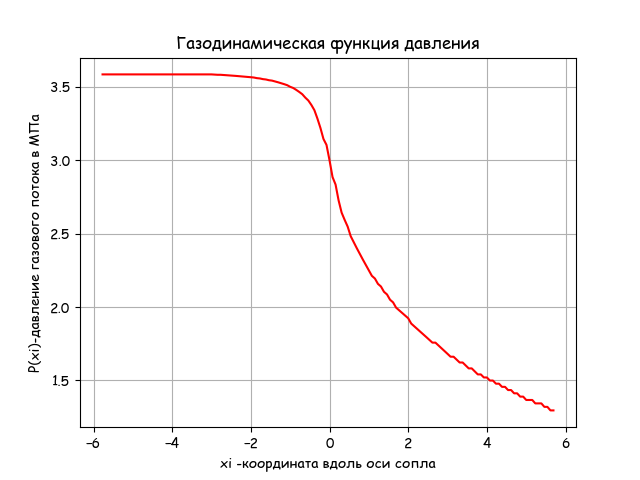
vtqfji_ihsmjcwksrzkqjjulgq0.png

Вывод

Давление на выходе из сопла уменьшается по приведенному в листинге уравнению газодинамики. Время выполнения программы приемлемое -0.203.

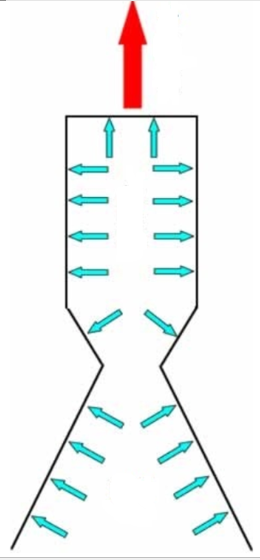
Возникновение силы тяги от действия давления газа схематично показано на рисунке:

esunynnvfk7ll99v_wxbguvykkq.png

Листинг для вычисления газодинамической функции относительной плотности газа
#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
import numpy as np
from math import *
from scipy.optimize import *
import time
start = time.time()
alfa=21.0#Угол сужения
beta=11.5#Угол расширения
rkr=1.1#Радиус критического сечения
R0=2*rkr
r1=0.5*rkr#Радиус округления сужающейся части сопла
r2=0.8*rkr#Радиус округления расширяющейся части сопла
ye=rkr+r2
L=1.2*R0#Длина прямого участка сопла Лаваля
x0=0
y0=R0
xa=L
ya=y0
xc1=xa
yc1=ya-r1
xc=xa+r1*cos(radians(90-alfa))
yc=yc1+r1*sin(radians(90-alfa))
yd=ye-r2*sin(radians(90-alfa))
xd=xc+(yc-yd)/tan(radians(alfa))
xc2=xd+r2*sin(radians(alfa))
xe=xc2
xf=xe+r2*cos(radians(90-beta))
yf=ye-r2*sin(radians(90-beta))
def R(x):     
        if x0<=x<=xa:
               return ya*1e-4
        if xa<=x<=xc:
               return (yc1+sqrt(r1**2-(x-xc1)**2))*1e-4
        if xc<=x<=xd:
               return (-tan(radians(alfa))*(x-xc)+yc)*1e-4
        if xd<=x<=xf:
                return (ye-sqrt(r2**2-(x-xe)**2))*1e-4
        if xf<=x:
                return (yf+tan(radians(beta))*(x-xf))*1e-4
def S(x):
         return pi*R(x+xe)**2
xg=2*xe
n=150
RG=287 #Газовая постоянная  
Tt=611 #Температура торможения
k=1.4
def tau(x):      
        return 1-(1/6)*x**2
def eps(x):       
        return (1-(1/6)*x**2)**2.5
def pip(x):             
        return 1-(1/6)*x**2
def Q(z):
         return S(0)/S(z)
x=[x0-xe+(i/n)*(xg-x0) for i in np.arange(0,n,1)]
def lamda(z):
         m=round(Q(z),2)
         if z>= 0:                 
                  x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,1.5)
                  return x[0]
         if z<0:
                  x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,0.5)
                  return x[0]
plt.title('Газодинамическая функция относительной плотности газа')
y=[ eps(lamda(z)) for z in x]
stop = time.time()
print ("Время работы программы:",round(stop-start,3))
plt.ylabel('Относительная плотность' )
plt.xlabel('xi -координата вдоль оси сопла')  
plt.plot(x,y,'r')
plt.grid(True)
plt.show()

Время работы программы: 0.203

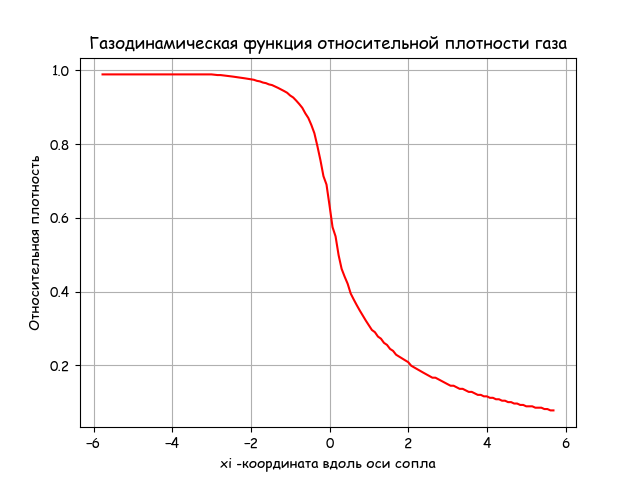
w3jcg5r6a3itughf2b6t4fl8w94.png

Вывод

Плотность газа на выходе из сопла уменьшается по приведенному в листинге уравнению газодинамики. Время выполнения программы приемлемое.

Выводы


1. Разработан метод решения средствами Python вещественных корней нелинейных степенных уравнений с дробными показателями степени используемых для описания газодинамических процессов. Метод основан на применении решателя fsolve из модуля scipy. optimize.

2. С помощью разработанного метода, решена демонстрационная задача расчёта сопла современных ракетных двигателей с определением следующих газодинамических функций: скорости; температуры; давления; плотности реактивных газов.

Ссылки


1. А.А. Дорофеев Основы теории тепловых ракетных двигателей (Общая теория ракетных двигателей) МГТУ им. Н.Э. Баумана Москва 1999 г.
2. Ландау Л. Д., Лифшиц Е.М. Глава X. Одномерное движение сжимаемого газа. § 97. Истечение газа через сопло // Теоретическая физика. — Т. 6. Гидродинамика.

© Habrahabr.ru