Две геометрические задачки, которые попадались на собеседовании, и где они обитают
Когда программист ходит на собеседования, то рано или поздно сталкивается с математическими задачками. В этом посте я рассмотрю две геометрические задачи и их решения.
Задача №1.
Первая задача довольно проста и звучит так:
Есть прямоугольник, в нем вырезали кружок, сколько прямых можно провести,
которые разделят на равновеликие части получившуюся фигуру.
Равновеликие фигуры — это фигуры, которые имеют одинаковые площади. Помним, что круг делится пополам в случае прохождения прямой через его центр. Прямоугольник делится пополам линиями, проходящими через его центр пересечения диагоналей. Ну и капитан очевидность нам подсказывает, что мы получим равновеликие части фигуры, если проведем прямую через центры прямоугольной фигуры и вырезанной круглой части. Такая прямая одна, если центры прямоугольника и круга не совпадают. В случае совпадения центров фигур, количество прямых будет бесконечное множество. Сделано.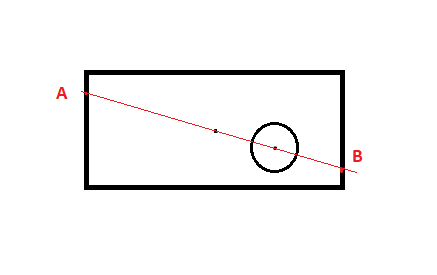
Задача №2.
Вторая задача чуть посложнее, поскольку вариантов перебора больше. Итак, условие:
Сколько можно провести плоскостей, равноудаленных от четырех точек в 3-х мерном пространстве. Эти точки не лежат в одной плоскости.
Если еще раз внимательно прочитать условие, то можно обратить внимание на то, что четыре точки не лежат на одной плоскости. Эта информация сокращает количество возможных расположений точек, удовлетворяющих условию равноудаленности от искомой плоскости:
1) три точки лежат по одну сторону от рассматриваемой плоскости, четвертая — по другую;
2) по каждую сторону от плоскости лежат по две точки.
Рассматривая первый случай, сразу же исключается возможность расположения трех точек на одной прямой, поскольку тогда через эти три точки и четвертую можно будет провести плоскость, а это противоречит условию задачи. Итак, искомая плоскость должна быть равноудалена от трех выбранных точек (например, A, B и C), а значит она должна быть параллельна плоскости ABC, проведенной через эти точки. Но искомая плоскость также должна быть равноудалена от точки D, поэтому проводим плоскость, параллельную плоскости ABC через середину перпендикуляра DP, опущенного из точки D на плоскость ABC.

Относительно четырех точек получим четыре искомые плоскости, равноудаленные от этих точек и такие, что по одну сторону от них расположена только одна точка, а по другую — оставшиеся три.
Приступим к рассмотрению второго случая.
Пусть точки A и B лежат по одну сторону от искомой плоскости, а точки C и D — по другую. Так как искомая плоскость равноудалена от точек A и B, то она должна быть параллельна прямой AB. И поскольку эта плоскость равноудалена от точек C и D, то она должна быть параллельна прямой CD. Точки A, B, C и D не лежат в одной плоскости, то прямые AB и CD — скрещивающиеся.
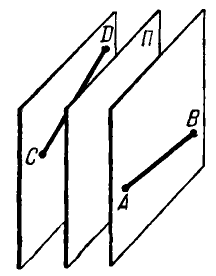
Проведем через эти скрещивающиеся прямые параллельные плоскости. Чтобы искомая плоскость была равноудалена от рассматриваемых точек, она должна быть параллельна построенным через скрещивающиеся прямые плоскостям и проходить ровно посередине между этими плоскостями. И для каждого такого рассматриваемого случая искомая плоскость будет единственной.
Таким образом, существуют три плоскости, равноудаленные от данных четырех точек и такие, что по одну сторону находятся две из четырех точек, а по вторую сторону — остальные две (AB и CD, AC и BD, AD и BC).
Итак, получаем общее число плоскостей, равноудаленных от данных четырех точек, равно семи (четыре при рассмотрении первого случая и три — второго случая). Вторая задача решена.
Каково было мое удивление, когда через полтора месяца, как мне попалась эта задача, я наткнулась в интернете на книжку «Неэлементарные задачи в элементарном изложении» А.М. Яглом и И.М. Яглом 1954 года издания, которая содержит школьные олимпиадные задачи.

Задача про плоскости в этом сборнике идет под номером один. Так что кому интересно, могут ознакомиться с другими задачами и решениями.
Вот так всегда: учишься в школе, поступаешь в институт, а в институте говорят «забудь, что учил в школе», затем идешь работать и слышишь «забудь, чему тебя учили в институте», потом идешь на какое-то собеседование, а тебе дают задачку из школьных олимпиад =) Как ни крути, а знания лишними не бывают.
