Прогнозирование продаж Python. Как находить и сглаживать выбросы с помощью фильтра Хэмплея03.12.2022 12:02

Те, кто работает с временными рядами, часто сталкивается с двумя проблемами. Первая — нет полных данных. Вторая — битые данные, когда встречается много выбросов, шума и пропусков. Редко встречаются случаи, когда всё было бы идеально. И данных много, и можно легко найти нужные. Такое встретишь крайне редко или почти никогда.

Возникает вопрос — как решить эту проблему? Я нашёл решение. Давайте расскажу вам, как я решаю проблему битых данных, выбросов, пропусков. Какие я использовал методы, в чем их отличия, преимущества и какие я считаю самыми лучшими.

Начнём мы с первого метода — фильтра Хэмплея. В этой статье речь пойдёт именно о нём. Я постараюсь как можно проще рассказать о его особенностях и показать всё на наглядных примерах. Приступим.

Как работает фильтр Хэмплея

Для начала стоит понять, что такое фильтр Хэмплея. В интернете о нём вы мало что найдёте. По крайней мере, я встретил лишь скудную информацию. Хотя потратил много времени на поиски нужной информации о фильтре.

Главная цель Хэмплея — найти и заменить выбросы в заданном временном ряду. Для этого в своей основе он использует скользящее среднее с заданным окном. Для каждой итерации или окна фильтр вычисляет медиану и стандартное отклонение. Оно выражается в среднем абсолютном значении и обозначается как MAD.

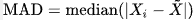Материал из вики: https://en.wikipedia.org/wiki/Median_absolute_deviation

Чтобы MAD стал последовательной оценкой стандартного отклонения надо умножить его на постоянный коэффициент k. Коэффициент зависит от распределения. Мы считаем, что данные подчиняются распределению Гаусса, поэтому берём коэффициент равным 1,4826.

Если значение медианы окна скользящего среднего больше чем х стандартных отклонений, то это — выброс.

Фильтр Хэмплея имеет 2 настраиваемых параметра:

·         размер раздвижного окна

·         количество стандартных отклонений, которые идентифицируют выброс

Для начала надо импортировать нужные библиотеки:

import matplotlib.pyplot as plt
import warnings
import pandas as pd
import numpy as np

Загрузить данные из csv файла:

df = pd.read_csv('data.csv')

Распечатать данные

df.head()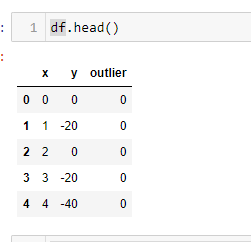

Вы можете заметить, что выбросы в df уже помечены. Это делается для того, чтобы мы могли сравнить работу алгоритма с фактом.

Далее визуализируем наш df

plt.plot(df.x, df.y)
plt.scatter(df[df.outlier == 1].x, df[df.outlier == 1].y, c='r', label='outlier')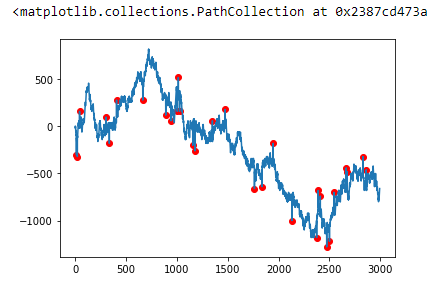

Теперь можно реализовывать фильтр Хэмпеля. Для этого используем 3 стандартных отклонения. Почему именно 3? Потому что этого с лихвой хватит для нашего временного ряда.

def hampel(y, window_size, simg=3):    
    n = len(y)
    new_y = y.copy()
    k = 1.4826
    idx = []

    for i in range((window_size),(n - window_size)):
        r_median = np.median(y[(i - window_size):(i + window_size)]) #скользящая медиана 
        r_mad  = np.median(np.abs(y[(i - window_size):(i + window_size)] - r_median)) #скользящий MAD 
        if (np.abs(y[i] - r_median) > simg * r_mad):
            new_y[i] = r_median #замена выброса
            idx.append(i)
    
    return new_y, idx

Вызываем фильтр Хэмплея с окном скользящего среднего равного 3, чтобы определить выброс. Этого будет достаточно для нашей задачи.

new_y, outliers = hampel(df.y, 3)

В переменной new_y лежит новый временный ряд без выбросов. В outliers — индексы выбросов во временном ряду.

Заливаем новый временный ряд в df вместе с признаками выбросов.

df['new_y'] = new_y
df.loc[outliers, 'outlier_hampel'] = 1

Осталось визуализировать данные.

from matplotlib.pyplot import figure
figure(figsize=(15, 6), dpi=80)
plt.plot(df.x, df.y)
plt.plot(df.x, df.new_y)
plt.scatter(df[df.outlier == 1].x, df[df.outlier == 1].y, c='r', label='outlier')
plt.scatter(df[df.outlier_hampel == 1].x, df[df.outlier_hampel == 1].y, c='b', label='outlier')

Выбросы, размеченные вручную, выделяются красным цветом. Синие выбросы — это определение модели.

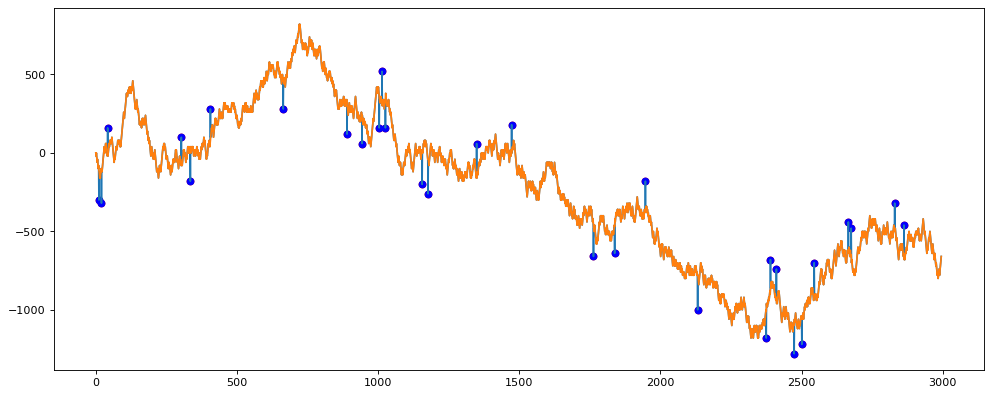
На графике видно, что красного цвета нет. Вывод — алгоритм работает на отлично.

Для лучшего понимания возьмём другой временной ряд, чтобы снова проверить алгоритм.

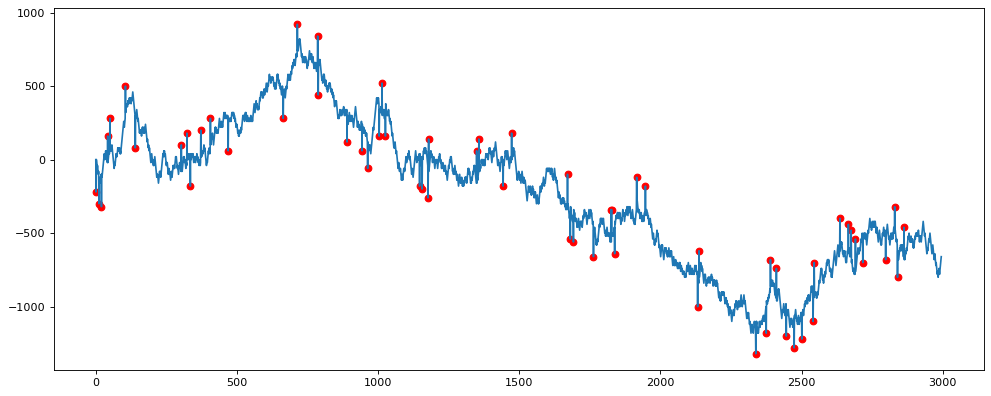
Здесь заметим, что выбросов гораздо больше.

new_y, outliers = hampel(df_new.y, 3)
df_new['new_y'] = res
df_new.loc[detected_outliers, 'outlier_hampel'] = 1

from matplotlib.pyplot import figure
figure(figsize=(15, 6), dpi=80)
plt.plot(df_new.x, df_new.y)
plt.plot(df_new.x, df_new.new_y)
plt.scatter(df_new[df_new.outlier == 1].x, df_new[df_new.outlier == 1].y, c='r', label='outlier')
plt.scatter(df_new[df_new.outlier_hampel == 1].x, df_new[df_new.outlier_hampel == 1].y, c='b', label='outlier')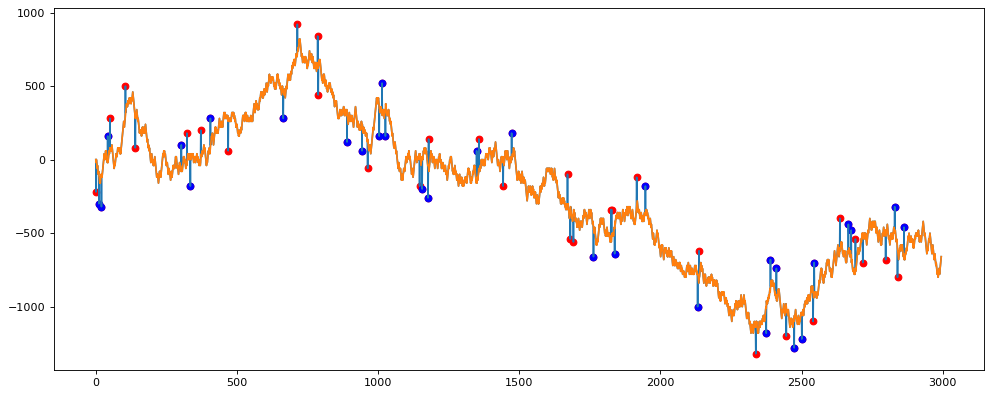

Увеличим окно скользящего среднего.

new_y, outliers = hampel(df_new.y, 5)
df_new['new_y'] = res
df_new.loc[detected_outliers, 'outlier_hampel'] = 1

from matplotlib.pyplot import figure
figure(figsize=(15, 6), dpi=80)
plt.plot(df_new.x, df_new.y)
plt.plot(df_new.x, df_new.new_y)
plt.scatter(df_new[df_new.outlier == 1].x, df_new[df_new.outlier == 1].y, c='r', label='outlier')
plt.scatter(df_new[df_new.outlier_hampel == 1].x, df_new[df_new.outlier_hampel == 1].y, c='b', label='outlier')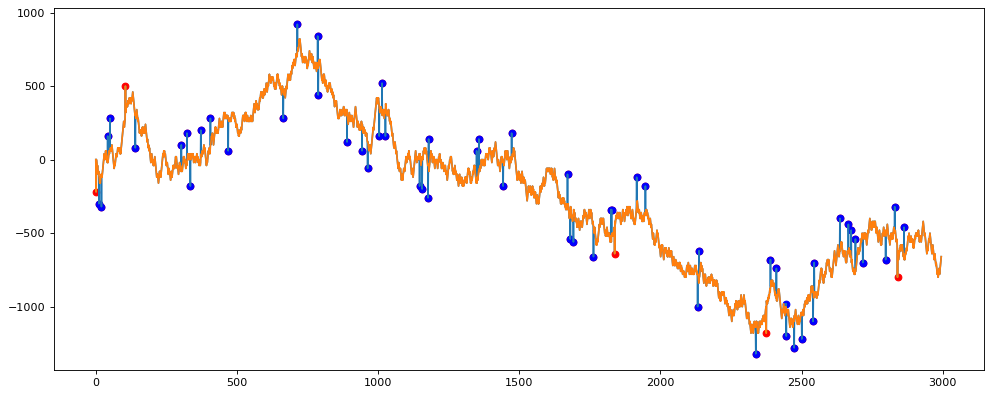

Видно, что стало гораздо лучше.

Что касается точности, то она равна 93.33333333333333%. Я считаю, что это отличный процент.

 (df_new[df_new.outlier_hampel == 1].shape[0]/df_new[df_new.outlier == 1].shape[0])*100

Что в итоге?

Фильтр Хэмпеля прекрасно справляется со своей задачей. Его главным преимуществом стала простота реализации. Он может работать быстро как на малых, так и на больших объемах данных. Само собой, есть что улучшить, но в качестве простого и рабочего инструмента фильтр Хэмпеля показывает себя весьма неплохо.

Но так ли он хорош, если сравнивать его с другими алгоритмами? Например, с тестом Греббса, критерием выбора Рознера и рандомным лесом. Об этом я расскажу в следующих статьях, а в конце сравним результаты работы каждого алгоритма и вынесем окончательный вердикт, что же лучше.

© Habrahabr.ru