Повышение точности решения плохо обусловленных СЛАУ методом Гаусса13.05.2023 12:46

Большинство задач вычислительной математики в конечном итоге сводятся к решению систем линейных уравнений. На данный момент существует огромное количество алгоритмов для решения таких систем. Их разделяют на две большие группы: итерационные и прямые. Прямые методы позволяют получить точные значения неизвестных, если вычисления проводятся точно. Далее будем рассматривать метод Гаусса. Этот метод можно использовать для решения систем алгебраических уравнений с так называемыми матрицами общего вида. Одновременно он позволяет определить —совместна ли система и, если она совместна — единственно ли решение? Однако, для всех методов есть проблема, связанная с трудностями плохо обусловленных систем. Это наиболее распространенный способ решения СЛАУ, в основе которого лежит идея последовательного исключения неизвестных (более подробно данный метод будет описан далее).

Алгоритм

Алгоритм метода использует последовательное исключение неизвестных. С помощью элементарных преобразований система уравнений в случае существования единственного решения приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все искомые неизвестные.

Алгоритм решения СЛАУ методом Гаусса состоит из двух этапов

На первом этапе, который принято называть прямым ходом, путём элементарных преобразований над уравнениями системы ее приводят к ступенчатой или верхнетреугольной форме. Алгоритм прямого хода с частичным выбором ведущего элемента в столбце предполагает, что в начале среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец, содержащий первую компоненту вектора неизвестных под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают, и продолжают аналогичные действия, пока не получится система с верхней треугольной матрицей.

На втором этапе, который называется обратным ходом, осуществляется последовательное определение компонент вектора неизвестных, начиная с последней. Число операций, необходимое для реализации прямого хода в методе Гаусса, можно рассчитать по формуле:

Q_1=2/3 n^3+n^2/2-n/6

В процессе реализации обратного хода алгоритм выполняет Q2 операций:

В работе исследуется влияние обусловленности СЛАУ на погрешность получаемого решения, в том числе для систем с матрицей Гильберта.

Программная реализация

Программа, реализующая алгоритм Гаусса на языке Python, приведена ниже.

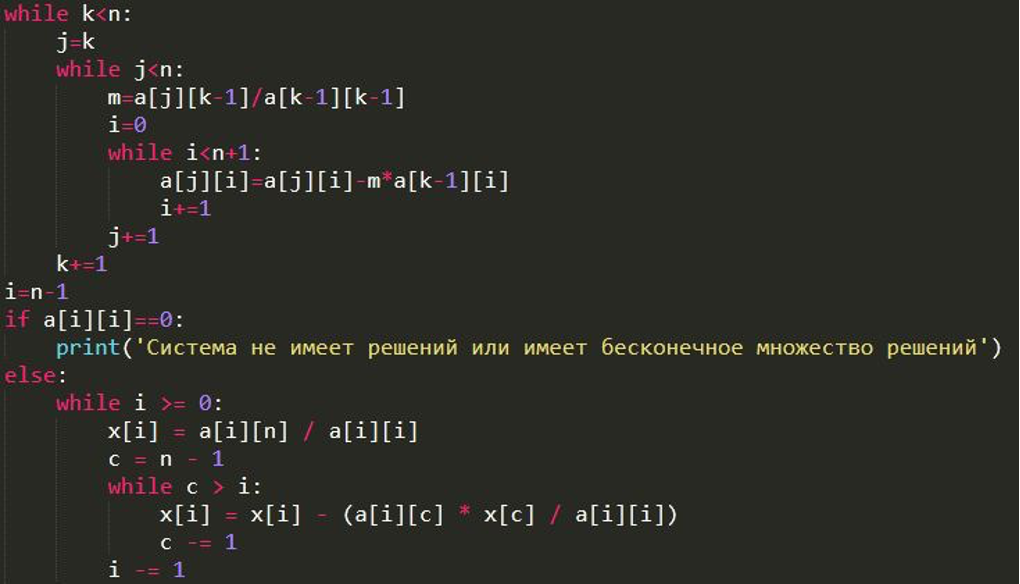
Для удобства ввода матрицы системы и неизвестных членов применен метод split ()

Данный метод позволяет вводить коэффициенты уравнения и свободный член через пробел. Для ввода следующего уравнения требуется нажатие клавиши ENTER.
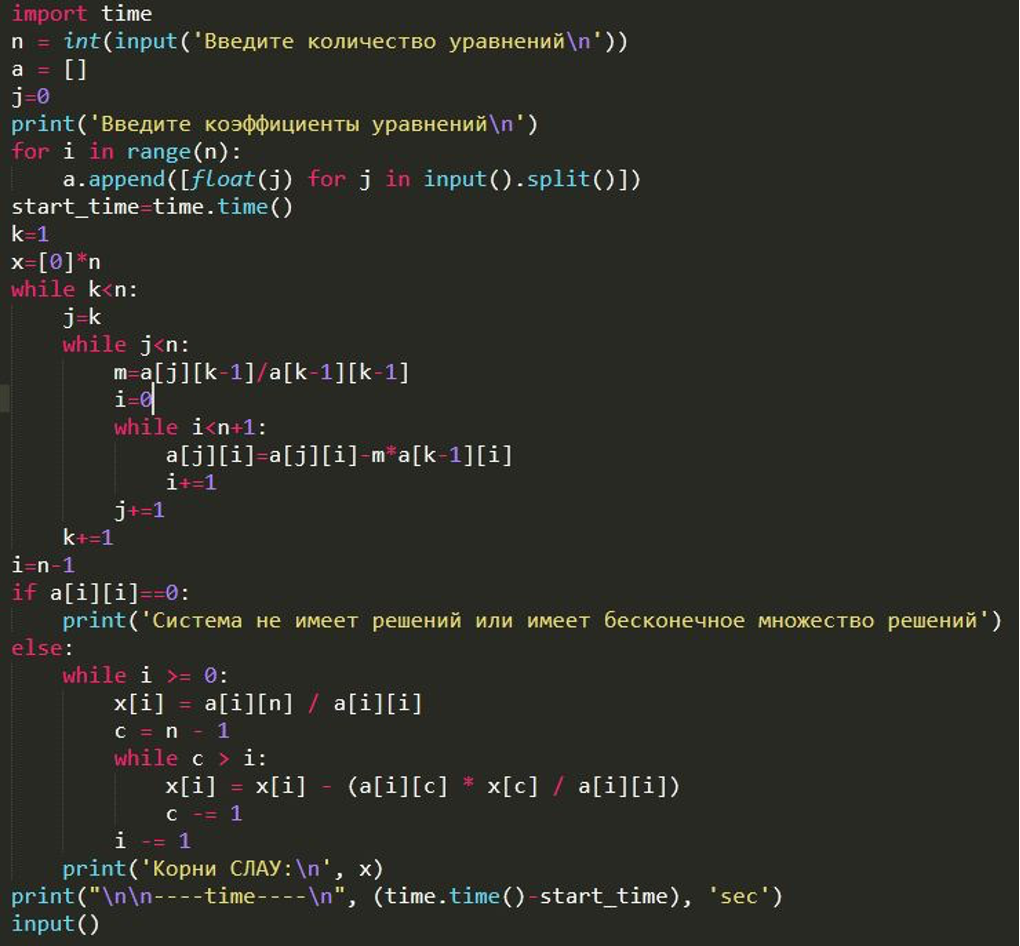
Полный текст программы с вводом и выводом информации выглядит следующим образом:

Тестирование программы

Для проверки работоспособности программы был проведен ряд тестов решения различных СЛАУ.

Первый тест

Второй тест

Третий тест

Также были проведены тесты и с плохо обусловленными системами. Для них мы взяли матрицу Гильберта размерами n×n как матрицу коэффициентов. Матрица Гильберта — квадратная матрица A с элементами

A_ij=1/(i+j-1);i,j=1,2,3,… ,n

СЛАУ с данной матрицей является хорошим примером плохо обусловленной системы, так как число обусловленности для 5 порядка у же равно μ (A)= 4.8×105
Число обусловленности матрицы показывает, насколько матрица близка к матрице неполного ранга (для квадратных матриц — к вырожденности). Т.е. если A почти вырожденная, то можно ожидать, что малые изменения в A и b вызовут очень большие изменения в x. Число обусловленности можно найти по следующим формулам:

$cond(A)≡‖A‖*‖A^{-1}‖$

где A-1— матрица, обратная для невырожденной матрицы A, ‖A‖, ‖A-1‖ — нормы матриц A и A-1 размерами n×n соответственно. Каждую из норм можно рассчитать по формуле:

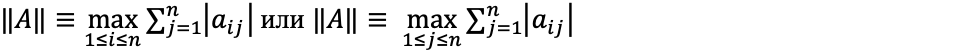
Если cond (A)≥103, то матрицу можно считать плохообусловленной.

Тест 4. СЛАУ с матрицей Гильберта Н. Пусть вектор b = (b1, b2, b3, … , bn)T выполняется в предположении уже известного вектора x =(1, 2, 3, …, n)T по формуле:

$b_i=∑_{k=1}^nh_{ik} x_k$

В итоге система принимает вид: Hx = b

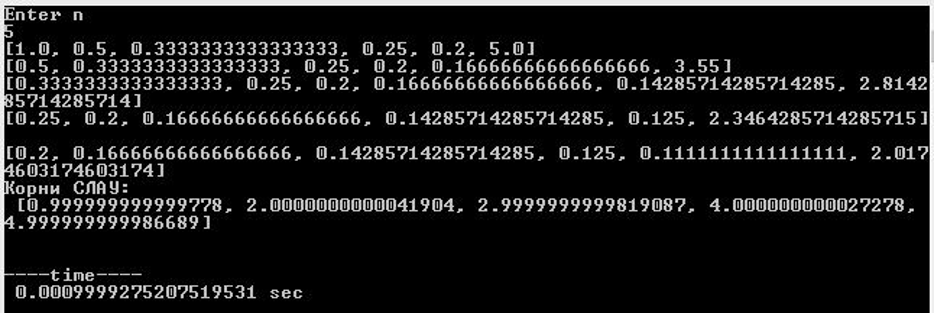
Матрица 5 порядка

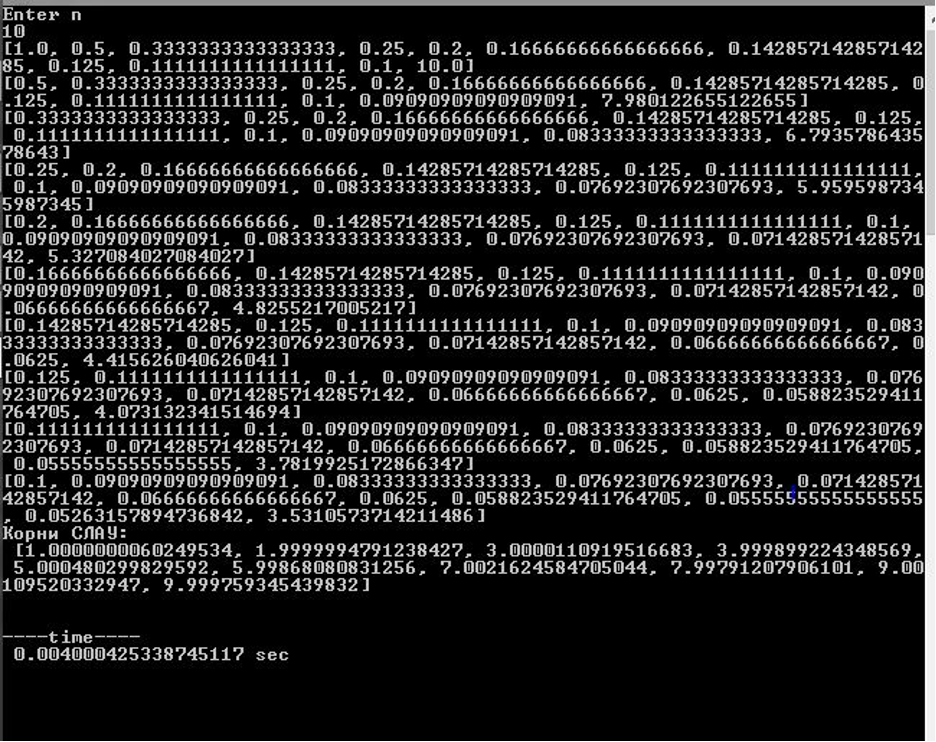
Матрица 10 порядка

Матрица 20 порядка

Как видно из результатов, погрешность в вычислениях уже заметна при n = 5. Критическую разницу между приближенным и точным решением можно наблюдать уже при n = 10. Cвязано это с приближенным представлением чисел в форме с плавающей точкой в компьютере в условиях плохой обусловленности матрицы Гильберта. Для того, чтобы исключить возмущения входных и промежуточных данных, вызванных ошибками округления воспользуемся библиотекой Fractions, которая позволяет представлять данные, в том числе результаты вычислений в виде числовых алгебраических дробей

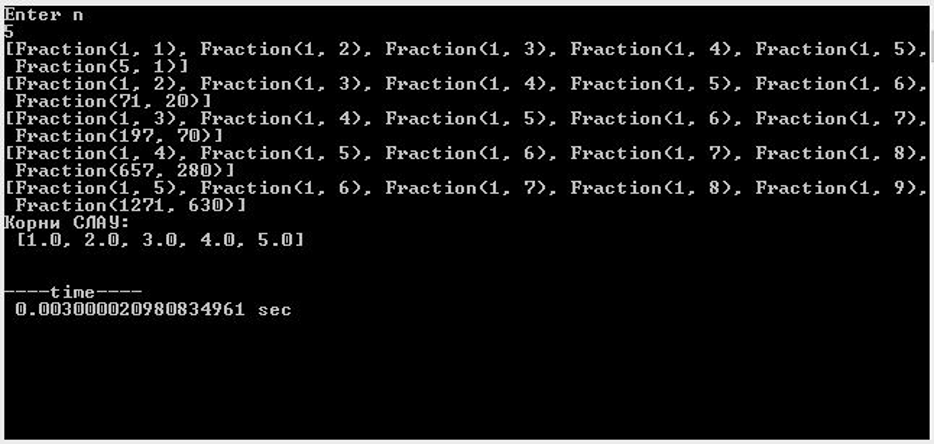
Матрица 5-го порядка и Fractions

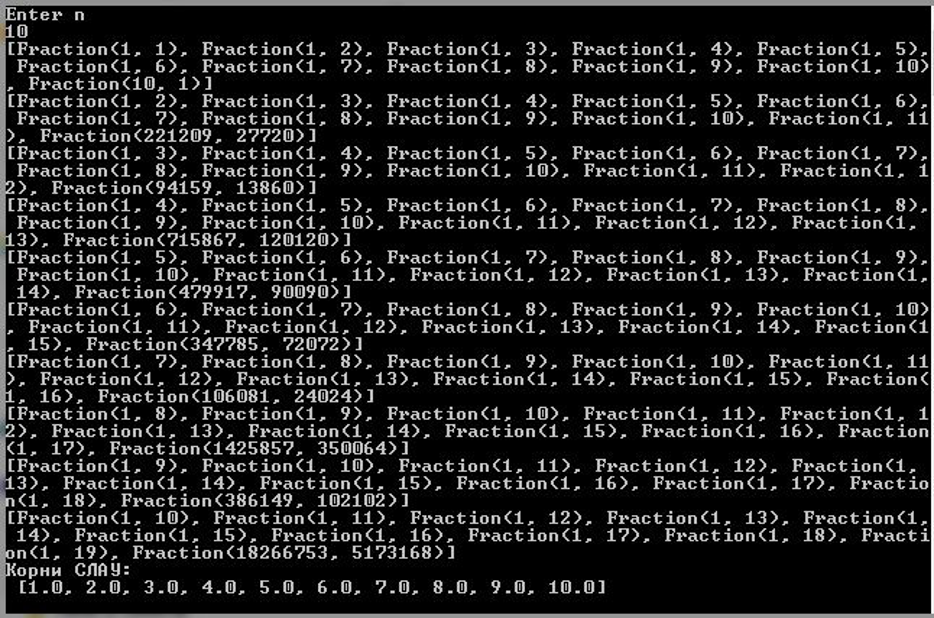
Матрица 10-го порядка и Fractions

Матрица 20-го порядка и Fractions

Как можно заметить, решения, полученные в результате вычислений с помощью библиотеки Fraction, совпадают с их «точным» представлением в виде вектора x = (1, 2, 3, … , n)T.

Все числа до момента получения окончательного результата представляются в виде пары чисел (числитель и знаменатель). Естественно, время, необходимое для вычисления решения, существенно возрастает, так как программа тратит большое количество времени для нахождения общего знаменателя при сложении двух дробей. Ниже приведена зависимость времени решения системы от порядка СЛАУ. Синим цветом изображено время работы с использование метода Fractions, а красным — с использованием стандартного типа данных float в котором и происходят все вычисления. На вертикальной оси — время в секундах, на горизонтальной — порядок матрицы Гильберта.

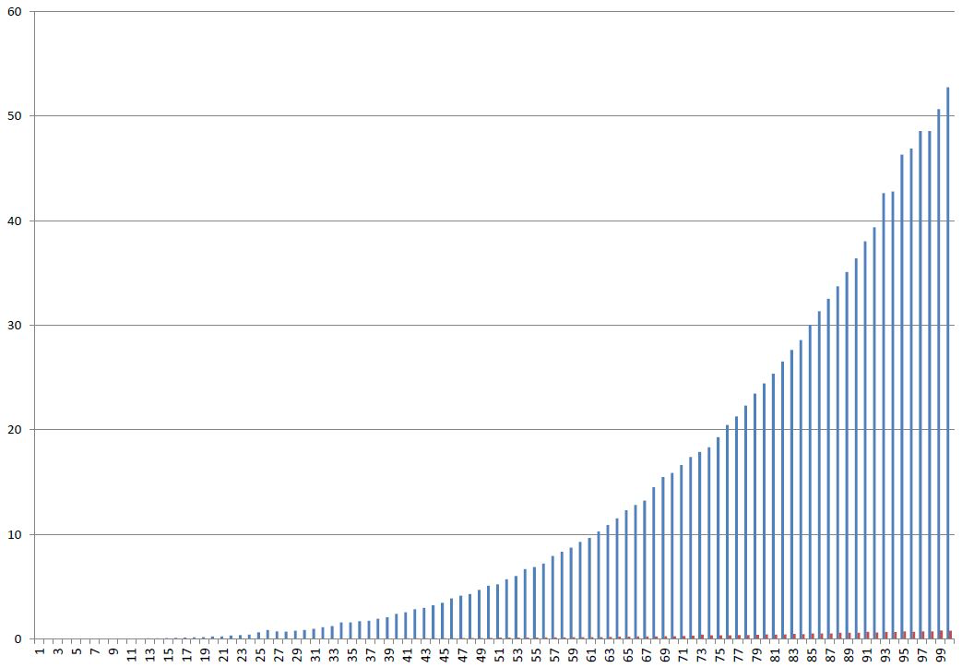
Время решения от порядка

Подводим итог

При решении СЛАУ важным является учет обусловленности матрицы системы. В случае большого значения числа обусловленности следует учитывать возможность существенного, а иногда и катастрофического влияния погрешностей округления и задания входных данных на получаемый результат (решение). В этом случае для исключения влияния погрешностей округления можно применять представление чисел в виде числовых алгебраических дробей. При этом время решения задачи может вырасти для систем порядка n, n>100 во многие десятки раз.