ИИ в спортивном программировании: обзор и перспективы

AlphaCode, который (частично) смог
Могут ли существующие модели успешно участвовать в соревнованиях по программированию? Обзор текущего состояния и много ссылок в тексте для заинтересовавшихся.
Общая информация
Будем говорить о классических соревнованиях по спортивному программированию: небольшая продолжительность, формально поставленные задачи с ограничениями на время работы и доступную память, автоматическая проверка на закрытом наборе тестов. Конечно, популярные offline-соревнования такого формата (например, ICPC и IOI) не дают официальной возможности для участия ИИ. Поэтому в качестве метрики успешности проще всего взять результаты на популярной online-платформе, то есть Codeforces. Именно это и сделали авторы двух наиболее успешных и известных моделей: AlphaCode и ChatGPT.
AlphaCode
Вероятно, самый успешный (и определённо лучше всего задокументированный) эксперимент по участию ИИ в соревнованиях провели в начале 2022 года Codeforces и Google DeepMind (известный по AlphaGo и AlphaZero). Модель AlphaCode получала тексты задач нескольких раундов и делала самостоятельные посылки решений под тестовыми аккаунтами. Тексты всех посылок доступны, профили участников — SelectorUnlimited, WaggleCollide и AngularNumeric. Участие было нерейтинговым, но если бы рейтинг начислялся, он оказался бы равен примерно 1300 (близко к среднему рейтингу Codeforces). Уровень очень далёк от мировых чемпионов (с рейтингом более 3000), и даже не входит в первый дивизион (от 1900). Но, тем не менее, ИИ с таким рейтингом был бы впереди почти половины участников-людей. AlphaCode более-менее успешно решал задачи уровня A и B, частично — уровня C дивизиона 2.
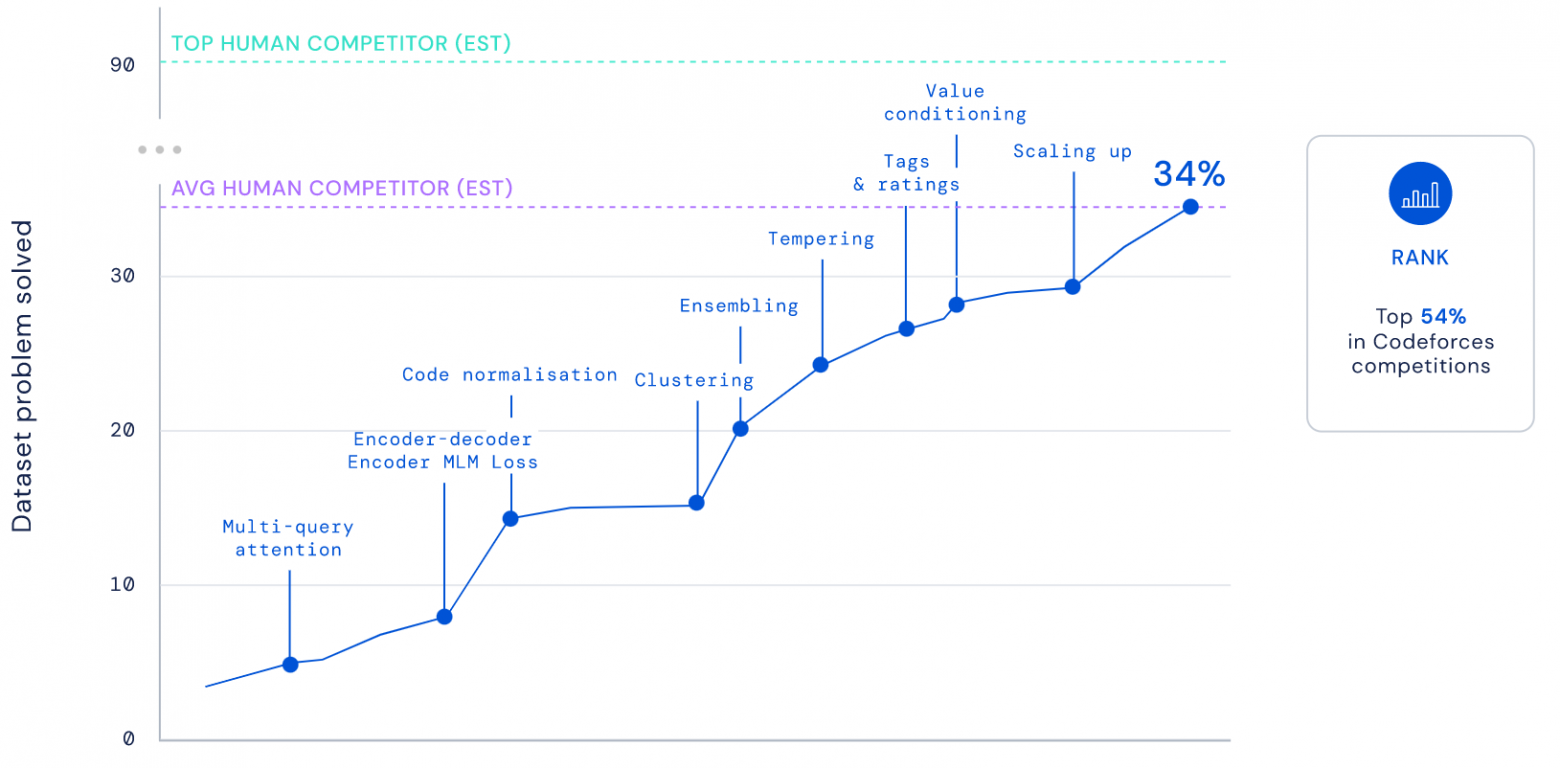
Все любят растущие графики
Самое важное: модель AlphaCode — это не модель общего назначения, и даже не модель для написания произвольного программного кода. Она создавалась специально для участия в соревнованиях. Предварительно натренированная на данных GitHub (~715 Гб), модель прошла обучение на данных CodeContests (~2.6 Гб). Датасет доступен публично, в нём содержатся данные о задачах и решениях на платформах Codeforces, CodeChef, AtCoder и некоторых других (всего более 10 тысяч задач, в среднем почти 1000 решений для каждой). В эксперименте участвовали модели объёмом 41 млрд и 9 млрд параметров, обучение (по заявлению DeepMind) потребовало 2149 петафлоп/c-дней.
В процессе тестирования для каждой задачи генерировалось несколько решений-кандидатов, при неудаче первой посылки производилась следующая, и так далее, до 10 попыток на задачу. Это увеличило вычислительные затраты, но существенно улучшило результат. Только 66% решённых задач были сданы с первой попытки.
После официального пресс-релиза в феврале 2022 была дополнительно опубликована небольшая демонстрация работы AlphaCode (с комментариями Петра Митричева, частично вынесенными на КДПВ). А в конце 2022 — соответствующая статья в Science — довольно подробная, но не содержащая никакой информации о каких-либо более поздних экспериментах.
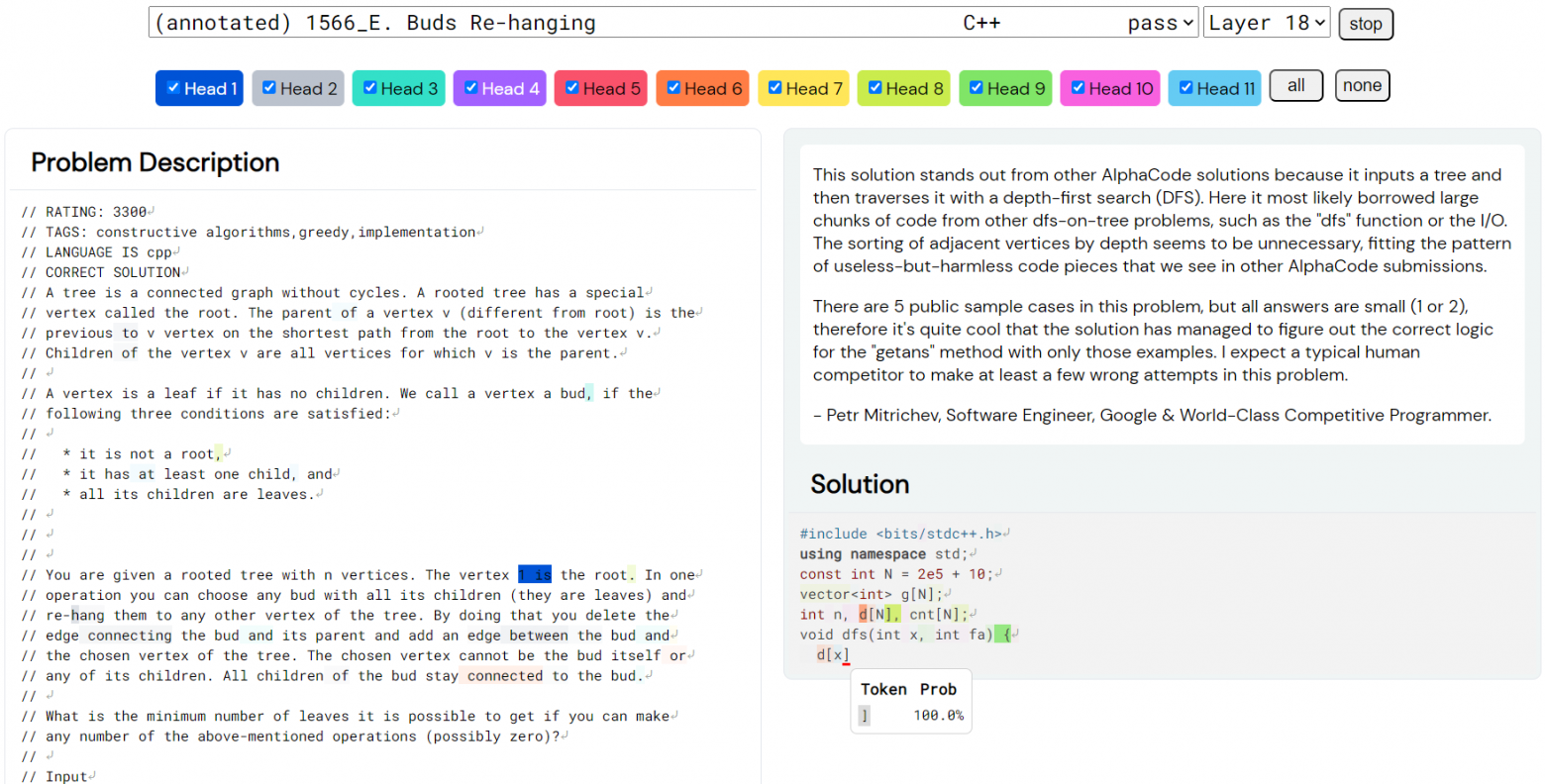
Демо AlphaCode: много разноцветной анимации и комментарии Петра Митричева
Каковы же итоги и перспективы? Эксперимент проводился почти полтора года назад, и с тех пор прошла целая вечность по меркам этого направления. Судя по всему, доступ к AlphaCode так и не был предоставлен никому за пределами Google DeepMind. Более новых публикаций про AlphaCode найти не удалось, а команда DeepMind, вероятно, сфокусирована на работе над LaMDA и Bard. Учитывая это, а так же недавнюю отмену Google Code Jam — кажется, спортивное программирование в Google отодвинуто на задний план и ожидать каких-то существенных обновлений в ближайшее время не стоит. AlphaCode удалось показать очень неплохие результаты, но даже близко не удалось повторить успех AlphaGo и AlphaZero.
ChatGPT
Из более новых моделей — что же умеет легендарный ChatGPT? По заявлению самих OpenAI, GPT 3.5 имеет Codeforces рейтинг 260, а GPT 4.0 — рейтинг 392. Как он определялся? Информации здесь гораздо меньше, чем по AlphaCode, но краткое описание можно найти в недавней публикации. Примерный перевод:
A.6 Codeforces rating
Чтобы определить рейтинг Codeforces (рейтинг Эло), мы оценили каждую из моделей на 10 недавних контестах. Каждый контест включал около 6 задач, и модели было дано по 10 попыток на задачу. После каждого контеста мы пересчитывали рейтинг Эло на основе результата модели до тех пор, пока он не сходился к равновесному значению (это моделировало многократное участие в контестах с одинаковым результатом). Мы моделировали каждый из 10 контестов по 100 раз, и вычислили средний равновесный рейтинг Эло среди всех контестов. Около 50% симуляций включали 0 решенных задач, что приводило к рейтингу 0. В результате, итоговый рейтинг оказался довольно низким. Максимальный равновесный рейтинг, достигнутый в отдельном контесте, был около 1000 для GPT-3.5 и 1300 для GPT-4.
Авторы явно ориентировались на метод тестирования AlphaCode (10 контестов, 10 попыток на задачу, вычисление среднего результата по каждому из контестов). Но результат отличается разительно — фактически, итоговый рейтинг действительно слабо отличим от 0. Почему так получается, и неужели всё так плохо? К сожалению, тестовые посылки не были официально опубликованы. Но к счастью, ChatGPT более-менее публично доступна (в отличие от абсолютно закрытой AlphaCode), поэтому аналогичные эксперименты можно в каком-то объеме повторить самостоятельно.
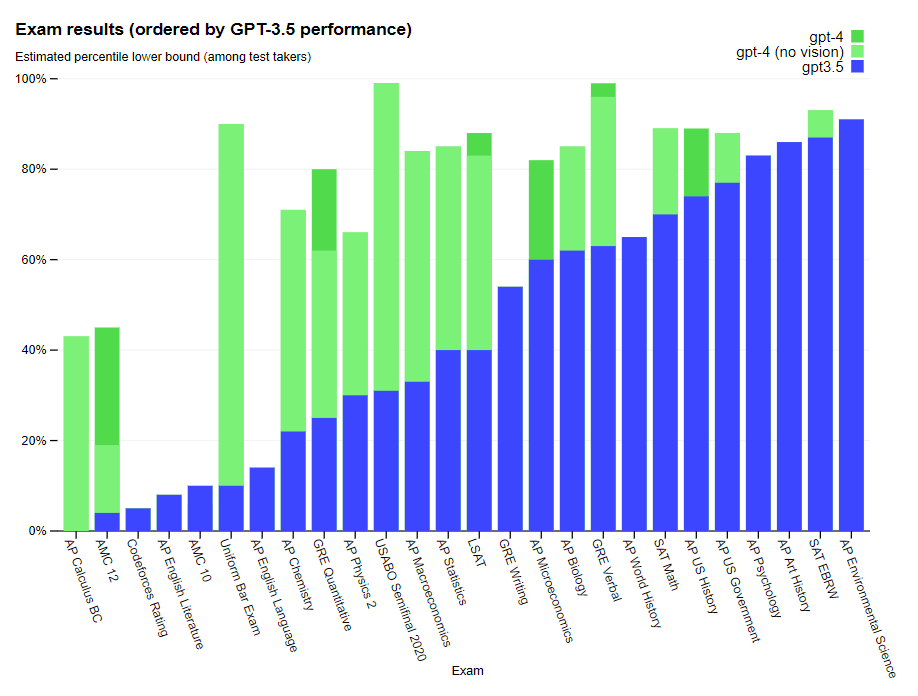
Видите третий слева маааленький столбик? Он-то нам и нужен
Выберем несколько задач разной сложности на разные темы и попробуем решить их с помощью ChatGPT (похожий эксперимент уже проводил @bekishev04 в недавней статье). Конечно, результат на малой выборке будет не слишком значим, но можно получить хотя бы определённое представление о том, что происходит. Пара интересных примеров приведены ниже.
Задача 1 (рейтинг 800 — минимальный). Полное решение.
Диалог
Реши задачу на языке Python. Решение должно быть эффективным.
Вам дано целое положительное число x. Найдите любые такие два 2 целые положительные числа a и b, для которых НОД (a, b)+НОК (a, b)=x. Напомним, что НОД (a, b) — это наибольшее целое число, на которое делятся и a и b. Аналогично, НОК (a, b) — это наименьшее целое число, которое делится и на a и на b. Гарантируется, что решение всегда существует. Если существует несколько таких пар (a, b), вы можете вывести любую из них.
Входные данные
Первая строка содержит одно целое число t (1≤t≤100) — количество наборов тестовых данных. Каждый набор тестовых данных состоит из одной строки, содержащей одно целое число, x (2≤x≤109).
Выходные данные
Для каждого набора тестовых данных, выведите пару целых положительных чисел a и b (1≤a, b≤109) таких, что НОД (a, b)+НОК (a, b)=x. Гарантируется, что решение всегда существует. Если существует несколько таких пар (a, b), вы можете вывести любую из них.
Одно из возможных решений задачи:
import math
t = int(input())
for i in range(t):
x = int(input())
a = 1
b = x - 1
while math.gcd(a, b) + (a * b) // math.gcd(a, b) != x:
a += 1
b = x - a
print(a, b)Алгоритм решения заключается в переборе всех возможных пар чисел (a, b) таких, что a + b = x, и проверке условия НОД (a, b)+НОК (a, b)=x для каждой пары. Перебор осуществляется сначала для a = 1, b = x — 1, затем увеличивая a на 1 и уменьшая b на 1 до тех пор, пока не будет найдена пара, удовлетворяющая условию.
Для проверки условия используются функции math.gcd () и оператор // для вычисления НОК (a, b) через НОД (a, b).
Такой подход гарантирует нахождение хотя бы одной пары (a, b) для любого заданного x. Однако, для больших значений x, время выполнения может быть значительным.
Мои комментарии
Формально, задача решена с первой же попытки. Но (в основном) это просто везение: как верно отмечает сама же модель в комментариях к коду, перебор миллиарда элементов требует слишком много времени. Поскольку НОД (1, X-1) + НОК (1, X-1) = 1 + (X-1) = X, то перебор вообще не требуется: первая же пара решений всегда подходит. К счастью для ChatGPT, именно эта пара решений и перебиралась первой.
Безусловно, «живые» участники иногда посылают решения без точной оценки их времени работы, имея лишь правдоподобные предположения. В каких-то случаях предположения оказываются верными и решение действительно проходит. Но здесь, как видим, случай другой — модель реализовала полное переборное решение без каких-либо предположений о том, почему перебор может завершаться раньше времени.
Задача 2 (рейтинг 1200 — простая техническая задача). Полное решение раз, полное решение два.
Диалог 1
Напиши программу для решения следующей задачи. Вы — университетский тренер. Всего в университете под Вашим надзором n студентов, умение программировать i-го студента равно ai. Вы хотите составить команду для нового соревнования по программированию. Как Вы знаете, чем больше студентов на соревновании — тем больше шансов победить! Поэтому Вы хотите составить максимальную по количеству студентов команду. Но Вы также знаете, что команда должна быть сбалансированной. Это означает, что умение программировать каждой пары студентов в команде должно отличаться не более, чем на 5. Ваша задача — найти максимально возможное количество студентов в сбалансированной команде. Первая строка входных данных содержит одно целое число n — количество студентов. Вторая строка входных данных содержит n целых чисел a1, a2, …, an, где ai означает умение i-го студента программировать. Выведите одно целое число — максимально возможное количество студентов в сбалансированной команде.
Конечно, вот решение данной задачи на Python:
n = int(input()) # количество студентов
a = list(map(int, input().split())) # список умений студентов
a.sort() # сортируем список
max_team_size = 1 # максимальный размер команды
curr_team_size = 1 # текущий размер команды
left = 0 # левая граница окна
right = 1 # правая граница окна
while right < n: # пока правая граница не достигнет конца списка
if a[right] - a[left] <= 5: # если умение программировать каждой пары студентов в команде отличается не более, чем на 5
curr_team_size += 1 # увеличиваем размер текущей команды
right += 1 # сдвигаем правую границу окна
else:
curr_team_size -= 1 # уменьшаем размер текущей команды
left += 1 # сдвигаем левую границу окна
max_team_size = max(max_team_size, curr_team_size) # обновляем максимальный размер команды
print(max_team_size) # выводим максимальный размер командыПример работы программы:
Входные данные:
7
1 3 4 7 10 11 12
Выходные данные:
4
Объяснение: Максимально возможная команда из семи студентов будет состоять из студентов с умениями программировать 3, 4, 7 и 10. Умение программировать каждой пары студентов в команде отличается не более, чем на 5.
Диалог 2
Напиши программу для решения следующей задачи.
Вы — университетский тренер. Всего в университете под Вашим надзором n студентов, умение программировать i-го студента равно ai. Вы хотите составить команду для нового соревнования по программированию. Как Вы знаете, чем больше студентов на соревновании — тем больше шансов победить! Поэтому Вы хотите составить максимальную по количеству студентов команду. Но Вы также знаете, что команда должна быть сбалансированной. Это означает, что умение программировать каждой пары студентов в команде должно отличаться не более, чем на 5. Ваша задача — найти максимально возможное количество студентов в сбалансированной команде. Первая строка входных данных содержит одно целое число n — количество студентов. Вторая строка входных данных содержит n целых чисел a1, a2, …, an, где ai означает умение i-го студента программировать. Выведите одно целое число — максимально возможное количество студентов в сбалансированной команде.
Вот решение задачи на языке Python:
n = int(input())
a = list(map(int, input().split()))
a.sort() # сортируем список
max_team_size = 0
for i in range(n):
team_size = 1
for j in range(i+1, n):
if a[j] - a[i] <= 5: # проверяем, сбалансирована ли команда
team_size += 1
if team_size > max_team_size:
max_team_size = team_size
print(max_team_size)Сначала мы считываем количество студентов n и список их умений a. Затем мы сортируем список a в порядке возрастания. Далее мы проходимся по всем возможным командам, начиная с каждого студента. Для каждой команды мы считаем количество студентов team_size, которые могут быть в ней, и проверяем, является ли команда сбалансированной. Если количество студентов в команде больше, чем максимальное количество студентов в командах, которые мы видели раньше, мы обновляем значение max_team_size. В конце мы выводим максимальное количество студентов в сбалансированной команде.
Какова временная сложность этого алгоритма?
Временная сложность этого алгоритма — O (n^2), где n — количество студентов. Это связано с тем, что мы проходимся по каждому студенту в списке и для каждого студента проходимся по оставшимся студентам, чтобы проверить, является ли команда сбалансированной. Это приводит к тому, что общее количество итераций составляет n*(n-1)/2, что дает нам временную сложность O (n^2). В худшем случае, когда все студенты имеют умение программировать, отличающееся не более, чем на 5, алгоритм будет работать медленно. Однако, если большинство студентов имеют умение программировать, отличающееся на большее расстояние, алгоритм будет работать быстрее.
Можешь придумать решение со сложностью O (n)?
Да, можно решить эту задачу за линейное время O (n) с помощью алгоритма двух указателей. Идея заключается в том, чтобы использовать два указателя — left и right, которые будут указывать на начало и конец текущей команды. Мы будем увеличивать right до тех пор, пока разница между a[right] и a[left] не превышает 5. Когда мы достигаем такой точки, мы увеличиваем left и продолжаем поиск команды. Вот решение задачи на языке Python с использованием алгоритма двух указателей:
n = int(input())
a = list(map(int, input().split()))
a.sort() # сортируем список
left = 0
right = 0
max_team_size = 0
while right < n:
if a[right] - a[left] <= 5:
right += 1
else:
left += 1
team_size = right - left
if team_size > max_team_size:
max_team_size = team_size
print(max_team_size)Мои комментарии
В обоих случаях довольно впечатляюще, метод двух указателей — хороший выбор для этой задачи. В первом случае абсолютно корректное решение было получено с первой же попытки (особенно если не вчитываться в дополнительные комментарии, которые уже не столь хороши). Во втором случае было сначала сгенерировано неэффективное решение, но более-менее верно оценена его временная сложность. Особенно интересно замечание про ситуацию, когда все элементы списка имеют близкие значения. Формально оно не совсем верно, т.к. во внутреннем цикле нет break при достижении разницы больше 5, и алгоритм всегда выполняет n*(n-1)/2 итераций. Но если бы он был (довольно популярный вариант среди новичков — попытка сократить время выполнения, не работающая при большом количестве близких значений), описание было бы исчерпывающим. После замечания о времени работы было сразу же сгенерировано полностью корректное решение. ChatGPT продемонстрировал поведение, очень похожее на возможное поведение «живого» участника-новичка в подобной ситуации.
Что можно заметить даже на этих примерах?
Во-первых, у модели не очень хорошо с математикой. Кажется, что написать правдоподобный код ей гораздо проще, чем сгенерировать корректное рассуждение о чем-то абстрактном за пределами арифметики и простой алгебры (с которыми она более-менее справляется). Ниже приводится забавный пример, где модель в пределах нескольких предложений многократно противоречит сама себе, и легко нарушает законы логики.
Математическая задача, очень похожая на задачу 1
Реши задачу: найди 2 взаимно простых числа, которые в сумме дают X
Хорошо, я могу помочь вам решить эту задачу. Для того, чтобы найти два взаимно простых числа, которые в сумме дают X, нужно выполнить следующие шаги:
1. Выберите произвольное число A, такое что 1 < A < X.
2. Проверьте, является ли A и X-A взаимно простыми числами.
3. Если A и X-A взаимно просты, то вы нашли нужные числа. Если нет, то вернитесь к шагу 1 и выберите другое число.
Например, если X=15, то можно выбрать A=4. Тогда X-A=11. Проверяем, являются ли 4 и 11 взаимно простыми. Они являются, так как их наибольший общий делитель равен 1. Значит, 4 и 11 — это два взаимно простых числа, которые в сумме дают 15. Таким образом, для любого X можно найти два взаимно простых числа, которые в сумме дают X, используя описанный алгоритм.
Хорошо. Есть ли формула, по которой я могу сразу найти два подходящих числа без перебора?
Для нахождения двух взаимно простых чисел, которые в сумме дают заданное число X, можно использовать следующую формулу: Пусть X = p*q, где p и q — два различных простых числа. Тогда можно выбрать A = p-1 и B = q-1. Таким образом, A и B будут взаимно простыми числами, так как p и q различны, а значит, их наибольший общий делитель равен 1. Тогда X-A-B = X — (p-1) — (q-1) = pq — p — q + 2 = (p-1)(q-1). Таким образом, получаем два взаимно простых числа A и B, которые в сумме дают X, без необходимости перебора всех возможных значений. Например, если X=35, то можно выбрать p=5 и q=7. Тогда A=4 и B=6. Проверяем, являются ли 4 и 6 взаимно простыми. Они являются, так как их наибольший общий делитель равен 2. Значит, 4 и 6 не являются двумя взаимно простыми числами, которые в сумме дают 35. Однако, если мы выберем другие простые числа, то мы сможем найти нужные числа с помощью данной формулы.
Как насчет пары чисел 1 и X-1? Являются ли они решением задачи?
Пара чисел 1 и X-1 может быть решением задачи, если X — простое число. Это можно легко проверить, так как если X — простое число, то его единственными делителями будут 1 и X, и следовательно, 1 и X-1 будут взаимно простыми числами. Однако, если X — составное число, то пара чисел 1 и X-1 не будет решением задачи, так как они не обязательно будут взаимно простыми. Например, если X=15, то 1 и 14 не являются взаимно простыми числами, так как их наибольший общий делитель равен 1. Таким образом, пара чисел 1 и X-1 может быть решением задачи только в том случае, если X — простое число. В остальных случаях нужно использовать другие методы для нахождения двух взаимно простых чисел, которые в сумме дают X.
Может ли пара чисел 1 и X, при X>1, быть не взаимно простой?
Если X — простое число, то пара чисел 1 и X будет взаимно простой, так как 1 является наименьшим положительным целым числом и единственным делителем 1, а X является простым числом, которое имеет только два делителя — 1 и само число X. Однако, если X — составное число, то пара чисел 1 и X может быть не взаимно простой. Например, если X=4, то 1 и 4 не являются взаимно простыми числами, так как они имеют общий делитель 1. Таким образом, пара чисел 1 и X может быть не взаимно простой, если X — составное число. Если X — простое число, то пара чисел 1 и X будет взаимно простой.
Какие числа называют взаимно простыми?
Два целых числа называются взаимно простыми, если их наибольший общий делитель равен 1. Другими словами, два числа называются взаимно простыми, если они не имеют общих делителей, кроме 1. Например, числа 9 и 28 не являются взаимно простыми, так как их наибольший общий делитель равен 1. Однако, числа 8 и 15 являются взаимно простыми, так как их наибольший общий делитель также равен 1. Взаимно простые числа играют важную роль в теории чисел, а также в криптографии и других областях математики и информатики.
Являются ли числа 1 и 4 взаимно простыми?
Нет, числа 1 и 4 не являются взаимно простыми, так как они имеют общий делитель 1. В данном случае, 1 является наименьшим положительным целым числом и единственным делителем 1, а 4 имеет делители 1, 2 и 4. Таким образом, наибольший общий делитель чисел 1 и 4 равен 1, а значит, они не являются взаимно простыми.
Твой последний ответ противоречит определению взаимно простых чисел из позапрошлого ответа.
Вы правы, мой предыдущий ответ был неверным. Числа 1 и 4 являются взаимно простыми, так как их наибольший общий делитель равен 1. Действительно, 1 является наименьшим положительным целым числом и единственным делителем 1, а 4 имеет делители 1, 2 и 4. Но наибольший общий делитель чисел 1 и 4 равен 1, так как 1 не является делителем 4, а значит, числа 1 и 4 взаимно простые. Извините за путаницу.
Являются ли взаимно простыми числа 1 и 7?
Да, числа 1 и 7 являются взаимно простыми, так как их наибольший общий делитель равен 1. 1 является наименьшим положительным целым числом и единственным делителем 1, а 7 имеет делители только 1 и 7. Таким образом, наибольший общий делитель чисел 1 и 7 равен 1, а значит, они являются взаимно простыми.
Являются ли взаимно простыми числа 3 и 22?
Нет, числа 3 и 22 не являются взаимно простыми, так как они имеют общий делитель 1. 3 является простым числом, которое имеет только два делителя — 1 и 3. А 22 имеет делители 1, 2, 11 и 22. Таким образом, наибольший общий делитель чисел 3 и 22 равен 1, а значит, они не являются взаимно простыми.
Я хочу найти пару чисел, таких что их НОД=1 и их сумма равна X. Являются ли числа 1 и X-1 подходящим ответом?
Да, числа 1 и X-1 будут подходящим ответом, если X — простое число. Очевидно, что наибольший общий делитель чисел 1 и X-1 равен 1, так как 1 является наименьшим положительным целым числом и единственным делителем 1, а X-1 не имеет других делителей, кроме 1 и самого себя. Также, сумма чисел 1 и X-1 будет равна X, что соответствует условию задачи. Однако, если X — составное число, то пара чисел 1 и X-1 может не быть подходящим ответом, так как X-1 может иметь общие делители с другими числами, которые в сумме с 1 дадут X.
Предложи какую-нибудь формулу для нахождения пары взаимно простых чисел, в сумме дающих X
Существует формула, позволяющая найти пару взаимно простых чисел, сумма которых равна заданному числу X. Она основана на использовании расширенного алгоритма Евклида для нахождения обратного элемента в кольце вычетов. Пусть X — заданное число, для которого мы ищем пару взаимно простых чисел. Тогда можно использовать следующую формулу:
• Найдем обратный элемент k к числу 2 в кольце вычетов по модулю X: 2k ≡ 1 (mod X).
• Если X — нечетное простое число, то парой взаимно простых чисел, сумма которых равна X, будут числа (X-1)/2 и (X+1)/2.
• Если X — четное простое число, то парой взаимно простых чисел, сумма которых равна X, будут числа 2k (X/2k+1) и (X/2k+1 — 2k), где k — найденный обратный элемент к числу 2 по модулю X.
Например, для X=23, мы можем найти обратный элемент к числу 2 по модулю 23: 2×12 ≡ 1 (mod 23). Тогда парой взаимно простых чисел, сумма которых равна 23, будут числа 11 и 12. Эта формула позволяет находить пары взаимно простых чисел, сумма которых равна заданному числу X, для любого простого числа X. Однако, если X — составное число, то данная формула может не дать все возможные пары взаимно простых чисел, сумма которых равна X.
Я не хочу находить все пары чисел, мне достаточно найти хотя бы одну. Но формула для нахождения должна быть максимально простой.
Для нахождения хотя бы одной пары взаимно простых чисел, сумма которых равна заданному числу X, можно использовать следующую простую формулу:
• Если X — нечетное число, то парой взаимно простых чисел, сумма которых равна X, будут числа (X-1)/2 и (X+1)/2.
• Если X — четное число, то парой взаимно простых чисел, сумма которых равна X, будут числа 2 и X-2, если X-2 является простым числом. Если X-2 не является простым числом, то можно рассмотреть следующую пару чисел: 6 и X-6, если X-6 является простым числом.
Например, для X=23, мы можем использовать первую формулу и найти пару взаимно простых чисел, сумма которых равна 23: (23–1)/2=11 и (23+1)/2=12. Данная формула позволяет находить хотя бы одну пару взаимно простых чисел, сумма которых равна заданному числу X, для любого натурального числа X.
Как насчет 1 и X-1?
Если X — простое число, то парой взаимно простых чисел, сумма которых равна X, будут числа 1 и X-1. Это следует из того, что наибольший общий делитель чисел 1 и X-1 равен 1, так как 1 является наименьшим положительным целым числом и единственным делителем 1, а X-1 не имеет других делителей, кроме 1 и самого себя. Однако, если X — составное число, то пара чисел 1 и X-1 может не быть подходящим ответом, так как X-1 может иметь общие делители с другими числами, которые в сумме с 1 дадут X. Поэтому, если мы не знаем, является ли X простым числом, то лучше использовать формулу, которую я предложил ранее.
Например, числа 9 и 28 не являются взаимно простыми, так как их наибольший общий делитель равен 1. Однако, числа 8 и 15 являются взаимно простыми, так как их наибольший общий делитель также равен 1.
Этот вывод подтверждается и в отдельном исследовании, посвященном использованию GPT для решения различных математических задач. Как и ожидалось, олимпиадные задачи оказались для модели очень сложными — фактически, она была полностью бессильна сгенерировать что-либо полезное.
Во-вторых, ситуация с несложными техническими задачами гораздо лучше. Модели известны простейшие алгоритмы и она может их применить в задачах, описанных естественным языком. Но, как заметно даже в примерах выше — результат очень сильно улучшается при вмешательстве человека, даже небольшом («какая временная сложность решения? придумай эффективнее!»). Если этого не делать, и замерять эффективность «чистой» модели, без наводящих вопросов, обратной связи и контекста — результат действительно не очень хороший.
Каков итог? Рассматривать ChatGPT в качестве самостоятельного участника соревнований пока что не стоит. Но он может быть полезен в качестве «умного ассистента» при живом человеке, который может не только написать код, но и предложить возможные идеи для решения задачи. Можно ожидать, что его использование в таком качестве (особенно в соревнованиях новичков, в Codeforces дивизионах 2–3) будет становиться популярным.
Copilot и CodeWhisperer
Как только речь заходит про «умного ИИ-ассистента для кодинга», конечно же, нельзя не упомянуть Github Copilot (основанный на GPT-3) и Amazon CodeWhisperer, позиционируемых именно в таком качестве. Copilot доступен уже больше года, и судя по отдельным комментариям, регулярно всплывающим на том же Codeforces, активно используется некоторыми участниками соревнований. Полностью свободный доступ к CodeWhisperer был открыт совсем недавно, и отзывов на него пока гораздо меньше.
«Вау-эффекта», подобного ChatGPT или AlphaCode, Copilot пока что скорее не вызвал, в силу своей более узкой направленности. В большинстве случаев люди использовали его как продвинутое средство автодополнения, либо для автоматического написания небольших типовых фрагментов кода без слишком сложной логики. Для редких супер-простых задач этого может быть достаточно, но никаких упоминаний о том, что Copilot способен на что-то большее, пока обнаружить не удалось. Сгенерировать целое решение по тексту задачи — определенно не его сфера. Кажется, что стоит рассматривать Copilot только как способ сократить время написания кода и снизить количество ошибок, но не как помощника в придумывании чего-либо (чего авторы, впрочем, и не обещали). Поэтому проводить специальное тестирование, пытаться вычислять рейтинг и т.п. не имеет смысла.
Свежие альтернативы
Что дальше? Судя по результатам AlphaCode — единственной модели, специально обучавшейся для соревнований — специализация действительно важна (кто бы сомневался
