Поиск связей в социальных сетях
Привет, Хабр! В этом посте мы хотим поделиться нашим решением задачи по предсказанию скрытых связей в корпоративной социальной сети «Улей» компании Билайн. Эту задачу мы решали в рамках виртуального хакатона Microsoft. Надо сказать, что до этого хакатона у нашей команды уже был успешный опыт решения таких задач на хакатоне от Одноклассников и нам очень хотелось опробовать наши наработки на новых данных. В статье мы расскажем про основные подходы, которые применяются при решении подобных задач и поделимся деталями нашего решения.
Постановка задачи и исходные данные
Разработка качественного алгоритма рекомендаций друзей является одной из самых приоритетных задач практически для любой социальной сети т.к. подобный функционал является сильным инструментом для вовлечения и удержания пользователей.
В англоязычной литературе существует достаточно много публикаций по этой теме, а сама задача даже имеет специальную аббревиатуру PYMK (People You May Know).
Компания Билайн в рамках виртуального хакатона от Microsoft предоставила граф корпоративной социальной сети «Улей». 5% ребер в графе была искусственно скрыта. Задача заключалась в поиске скрытых ребер исходного графа.
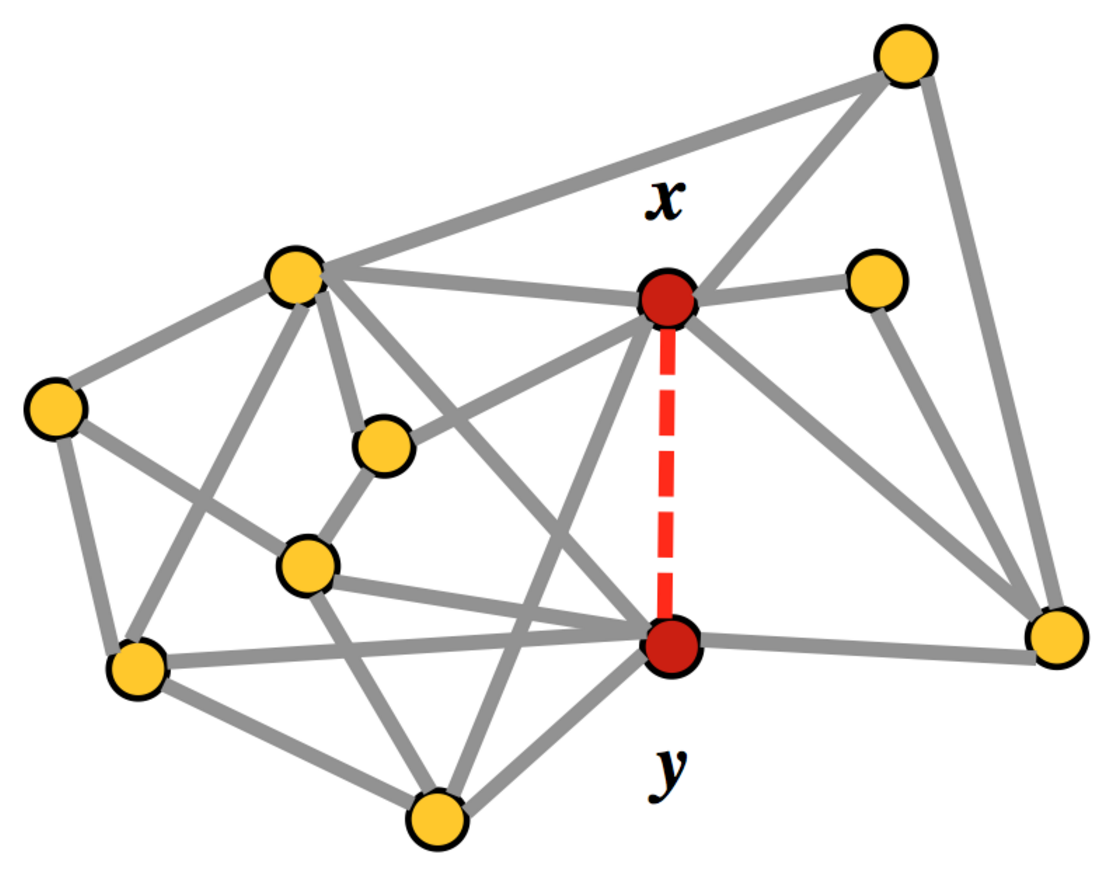
Помимо наличия связи между пользователями социальной сети, для каждой пары также была предоставлена информация о компаниях в которых работают пользователи, информация о числе отправленных и принятых сообщений, длительности звонков и числе отправленных и принятых документов.
Задача поиска ребер сформулирована как задача бинарной классификации, в качестве приемочной метрики была предложена мера F1. В некоторых подобных задачах метрику качества считают отдельно для каждого пользователя и оценивают среднее. В данной задаче качество оценивалось глобально для всех ребер.
Обучение и тест
В общем случае для поиска скрытых ребер в графе необходимо перебрать все возможные пары вершин и для каждой пары получить оценку вероятности наличия связи.
Для больших графов такой подход потребует много вычислительных ресурсов. Поэтому на практике множество кандидатов в социальных графах ограничивают только парами, имеющими хотя бы одного общего друга. Как правило, такое ограничение позволяет заметно сократить объем вычислений и ускорить работу алгоритма без существенной потери в качестве.
Каждая пара кандидатов описывается вектором признаков и бинарным ответом:»1» если ребро есть или »0» в случае отсутствия ребра. На полученном множестве {вектор признаков, ответ} обучается модель, предсказывающая вероятность наличия ребра для пары кандидатов.
Т.к. граф в данной задаче ненаправленный, то вектор признаков не должен зависеть от перестановки кандидатов в паре. Это свойство позволяет при обучении учитывать пару кандидатов только один раз и сократить объем обучающей выборки вдвое.
Чтобы ответить на вопрос какие именно ребра скрыты в исходном графе, оценку вероятности на выходе модели необходимо превратить в бинарный ответ, подобрав соответствующее значение порога.
Для оценки качества и подбора параметров модели мы удалили из предоставленного графа 5% случайно выбранных ребер. Оставшийся граф использовали для поиска кандидатов, генерации признаков и обучения модели. Скрытые ребра использовали для подбора порога и финальной оценки качества.
Ниже описаны основные подходы для генерации признаков в задаче PYMK.
Счетчики
Для каждого пользователя считаем статистики: распределение друзей по географии, сообществам, возрасту или полу. По этим статистикам получаем оценку похожести кандидатов друг на друга, например с помощью скалярного произведения.
Схожесть множеств и общие друзья
Коэффициент Жаккарда — позволяет оценить сходство двух множеств. В качестве множеств могут быть как друзья, так, например, и сообщества кандидатов.
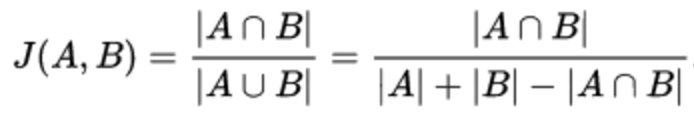
Коэффициент Адамик/Адара — по сути это взвешенная сумма общих друзей двух кандидатов.
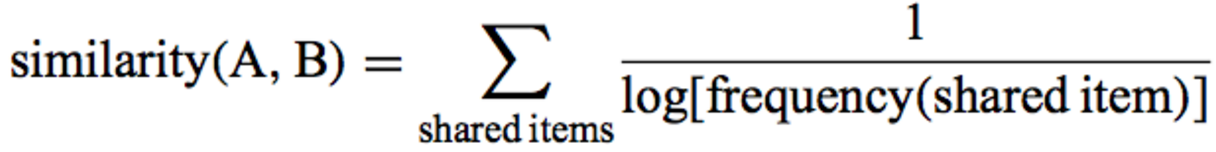
Вес в этой сумме зависит от числа друзей общего друга. Чем меньше друзей у общего друга, тем больший вклад он дает в результирующую сумму. Кстати, именно эту идею мы активно использовали в своем решении.
Латентные факторы
Эти признаки получаются в результате матричных разложений. Причем, разложения можно применять как к матрице связей между пользователями, так и к матрицам сообщество — пользователь, или география — пользователь и им подобным. Полученные в результате разложения вектора с латентными признаками можно использовать для оценки похожести объектов друг на друга, например с помощью косинусной меры расстояния.
Пожалуй самым распространенным алгоритмом матричного разложения является SVD. Также можно использовать популярный в рекомендательных системах алгоритм ALS и алгоритм поиска сообществ в графах BigCLAM.
Признаки на графах
Эта группа признаков вычисляется с учетом структуры графа. Как правило, для экономии времени при расчетах используется не весь граф, а какая-то его часть, например, подграф общих друзей глубины 2.
Одним из популярных признаков является Hitting Time — среднее число шагов, необходимое для прохождения маршрута от одного кандидата к другому с учетом весов ребер. Путь прокладывается таким образом, что очередная вершина выбирается случайно с вероятностью, зависящей от значений атрибутов ребер, исходящих из текущего узла.
Решение
В решении данной задачи мы активно использовали идею заложенную в коэффициенте Адамик/Адара о том, что не все друзья одинаково полезны. Мы экспериментировали с дисконтирующей функцией — пробовали дробные степени вместо логарифма, а также экспериментировали со взвешиванием общих друзей по различным атрибутам полезности.
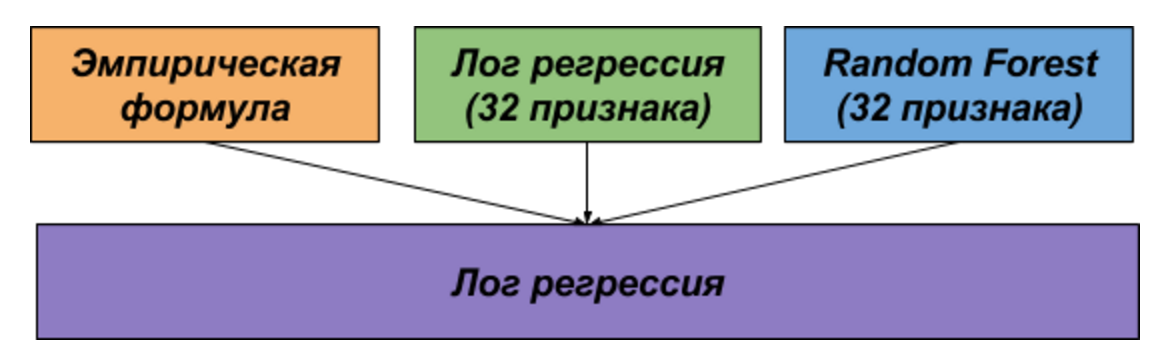
Т.к. над задачей мы работали параллельно, то у нас получилось два независимых решения, которые в последствии были объединены для финального сабмита.
Первое решение основано на идее Адамик/Адара и представляет собой эмпирическую формулу, учитывающую как число друзей общего друга, так и поток сообщений между кандидатами через общих друзей.
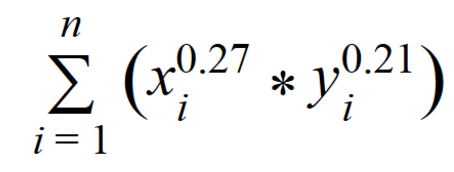
n — количество общих друзей;
xi — количество друзей у общего друга;
yi — сумма входящих и исходящих сообщений между кандидатами через их общего друга
Во втором решении мы сгенерировали 32 признака и обучили на них модель лог. регрессии и random forest.
Модели из первого и второго решения объединяли с помощью еще одной логистической регрессии.
В таблице описаны основные признаки, которые использовались во втором решении.
| признак | описание |
|---|---|
| weighted_commom | Аналог коэффициента Адамик/Адара, но вместо логарифма использовали корень третьей степени |
| conductivity_common | Взвешиваем общих друзей с учетом проводимости сообщений. Чем меньше соотношение исходящих и входящих сообщений/звонков/документов общего друга, тем выше его вес при суммировании |
| flow_common | Оцениваем проходимость сообщений/звонков/документов между кандидатами через общего друга. Чем выше проходимость, тем больше вес при суммировании |
| friends_jaccard | Коэффициент Жаккарда для друзей кандидатов |
| friend_company | Похожесть на основе доли друзей пользователя из компании кандидата |
| company_jaccard | Оцениваем дружественность компаний кандидатов с помощью коэффициента Жаккарда (равен единице, если кандидаты из одной компании) |
Ниже в таблице приведены оценки качества как отдельно, так и результирующих моделей
| Модель | F1 | Точность | Полнота |
|---|---|---|---|
| Эмпирическая формула | 0.064 | 0.059 | 0.069 |
| Лог регрессия | 0.060 | 0.057 | 0.065 |
| Random forest | 0.065 | 0.070 | 0.062 |
| Лог регрессия + Random Forest | 0.066 | 0.070 | 0.063 |
| Лог регрессия + Random Forest + Эмпирическая формула | 0.067 | 0.063 | 0.071 |
Подбор порога
Итак, модель обучена. Следующий шаг — это подбор порога для оптимизации приемочной метрики.
В данной задаче мы оптимизировали метрику F1.
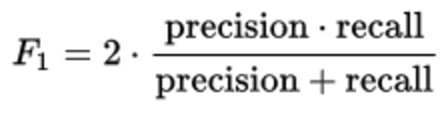
Эта метрика одинаково чувствительна как к точности, так и к полноте и представляет собой гармоническое среднее этих величин.
Т.к. зависимость метрики F1 от порога является выпуклой функцией, то поиск максимума не составляет большого труда.
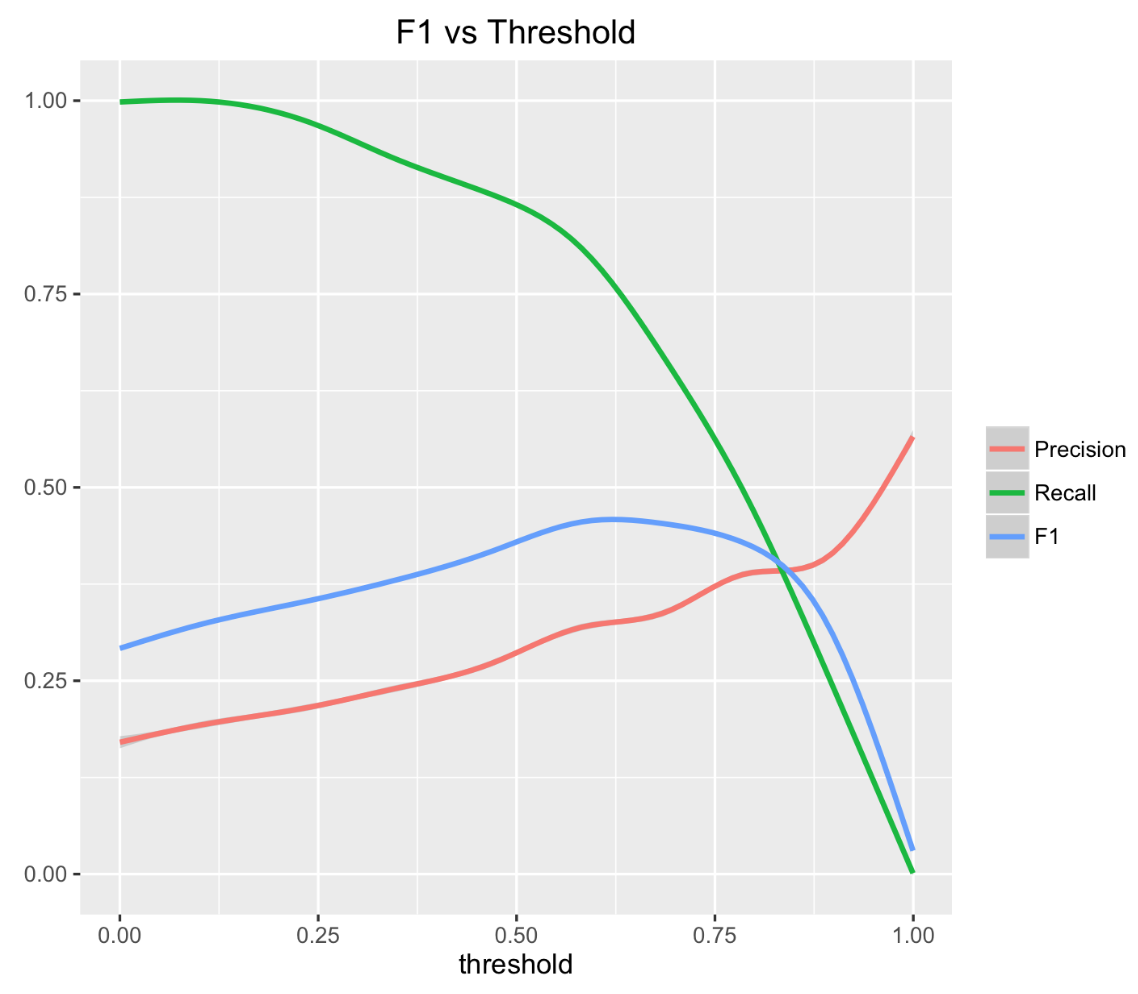
В данной задаче для подбора оптимального значения порога мы воспользовались алгоритмом бинарного поиска.
Технологии
Исходный граф был задан в виде списка ребер с указанием идентификаторов пользователей и соответствующими атрибутами. Всего в обучающей выборке было представлено 5.5 миллионов связей. Исходные данные предоставлены в виде текстового файла формата csv и занимают на жестком диске 163Мб.
В рамках хакатона нам были предоставлены ресурсы облачного сервиса Azure по программе Microsoft BizSpark, в котором мы создали виртуальную машину для наших расчетов. Цена сервера в час составляла $0.2 и не зависела от интенсивности расчетов. Выделенного организаторами бюджета оказалось достаточно для решения данной задачи.
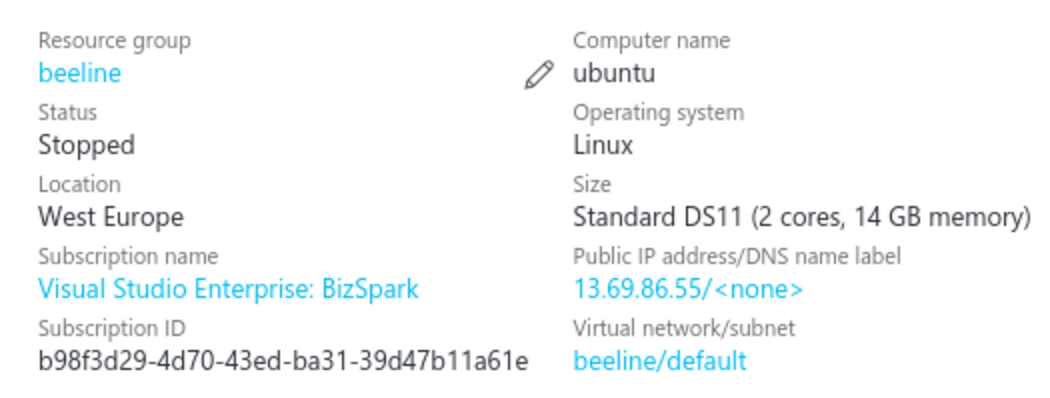
Алгоритм поиска общих друзей мы реализовали на Spark, результаты промежуточных вычислений кешировали на диск в формате parquet, что позволило заметно сократить время чтения даных. Время работы алгоритма поиска общих друзей на виртуальной машине составило 8 часов. Кандидаты со списком общих друзей в формате parquet занимают 2.1Гб.
Алгоритм обучения и подбора параметров модели реализован на python с использованием пакета scikit-learn. Процессы генерации признаков, обучения модели и подбора порога на виртуальном сервере суммарно заняли примерно 3 часа.
В заключении хочется поблагодарить Брагина Ивана за активное участие в решение задачи и креативность в выборе эмпирической формулы.
