Оптимальная аппроксимация сплайнами
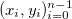и соответствующий им набор положительных весов 
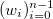. Мы считаем, что некоторые точки могут быть важнее других (если нет, то все веса одинаковые). Неформально говоря, мы хотим, чтобы на соответствующем интервале была проведена красивая кривая таким образом, чтобы она «лучше всего» проходила через эти данные.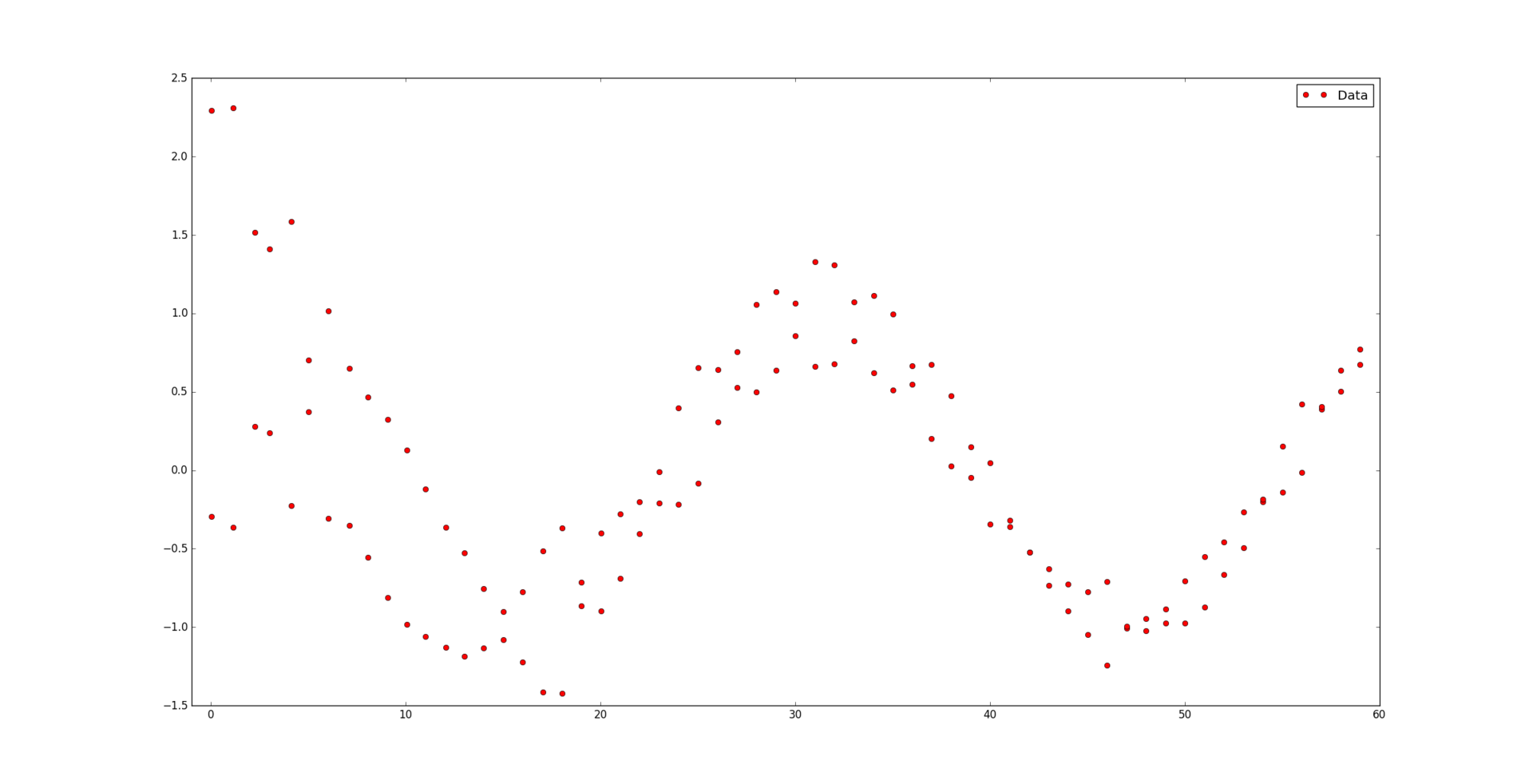 
Под катом находится алгоритм, раскрывающий, каким образом сплайны позволяют строить подобную красивую регрессию: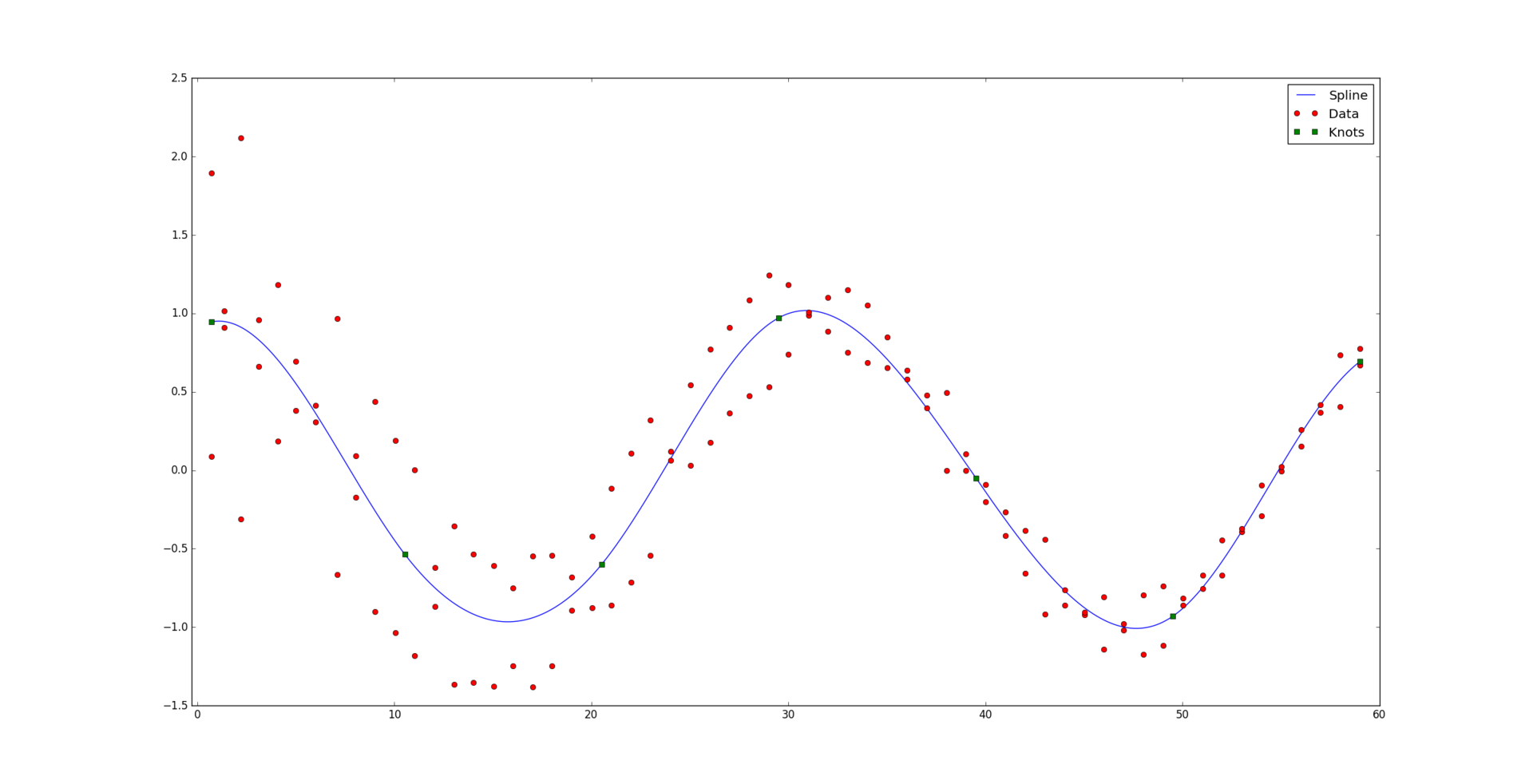 
Основные определения
Функция s (x) на интервале [a, b] называется сплайном степени k на сетке с горизонтальными узлами
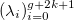, если выполняются следующие свойства: - На интервалах
функция s (x) является полиномом k-й степени. - n-ая производная функции s (x) непрерывна в любой точке [a, b] для любого n = 1, …, k-1.
Заметим, что для построения сплайна нужно для начала задать сетку из горизонтальных узлов. Расположим их таким образом, чтобы внутри интервала (a, b) стояло g узлов, а по краям — k+1:
и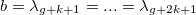 
.Каждый сплайн в точке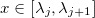 
может быть представлен в базисной форме:
где
— B-сплайн k+1-го порядка: 
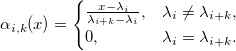
Вот как, например, выглядит базис на сетке из g = 9 узлов, равномерно распределенных на интервале [0, 1]:
Сходу разобраться в построении сплайнов через B-сплайны очень сложно. Больше информации можно найти здесь: www.brnt.eu/phd/node11.
Аппроксимация с заданными горизонтальными узлами
Итак, мы выяснили что сплайн определяется однозначно узлами и коэффициентами. Допустим, что узлы
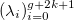нам известны. Также на вход подается набор данных 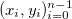с соответствующими весами 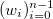. Необходимо найти коэффициенты 
, максимально приближающие кривую сплайна к данным. Строго говоря, они должны доставлять минимум функции
Для удобства запишем в матричном виде:
где
Заметим, что матрица E блочно-диагональная. Минимум достигается когда градиент ошибки по коэффициентам будет равен нулю:
Зададим оператор
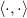, обозначающий взвешенное скалярное произведение: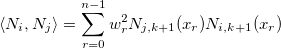 
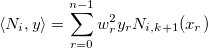
Пусть также
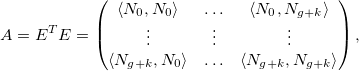
Тогда вся задача и все предыдущие формулы сводятся к решению простой системы линейных уравнений:
где матрица А (2k+1)-диагональная, так как
, если |i — j| > k. Также матрица А симметричная и положительно-определенная, следовательно решение возможно быстро найти с помощью разложения Холецкого (существует также алгоритм для разреженных матриц).И вот, решая систему, получаем желаемый результат:
Сглаживание
Однако, далеко не всегда все так хорошо. При малом количестве данных по отношению к количеству узлов и степени сплайна может возникнуть проблема т.н. сверхподгонки (overfitting). Вот пример «плохого» кубического сплайна, при этом идеально проходящего сквозь данные:
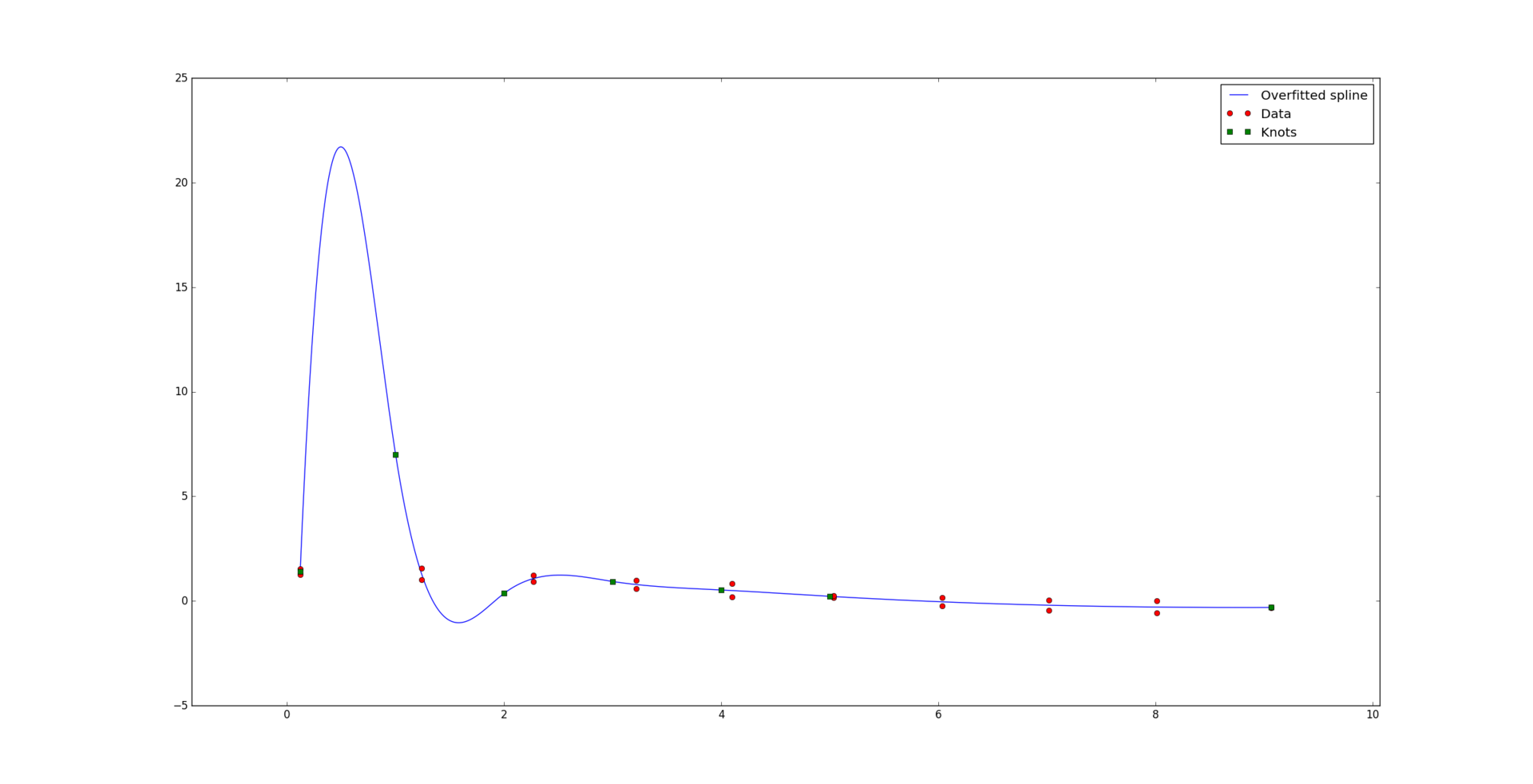
Окей, кривая уже не такая уж и красивая. Попытаемся уменьшить так называемые колебания сплайна. Для этого мы попробуем «сгладить» его k-ю производную. Другими словами, мы минимизируем разницу между производной слева и производной справа от каждого узла:
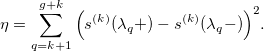
Разложив сплайн в базисную форму, мы получаем:
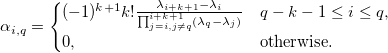
Давайте рассмотрим ошибку
Здесь q — вес функции, влияющей на сглаживание, и
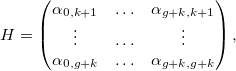
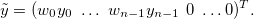
Новая система уравнений:
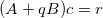
где
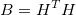
Ранг матрицы B равен g. Она симметричная и, так как q > 0, A + qB будет положительно определенной. Поэтому разложение Холецкого по-прежнему применимо к новой системе уравнений. Однако, матрица B вырожденная и при слишком больших значениях q могут возникнуть численные ошибки.
При совсем маленьком значении q = 1e-9 вид кривой изменяется очень слабо.
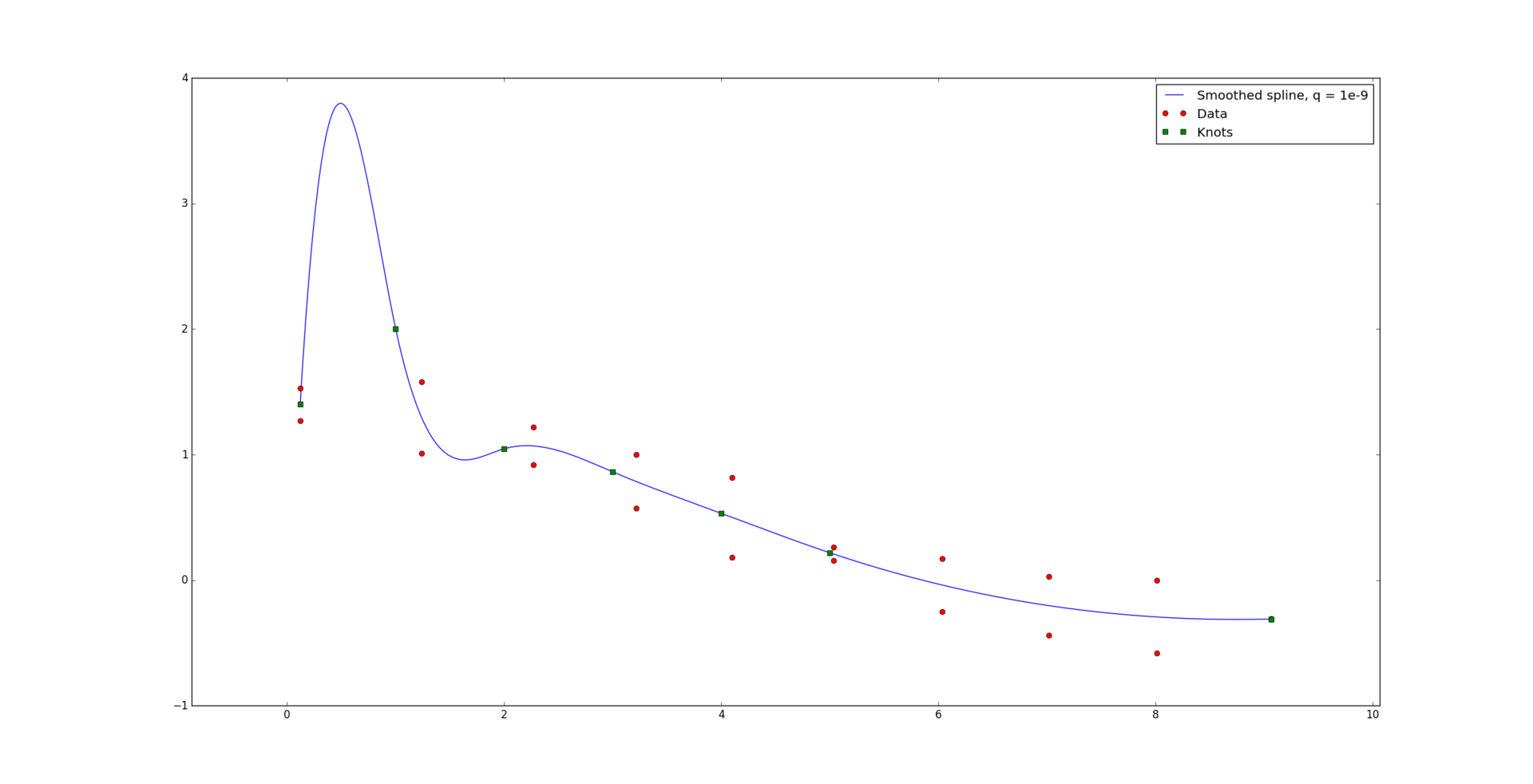
Но при q = 1e-7 в данном примере уже достигается достаточное сглаживание.
Аппроксимация с неизвестными горизонтальными узлами
Представим теперь, что задача такая же, как и прежде, за исключением того, что мы не знаем как узлы расположены на сетке. На вход кроме данных подается только количество узлов g, интервал [a, b] и степень сплайна k. Попробуем наивно предположить, что лучше всего расположить узлы равномерно на интервале:
Упс. Видимо, необходимо все-таки расположить узлы как-то иначе. Формально, расположим узлы таким образом, чтобы значение ошибки
было минимально. Последнее слагаемое играет роль штрафной функции, чтобы узлы не сильно приближались друг к другу:
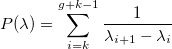
Положительный параметр p — вес штрафной функции. Чем больше его значение, тем быстрее узлы будут удаляться друг от друга и стремиться к равномерному расположению.
Для решения данной задачи мы используем метод сопряженных градиентов. Его прелесть заключается в том, что для квадратичной функции он сходится за фиксированное (в данном случае g) количество шагов.
- Инициализируем направление
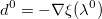. Как рассчитать производную ошибки по узлам?Производная суммы квадратов по узлу:
Для того, чтобы рассчитать влияние положения узла на значения сплайна, нужно рассмотреть B-сплайны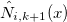
на новых узлах 
и с новыми коэффициентами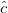 
Производная штрафной функции:
На производную функции сглаживания без слез не взглянешь:
- Для j = 0, …, g-1
- Зададим функцию
возвращающую ошибку в зависимости от выбора шага вдоль заданного направления. На этом шаге мы находим оптимальное значение α*, доставляющее минимум этой функции. Для этого мы решаем задачу одномерной оптимизации. О том, каким образом, будет сказано позже. - Обновляем значения узлов:
- Обновляем вектор направления:
- Зададим функцию
- Если
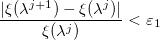
и
где ε1 и ε2 — заранее заданные величины, отвечающие за точность работы алгоритма, то выходим. Иначе, обнуляем счетчик и возвращаемся на первый шаг.
Решение задачи одномерной минимизации
Для того, чтобы найти значение
, доставляющее минимум функции мы используем алгоритм, позволяющий сократить количество обращений к оракулу, а именно количество операций аппроксимации с заданными узлами и подсчета функции ошибки. Мы будем использовать нотацию
.- Пусть первая и последняя компоненты вектора направления равны нулю:
. Зададим также максимально возможный шаг вдоль этого направления: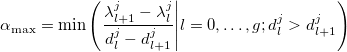 
Такой выбор обусловлен тем, что узлы не должны пересекаться. - Инициируем k = 0 и начальные шаги:
, 
, 
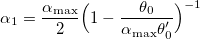. - До тех пор, пока
: - Задаём
и уменьшаем шаг
- k = k + 1
- Задаём
- Если k > 0, то возвращаем α* = α1. Иначе:
- До тех пор, пока
: α0 = α1, α1 = α2 и
- Возвращаем
, где 
— корень уравнения I'(α) = 0 и I (α) — аппроксимация функции ошибки: 
где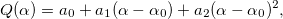
- До тех пор, пока
Коэффициенты ai и bi могут быть найдены из уравнений
и
Объяснение алгоритма:
Идея заключается в том, чтобы расставить три точки α0 < α1 < α2 таким образом, чтобы по значениям ошибок, достигаемых в этих точках, можно было построить простую аппроксимирующую функцию и вернуть её минимум. Притом значение ошибки в α1 должно быть меньше, чем значение ошибки в α0 и α2.
Находим начальное приближение α1 из условия S'(α1)=0, где S (α) — функция вида
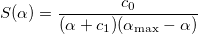
Константы c0 и c1 находятся из условий
и 
.Если мы просчитались с начальным приближением, то мы уменьшаем шаг α1 до тех пор, пока он доставляет большее значение ошибки, чем α0. Выбор 
исходит из условия 
, где Q (α) — парабола интерполирующая функцию ошибк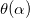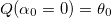и 
: 
, 
и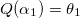 
.
Если k > 0, то мы нашли значение α1, такое что при его выборе значение ошибки будет меньше, чем при выборе α0 и α2, и мы возвращаем его в качестве грубого приближения α*.
Если же наше первоначальное приближение было верным, то мы пытаемся найти шаг α2, такой что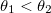 
. Он будет найден между α1 и αmax, так как αmax — точка сингулярности для штрафной функции.
Когда найдены все три значения α0, α1 и α2, мы представляем функцию ошибки в виде суммы двух функций, приближающих разность квадратов и функцию штрафа. Функция Q (α) — парабола, чьи коэффициенты могут быть найдены, так как мы знаем её значения в трех точках. Функция R (α) уходит на бесконечность при α, стремящемся к αmax. Коэффициенты bi также могут быть найдены из системы из трех уравнений. В результате, мы приходим к уравнению, которое может быть приведено к квадратному и легко решено:
И вот, для сравнения, результат оптимально построенного сплайна: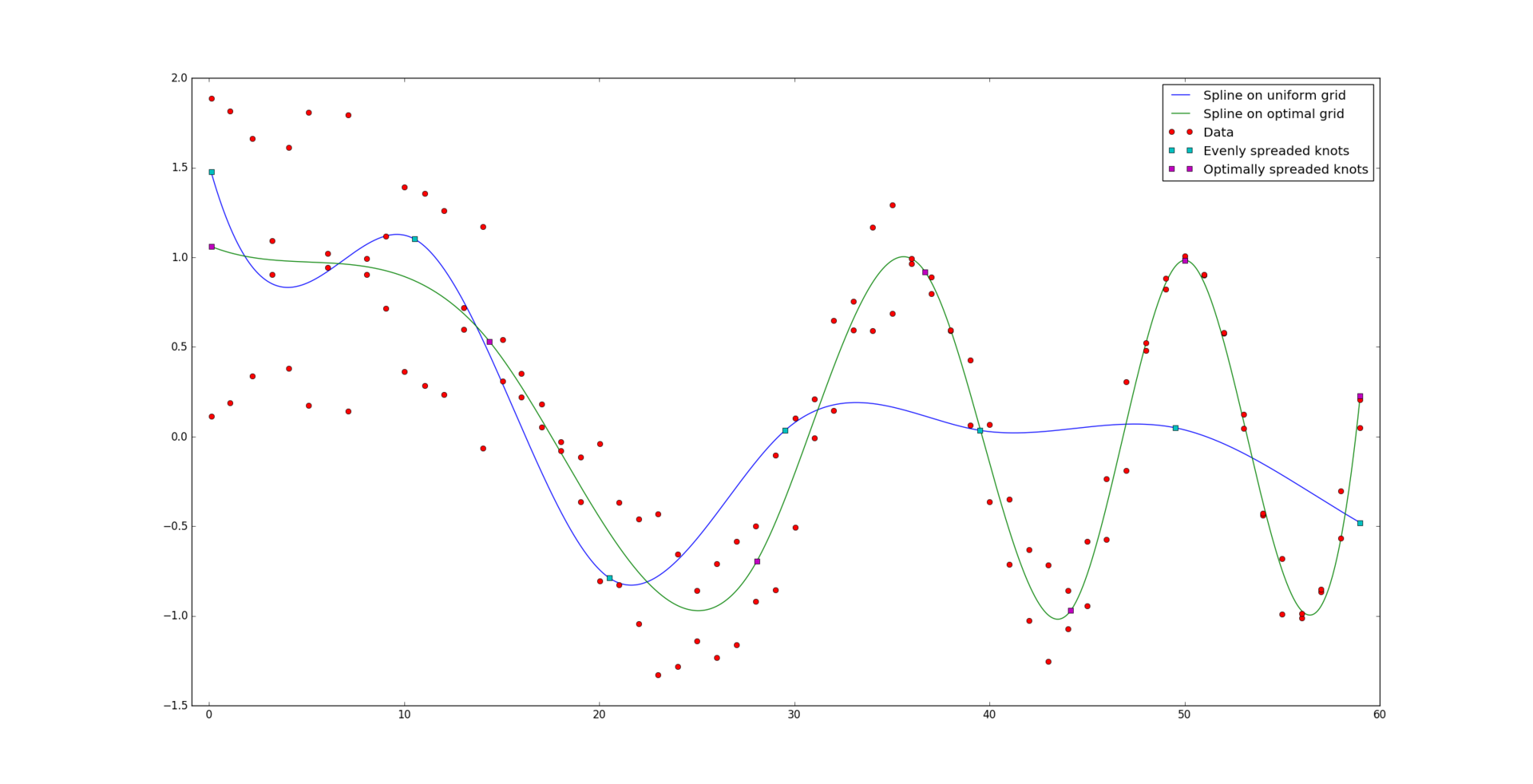 
Ну и для тех, кому может пригодиться: реализация на Python.
Комментарии (1)
gudvinr
7 декабря 2016 в 21:54
0↑
↓
У вас есть возможность собрать пакет для PyPI?
