Об одном индикаторе, применимом для наглядной оценки быстро возрастающих функций
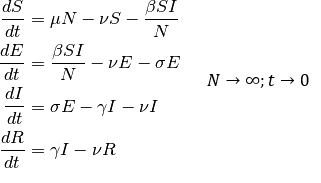
Для многих моделей эпидемий — SIR, SEIR и подобных (детали математического описания см., например, в www.idmod.org/docs/hiv/model-compartments.html) справедливо следующее утверждение: на начальном этапе эпидемии, когда количество заразившихся (I) много меньше размера популяции, скорость роста количества заболевших пропорциональна количеству заболевших:
, где β — коэффициент, характеризующий скорость заражения.
Решением данного уравнения является показательная функция. Для показательной функции справедливо следующее функциональное уравнение:
Т.о. число является периодом удвоения для функции
. По определению, если период удвоения для гладкой неубывающей функции является константой, то функция — показательная.
Как и многие другие в это интересное время, я слежу за графиками роста заболеваемости, публикуемыми, к примеру, на сайте.
Уже довольно давно графики стали напоминать нечто, похожее на бумеранг или хоккейную клюшку:

Рисунок 1
Те же графики в логарифмическом масштабе дают чуть больше информации:

Рисунок 2
Видно, что темпы роста имеют тенденцию к замедлению, поскольку наклон логарифма от соответствующей функции уменьшается, но все же есть неудовлетворенность от непонимания, насколько всё-таки действенны применяемые меры по сдерживанию эпидемии.
Реальная динамика количества заражённых даже в условиях применимости приближения отличается от экспоненциальной, что обусловлено в первую очередь мерами по сдерживанию эпидемии, которые приводят к тому, что
перестаёт быть константой и становится убывающей (если меры эффективные, разумеется) функцией от времени.
В связи с вышеизложенным в качестве индикатора, применимого для наглядной оценки функций, похожих на показательную, предлагается использовать период удвоения. В общем случае для монотонно возрастающей функции период удвоения
можно определить из следующего функционального уравнения:
Отличие от константы свидетельствует об отличии
от экспоненты. Применительно к динамике показателей заболеваемости, рост
(в идеале — к бесконечности) свидетельствует об эффективности принимаемых мер по сдерживанию эпидемии.
В случае функций, заданных таблично на дискретном множестве, например, в виде таблицы зависимости количества заболевших от даты, существует произвол в определении . В качестве простейшего способа определения
можно предложить следующий:
Пусть t∈{0;1; …; N}-дискретное время, I (t) — количество заболевших в зависимости от времени t. Тогда

Также можно определить «пессимистичный» период удвоения

«Пессимизм» в данном случае связан с тем, что сравнение I (t) производится всегда с I (o), т.е. с «низкой» по определению базой. Но мы ведь предполагаем, что с течением времени ситуация должна улучшаться? Для оптимистов есть своё определение:

Согласно вышеприведённым определениям

Ниже приведены примеры применения вышеописанного индикатора:

Рисунок 3
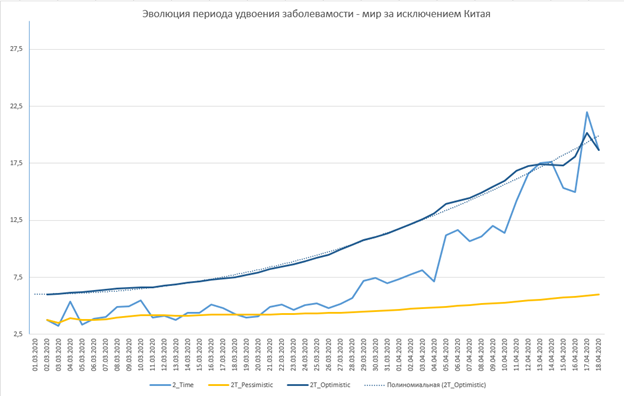
Рисунок 4
Данные по Испании, описанной в прессе как пример головотяпства

Рисунок 5
Несмотря на очевидное головотяпство на начальном этапе, Испания всё же выглядит небезнадежно.
И в заключение — родные пенаты

Рисунок 6
Утешает, что в Роспотребнадзоре темпы прироста заболеваемости COVID-19 в РФ сочли медленными.
Файл с исходными данными, формулами и графиками можно взять здесь
Домашние задания:
1. Решить относительно уравнение
для следующих функций
, где
— гамма функция
Также для решить уравнение
2. Ответить на вопрос: как связаны определённый выше период удвоения функции и логарифмическая производная функции?
Прошу читателей в течение недели не публиковать решения в комментариях.
