Новый класс простых чисел, который я открыл случайно03.05.2021 12:33

Всем привет! Это мой первый пост на Хабре, потому я представлюсь: меня зовут Костя, я разработчик C++, немного музыкант, начинающий ML инженер и любитель математики. Как не сложно догадаться этот пост будет о моём математическом хобби.

Предыстория: порядка 14 лет назад я столкнулся с феноменом циклических чисел, я был заворожен закономерностями которые в них образуются и пообещал себе объяснить их. Вначале я предпринимал наивные попытки анализа, которые принесли очень посредственные результаты, однако в 2016 году мне удалось самостоятельно увидеть что рациональная дробь 1/7 может быть представлена сходящейся геометрической прогрессией. Признаюсь честно в тот момент я даже не понял что это геометрическая прогрессия, но распознал её визуально. В 2018 году я решил приложить все свои навыки и старание чтобы найти как можно больше закономерностей циклических чисел. Я нашел очень много, но сейчас хочу поделиться тем, которое считаю самым важным, и по иронии — найденным мной случайно: новый класс простых чисел.

Я занимался исследованием full reptend prime, простых чисел, а если быть более точным — таких систем счисления для простых чисел, в которых 1/P, где P — простое число, будет давать периодическую дробь, период которой будет равен циклическому числу.

Здесь нужно пожалуй привести само определение циклического числа:

Циклическое число — это целое число, циклические перестановки которого являются произведением этого числа на последовательные числа.

Самое известное циклическое число — 142857, которое было популяризировано псевдонаучными концепциями «эннеаграммы» + вторая ссылка. Но я так же встречал его в научно популярных книгах, в частности в занимательной математике Перльмана. Не того гения, который доказал гипотезу Пуанкаре, а Якова Исидоровича Перьмана, жившего на век раньше и занимавшегося популяризацией науки. Это была несколько детская, но интересная книга «Занимательная арифметика. Загадки и диковинки в мире чисел».

Рассмотрим циклические перестановки этого числа:

142857×2 = 285714

142857×3 = 428571

142857×4 = 571428

142857×5 = 714285

142857×6 = 857142

Как можно увидеть, при умножении изначального числа 142857 на числа от 2 до 6, мы получаем циклические перестановки числа 142857. Когда я впервые это увидел мне это показалось настоящей магией.

Как я говорил выше, в один момент я заметил что 1/7 может быть представлена геометрической прогрессией. Позже я заметил что это не единственная сходящаяся геометрическая прогрессия для 1/7, я увидел ещё одну. Потом ещё одну.

Я наконец потом я заметил что у 1/7 была бесконечность сходящихся геометрических прогрессий. Окей формулы будут ниже! И вот вот я уже перейду к изложению математики, но эта преамбула была нужна чтобы объяснить, что исследуя эту формулу — я случайно нашёл тот самый класс простых чисел о которым я говорю, а потом мне посчастливилось найти в нем очень необычные закономерности.

Теперь немного исторической справки, наверное многим, как и мне стало интересно, когда люди впервые узнали о таком свойстве простого числа 7 в десятичной системе счисления. Не удивительно -, но вся литература будет зарубежной.

Первое упоминание, связанное с циклическими числами и full reptend prime, встречается в книге«The Philisophy of Arithmetic: Exhibiting a Progressive View on the Theory and Practice of Calculation».

Эта книга была опубликована за 200 лет до текущей работы, однако уже тогда была сформулирована возможность разложения периодической дроби в форме сходящейся геометрической прогрессии. Авторы книги не используют термин «геометрическая прогрессия», однако они успешно показывают разложение дроби 1/7 на сумму уменьшающихся дробей.

В книге «History of the Theory of Numbers» встречается формулировка условия, при котором возникают full reptend prime.

В книге «The Penguin Dictionary of Curious and Interesting Numbers» можно найти упоминания о циклических числах и их связи с repunit.

В книге «The Book of Numbers» присутствует упоминание остатков от деления при образовании периодической дроби, которые впоследствии используются в формуле геометрических прогрессий.

Однако ни в этих книгах, ни в интернетах я не смог найти информацию, которую я открыл самостоятельно, чему был сильно удивлен, потому спешу поделиться ей в этой статье. И так дальше вас ждёт непосредственно математика.

Циклические простые числа

Первым циклическим простым числом, образованным от 142857, является 1428571, это число простое. Такое число можно записать по первой цифре изначального циклического числа и общему количеству цифр. Например, для 1428571 первая цифра это 1, и общее число цифр — 7.

Приведем все простые числа, образованные от циклического числа 142857, и не превышающие титанические простые числа (до 10 тысяч цифр). Первые числа записаны целиком, более длинные описываются первой цифрой и количеством цифр.

Первые 7 циклических простых чисел, образованных от числа 142857: 1428571, 71428571, 7142857142857, 571428571428571, 1428571428571428571428571, 28571428571428571428571428571, 7142857142857142857142857142857.

Количество цифр в этих числах в десятичной системе счисления: 7, 8, 13, 15, 25, 29, 31.

Дальнейшие числа очень длинные и будут представлены только первой цифрой и количеством цифр.

Первая цифра	Число цифр
2	34
4	41
7	104
5	273
5	304
1	355
7	440
7	571
1	823
7	2215
5	2523
4	4379
2	4510
4	7553
4	7679
7	9536

Всего 23 простых числа, не превышающих 101000.

Свойства простых чисел в зависимости от системы счисления. Full reptend prime

Для того, чтобы рассмотреть, как возникают циклические простые числа, нам нужно также рассмотреть, как возникают циклические числа.

Существует класс простых чисел под названием full reptend prime или long prime. Соответствующего названия на русском языке нет. Данный класс простых чисел зависит от системы счисления, это значит, что каждое простое число является full reptend в некоторой системе счисления.

Простое определение full reptend и циклического числа

P — простое число, если периодическая дробь, образованная в ходе вычисления рациональной дроби 1/P, в некоторой системе счисления N имеет период, равный P-1, то можно говорить, что простое число P в N системе счисления является full reptend.

Если число P является full reptend в некоторой системе счисления N, то все P-1 его цифр образуют циклическое число.

Более сложное определение

Если система счисления взаимно проста по отношению к числу P, то частное Ферма будет являться целым числом, на основании малой теоремы Ферма. Если система счисления является первообразным корнем мультипликативной группы кольца вычетов по модулю P, то тогда частное Ферма — циклическое число, а P — full reptend prime.

Рассмотрим простое число P = 7 в десятичной системе счисления. Число образованное от 1/P = 0,(142857). Период равен 6, что равно P-1. Рассмотрим остальные дроби из множества 1/P … P-1/P:

2/P = 0,(285714)

3/P = 0,(428571)

4/P = 0,(571428)

5/P = 0,(714285)

6/P = 0,(857142)

Мы наблюдаем, что в данной дроби сохраняется свойство циклической перестановки. Ниже будет представлена одна из визуализаций. В этой таблице каждая строка представляет собой простое число, они указаны слева. Каждый столбец представляет собой систему счисления, они указаны сверху. Значение в ячейке — длина периода дроби 1/P. Зеленым цветом выделены ячейки которые являются full reptend.

Вначале разберем отдельные части этой таблицы:

Для каждого простого числа P есть последовательность из возможных длин периода дроби 1/P. Длина этой последовательности равна P. Для P = 2 длина цикла систем счисления равна 2, для P = 3 длина цикла систем счисления равна 3, и т.д.

Для расчета длины периода в некоторой системе счисления необходимо найти такое n:

(система счисленияn) mod P = 1

Ниже приведена таблица для разных P в разных системах счисления:

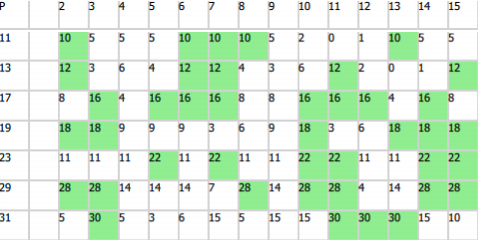
В десятичной системе счисления мы видим, что первые простые числа, являющиеся full reptend, это 7, 17, 19, 23, 29. Числа 2 и 5 не имеют здесь периода, поскольку основание системы счисления делится на оба этих простых числа без остатка.

В случае P = 3 мы получаем периодическую дробь с единичной длиной периода в десятичной системе: ⅓ = 0,(3). В случае P = 11 мы получаем периодическую дробь с длиной периода, равной 2 в десятичной системе: 1/11 = 0,(09).

При P = 13 мы получим особый случай, длина периода равна 6, что не равно P-1. Однако длина периода равна (P-1)/2, когда соблюдается такая пропорция, образуется два набора циклических чисел. Такое число P называется 2nd reptend level prime. Приведем пример 2nd reptend level prime:

1/13 = 0,(076923)

2/13 = 0,(153846)

Все другие дроби от P = 13, вплоть до P-1/P, будут состоять из тех же цифр, что и 1/13 или 2/13, нос циклическими перестановками.

3/13 = 0,(230769) — цикл 1

4/13 = 0,(307692) — цикл 1

5/13 = 0,(384615) — цикл 2

6/13 = 0,(461538) — цикл 2

7/13 = 0,(538461) — цикл 2

8/13 = 0,(615384) — цикл 2

9/13 = 0,(692307) — цикл 1

10/13 = 0,(769230) — цикл 1

11/13 = 0,(846153) — цикл 2

12/13 = 0,(923076) — цикл 1

2nd reptend level prime тоже образуют циклические простые числа: от каждой из последовательностей цифр могут образовываться простые числа.

Т.е. существуют простые числа: 769230769, 769230769230769230769,769230769230769230769230769230769.

Но также и: 1538461.

Также в завершение этой темы интересно отметить, что системы счисления, в которых мы встречаем full reptend prime, тоже являются необычными. Для P = 7 первые 2 системы счисления, в которых оно является full reptend, это системы с основанием 3 и 5 — простые числа близнецы.

Далее эти точки повторяются через каждые 7 систем счисления. Когда сумма оснований систем счисления делится без остатка на 12, мы встречаем снова простые числа близнецы. Например, 17 и 19, 59 и 61.

Представление периодической дроби в форме сходящейся геометрической прогрессии

Каждая из дробей, образованных full reptend или n-th repntend level может быть разложена на сходящиеся геометрические прогрессии. Для каждого простого числа P и заданной системы счисления N существует бесконечное количество таких геометрических прогрессий.

Формула для записи суммы геометрической прогрессии для 1/P:

$\begin{equation} \sum\limits_{n=0}^\infty\frac{s*r^n}{base^{length(n+1)}} = \frac{1}{P} \end{equation}$

Где s — это целое число, полученное из дроби 1/P:

$\begin{equation} s=[\frac{1}{P}*base^{length}] \end{equation}$

Поскольку full reptend prime образуют бесконечную периодическую дробь, мы можем получить из нее числа с количеством цифр от 1 до бесконечности. Ну условно конечно :)

Параметр length означает количество символов, которые будут использованы в числе s, это число может варьироваться от единицы до бесконечности. При каждом новом параметре length мы будем получать новую геометрическую прогрессию.

Число r тоже является целым и представляет собой один из остатков от деления, образованны при вычислении 1/P. Как дробь 1/P будет иметь период P-1, в случае если простое число являетсяfull reptend в исследуемой системе счисления, точно так же количество остатков будет равно P-1.

Для того, чтобы понять, как образуются остатки от деления, рассмотрим их на примере. Возьмем P= 7, т.к. это первое full reptend в привычной нам десятичной системе счисления.

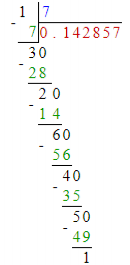
В итоге мы получили уникальные остатки: [3, 2, 6, 4, 5, 1]. Именно эти значения будут принимать участие в формуле. Первый остаток от деления будет равен base mod P. Каждый последующий остаток будет зависеть от предшествующего, функцию можно записать рекурсивно:

$\begin{equation} \begin{cases} r_0 = 1 \\ r_n = r_{n-1} * (base\mod P) \\ \end{cases} \end{equation}$

Переведем рекурсивную формулу в замкнутую форму:

$\begin{equation} r_{length}=base^{length}\mod P \end{equation}$

Запишем общую формулу геометрической прогрессии, используя только следующие параметры: P— простое число; base — исследуемая система счисления; length — параметр, определяющий номер геометрической прогрессии для данного простого числа и данной системы счисления.

$\begin{equation} \frac{1}{P} = \sum\limits_{n=0}^\infty\frac{[\frac{1}{P}*base^{length}]*(base^{length}\mod P)^n}{base^{length(n+1)}} \end{equation}$

Приведем формулы для P = 7 c использованием разных s, начиная с самых коротких:

$\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{1*3^n}{10^{n+1}} \end{equation}$

В данной формуле s = 1, это первая цифра из дроби 0,(142857), т.е. параметр length = 1.При этом остаток r = 3, это самый первый остаток, что соответствует параметру length = 1.

$\begin{equation} \frac{1}{7} = 0.1 + 0.03 + 0.009 + 0.0027 + 0.00081 + .. \end{equation}$

Каждый следующий член прогрессии получается посредством умножения на 3 и деления на 10. Теперь рассмотрим следующую прогрессию:

$\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{14*2^n}{10^{2(n+1)}} \end{equation}$ $\begin{equation} \frac{1}{7} = 0.14 + 0.0028 + 0.000056 + 0.00000112 + .. \end{equation}$

В данной формуле каждый следующий член прогрессии получается посредством умножения на 2 и деления на 100. Здесь s = 14, это первые две цифры из дроби 0,(142857), т.е. параметр length = 2. При этом остаток r = 2, это второй остаток, что соответствует параметру length = 2. Есть интересные закономерности, которые можно исследовать связанные с этим, но я приберег это для отдельной статьи, которую я так же обязательно опубликую в том числе на Хабре.

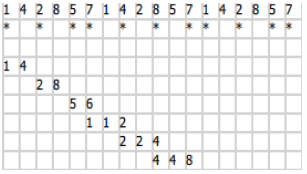
Дальнейшие формулы по аналогии с предшествующими будут получены просто последовательным увеличением значения length на 1:

$\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{142*6^n}{10^{3(n+1)}} \end{equation}$ $\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{1428*4^n}{10^{4(n+1)}} \end{equation}$ $\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{14285*5^n}{10^{5(n+1)}} \end{equation}$ $\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{142857*1^n}{10^{6(n+1)}} \end{equation}$

И наконец мы получаем последовательность, в которой s представляет собой простое число:

$\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{1428571*3^n}{10^{7(n+1)}} \end{equation}$

Собственно когда я факторизировал все возможные s — что к слову представляло для меня интерес по другой причине, я нашел что некоторые из них сами по себе простые. Так собственное я и совершил это небольшое открытие. Но это не всё что мне удалось найти про эти простые числа.

На этом можно отложить рассмотрение дальнейших геометрических прогрессий, однако важно заметить, что их может быть бесконечное множество, так как чисел s для каждого числа P в некоторой системе счисления N — бесконечное множество.

Приведем также в пример несколько сходящихся геометрических прогрессий для P = 17:

$\begin{equation} \frac{1}{17} = \sum\limits_{n=0}^\infty\frac{5*15^n}{10^{2(n+1)}} \end{equation}$ $\begin{equation} \frac{1}{17} = \sum\limits_{n=0}^\infty\frac{58*14^n}{10^{3(n+1)}} \end{equation}$ $\begin{equation} \frac{1}{17} = \sum\limits_{n=0}^\infty\frac{588*4^n}{10^{4(n+1)}} \end{equation}$

Интересно рассмотреть разложение числа 89 на геометрические прогрессии. 1/89 = 0,0112359… — можно увидеть, как в первых цифрах дроби наблюдаются числа Фибоначчи. И действительно эту дробь можно разложить не только на сходящуюся геометрическую прогрессию, но и описать формулой с числами Фиббоначи:

$\begin{equation} \frac{1}{89} = \sum\limits_{n=0}^\infty\frac{1*11^n}{10^{2(n+1)}} \end{equation}$ $\begin{equation} \frac{1}{89} = \sum\limits_{n=0}^\infty\frac{Fibonacci(n)}{10^{n+1}} \end{equation}$

Интересно, что схожее явление можно встретить в другом простом числе — 109.

Формула для этого числа отличается от формулы 1/89 только множителем: 2*(n%2) — 1. Этот множитель приводит к тому, что происходит не только суммирование, а чередование суммирования и вычитания разных элементов прогрессии.

$\begin{equation} \frac{1}{109} = \sum\limits_{n=0}^\infty\frac{9*17^n}{10^{3(n+1)}} \end{equation}$ $\begin{equation} \frac{1}{109} = \sum\limits_{n=0}^\infty\frac{Fibonacci(n)*(2(n\mod2)-1))}{10^{n+1}} \end{equation}$

Возможно, существуют и другие разложения периодической дроби, помимо сходящихся геометрических прогрессий и суммирование чисел Фибоначчи.

Образование циклических и суб-циклических простых чисел

Когда мы будем рассматривать разные значения s из формулы геометрической прогрессии, мы заметим, что среди них будут встречаться простые числа.

Например, для простого числа P = 7, образующего циклическое число 142857, первым простым числом будет 1428571. Далее будет возникать большое количество подобных чисел, для того чтобы рассмотреть все возможное их множество, нужно рассматривать не только геометрические прогрессии 1/P, но и все другие прогрессии из множества 1/P … P-1/P. Иначе мы могли бы пропустить, например, простое число 71428571.

Предположительно, в каждой системе счисления таких чисел бесконечное множество. Однако, мне не удалось найти закономерность их возникновения. Возможно, таких чисел ограниченное количество, и если это так, на мой взгляд это было бы даже интересней, но я предполагаю, что их множество бесконечно.

На самом деле, если мы внимательно рассмотрим параметр s, мы встретим в нем простые числа, которые будут меньше, чем циклическое число, однако будут содержать последовательность цифр из циклического числа. Такие числа можно назвать простыми суб-циклическими числами.

Рассмотрим их на примере P = 7. Если мы будем одновременно рассматривать не только 1/P, но и все другие дроби вплоть до P-1/P, то мы увидим, что среди параметров s встречается множество других простых чисел: 2, 5, 7, 71, 571, 2857, 28571.

В отличие от циклических простых чисел, множество суб-циклических простых чисел всегда ограничено.

Циклические и суб-циклические простые числа могут быть образованы от любого простого числа P в некоторой системе счисления N. Это является следствием того, что каждое простое число может быть full reptend prime в некоторой системе счисления.

Связи между циклическими простыми числами, образованными от одного простого числа в разных системах счисления

Как было сказано ранее, циклическое простое число может быть получено от любого простого числа в некоторых системах счисления. Для каждого конкретного циклического простого числа есть простое число P и система счисления N, с помощью которых было образовано циклическое простое число. Однако циклические простые числа, образованные от одного P, но в разных системах счисления, могут проявлять свойства позволяющие их группировать.

Наконец десерт — это то что мне нравится больше всего:

Однако циклические простые числа, образованные от одного P, но в разных системах счисления, могут проявлять свойства позволяющие их объединять в группы. Например, в десятичной системе счисления мы получаем простые числа из циклического числа 142857. А в 40 системе счисления мы получаем простые числа из циклического числа 5SMYBH (что соответствует последовательности цифр 5, 28, 22, 34, 11, 17).

Однако, если мы возьмем простое число, которое оригинально выглядит как H5SMYBH в 40 системе счисления, и переведем его в десятичную систему счисления, мы увидим некоторую закономерность: 70217142857.

Младшие разряды будут соответствовать процессу образования циклических простых чисел, но в старших разрядах будут отклонения. Если написанное выше было непонятно, я приведу несколько чисел образованных в десятичной системе счисления, и представленных как в десятичной, так и в сороковой.

Вот простые числа в десятичной системе счисления образованные от P=7 N=10:

1) 1428571

2) 71428571

3) 7142857142857

4) 571428571428571

5) 1428571428571428571428571

6) 28571428571428571428571428571

7) 7142857142857142857142857142857

8) 2857142857142857142857142857142857

9) 42857142857142857142857142857142857142857

Те же самые числа представленные в 40 системе счисления:

1) MCYB

2) Ra2YB

3) 13NYIMYBH

4) 277Sb5SMYB

5) 1D8TJS2CYBH5SMYB

6) GP98QAT0SMYBH5SMYB

7) 2NbRO471EIMYBH5SMYBH

8) PdGa11UDOPSMYBH5SMYBH

9) 3WAEQ3OR61AQVH5SMYBH5SMYBH

Пример чисел образованных от P=7 N=10 в сороковой системе счисления:

1) H5SMYBH

2) Следующее число днинное — 77 цифры длиной, оно начинается с 5SMYBH, и повторяется до B:

5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYB

А вот те же самые числа в десятичной системе счисления:

1) 70217142857

Следующее число очень длинное — его циклическая часть содержит 12 полных циклов, и все число целиком занимает 123 числа.

2) 3262280440470765442418939358741703168874849426…

…28571428571428571428571428571428571428571428571428571428571428571428571428571

Следующие числа я не привожу из-за их чрезмерной длины, однако закономерности в них сохраняются так же.

Формула для вычисления систем счисления, образующих связи с оригинальной системой счисления для заданного простого числа

Выше мы рассмотрели простое число P = 7 и систему счисления N = 10. Обобщенно формулу для нахождения связанных систем счисления можно записать так:

Ns (i) = N + 3*N*i + (i + 1% 2) * i*N*4

Где i — это натуральное число. И i = 0 соответствует первой системе, в которой простое число является full reptend prime. Однако эта формула подходит исключительно для десятичной системы счисления.

Если мы попробуем выписать подобные формулы хотя бы для нескольких других систем счисления, окажется, что их не так легко обобщить.

Формула для N = 3, 10, 17, 31, 38, 59:

Ns (i) = N + 3*N*i + (i + 1% 2) * i*N

Формула для N = 5, 19, 26, 33, 47, 61:

Ns (i) = N + N*i + (i + 1% 2) * i*5*N

Формула для N = 12:

Ns (i) = N + N*i + (i + 1% 2) * i*5*N

N = 40 относится к группе, образованной от N = 10.

Схожее справедливо и для N = 24, она так же образована от N = 12.

Отличие образованных групп заключается в том, что связанные циклические числа начинают образовываться в системах счисления ниже, чем изначальная исследуемая N.

Например, мы исследуем 40 систему счисления, и мы встретим ее закономерности в десятичной системе счисления. Таким образом, как циклические простые числа, полученные в десятичной си-стеме счисления, проявляют закономерность в 40й, так и циклические простые числа, полученные в 40й системе счисления проявляют закономерности в десятичной системе счисления.

Схожее верно и для 12 и 24 систем счисления. Несмотря на то, что многие системы счисления образуют одинаковые формулы, другие все же отличаются, например 12.

Итак, есть сами по себе циклические простые числа, они образуются в любой системе счисления, где изначальное простое число является full reptend.

Они могут быть взаимосвязаны с циклическими простыми числами в других системах счисления, при этом некоторые числа имеют связь только с системами счисления выше, другие же имеют и связь с системами счисления ниже, как в случае с 40 и 10 системами счисления.

Можно наблюдать схожую конструкцию для P = 5, есть повторяющиеся коэффициенты относительно первой системы счисления в группе. А в случае с P = 17 все становится намного сложней, видно, что шаги всегда равны base, base*2, base*4, однако их чередование меняется.

Хотя вывести непосредственно формулы сходу для меня оказалось тяжело, есть возможность показать, что от каждого простого числа можно образовывать циклические простые числа имеющие связи между собой в разных системами счисления.

Перечень наблюдений, требующих доказательства или опровержения

Возможно у вас создалась иллюзия что я профессиональный математик, имеющий математическое образование. На самом деле это не так. К моему сожалению мои познания в математике и в частности в Теории Чисел не так и глубоки, однако это не мешает мне испытывать большой трепет к этой дисциплине.

Я уверен что среди читателей Хабра есть профессиональные, настоящие математики. Я был бы безумно раз, если бы они помогли бы мне доказать мои наблюдения и оформить их в качестве теорем.

Разложение периодической дроби на бесконечное количество геометрических прогрессий
Наличие циклических простых чисел в каждой системе счисления, и то, что их потенциально бесконечное множество

Связи между циклическими простыми числами в разных системах счисления, отношение систем к одной группе

Возможность доказать или опровергнуть любые из моих гипотез крайне приветствуется!

Также интересна любая информация, касающаяся full reptend prime или циклических чисел.

Большая часть вычислений и визуализаций была сделана при помощи небольшого самодельного приложения. Его код далек от идеальности, но он помогает изучить закономерности визуально, все доступно на github. Там же можно найти английскую версию статьи.

Светлое будущее

У меня осталось несколько неосвещенных тем, связанных с full reptend prime. Однако их освещение требует дополнительного исследования и написания нового кода для визуализации.

Я надеюсь, что я смогу встретить хотя бы одного человека, кто серьезно заинтересован в этой теме, и тогда я продолжу это исследование с более серьезным отношением.

Большинство из описанных закономерностей, и в частности сами циклические простые и связи между ними в разных системах счисления были открыты мной в марте 2019 года, но работа\семья и другие исследования не позволяли добраться до публикации долгое время.

Недавно я закончил редактирование английской версии статьи, и теперь испытываю некоторое затруднение в том, чтобы опубликовать её на arxiv.org — мне нужно найти эндорсера. Я уже написал парочке потенциальных, однако они не отвечают. И одна из причин публикации этой статьи — возможность задать вопрос:

Дорогие Хабравчане, среди вас есть те кто публиковались на arxiv в категории Теории Чисел? Можете мне дать пожалуйста эндорсмент? Это потребует просто ввести 6-ти значный код при подачи моей публикации, я бы очень хотел поделиться этим открытием с миром.

Всем огромное спасибо за внимание! Надеюсь моя первая статья была не утомительной, впереди ещё несколько и не все о них будут о математике.