Найти подстроку в строке22.06.2021 11:17

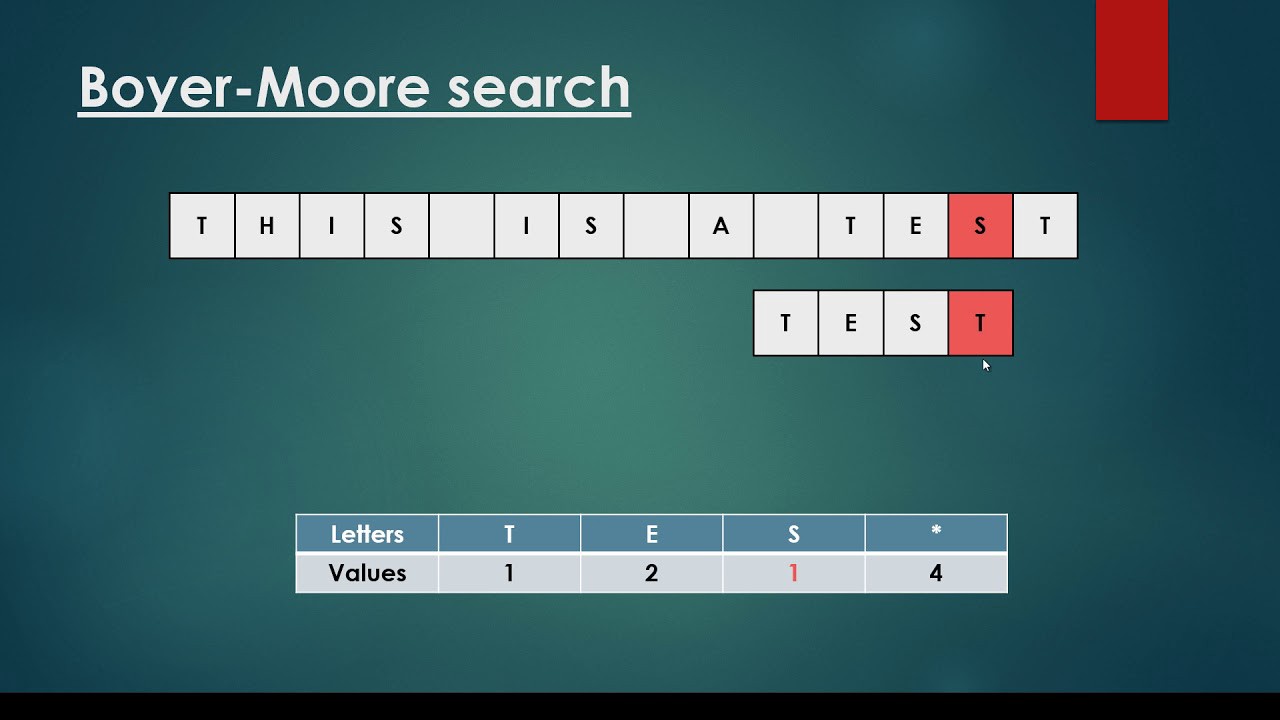
Алгоритм поиска строки Бойера — Мура — алгоритм общего назначения, предназначенный для поиска подстроки в строке.

Давайте попробуем найти вхождение подстроки в строку.

Наш исходный текст будет:

Text: somestring

И паттерн, который мы будем искать

Pattern: string

Давайте расставим индексы в нашем тексте, что бы видеть на каком индексе находится какая буква.

0 1 2 3 4 5 6 7 8 9
s o m e s t r i n g

Напишем метод, который определяет, находится ли шаблон в строке. Метод будет возвращать индекс откуда шаблон входит в строку.

int find (string text, string pattern){}

В нашем примере должно будет вернуться 4.

           0 1 2 3 4 5 6 7 8 9
text:      s o m e s t r i n g
pattern:           s t r i n g

Если ответ не найден, мы будем возвращать -1

int find (string text, string pattern) {   
int t = 0; создадим индекс для прохода по тексту.   
int last = pattern.length — 1; это индекс последнего элемента в шаблоне

Создадим цикл для прохода по тексту.

while (t < text.length — last)

Почему именно такое условие? Потому что если останется символов меньше чем длинна нашего паттерна, нам уже нет смысла проверять дальше. Наш паттерн точно не входит в строку.

В нашем примере:

last = 5 (Последний индекс паттерна string равен 5)

Длинна текста равна 10 (somestring)

Это значит что text.length — last = 10–5 = 5;

           0 1 2 3 4 5 6 7 8 9
text:      s o m e s t r i n g
pattern:           s t r i n g     

Можно заметить, что если мы стоим на 5 м индексе в строке, а 4й не подошел, то наш паттерн не входит в строку, например

            0 1 2 3 4 5 6 7 8 9
text:       s o m e X t r i n g                      
                    ^
pattern:            s t r i n g

Получится что длинна паттерна, больше чем длинна оставшейся строки.

На данный момент у нас есть код вида :

int find (string text, string pattern) {   
int t = 0;   
int last = pattern.length — 1;   
	while (t < text.length — last){  
	}
}

Теперьвведем переменную int p = 0, которая будет двигаться по нашему паттерну.

И запустим внутренний цикл

while( p <= last && text[ t + p ] == pattern[p] ){
}

p <= last — пока меньше или равно последнему индексу символа шаблона

text[ t + p ] = pattern[p] — пока очередной сивмол текста совпадает с символом в шаблоне.

Давайте детальнее разберем,  что значит text[ t + p ] = pattern[p]

Допустим мы в тексте стоим на индексе 4

              0 1 2 3 4 5 6 7 8 9
text:         s o m e s t r i n g                      
                      ^     
pattern:              s t r i n g

Получается t = 4, p = 0; text[ t + p ] = text[ 4 + 0 ] = s, pattern[0] = s, значит условие цикла выполняется.

Код на текущий момент:

int find (string text, string pattern) {   
int t = 0;   
int last = pattern.length — 1;   
	while (t < text.length — last) {      
  	int p = 0;      
    	while( p <= last && text[ t + p ] = pattren[p] ){         
      Если условие цикла выполняется, сдвигаем p вперед.         
      	p ++;      
      }         
      В результате если p == pattern.length 
      мы можем вернуть индекс на котором паттерн входит в текст.      
      	if (p == pattern.length){         
        	return t;      
      	}      
      В противном случае идем к следующему индексу в строке.      
      t ++;   
      }
   }

Получается мы имеем такой метод:

int find (string text, string pattern) {   
	int t = 0;   
	int last = pattern.length — 1;   
  	while (t < text.length — last) {      
    	int p = 0;      
      while( p <= last && text[ t + p ] == pattern[p] ) {
      	p ++;      
      }   
      if (p == pattern.length) {
      	return t;   
       }   
       t ++;   
     }   
   return — 1;
}

Как можно ускорить этот алгоритм? Какие есть варианты?

Представим что у нас в тексте есть символ, которого нет в паттерне.

text: some*string , то на сколько можно сдвигать паттерн?

А если есть повторяющиеся символы?

Например можно начать бежать с конца паттерна, то есть

text:     somestring               
               ^ 
pattern:  string               
               ^

Начинаем бежать с конца паттерна. Если символы не совпадают, на сколько можно сдвинуть паттерн?

Если символ из текста есть в нашем паттерне, то можно сразу сдвинуть до этого символа.

text:    somestring
pattern:     string

Сдвигаем на длину паттерна минус индекс символа на котором мы стоим в тексте.

То есть в данном случае

text: somestring           
           ^
pattern: string              
              ^

Когда мы начинаем бежать по паттерну с конца у нас pattern[i] = «g», а text[i] = «t»,

мы можем сдвинуть наш паттерн на pattern.length — индекс «t» в паттерне.

Индекс «t» в паттерне = 1, получается 5–1 = 4,  сдвигаем паттерн на 4 символа вперед.

text:         somestring                       
                       ^
pattern:      >>>>string                       
                       ^

Мы можем предварительно создать таблицу для нашего паттерна.

Посчитаем позицию каждого символа в паттерне, что бы знать на сколько сдвигаться.

Составляем таблицу смещений, для каждого символа алфавита. Я буду в примере использовать символ * что бы не расписывать весь алфавит.

Таблица смещений:
s 0
t 1
r 2
i 3
n 4
g 5
* -1

Давайте возьмем другой паттерн, что бы символы повторялись и было ясно, на сколько нужно двигать паттерн, если символы повторяются:

pattern: колокол
к 4
л 2 — если символ последний в строке, то оставляем его первый вход
м -1
н -1
о 5

Мы сдвигаем на последние вхождение символа, потому что если сдвигать на первое, то можно упустить часть входа паттерна в строку.

Попробуем реализовать эту часть алгоритма:

int[] createOffsetTable(string pattern) {   
	int[] offset = new int[128]; // количество символов зависит от 
  // алфавита с которым мы работаем   
  for (int i = 0; i < prefix.length; i++){
  	offset[i] = -1; // заполняем базовыми значениями   
  }   
  for (int i = 0; i < pattern.length; i++){
  	offset[pattern[i]] = i;   
  }   
  return offset;
}

Добавим таблицу смещений в алгоритм поиска, что мы написали выше:

int find (string text, string pattern) {   
	int[] offset = createOffsetTable(pattern);   
  int t = 0;   
  int last = pattern.length — 1;   
  while (t < text.length — last){
  	int p = last; // начнем двигаться с конца паттерна
    //Чуть чуть меняем условие цикла, 
    //так как теперь мы двигаемся с конца      
    while( p >= 0 && text[ t + p ] == pattern[p] ){
    	p — ;      
    }      
    if (p == -1){
    	return t;      
    }      
    t += last — offset[ text[ t + last ] ];   
  }   
  return — 1;
}

Почему t + last?  Смотрим на каком символе стоим в тексте и прибавляем длину шаблона. Если при поиске входа, какая то часть не совпала, то мы должны сдвинуться на символ текста в котором стоим + длинна шаблона.

Например:

Таблица смещений для колокол:
к = 4
л = 2
о = 5

Шаг 1:

         0 1 2 3 4 5 6 7 8 9 10
text:    а а к о л о л о к о л о к о л
pattern: к о л о к о л
last = 7; 
t += last — offset[text[t + last]]
t += last — offset[text[0 + 7]]
t += last — offset[‘о’]
t += 7–5 = 2;
t = 2;

Шаг 2:

         0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
text:    а а к о л о л о к о л о к о л
pattern: > > к о л о к о л
t = 2;
t += last — offset[text[t + last]]
t += last — offset[text[2 + 7]]
t += last — offset[‘о’]
t += 7–5 = 2;
t = 4;

Шаг 3:

         0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
text:    а а к о л о л о к о л о к о л
pattern: > > > > к о л о к о л
t = 4;
t += last — offset[text[t + last]]
t += last — offset[text[4 + 7]]
t += last — offset[‘о’]
t += 7–5 = 2;
t = 6;

Шаг 4:

         0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
text:    а а к о л о л о к о л о к о л
pattern: > > > > > > к о л о к о л
t = 6;
t += last — offset[text[t + last]]
t += last — offset[text[6 + 7]]
t += last — offset[‘о’]
t += 7–5 = 2;
t = 8;

Шаг 5:

         0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
text:    а а к о л о л о к о л о к о л
pattern: > > > > > > > > к о л о к о л

Совпадение найдено.

На этом разбор упрощенного алгоритма Бойера-Мура закончен.

Пока мы отталкивались только от крайних символов. Но возможно ли как то использовать информацию по уже пройденным символам?

Допустим есть строка

abcdadcd

Как составить таблицу смещений мы уже знаем. Теперь составим таблицу суффиксов.

Когда мы стоим на символе d, на сколько можно сдвинуть паттерн? Сдвигаем на на расстояние до ближайшего такого же символа. В примере ниже у нас есть 2 символа d с расстояниями 2 и 4. Мы выберем 2 потому что оно меньше.

            4   
          -----—    
          |   2   
          | ---   
          | | |
       abcdadcd       
       ^

Дальше рассмотрим суффикс cd. Для d мы уже записали 2.

       2
abcdadcd 
У нас есть только один суффикс cd, это значит что можно          
-- сдвинуться на 4 символа. 
Запишем для с = 4.   

     842
abcdadcd 
Далее dcd. dcd в тексте больше нигде не встречается.         
--- Двигаем на длину шаблона = 8

И для всех остальных символов пишем 8, потому что суффиксы не будут совпадать.

Теперь вернемся к нашему паттерну колокол.

колокол* В конце всегда будет *, еcли символ не совпал, сдвинем на 1.

              1
       колокол*       
              —       
             41
       колокол*      
             -—      
            441
       колокол*     
            --—     
           4441
       колокол*    
           ---—     
           4441
       колокол*    
           ----

Для окол мы тоже запишем 4. Потому что у нас префикс совпадает с суффиксом.

Попробуем написать код для этого

createSuffix(string pattern){   
	int[] suffix = new int[pattern.length + 1]; // +1 для символа звездочки   
  	for(int i = 0; i < pattern.length; i ++){
    	suffix[i] = pattern.length; // изначальное значение, 
      //длинна шаблона. на сколько сдвигать если нет совпадения суффиксов   
    }   
    suffix[pattern.length] = 1; // для звездочки ставим 1
    //Сначала создадим переменную, которая идет справа на лево.   
    for (int i = pattern.length — 1; i >= 0; i — ) {
    	for (int at = i; at < pattern.lenth; at ++){
      	string s = pattern.substring(at); // с какого символа берем подстроку

Например колокол с чем сравниваем?

        --— 
    колокол   
    	 --—  
      --- 
    ---
   ---

кол мы сравним с око, лок, оло, кол         

for (int j = at — 1; j >= 0; j — ) {
	string p = pattern.substring(j, s.length); // берем подстроку той же длинны
  //что и суффикс            
  if (p.equals(s)) { 
  	suffix[j] = at — i; 
    break;            
  }        
 }      
 }   
 }   
 return suffix;}

Существует более оптимальный алгоритм, но дальше индивидуально.

Какой код у нас есть на данный момент?

int[] createSuffix (string pattern) {   
	int[] suffix = new int[pattern.length + 1];   
  	for (int i = 0; i < pattern.length; i ++){
    	suffix[i] = pattern.length;   
    }   
    suffix[pattern.length] = 1;   
    for (int i = pattern.length — 1; i >=0; i — ){
    	for(int at = i; i < pattern.length; i ++){
      	string s = pattern.substring(at);         
        for (int j = at — 1; j >= 0; j — ){
        	string p = pattern.substring(j, s.length);
          if (p == s) {
          	suffix[i] = at — 1;
            at = pattern.length;
            break; 
          }        
        }      
      }  
    }   
    return suffix;
  }
  
int find(string text, string pattern) {   
	int[] offset = createOffset(pattern);   
  int[] suffix = createSuffix(pattern);   
  int t = 0;   
  int last = pattern.length — 1;   
  while (t < text.length — last) {
  	int p = last;      
    	while (p >= 0 && text[t + p] == pattern[p]) { 
      	p — ;    
      }      
    	if (p == -1) {
      	return t;
      }      
      t += Math.max (p — offset[text[t + p]], suffix[p + 1]);   
    }   
  return -1;
}

p — prefix[text[t + p]] — последний символ, который нашли и под него подстроить сдвиг нашего шаблона

suffix[p + 1] — значение суффикса для последнего элемента, который был сравнен.

И двигаем на максимальное значение, что бы двигаться максимально быстро.

На этом разбор алгоритма Бойера-Мура закончен. Спасибо за внимание! =)