Нахождение объектов на картинках01.04.2019 11:34

Мы занимаемся закупкой трафика из Adwords (рекламная площадка от Google). Одна из регулярных задач в этой области — создание новых баннеров. Тесты показывают, что баннеры теряют эффективность с течением времени, так как пользователи привыкают к баннеру; меняются сезоны и тренды. Кроме того, у нас есть цель захватить разные ниши аудитории, а узко таргетированные баннеры работают лучше.

В связи с выходом в новые страны остро встал вопрос локализации баннеров. Для каждого баннера необходимо создавать версии на разных языках и с разными валютами. Можно просить это делать дизайнеров, но эта ручная работа добавит дополнительную нагрузку на и без того дефицитный ресурс.

Это выглядит как задача, которую несложно автоматизировать. Для этого достаточно сделать программу, которая будет накладывать на болванку баннера локализованную цену на «ценник» и call to action (фразу типа «купить сейчас») на кнопку. Если печать текста на картинке реализовать достаточно просто, то определение положения, куда нужно его поставить — не всегда тривиально. Перчинки добавляет то, что кнопка бывает разных цветов, и немного отличается по форме.

Этому и посвящена статья: как найти указанный объект на картинке? Будут разобраны популярные методы; приведены области применения, особенности, плюсы и минусы. Приведенные методы можно применять и для других целей: разработки программ для камер слежения, автоматизации тестирования UI, и подобных. Описанные трудности можно встретить и в других задачах, а использованные приёмы использовать и для других целей. Например, Canny Edge Detector часто используется для предобработки изображений, а количество ключевых точек (keypoints) можно использовать для оценки визуальной «сложности» изображения.

Надеюсь, что описанные решения пополнят ваш арсенал инструментов и трюков для решения проблем.

Код приведён на Python 3.6 (репозиторий); требуется библиотека OpenCV. От читателя ожидается понимание основ линейной алгебры и computer vision.

Фокусироваться будем на нахождении самой кнопки. Про нахождение ценников будем помнить (так как нахождение прямоугольника можно решить и более простыми способами), но опустим, так как решение будет выглядеть аналогичным образом.

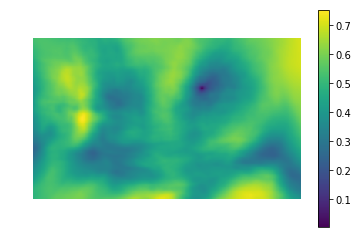
Первая же мысль, которая приходит в голову — почему бы просто не взять и найти на картинке регион, который наиболее похож на кнопку в терминах разницы цветов пикселей? Это и делает template matching — метод, основанный на нахождении места на изображении, наиболее похожем на шаблон. «Похожесть» изображения задается определенной метрикой. То есть, шаблон «накладывается» на изображение, и считается расхождение между изображением и и шаблоном. Положение шаблона, при котором это расхождение будет минимальным, и будет означать место искомого объекта.

В качестве метрики можно использовать разные варианты, например — сумма квадратов разниц между шаблоном и картинкой (sum of squared differences, SSD), или использовать кросс-корреляцию (cross-correlation, CCORR). Пусть f и g — изображение и шаблон размерами (k, l) и (m, n) соответственно (каналы цвета пока будем игнорировать); i, j — позиция на изображении, к которой мы «приложили» шаблон.

$SSD_{i,j}=\sum_{a=0..m, b=0..n}{(f_{i+a, j+b} - g_{a, b})^2}$

$CCORR_{i,j}=\sum_{a=0..m, b=0..n}{(f_{i+a, j+b} \cdot g_{a, b})^2}$

Попробуем применить разницу квадратов для нахождения котёнка

На картинке

(картинка взята с ресурса PETA Caring for Cats).

Левая картинка — значения метрики похожести места на картинке на шаблон (т.е. значения SSD для разных i, j). Темная область — это и есть место, где разница минимальна. Это и есть указатель на место, которое наиболее похоже на шаблон — на правой картинке это место обведено.

Кросс-корреляция на самом деле является сверткой двух изображений. Свёртки можно реализовать быстро, используя быстрое преобразование Фурье. Согласно теореме о свёртке, после преобразования Фурье свёртка превращается в простое поэлементное умножение:

$CCORR_{i,j}=f \circledast g = IFFT(FFT(f \circledast g)) = IFFT(FFT(f) \cdot FFT(g))$

Где $\circledast$ — оператор свёртки. Таким образом мы можем быстро посчитать кросс-корреляцию. Это даёт общую сложность O (kllog (kl)+mnlog (mn)), против O (klmn) при реализации «в лоб». Квадрат разницы также можно реализовать с помощью свёртки, так как после раскрытия скобок он превратится в разницу между суммой квадратов значений пикселей изображения и кросс-корреляции:

$SSD_{i,j}=\sum_{a=0..m, b=0..n}{(f_{i+a, j+b} - g_{a, b})^2} =$

$=\sum_{a=0..m, b=0..n}{f_{i+a, j+b}^2 - 2 f_{i+a, j+b} g_{a, b} + g_{a, b}^2} =$

$=\sum_{a=0..m, b=0..n}{f_{i+a, j+b}^2 + g_{a, b}^2} - 2CCOR_{i,j}$

Детали можно посмотреть в этой презентации.

Перейдём к реализации. К счастью, коллеги из нижненовгородского отдела Intel позаботились о нас, создав библиотеку OpenCV, в ней уже реализован поиск шаблона с помощью метода matchTemplate (кстати используется именно реализация через FFT, хотя в документации это нигде не упоминается), использующий разные метрики расхождений:

CV_TM_SQDIFF — сумма квадратов разниц значений пикселей
CV_TM_SQDIFF_NORMED — сумма квадрат разниц цветов, отнормированная в диапазон 0…1.
CV_TM_CCORR — сумма поэлементных произведений шаблона и сегмента картинки
CV_TM_CCORR_NORMED — сумма поэлементных произведений, отнормированное в диапазон -1…1.
CV_TM_CCOEFF — кросс-коррелация изображений без среднего
CV_TM_CCOEFF_NORMED — кросс-корреляция между изображениями без среднего, отнормированная в -1…1 (корреляция Пирсона)

Применим их для поиска котёнка:

Видно, что только TM_CCORR не справился со своей задачей. Это вполне объяснимо: так как он представляет собой скалярное произведение, то наибольшее значение этой метрики будет при сравнении шаблона с белым прямоугольником.

Можно заметить, что эти метрики требуют попиксельного соответствия шаблона в искомом изображении. Любое отклонение гаммы, света или размера приведут к тому, что методы не будут работать. Напомню, что это именно наш случай: кнопки могут быть разного размера и разного цвета.

Проблему разного цвета и света можно решить применив фильтр нахождения граней (edge detection filter). Этот метод оставляет лишь информацию о том, в каком месте изображения находились резкие перепады цвета. Примененим Canny Edge Detector (его подробнее разберём чуть дальше) к кнопкам разного цвета и яркости. Слева приведены исходные баннеры, а справа — результат применения фильтра Canny.

В нашей случае, также существует проблема разных размеров, однако она уже была решена. Лог-полярная трансформация преобразует картинку в пространство, в котором изменение масштаба и поворот будут проявляться как смещение. Используя эту трансформацию, мы можем восстановить масштаб и угол. После этого, отмасштабировав и повернув шаблон, можно найти и позицию шаблона на исходной картинке. Во всей этой процедуре также можно использовать FFT, как описано в статье An FFT-Based Technique for Translation, Rotation, and Scale-Invariant Image Registration. В литературе рассматривается случай, когда по горизонтали и вертикали шаблон изменяется пропорционально, и при этом коэффициент масштаба варьируется в небольших пределах (2.0… 0.8). К сожалению, изменение размеров кнопки может быть бо́льшим и непропорциональным, что может привести к некорректному результату.

Применим полученную конструкцию (фильтр Canny, восстановление только масштаба через лог-полярную трансформацию, получение положения через нахождения места с минимальным квадратичным расхождением), для нахождения кнопки на трех картинках. В качестве шаблона будем использовать большую желтую кнопку:

При этом на баннерах кнопки будут разных типов, цветов и размеров:

В случае с изменением размера кнопки метод сработал некорректно. Это связано с тем, что метод предполагает изменение размеров кнопок в одинаковое количество раз и по горизонтали, и по вертикали. Однако, это не всегда так. На правой картинке размер кнопки по вертикали не изменился, а по горизонтали — уменьшился сильно. При слишком большом изменении размера искажения, вызванные логполярным преобразованием, делают поиск нестабильным. В связи с этим метод не смог обнаружить кнопку в третьем случае.

Можно попробовать другой подход: давайте вместо того, чтобы искать кнопку целиком, найдём её типичные части, например, углы кнопки, или элементы бордюра (по контуру кнопки есть декоративная обводка). Кажется, что найти углы и бордюр проще, так как это мелкие (а значит, простые) объекты. То, что лежит между четырёх углов и бордюра — и будет кнопкой. Класс методов нахождения ключевых точек называется «keypoint detection», а алгоритмы сравнения и поиска картинок с помощью ключевых точек — «keypoint matching». Поиск шаблона на картинке сводится к применению алгоритма обнаружения ключевых точек к шаблону и картинке, и сопоставлению ключевых точек шаблона и картинки.

Обычно «ключевые точки» находят автоматически, находя пиксели, окружение которых которых обладает определёнными свойствами. Было придумано множество способов и критериев их нахождения. Все эти алгоритмы являются эвристиками, которые находят какие-то характерные элементы изображения, как правило — углы или резкие перепады цвета. Хороший детектор должен работать быстро, и быть устойчивым к трансформациям картинки (при изменении картинки ключевые точки не должны переставать находиться/двигаться).

Harris corner detector

Одним из самых базовых алгоритмов считается Harris corner detector. Для картинки (тут и дальше мы считаем, что оперируем «интенсивностью» — изображением, переведенной в grayscale) он пытается найти точки, в окрестностях которых перепады интенсивности больше определенного порога. Алгоритм выглядит так:

От интенсивности находятся производные по оси X и Y ( и соответственно). Их можно найти, например, применив фильтр Собеля.
Для пикселя считаем квадрат , квадрат и произведения и . Некоторые источники обозначают их как $I_{xx}$ , $I_{xy}$ и $I_{xy}$ — что не добавляет понятности, так как можно подумать, что это вторые производные интенсивности (а это не так).
Для каждого пикселя считаем суммы в некой окрестности (больше 1 пикселя) w следующие характеристики:

$A = \sum_{x,y}{w(x,y)I_xI_x}$

$B = \sum_{x,y}{w(x,y)I_xI_y}$

$C = \sum_{x,y}{w(x,y)I_yI_y}$

Как и в Template Detection, эту процедуру для больших окон можно провести эффективно, если использовать теорему о свертке.
Для каждого пикселя посчитать значение $^\star$ эвристики R

Значение подбирается эмпирически в диапазоне [0.04, 0.06] Если у какого-то пикселя больше определенного порога, то окрестность этого пикселя содержит угол, и мы отмечаем его как ключевую точку.
Предыдущая формула может создавать кластеры лежащих рядом друг с другом ключевых точек, в таком случае стоит их убрать. Это можно сделать проверив для каждой точки является ли у неё значение максимальным среди непосредственных соседей. Если нет — то ключевая точка отфильтровывается. Эта процедура называется non-maximum suppression.

$\star$ Формула $ R $ выбрана так неспроста. $ A, B, C $ — компоненты структурного тензора — матрицы, описывающую поведение градиента в окрестности:

$H = \begin{pmatrix} A & C \\ C & B \end{pmatrix}$

Эта матрица многими свойствами и формой похожа на матрицу ковариации. Например, они обе положительно полуопределённые матрицы, но этим сходство не ограничивается. Напомню, что у матрицы ковариации есть геометрическая интерпретация. Собственные вектора матрицы ковариации указывают на направления наибольшей дисперсии исходных данных (на которых ковариация была посчитана), а собственные числа — на разброс вдоль оси:

Картинка взята из http://www.visiondummy.com/2014/04/geometric-interpretation-covariance-matrix/

Точно так же ведут себя и собственные числа структурного тензора: они описывают разброс градиентов. На ровной поверхности собственные числа структурного тензора будут маленькими (потому что разброс самих градиентов будет маленьким). Собственные числа структурного тензора, построенного на кусочке картинки с гранью, будут сильно различаться: одно число будет большим (и соответствовать собственному вектору, направленному перпендикулярно грани), а второе — маленьким. На тензоре угла оба собственных числа будут большие. Исходя из этого, мы можем построить эвристику ( $\lambda_1 , \lambda_2$ — собственные числа структурного тензора).

$R = \lambda_1\lambda_2 - k(\lambda_1 + \lambda_2)^2$

Значение этой эвристики будет большое, когда оба собственных числа — большие.

Сумма собственных чисел — это след матрицы, который можно рассчитать как сумму элементов на диагонали (а если взглянуть на формулы A и B, то станет понятно, что это еще и сумма квадратов длин градиентов в области):

$\lambda_1 + \lambda_2 = Tr(H) = A + B$

Произведение собственных чисел — определитель матрицы, который в случае 2×2 тоже легко выписать:

$\lambda_1 \lambda_2 = Det(H) = AB - C^2$

Таким образом, мы можем эффективно посчитать $ R $ , выразив её в терминах компонентов структурного тензора.

FAST

Метод Харриса хорош, но существует множество альтернатив ему. Рассматривать так же подробно, как метод выше, все не будем, упомянем лишь несколько популярных, чтобы показать интересные приёмы и сравнить их в действии.

Пиксели, проверяемые алгоритмом FAST

Альтернатива методу Харриса — FAST. Как подсказывает название, FAST работает гораздо быстрее вышеописанного метода. Этот алгоритм пытается найти точки, которые лежат на краях и углах объектах, т.е. в местах перепада контраста. Их нахождение происходит следующим образом: FAST строит вокруг пикселя-кандидата окружность радиуса R, и проверяет, есть ли на ней непрерывный отрезок из пикселей длины t, который темнее (или светлее) пикселя-кандидата на K единиц. Если это условие выполняется, то пиксель считается «ключевой точкой». При определённых t мы можем реализовать эту эвристику эффективно, добавив несколько предварительных проверок, которые будут отсекать пиксели гарантированно не являющиеся углами. Например, при $ R=3 $ и $ t=12 $ , достаточно проверить, есть ли среди 4 крайних пикселей 3 последовательных, которые строго темнее/светлее центра на K (на картинке — 1, 5, 9, 13). Это условие позволяет эффективно отсечь кандидатов, точно не являющихся ключевыми точками.

SIFT

Оба предыдущих алгоритма не устойчивы к изменениям размера картинки. Они не позволяют найти шаблон на картинке, если масштаб объекта был изменён. SIFT (Scale-invariant feature transform) предлагает решение этой проблемы. Возьмем изображение, из которого извлекаем ключевые точки, и начнём постепенно уменьшать его размер с каким-то небольшим шагом, и для каждого варианта масштаба будем находить ключевые точки. Масштабирование — тяжелая процедура, но уменьшение в 2/4/8/… раз можно провести эффективно, пропуская пиксели (в SIFT эти кратные масштабы называются «октавами»). Промежуточные масштабы можно аппроксимировать, применяя к картинке гауссовский блюр с разным размером ядра. Как мы уже описали выше, это можно сделать вычислительно эффективно. Результат будет похож на то, как если бы мы сначала уменьшили картинку, а потом увеличили ее до исходного размера — мелкие детали теряются, изображение становится «замыленным».

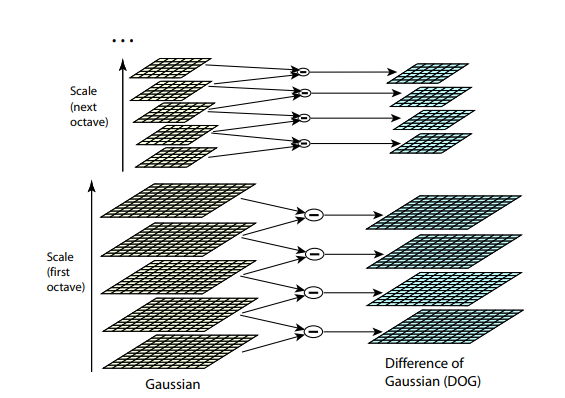
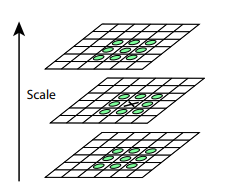
После этой процедуры посчитаем разницу между соседними масштабами. Большие (по модулю) значения в этой разнице получатся, если какая-то мелкая деталь перестает быть видна на следующем уровне масштаба, или, наоборот, следующий уровень масштаба начинает захватывает какую-то деталь, которая на предыдущем не была видна. Этот прием называется DoG, Difference of Gaussian. Можно считать, что большое значение в этой разнице уже является сигналом того, что в этом месте на изображении есть что-то интересное. Но нас интересует тот масштаб, для которого эта ключевая точка будет наиболее выразительной. Для этого будем считать ключевой точкой не только точку, которая отличается от своего окружения, но и отличается сильнее всего среди разных масштабов изображений. Другими словами, выбирать ключевую точку мы будем не только в пространстве X и Y, а в пространстве $ (X, Y, Scale) $ . В SIFT это делается путём нахождения точек в DoG (Difference of Gaussians), которые являются локальными максимумами или минимумами в $ 3x3x3 $ кубе пространства вокруг неё:

Алгоритмы нахождения ключевых точек и построения дескрипторов SIFT и SURF запатентованы. То есть, для их коммерческого использования необходимо получать лицензию. Именно поэтому они недоступны из основного пакета opencv, а только из отдельного пакет opencv_contrib. Однако, пока что наше исследование носит исключительно академический характер, поэтому ничто не мешает поучаствовать SIFT в сравнении.

Дескрипторы

Попробуем применить какой-нибудь детектор (например, Харриса) к шаблону и картинке.

После нахождения ключевых точек на картинке и шаблоне надо как-то сопоставить их друг с другом. Напомню, что мы пока извлекли только положения ключевых точек. То, что обозначает эта точка (например, в какую сторону направлен найденный угол), мы пока не определили. А такое описание может помочь при сопоставлении точек изображения и шаблона друг с другом. Часть точек шаблона на картинке может быть сдвинута искажениями, закрыта другими объектами, поэтому опираться исключительно на положение точек относительно друг друга кажется ненадежным. Поэтому давайте для каждой ключевой точки возьмём её окрестность чтобы построить некое описание (дескриптор), которое потом позволит взять пару точек (одну точку из шаблона, одну из картинки), и сравнить их схожесть.

BRIEF

Если мы сделаем дескриптор в виде бинарного массива (т.е. массив из 0 и 1), то мы их сможем сравнивать крайне эффективно, сделав XOR двух дескрипторов, и посчитать количество единичек в результате. Как составить такой вектор? Например, мы можем выбрать N пар точек в окрестности ключевой точки. Затем, для i-й пары проверить, является ли первая точка ярче второй, и если да — то в i-ю позицию дескриптора записать 1. Таким образом мы можем составить массив длины N. Если мы будем выбирать в качестве одной из точек всех пар какую-то одну точку в окрестности (например, центр окрестности — саму ключевую точку), то такой дескриптор будет неустойчивым к шуму: достаточно немного поменяться яркости всего одного пикселя, чтобы весь дескриптор «поехал». Исследователи обнаружили, что достаточно эффективно выбрать точки случайно (из нормального распределения с центром в ключевой точке). Это положено в основу алгоритма BRIEF.

Часть рассмотренных авторами методов генераций пар. Каждый отрезок символизирует пару сгенерированных точек. Авторы обнаружили, что вариант GII работает чуть лучше остальных вариантов.

После того, как мы выбрали пары, их стоит зафиксировать (т.е. пары генерировать не при каждом запуске расчёта дескриптора, а сгенерировать один раз, и запомнить). В реализации от OpenCV эти пары и вовсе сгенерированы заранее и захардкожены.

Дескриптор SIFT

SIFT также может эффективно считать дескрипторы, используя результаты применения гауссового размытия на разных октавах на картинке. Для расчёта дескриптора SIFT выбирает регион 16×16 вокруг ключевой точки, и разбивает его на блоки 4×4 пикселя. Для каждого пикселя считается градиент (мы оперируем в том же масштабе и октаве, в котором была найдена ключевая точка). Градиенты в каждом блоке распределяются на 8 групп по направлению (вверх, вверх-вправо, вправо, и т.д.). В каждой группе длины градиентов складываются — получается 8 чисел, которые можно представить как вектор, описывающий направление градиентов в блоке. Этот вектор нормируется для устойчивости к изменению яркости. Так, для каждого блока рассчитывается 8-мерный вектор единичной длины. Эти вектора конкатенируются в один большой дескриптор длины 128 (в окрестности 4×4 = 16 блоков, в каждом по 8 значений). Для сравнения дескрипторов используется Евклидово расстояние.

Сравнение

Находя пары наиболее подходящих друг к другу ключевых точек (например — жадно составляя пары, начиная с самых похожих по дескрипторам), мы наконец-таки сможем сравнить шаблон и картинку:

Котик нашелся —, но тут у нас имеется попиксельное соответствие между шаблоном и фрагментом картинки. А что будет в случае кнопки?

Предположим, перед нами прямоугольная кнопка. Если ключевая точка расположена на углу, то три четверти локали точки будет именно то, что лежит за пределами кнопки. А то, что лежит за пределами кнопки, сильно меняется от картинки к картинке, в зависимости от того, поверх чего расположена кнопка. Какая доля дескриптора будет оставаться постоянной при изменении фона? В дескрипторе BRIEF, так как координаты пары выбираются в локали случайно и независимо, бит дескриптора будет оставаться постоянным только в случае, когда обе точки лежат на кнопке. Другими словами, в BRIEF всего 1/16 дескриптора не будет меняться. В SIFT ситуация чуть лучше — из-за блочной структуры ¼ дескриптора меняться не будет.

В связи с этим дальше будем использовать дескриптор SIFT.

Сравнение детекторов

Теперь применим все полученные знания для решения нашей задачи. В нашем случае требования к детектору ключевых точек достаточно: инвариантность к изменению размера нам ни к чему, равно как и крайне высокая производительность. Сравним все три детектора.

SIFT нашел крайне мало ключевых точек на кнопке. Это объяснимо — кнопка представляет собой достаточно небольшой и плоский объект, и изменение масштаба не помогает найти ключевые точки.

Также, ни один детектор не справился с третьим случаем. Это объяснимо и ожидаемо. Обычно вышеописанные методы применяют для того, чтобы найти объект из шаблона на снимке, на котором он может быть частично скрыт, быть повернут, или немного искажен. В нашем случае мы хотим найти не точно такой же объект, а объект, достаточно похожий на шаблон (кнопку) . Это немного другая задача. Так, изменение самой формы кнопки (например, радиуса скругления углов, или толщины рамки точек) меняет ключевые точки в них, и их дескрипторы. Кроме того, ключевые точки будут находиться на углу кнопки. Из-за положения на краю точки будут неустойчивы: на их точное расположение и дескрипторы влияет то, что нарисовано рядом с кнопкой.

Вывод — метод хорош, и корректно отрабатывает ситуации, когда искомый объект повернут, его размер изменен, или объект частично скрыт (что хорошо для поиска сложных объектов, или ценника, например). Однако, если на объекте мало точек, за которые можно «зацепиться», или форма объекта меняется слишком сильно, то ключевые точки и их на шаблоне и изображении могут не совпасть. Также, фон с большим количеством мелких деталей может сместить «ключевые точки» или изменить их дескрипторы.

Мы можем придумать матчинг, который бы использовал координаты ключевых точек. Вместо того, чтобы искать пары точек на шаблоне и картинке, окрестность которых похожа, можно искать такие наборы точек, взаимоположение ключевых точек на шаблоне и картинке будут похожи. В общем случае это достаточно сложная (и вычислительно, и с точки зрения программирования) задача, особенно в ситуации, когда некоторые точки могут быть сдвинуты или отсутствовать. Но, учитывая, что у нас ключевые точки — углы, нам достаточно найти такие группы, которые будут примерно образовывать прямоугольник нужных пропорций, и внутри которого не будет ключевых точек. Постепенно мы подходим к следующему методу:

Обычно кнопка — это какой-то прямоугольный объект (иногда — со скруглёнными углами), стороны которого параллельны осям координат. Тогда давайте попробуем выделить зоны перепады контраста (грани/edges), и среди них найдем грани, очертания которых похожи на контур нужного нам объекта. Этот метод называется contour detection.

Edge detection

В отличии от keypoint detection, нам интересны не только ключевые точки-углы, но и рёбра. Однако, основные идеи мы можем взять оттуда. Сгладим изображение Гауссовым фильтром, и как в Harris corner detector. Затем посчитаем производные интенсивности $ I_x $ и $ I_y $ . Так как нам не нужно отличать углы от ребер, то не надо считать структурный тензор — достаточно посчитать силу градиента: $ I_l = I_x^2+I_y^2 $ (кстати, это корень из $ Tr(H) $ , или из суммы диагонали структурного тензора). После этого, оставим только пиксели, которые являются локальными максимумами в терминах $ I_l $ (используя уже расмотренный non-maximum suppression), но в качестве локали будем выбирать не 8 соседних пикселей, а те пиксели из этих 8, в сторону которого направлен I, и с противоположной стороны:

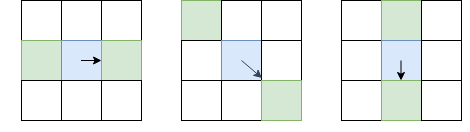
Синим отмечен рассматриваемый пиксель, стрелка — направление I. Зелёные пиксели — те, которые будут учитываться при non-maximum suppression.

Такой необычный выбор пикселей для сравнения обусловлен тем, что мы не хотим делать разрывы в границе. В левой картинке грань проходит сверху вниз, и так как non-maximum suppression не будет проводить сравнения интенсивности с пикселями выше и ниже синего, мы получим непрерывную грань.

Очевидно, одного non-maximum suppression недостаточно, и надо применить какую-то фильтрацию, чтобы убрать ребра со слишком низким Il. Для этого применим приём «double thresholding»: уберем все пиксели с Il, силой градиента, ниже порога Low, все пиксели выше порога High назначим «сильными ребрами». Пиксели, у которых сила градиента лежит между Low и High, назовём «слабыми ребрами», оставим только если они соединены с «сильными ребрами»:

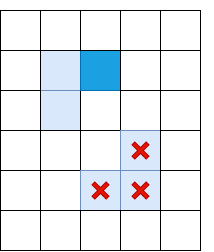
Светло-синим отмечены «слабые ребра», тёмно-синим — сильные. Ребра в нижней части отсеиваются, так как они не соеденены ни с одним сильным ребром.

Мы только что описали Canny Edge Detector. Он крайне широко применяется и по сей день в качестве простой и быстрой процедуры, позволяющей найти контуры объектов.

Border tracking

Следующее действие — среди карты с найденными гранями выделить контуры. Найдем связанные компоненты (острова смежных пикселей, прошедших все проверки), и проверим каждый из них, насколько он похож на кнопку. После применения non-maximum suppression в Canny, у нас есть гарантии того, что ребра будут получаться толщиной в один пиксель, но давайте на будем на нее опираться. Для каждого пикселя, который был отнесен к грани, и рядом с которым есть пиксель не-грань, отнесем к «бордюру». Перемещаясь от одного пикселя бордюра к другому, мы либо придём обратно в тот же пиксель (и тогда мы нашли контур), либо в тупик (тогда можно попробовать вернуться назад, если где-то по пути была развилка):

Полный алгоритм border tracking, учитывающий разные краевые случаи (например, когда объект с толстой гранью сгенерировал два контура, внутренний и внешний), описан тут. После применения этого алгоритма у нас останется набор контуров, которые потенциально могут быть кнопками.

Фильтрация контуров

Как узнать, что наш контур — кнопка? Для прямоугольников и многоугольников есть отличный > метод, основанный на упрощении контура. Достаточно постепенно «схлопывать» ребра, если они находятся почти на одной прямой, а затем посчитать количество оставшихся ребер, и проверить углы между ними. К сожалению, для нашего случая эти методы не подходят — наш прямоугольник имеет скругленные углы. Также, есть contour matching для фигур, имеющих сложную геометрию —, но это тоже не про нас, так как у нас всего лишь прямоугольник (в статье приводятся примеры с контуром человека). Поэтому лучше сделать фильтр, основанный на свойства самой фигуры. Мы знаем, что:

Кнопка достаточно большая (площадь больше 100 пикселей)
Стороны параллельны осям координат
Отношение площади фигуры к площади ограничивающего прямоугольника должна быть достаточно близка к единице. Мы устанавливаем порог в 0.8, так как кнопка — прямоугольник со сторонами параллельными осям координат, и недостающие 20% — это и есть скругленные углы.

Кроме того, по опыту применения детекторов ключевых точек мы помним, что могут быть проблемы с ситуациями, когда под кнопкой лежит контрастный объект. Поэтому после применения Canny размоем грани, чтобы закрыть мелкие дырки, которые могли возникнуть из-за таких объектов.

Применим получившийся подход:

Применение Canny filter (2 картинка) нашло нужные очертания, но из-за сложной формы кнопки и градиента нашлось сразу много контуров, и из-за non-max suppression некоторые из них не были замкнуты. Применение размытия (3 картинка) исправило проблему.

Запустим в получившейся картинке поиск контуров. Покрасим контуры, прошедшие проверки, красным цветом. Если таких несколько, то нам нужно выбрать среди них наиболее удачный вариант. Выберем контур наибольшей площади, и покрасим его в зелёный цвет.

| | | |

Получившаяся конструкция нашла кнопки на тестовых изображениях. Прогон на всех баннерах показал, что изредка (1 случай из ~20) она вместо кнопки выделяет прямоугольные плашки iOS Appstore и Google Apps, или другие прямоугольные объекты (чехлы телефонов). Поэтому добавив возможность ручного указания положения на тот редкий случай неверного определения, мы реализовали этот вариант в инструменте локализации.

Подведем итоги. «Классический» CV без deep learning по-прежнему работает, и на его основе можно решить задачи. Они неприхотливы и не требуют большого количества размеченных данных, мощного железа, и их проще отлаживать. Однако, они вводят дополнительные предположения, и поэтому с их помощью не каждую задачу можно решить эффективно.

Template Matching — самый простой способ, основывается на нахождении места в изображении, наиболее похожем (по какой-то простой метрике) на шаблон. Эффективен при попиксельном совпадении. Можно сделать устойчивым к поворотам и небольшим изменениям размеров, но при больших изменениях может работать некорректно.
Keypoint detection/matching — находим ключевые точки, сопоставляем точки изображения и шаблона. Детекторы устойчивы к поворотам, изменениям масштаба (в&
© Habrahabr.ru