n-Queens Completion Problem — линейный алгоритм решения
EricGrig
Предисловие
Я хотел бы начать предисловие со слов благодарности двум замечательным программистам из Одессы: Андрею Киперу (Lohica) и Тимуру Гиоргадзе (Luxoft), за независимую проверку полученных мною результатов, на начальном этапе исследования.
1. Статья «Linear algorithm for solution n-Queens Completion Problem» была опубликована в (arXiv.org) в начале первого дня 2020 года. Изначально статья была написана на русском, поэтому здесь представлено базовое изложение, а там — перевод.
2. Данная задача, и некоторые другие из множества NP-Complete (задача выполнимости булевых формул (3-SAT), задача о поиске максимальной клики, или клики заданного размера …) в разное время, входили в сферу моих интересов. Я искал алгоритмическое решение на основе различных вычислительных экспериментов, но конкретного успеха не было. Это было похоже на то, как человек пытается научиться подтянутся на турнике на одной руке. Результата нет, но каждый раз появляется надежда, что скоро все получится. Последний раз я решил, что следует подольше остановиться на задаче n-Queens Completion (как одной из представителей семейства) и попытаться что-то сделать. Здесь уместно вспомнить замечательный Одесский анекдот: «В переполненном автобусе, который вечером по ухабистой дороге возвращается в пригород, раздается голос женщины — Мужчина, если уж полностью на меня легли, так сделайте хоть что-нибудь».
3. Исследование длилось достаточно долго — почти полтора года. С одной стороны, это связано с тем, что в процессе исследования, рассматривались и другие задачи, с другой — по ходу решения были сложные вопросы, без ответа на которые не удалось бы идти вперед. Перечислю некоторые из них:
— в матрице решения n строк, в какой последовательности следует выбирать индекс строки, если число возможностей для такого выбора составляет n!
— когда сделан выбор строки, какую из оставшихся свободных позиций в этой строке следует выбрать, ведь число возможностей такого отбора настолько большое, что его можно считать «близким родственником» бесконечности (например, число возможных способов выбора свободной позиции во всех строках для шахматной доски размера 100×100 составляет примерно 10124)
— совместно, эти два показателя формируют пространство состояния (пространство выбора). Казалось бы, огромные возможности, можно выбирать какую хочешь. Но за каждым конкретным выбором на каждом шаге, скрывается другая проблема — ограничение возможностей выбора во всех последующих шагах. Причем, это особо чувствительно на последних этапах решения задачи. Можно сказать, что матрица решения «злопамятна». Все «неосознанные ошибки», которые вы допускаете, совершая выбор на предыдущих этапах, «накапливаются», и под конец решения это проявляется в том, что в тех строках, где вы должны расположить ферзь, не остается свободных позиций и ветвь поиска заходит в тупик. Здесь как у Жванецкого: «одно неверное движение, и вы беременны».
— когда ветвь поиска решения заходит в тупик, у нас есть возможность возврата назад, на какую-то из предыдущих позиций (Back Tracking), чтобы с этой позиции снова начать формирование ветви поиска решения. Это естественное «свойство» не детерминированных задач. Вопрос состоит в том, на какой из предыдущих уровней следует возвращаться. Это такая же открытая проблема, как и вопрос выбора индекса строки, или выбора свободной позиции в этой строке.
— наконец, следует отметить проблему, связанную со скоростью работы алгоритма. Было бы грустно, если бы не было цели создавать быстро работающие алгоритмы. В процессе моделирования не удалось разработать один алгоритм, который быстро и эффективно работал бы на всех участках решения задачи. Пришлось разработать три алгоритма. Они передают результаты один-другому, как эстафетную палочку. Один из них работает очень быстро, но грубо, другой — наоборот, работает медленно, но эффективно. Каждый из них работает в «зоне своей ответственности».
4. Изначально, цель исследования состояла только в том, чтобы найти хоть какое-то решение. Пришлось много с чем разобраться, прежде чем был разработан первый вариант решения. На это потребовалось больше четырех месяцев. Можно было на этом остановиться, цель достигнута — ну и ладно. Но мне показалось, что не все возможности алгоритмического решения данной проблемы исчерпаны. Естественно, появилось желание усовершенствовать разработанный алгоритм таким образом, чтобы по временной сложности алгоритм был линейным-O (n). Когда такое линейное решение было найдено, появилось «еще одно желание» — уменьшить число случаев применения процедуры Back Tracking (BT) при формировании ветви поиска решения. Это было «наглое» желание перевести задачу из не детерминированной, в условно детерминированную (насколько это возможно). На это потребовалось много времени, но цель была достигнута, например, в интервале значений размера шахматной доски n = (320, …, 22500), число случаев, когда процедура BT ни разу не используется — превышает 50%. Получается, что в 50% случаев запуска программы, алгоритм «целенаправленно» формирует решение, ни разу не «спотыкаясь». (Помня сказку про золотую рыбку, я на этих двух желаниях и остановился…)
5. Сравнивая публикации, с которыми мне удалось познакомиться в процессе исследования, я пришел к выводу, что данную задачу, и другие задачи подобного рода не удастся решить на основе строгого математического подхода, т. е. только на основе определений, формулировке лемм и доказательстве теорем. Об этом в статье есть «философское замечание». Я уверен, что многие задачи из множества NP-Complete удастся решить только на основе алгоритмической математики с применение компьютерного моделирования. Такой вывод не означает ограничение математики, наоборот — это означает расширение возможностей математики, через развитие методов алгоритмической математики. Для каждого семейства задач нужно использовать свой адекватный математический подход. (Зачем поручать аспиранту решать задачу из семейства NP-Complete без применения методов алгоритмической математики и компьютерного моделирования, если известно, что из такой затеи ничего толком не выйдет).
6. Любой алгоритм (программа) имеет простое свойство — или работает, или нет! Я хочу обратиться к тем членам нашего Хабро-Сообщества, у которых в зоне доступности есть компьютер с установленным Матлабом. Хочу попросить Вас протестировать работу рассматриваемого алгоритма решения n-Queens Completion Problem. Для этого потребуется всего 5–10 минут. Чтобы протестировать алгоритм, нужно выполнить несколько простых шагов:
-генерировать случайную композицию из k ферзей и проверить правильность этой композиции.
-на основе предложенного алгоритма решения комплектовать данную композицию до полного решения. Либо программа должна принять решение, что данная композиция не имеет решения.
-проверить правильность решения, полученного в результате комплектации.
Вам не придется писать какой либо код для такого тестирования. Кроме основной программы, я подготовил еще две программы на языке Матлаб:
1. Generarion_k_Queens_Composition — генерация случайной композиции размера k для произвольной шахматной доски размера n x n
2.Completion_k_Queens_Composition.m — комплектация произвольной композиции до полного решения, либо принятие решение, что данная композиция не имеет решения (основная программа).
3.Validation_n_Queens_Solution.m — проверка правильности решения n-Queens Problem, либо правильности композиции из k ферзей.
Они работают очень быстро. Например, для шахматной доски, размер которой составляет 1000×1000 клеток, общее время, которое в среднем необходимо для генерации произвольной композиции (0.0015 с.), комплектации данной композиции (0.0622 с.), и проверки правильности полученного решения (0.0003 с.) не превышает 0.1 секунды. (исключая время, которое необходимо для загрузки данных, или сохранения полученных результатов)
Напишите мне (ericgrig@gmail.com), если у Вас есть возможность оказать помощь другу, я сразу вышлю Вам эти три программы. Я буду благодарен всем коллегам, которые смогут объективно провести тестирование алгоритма, и выскажут свое мнение в рамках обсуждения.
7. Я подготовил исходный текст программы, с подробными комментариями, который, надеюсь, в ближайшее время будет опубликован на Хабре. Думаю, что те, кто интересуется решением сложных задач из семейства NP-Complete, найдут для себя что-нибудь интересное.
8. Я хотел бы снова обратиться к членам ХабраСообщества, но уже по другому поводу. Здесь, в Марселе (Франция), идет процесс формирования команды France Fold Group, целью которой является исследование и разработка алгоритмов для предсказания физико-химических свойств высокомолекулярных соединений. Думаю, не стоит говорить, что это достаточно сложная задача, с многолетней историей, и, что над этой проблемой работают серьезные команды в разных странах, в том числе и команда Хасабиса из Deep Mind (можно посмотреть статью на Хабре (habr.com_Folding). Цель — создать сильную команду, которая не боится решать сложные задачи. Форма организации совместной работы — распределенная. Каждый член команды живет в своем городе и работает над проектом в свободное от основной работы время. Нужны программисты-исследователи (физики, химики, математики, биологи), и просто «безбашные»-программисты-(в квадрате). Напишите мне, если сочтете это интересным, выше приведен мой e-mail. Более подробно я смогу рассказать в ответном письме.
Предисловие к статье оказалось таким же длинным, как и сама статья. Семейный формат изложения на Хабре позволяет более свободно излагать свои мысли, но, судя по размеру, я достаточно свободно этим воспользовался. Хотелось написать кратко, а «получилась как всегда».
p.s. Я подумал, что членам Хабра-Сообщества будет интересно узнать, с какими трудностями я столкнулся при попытке опубликовать результаты исследования. Когда статья была подготовлена, я переформатировал ее в .tex формат согласно требованиям Journal of Artificial Intelligence Research (JAIR) и отправил туда. Там раньше были публикации на похожую тему. Особо можно выделить статью C. Gent, I.-P. Jefferson and P. Nightingale (2017) (Complexity of n-queens completion), в которой авторы доказали, что рассматриваемая проблема относится к множеству NP-Complete и рассказали о сложностях, с которыми столкнулись, в попытке решения этой задачи. В выводах авторы пишут: «For anybody who understands the rules of chess, n-Queens Completion may be one of the most natural NP-Complete problems of all» (Для всех кто понимает правила шахмат, задача n-Queens Completion может стать одним из самых естественных NP-Complete задач).
Через 10 дней мне пришел отказ из JAIR, с формулировкой: «статья не соответствует формату журнала», т.е. даже не взяли статью на рассмотрение. Такого ответа я не ожидал. Я полагал, что если журнал публикует статьи, в которых авторы делают вывод о большой сложности решения данной задачи и не приводят какого либо конкретного решения, то статья, в которой приводится эффективный алгоритм решения — будет, безусловно принята к рассмотрению. Однако, у редакции было свое мнение по этому поводу. (Полагаю, что там работают грамотные специалисты, и, скорее всего у них вызвало сомнение «наглое» названия статьи и все то, что там излагается. Подумали, «здесь, скорее всего какая-то ошибка и мягко послали меня подальше, ссылаясь на формат»).
Мне предстояло выбрать другое рецензируемое периодическое научное издание по соответствующей тематике. Вот тут я столкнулся с суровой действительностью. Дело в том, что примерно 80% всех журналов являются платными: либо я должен платить журналу приличную сумму, чтобы статья была свободно доступна всем читателям, либо нужно им отдать статью как подарок «в бантике», и они будут взимать плату с каждого, кто захочет ознакомиться с данным исследованием. И первый и второй варианты для меня принципиально неприемлемы. Этот способ рэкета издателей я хорошо почувствовал на себя, когда пытался ознакомиться с некоторыми публикациями.
Очередным журналом, где исповедуется принцип свободного доступа к информации был «SMAI Journal of Computational Mathematics». Здесь тоже отказали с той же формулировкой, правда намного быстрее — через два дня.
Дальше был выбран журнал: «Discrete Mathematics & Theoretical Computer Science». Здесь требования простые, вначале необходимо опубликовать статью в arXiv.org, и лишь после этого зарегистрировать статью для рассмотрения. Ладно, будем соблюдать правила — подал статью в arXiv.org. Написали мне, что опубликуют статью через 8 часов. Однако этого не произошло ни через 8 часов, не через 8 дней. Статья был на «удержании» у менторов, и только через 9 дней ее опубликовали. Никаких претензий по форме и сути статьи не было. Думаю, как и в случае с JAIR, у менторов были сомнения в возможности «такое сделать и об этом написать». Спустя некоторое время, после исправления технических ошибок, статья была обновлена и в окончательном виде вышла в ночь на новый год.
Я вынужден подробно остановиться на этом, чтобы показать, что на этапе публикации результатов исследования могут быть проблемы, которые не поддаются логическому объяснению.
Далее следует статья, перевод которой на английский, был опубликован в (arXiv.org).
1 Введение
Среди различных вариантов формулировки n-Queens problem, рассматриваемая задача the n-Queens Completion занимает особое положение ввиду своей сложности. В своей работе (Gent at all (2017)) показали, что the n-Queens Completion problem относится к множеству NP-Complete (showed that n-Queens Completion is both NP-Complete and # P-Complete). Предполагается, что решение данной проблемы, возможно, откроет нам путь к решению некоторых других задач из множества NP-Complete.
Задача формулируется следующим образом. Имеется композиция из k ферзей, которые непротиворечиво распределены на шахматной доске размера n x n. Требуется доказать, что данная композиция может быть комплектована до полного решения, и привести хотя бы одно решение, либо доказать, что такого решения не существует. Здесь, под непротиворечивостью, мы понимаем такую композицию из k ферзей, для которой выполняются три условия задачи: в каждой строке, каждом столбце, а также на левой и правой диагоналях, проходящих через ячейку, где расположен ферзь, не расположено более одного ферзя. Задача в таком виде была впервые сформулирована Nauk (1850).
1.1 Определения
Здесь и далее, размер стороны шахматной доски мы будем обозначать символом n. Решение мы будем называть полным, если все n ферзей непротиворечиво расставлены на шахматной доске. Все остальные варианты решения, когда количество k правильно расставленных ферзей меньше n — мы будем называть композицией. Назовем композицию из k ферзей положительной, если она может быть комплектована до полного решения. Соответственно, композицию, которую невозможно комплектовать до полного решения — назовем отрицательной. В качестве аналога «шахматной доски» размера n x n, мы будем рассматривать также «матрицу решения» размера n x n. В качестве примера, все алгоритмы, разработанные для решения поставленной задачи, будут представлены на языке Matlab.
Исследование проводилось на основе компьютерного моделирования (computational simulation). Чтобы проверить ту или иную гипотезу, мы проводили вычислительные эксперименты в широком диапазоне значений n= (10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 500, 800, 1000, 3000, 5000, 10000, 30000, 50000, 80000, 105, 3×105, 5×105, 106, 3×106, 5×106, 107, 3×107, 5×107, 8×107, 108) и, в зависимости от значения n, генерировали достаточно большие выборки для анализа. Назовем такой список »базовым списком значений n» для проведения вычислительных экспериментов. Все расчеты проводились на обычном компьютере. На момент сборки (начало 2013 года) это была достаточно удачная конфигурация: CPU — Intel Core i7–3820, 3.60 GH, RAM-32.0 GB, GPU- NVIDIA Ge Forse GTX 550 Ti, Disk device- ATA Intel SSD, SCSI, OS- 64-bit Operating system Windows 7 Professional. Назовем такой комплект просто — desktop-13.
2 Подготовка данных
Работа алгоритма начинается со считывания файла, который содержит одномерный массив данных о распределении произвольной композиции из k ферзей. Предполагается, что данные подготовлены следующим способом. Пусть имеется обнуленный массив Q (i)=0, i=(1, …, n), где индексы ячеек этого массива соответствуют индексам строк матрицы решения. Если в некоторой произвольной строке i матрицы решения располагается ферзь в позиции j, то выполняется присваивание Q (i)=j. Таким образом, размер композиции k, будет равен количеству ненулевых ячеек массива Q. (Например, Q=(0, 0, 5, 0, 4, 0, 0, 3, 0, 0) означает, что рассматривается композиция из k=3 ферзей на матрице n=10, где ферзи расположены в 3-ей, 5-ой и 8-ой строках, соответственно в позициях: 5, 4, 3).
3 Алгоритм проверки правильности решения n-Queens problem
Для исследований нам нужен алгоритм, который позволил бы за короткое время определить правильность решения n-Queens problem. Контроль расположения ферзей в каждой строке и каждом столбце выполняется просто. Вопрос состоит в учете диагональных ограничений. Мы могли бы построить эффективный алгоритм такого учета, если бы нам удалось сопоставить каждой ячейке матрицы решения определенную ячейку некого контрольного вектора, который однозначно характеризовал бы влияние диагональных ограничений на рассматриваемую ячейку. Тогда, на основе того, свободна или занята ячейка контрольного вектора, можно судить о том, свободна или закрыта соответствующая ячейка матрицы решения. Такая идея впервые была использована в работе Sosic & Gu (1990) для учета и накопления числа конфликтных ситуаций между различными позициями ферзей. Подобная идея используется нами в представленном ниже алгоритме, но только для учета того, свободна или занята ячейка матрицы решения. На рисунке 1, в качестве примера приведена шахматная доска 8×8 над которой сверху расположена последовательность из 24 ячеек.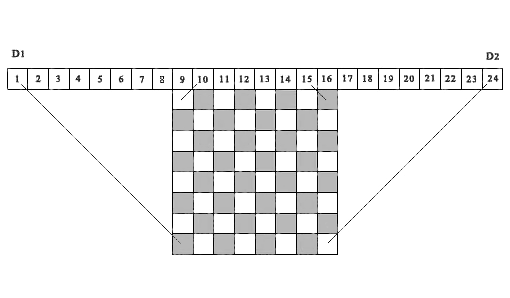
Рис. 1. Демонстрационный пример соответствия диагональных проекций ячеек матрицы, соответствующим ячейкам контрольных массивов D1 и D2, (n=8)
Рассмотрим первые 15 ячеек, как элементы контрольного вектора D1. Проекции всех левых диагоналей из любой ячейки матрицы решения попадают в одну из ячеек контрольного вектора D1. В самом деле, все такие проекции расположены внутри двух параллельных отрезков прямых, одна из которых соединяет ячейку матрицы (8,1) с первой ячейкой вектора D1, а вторая — ячейку матрицы (1,8) с 15-ой ячейкой контрольного вектора D1. Приведем аналогичное определение для правых диагональных проекций. Для этого, переместим вправо начало отсчета из ячейки 1 в ячейку 9, и рассмотрим последовательность из 16 ячеек, как элементы контрольного вектора D2 (на рисунке, это ячейки c 9-го по 24-ый).Проекции всех правых диагоналей из любой ячейки матрицы решения попадут в одну из ячеек этого контрольного вектора, начиная со 2-ой ячейки по 16-ую (на рисунке, с 10-ой по 24-ю). Здесь, все такие проекции, расположены между двумя отрезками параллельных прямых — отрезком, соединяющим ячейку (8,8) матрицы решения с ячейкой 16 вектора D2 (на рисунке ячейка 24), и отрезком, соединяющий ячейку (1,1) матрицы решения с ячейкой 2 контрольного вектора D2 (на рисунке ячейка 10). Проекции всех ячеек матрицы решения, лежащие на одной и той же левой диагонали, попадают в одну и ту же ячейку левого контрольного вектора D1, соответственно, проекции всех ячеек матрицы решения, лежащие на одной и той же правой диагонали, попадают в одну и ту же ячейку правого контрольного вектора D2. Таким образом, эти два контрольных вектора D1 и D2, позволяет вести полный контроль всех диагональных запретов для любой ячейки матрицы решения.
Важно отметить, что идею использования диагональных проекций на ячейки контрольных векторов для определения того, свободна или занята ячейка матрицы решения с координатами (i, j), позже была реализована также в работе Richards (1997). В ней приводится один из быстрых рекурсивных алгоритмов поиска всех решений, основанный на операциях с битовой маской. Важное отличие состоит в том, что указанный алгоритм предназначен для последовательного поиска всех решений, начиная с первой строки матрицы решения — вниз, или с последней строки матрицы — вверх. Предложенный нами алгоритм основан на том условии, что выбор номера каждой строки для расположения ферзя должен быть произвольным. Для рассматриваемого алгоритма это имеет принципиальное значение. Отметим, что представленный выше рисунок 1, построен нами по аналогии с тем, что опубликован в данной работе.
Программа для проверки того, является ли правильным данное решение n-Queens problem, или является ли верным данная композиция из k ферзей, выглядит следующим образом.
1. Для контроля диагональных запретов, создадим два массива D1(1: n2) и D2(1: n2), где n2= 2*n, и массив B (1: n) для контроля занятости столбцов матрицы решения. Обнулим эти три массива.
2. Введем в рассмотрение счетчик числа правильно установленных ферзей ( totPos = 0). Последовательно, в цикле, начиная с первой строки, рассмотрим все предоставленные позиции ферзей. Если Q (i) > 0, то на основе индекса строки i и индекса позиции ферзя в этой строке j = Q (i) сформируем соответствующие индексы для контрольных массивов D1(r) и D2(t):
r = n + j — i
t = j + i
3. Если будут выполнены все условия (D1(r) = 0, D2(t) = 0, B (j) = 0), то это будет означать, что ячейка (i, j) свободна и не попадает в проекционную зону диагональных ограничений, сформированных ранее установленными ферзями. Расположение ферзя в такой позиции является правильным. Если, хотя бы одно из этих условий не выполняется, то выбор такой позиции будет ошибочным, соответственно и решение будет ошибочным.
4. Если решение правильное, то инкрементируем счетчик числа правильно установленных ферзей (totPos=totPos+1), и закроем соответствующие ячейки контрольных массивов: (D1(r)=1, D2(t) = 1, B (j)=1). Таким образом, мы закроем все ячейки столбца (j) и те ячейки матрицы решения, которые расположены вдоль левой и правой диагоналей, пересекающихся в ячейке (i, j).
5. Повторим процедуру проверки для всех оставшихся позиций.
Возможно, это один из самых быстрых алгоритмов оценки правильности решения n-Queens problem. Время проверки одного миллиона позиций для матрицы решения 106×106 на desktop-13 составляет 0.175 секунды, что примерно соответствует времени нажатия клавиши «Enter». Очевидно, что данный алгоритм по времени счета является линейным относительно n.
4 Описание алгоритма решения задачи
Общее. n-Queens Completion problem является классической не детерминированной задачей. Основная сложность ее решения связана с вопросом выбора индекса строки и индекса позиции в этой строке, в условиях, когда пространство состояния имеет огромные размеры. Когда ведется поиск всех возможных решений, то такой проблемы не возникает. Мы должны рассмотреть все допустимые ветви поиска в пространстве состояния и то, в какой последовательности они рассматриваются, не имеет значения. Однако, когда произвольную композицию из k ферзей необходимо комплектовать до полного решения, то в этом случае нужен алгоритм выбора индексов строк и столбцов, который адекватно воспринимает существующую композицию и быстрее других приводит к получению решения. В данном проекте, вопрос с выбором мы решали исходя из следующего общего положения — если мы не можем сформулировать условия, которые дают предпочтение какой-либо строке, или какой-либо позиции в этой строке по сравнению с другими, то используется алгоритм случайного отбора на основе равномерно распределенных случайных чисел. Подобный метод случайного отбора для решения задач, в которых пространство состояния имеет огромные размеры, является вполне естественным. Один из выпусков серии Proceedings of a DIMACS Workshop (1999) был полностью посвящен использованию метода случайного отбора при разработке алгоритмов решения сложных задач. Правильная реализация алгоритма случайного отбора может быть достаточно продуктивным решением, хотя, это является необходимым, но не достаточным условием завершения решения. Публикация Sosic and Gu (1990) является одним из первых исследований, где использовался алгоритм случайного отбора для решения n-Queens Problem. В основе рассмотренного ими алгоритма лежит достаточно простая и лаконичная идея. Пусть имеется последовательность чисел от 1 до n, которые случайно переставлены местами. Такой набор чисел имеет важное свойство. Состоит оно в том, что каким бы образом не были распределены эти числа на различных строках матрицы решения в качестве позиций ферзя (по одному числу на строку), всегда будут выполнены первые два правила в постановке задачи: в каждой строке и каждом столбце будет расположено не более одного ферзя. Однако, только часть, полученных таким образом позиций будут свободны от диагональных ограничений. Другая часть будет находиться в состоянии «конфликта» с ранее установленными ферзями. Для выхода из этой ситуации, авторы использовали метод сравнения и перестановки местами конфликтующих позиций для получения полного решения. В предложенном нами алгоритме невозможны конфликтные ситуации, так как на каждом шаге решения задачи, ферзь устанавливается в ячейку рассматриваемой строки только в том случае, если ячейка свободна.
4.1 Выбор модели для организации процедуры Back Tracking (BT)
В процессе поиска решения задачи, может наступить ситуация, когда последовательная цепочка решения приводит в тупик. Это «генетическое» свойство не детерминированных задач. В таком случае, нужно сделать возврат назад, на один из предыдущих шагов, восстановить состояние задачи в соответствии с этим уровнем и начинать снова поиск решения с этой позиции. Вопрос состоит в том, на какой из предыдущих уровней следует возвращаться и сколько таких уровней должно быть (под уровнем, мы понимаем некоторый шаг решения задачи с заданным количеством правильно установленных ферзей). Очевидно, что выбор уровня решения для возврата назад, является такой же актуальной задачей, как и выбор индекса строки или индекса позиции в этой строке. Поэтому, независимо от подхода к решению данной задачи, необходимо предварительно определить количество базовых уровней для возврата назад, а также механизм и условия возврата на один из этих уровней. В предложенном нами алгоритме, мы делим матрицу решения на три базовых уровня. Это точки возврата. Если, в результате решения, возникает тупиковая ситуация, то, в зависимости от параметров задачи, мы возвращаемся назад на один из этих трех базовых уровней. Первый базовый уровень (baseLevel1) соответствует состоянию, когда проверка данных рассматриваемой композиции завершена. Это начало работы программы. Значения следующих двух базовых уровней (baseLevel2 и baseLevel3) зависят от размера матрицы n. Эмпирическая зависимость этих базовых значений от размера матрицы решения была установлена на основе большого числа вычислительных экспериментов. Для более точного представления этой зависимости, мы разделили весь рассматриваемый интервал от 7 до 108 на две части. Пусть u=log (n), тогда, если n < 30 000, то
baseLevel2 = n — round (12.749568*u3 — 46.535838*u2 + 120.011829*u — 89.600272)
baseLevel3 = n — round (9.717958*u3 — 46.144187*u2 +101.296409*u — 50.669273)
иначе
baseLevel2 = n — round (-0.886344*u3 + 56.136743*u2 + 146.486415*u + 227.967782)
baseLevel3 = n — round (14.959815*u3 — 253.661725*u2 +1584.713376*u — 3060.691342)
4.2 Блочная структура
Алгоритм построен в виде последовательности из пяти блоков-событий, где каждое событие связано с выполнением определенной части решения задачи. Алгоритмы обработки в каждом блоке различаются друг от друга. Только три блока из этих пяти служат для формирования последовательной цепочки решения, а оставшиеся два блока являются подготовительными. Выбор номера блока, с которого начинаются расчеты, зависит от значения n и от результатов сравнения размера композиции k со значениями baseLeve2 и baseLevel3. Исключением является интервал значений n=(7, …,99), который можно назвать «турбулентной зоной» ввиду особенностей поведения алгоритма на этом участке. Для значений n=(7, …,49), независимо от размера композиции, после ввода и контроля данных, расчеты начинаются с 4-го блока. Для значений n=(50, …,99), в зависимости от размера композиции, расчеты начинаются либо со второго блока, либо с четвертого. Как было сказано выше, на каждом шаге решения задачи рассматриваются только те позиции в строке, которые не попадают в зону ограничений, созданных ранее установленными ферзями. Именно такие позиции называются свободными.
Опишем кратко, какие расчеты выполняются в каждом из этих пяти блоков программы.
4.3 Начало алгоритма
Производится ввод данных и проверка правильности композиции. На каждом шаге проверки производится изменение ячеек контрольных массивов. Проводится учет количества правильно установленных ферзей. Если в композиции нет ошибок, то решение продолжается, иначе выводится сообщение об ошибке. После завершения проверки, создаются копии основных массивов для их повторного использования на данном уровне. После этого управление передается в Блок-1.
4.4 Блок-1
Начало формирования ветви поиска. Рассматривается k ферзей, расположенных на шахматной доске в качестве стартовой позиции. Требуется продолжить комплектацию этой композиции и расположить ферзи на шахматной доске до тех пор, пока их общее количество не окажется равным baseLevel2. Алгоритм, который используется здесь, называется randSet & randSet. Связано это с тем, что здесь постоянно сравниваются два случайных списка индексов, в поисках пар, свободных от соответствующих диагональных ограничений. Для этого выполняются следующие действия:
a) формируются два списка: список индексов свободных строк и список индексов свободных столбцов;
b) производится случайная перестановка чисел в каждом из этих списков;
c) в цикле, каждая последовательная пара значений (i, j), где индекс (i) выбирается из списка индексов свободных строк, а индекс (j) — из списка индексов свободных столбцов, рассматривается как потенциальная позиция ферзя и проверяется, попадает ли данная позиция в проекционную зону диагональных исключений.
Если правило диагональных исключений не нарушается, то позиция считается верной, и в данную позицию располагается ферзь. После этого, производится инкрементация счетчика числа правильно установленных ферзей, и изменяются соответствующие ячейки контрольных массивов. Если позиция (i, j) попадает в зону диагональных ограничений, сформированных ранее установленными ферзями, то ничего не меняется и совершается переход к рассмотрению следующей пары значений.
Когда завершается цикл сравнения всех пар списка, то, на основе оставшихся индексов, которые оказались в зоне диагональных исключений, снова формируется список индексов оставшихся свободных строк и свободных столбцов, и данная процедура повторно выполняется до тех пор, пока общее число правильно расставленных ферзей (totPos) не окажется равным или превысит граничное значение baseLevel2. Как только выполняется это условие, управление передается в Блок-2. Если окажется, что в результате поиска решения, возникла такая ситуация, что из всего списка индексов оставшихся свободных строк и свободных столбцов, ни одна из пар не подходит для расположения ферзя, то в этом случае, восстанавливаются исходные значения контрольных массивов на основе ранее сформированных копий, и управление передается на начало Блока-1 для повторного счета.
4.5 Блок-2
Данный блок служит в качестве подготовительного этапа для перехода в Блок-3. На данном уровне количество оставшихся свободных строк (freeRows) значительно меньше n. Это позволяет перенести события из исходной матрицы размера n x n на матрицу меньшего размера L (1: freeRows, 1: freeRows). При этом, на основе информации об оставшихся свободных строках и свободных столбцах в исходной матрице решения, записываются нули в соответствующие ячейки массива L, показывающие, что данные ячейки свободны. При таком «проекционном» переходе сохраняется соответствие индексов строк и столбцов новой матрицы, с соответствующими индексами исходной матрицы. Важно отметить, что хотя, в процессе решения данной задачи, все события разворачиваются на исходной матрице размера n x n, и такая матрица является главной ареной действий, реально такая матрица не создается, а рассматриваются только контрольные массивы учета индексов строк A (1: n) и столбцов B (1: n) этой матрицы.
Наряду с массивом L, в данном блоке формируются также два рабочих массива rAr (1: freeRows) и tAr (1: freeRows), для сохранения соответствующих индексов контрольных массивов D1 и D2. Это связано с тем, что когда мы устанавливаем очередной ферзь в ячейку (i, j) исходной матрицы размера n x n, то после этого должны исключить ячейки массива L, попадающие в проекционную зону диагональных исключений исходного «большого» массива. Так как контроль диагональных ограничений производится только в пределах исходной матрицы размера n x n, то наличие рабочих массивов rAr и tAr позволяет сохранить соответствие и транслировать запрещенные ячейки в пределы массива L. Это значительно упрощает учет исключенных позиций.
После завершения подготовительной работы в данном блоке, создаются копии основных массивов для повторного использования на данном уровне, и управление передается в Блок-3.
4.6 Блок-3
В данном блоке продолжается формирование ветви поиска решения на основе данных, подготовленных в предыдущем блоке. Количество строк, в которых правильно установлены ферзи, равно или превышает значение baseLevel-2. Требуется продолжить комплектацию, пока количество установленных ферзей не окажется равным baseLevel-3. Здесь используется алгоритм поиска решения rand & rand, т.е. для формирования позиции ферзя, вместо списка свободных индексов, используются только два индекса, случайное значение индекса свободной строки и случай
