Моделирование динамических систем (метод Лагранжа и Bond graph approach)16.08.2016 15:18

Всем доброго дня. В данной статье хочу показать один из графических методов построения математических моделей для динамических систем, который называется Bond graph («bond» — связи, «graph» — граф). В русской литературе, описания данного метода, я нашел только в Учебном пособии Томского политехнического университета, А.В. Воронин «МОДЕЛИРОВАНИЕ МЕХАТРОННЫХ СИСТЕМ» 2008 г. Также показать классический метод через уравнение Лагранжа 2 рода.

880d035deee24b078b70bc8a863f8625.png

Метод Лагранжа


Я не буду расписывать теорию, покажу этапы расчётов и с небольшими комментариями. Лично мне легче учиться на примерах, чем 10 раз читать теорию. Как мне показалось, в русской литературе, объяснение данного метода, да и вообще математики или физики, очень насыщено сложными формулами, что соответственно требует серьезного математического бэкграунда. Во время изучения метода Лагранжа (учусь в Туринском политехническом университет, Италия), я изучал русскую литературу, чтобы сопоставить методики расчётов, и мне было тяжело следить за ходом решения данного метода. Даже вспоминая курсы по моделированию в «Харьковском авиационном институте», вывод подобных методов был очень громоздким, и никто не затруднял себя в попытке разобраться в этом вопросе. Вот этому я решил написать, методичку для построения мат моделей по Лагранжу, как так оказалось это совсем не сложно, достаточно знать как считать производные по времени и частные производные. Для моделей по сложнее еще добавляются матрицы поворота, но в них тоже нет ничего сложного.

Особенности методов моделирования:

  • Ньютона-Эйлера: векторные уравнения, основанные на динамическом равновесии сил (force) и моментов (moments)
  • Лагранжа: скалярные уравнения, основанные на функция состояния связанных с кинетической и потенциальной энергией (energies)
  • Бонд-граф: метод основанный на течении мощности (power) между элементами системы

Начнем с простого примера. Масса с пружиной и демпфером. Пренебрегаем силой тяжести.

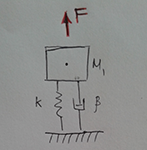
a23fe4677c5d45c9868afdca24f11cf2.png

Рис 1. Масса с пружиной и демпфером

Первым делом обозначаем:

  • начальную системы координат (НСК) или неподвижную ск R0(i0, j0, k0). Где? Можно тыкнуть пальцем в небо, но подёргав кончиками нейронов в мозгу, проходит идея поставить НСК на линии движения тела М1.
  • системы координат для каждого тела с массой (у нас М1 R1(i1, j1, k1)), ориентация может быть произвольной, но зачем усложнять себе жизнь, ставим с минимальным отличием от НСК
  • обобщеные координаты q_i (минимальное количество переменные которыми можно описать движение), в данном примере одна обобщенная координата, движение только вдоль оси j

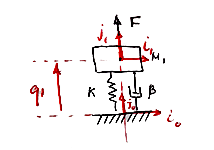
3809e73ad606484d89cbc55265e95142.png

Рис 2. Проставляем системы координат и обобщенные координаты

Далее найдем положение и скорости всех тел. В данном примере одно тело М1:

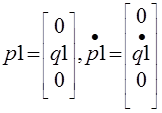
174475f2d10040a993b6081601c522f6.png

Рис 3. Позиция и скорость тела М1

После найдем кинетическую © и потенциальную (Р) энергии и диссипативную функцию (D) для демпфера по формулам:

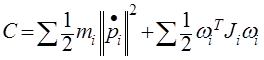
42f135444c4d44ef858e6087f42d2e92.png

Рис 4. Полная формула кинетической энергии

В нашем примере вращения нет, вторая составляющая равна 0.

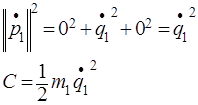
65fb7ebdf83a440db0d3f26743b4679d.png

41b588e8a3b8406083d5c56aa0b01771.png

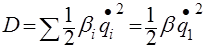
1cb1d5c16a914298bd9b6a1621bcaf1f.png

Рис 5. Расчет кинетической, потенциальной энергии и диссипативной функции

Уравнение Лагранжа имеет следующий вид:

01857d41b8ad498f97099ce33f72f048.png

Рис 6. Уравнение Лагранжа и Лагранжиан

Дельта W_i это виртуальная работа совершенная приложенными силами и моментами. Найдем ее:

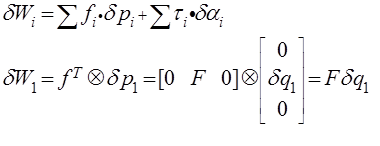
659d021c4af74996b70da2a863eaa2ba.png

Рис 7. Расчет виртуальной работы

где дельта q_1 виртуальное перемещение.

Подставляем всё в уравнение Лагранжа:

da607094310a4e41bbd127457a8cdf1b.png

Рис 8. Полученная модель массы с пружинной и демпфером

На этом метод Лагранжа закончился. Как видно не так сложно, но это все же очень простой пример, для которого скорее всего метод Ньютона-Эйлера даже был бы проще. Для более сложных систем, где будет несколько тела, повернутые друг относительно друга на разные угол, метод Лагранжа будет легче.

Метод Bond graph
Сразу покажу так выглядит модель в bond-graph для примера с массой пружиной и демпфером:
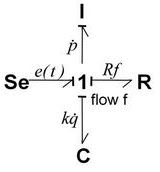
3ce336e3198044b8861b549f0f8c32a1.png

Рис 9. Bond-graph массы с пружинной и демпфером

Здесь придётся рассказать немного теории, которой хватит для построения простых моделей. Если кто нибудь заинтересован можете почитать книгу ([Wolfgang Borutzky] Bond Graph Methodology) или (Воронин А.В. Моделирование мехатронных систем: учебное пособие. — Томск: Изд-во Томского политехнического университета, 2008).

Определим для начала, что сложные системы состоят из нескольких доменов. Например электродвигатель состоит из электрической и механической частей или доменов.

Bond graph основан на обмене мощности между этими доменами, подсистемами. Заметим, что обмен мощностью, любой формы, всегда определяется двумя переменными (переменные мощности) с помощью которых, мы можем изучать взаимодействие различных подсистем в составе динамической системы (см. таблицу).

1a67ab0b89ff4c3fa63ba7841f87eb29.png

Как видно из таблицы выражение мощности везде практически одинаковое. В обобщении, Мощность — это произведение »потока — f» на »усилия — e».

Усилие (англ. effort) в электрическом домене это напряжение (e), в механическом — сила (F) или момент (T), в гидравлике — давление (p).

Поток (англ. flow) в электрическом домене это ток (i), в механическом — скорость (v) или угловая скорость (omega), в гидравлике — поток или расход жидкости (Q).

Принимая данные обозначения, получаем выражение для мощности:

b603f7236b46455b88f7594ec2a4aac7.png

Рис 10. Формула мощности через мощностные переменные

В языке bond-graph соединение между двумя подсистемами которые обмениваются мощностью представлена связью (англ. bond). По этому и называется данный метод bond-graph или граф-связей, связной граф. Рассмотрим блок-диаграмму связей в модели с электродвигателем (это еще не bond-graph):

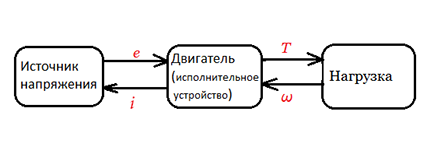
4b3b2cd8b15040048d8195fb6701a1eb.png

Рис 11. Блок-диарамма потока мощности между доменами

Если у нас источник напряжения, то соответственно он генерирует напряжение и отдает его двигателю на отмотки (по этому стрелка направлена в сторону двигателя), в зависимости от сопротивления обмотки появляется ток по закону Ома (направлен от двигателя к источнику). Соответственно одна переменная является входом в подсистему, а вторая необходима должна быть выходом из подсистемы. Здесь напряжение (effort) — вход, ток (flow) — выход.

Если использовать источник тока, как поменяется диаграмма? Правильно. Ток будет направлен к двигателю, а напряжение к источнику. Тогда ток (flow) — вход, напряжение (effort) — выход.

Рассмотрим пример в механике. Сила, действующая на массу.

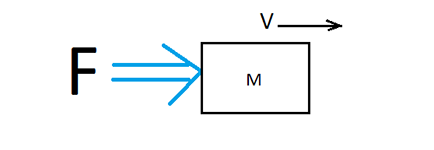
889ab5b3d1634b57ab83c9e93228a202.png

Рис 12. Сила приложенная к массе

Блок-Диаграмма будет следующей:

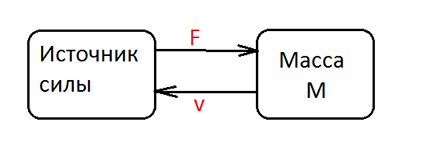
448e9c72cb92487384cbab582ea9210d.png

Рис 13. Блок-диаграмма

В этом примере, Сила (effort) — входная переменная для массы. (Сила приложена к массе)
По второму закону Ньютона:

47c96b0c066d4cc8865c2d57614ff3e4.png

Масса отвечает скоростью:
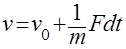
f86f9022c25a4cfa9406ea7ce06b2df2.png

В этом примере если одна переменная (сила  — effort) является входом в механический домен, то другая мощностная переменная (скорость  — flow) — автоматически становится выходом.

Что бы различать, где вход, а где выход, используется вертикальная линия на конце стрелки (связи) между элементами, эту линию называют знак причинности или причинная связь (causality). Получается: приложенная сила — причина, а скорость — следствие. Этот знак очень важен для правильного построения модели системы, так как причинность — это следствие физического поведения и обмена мощностями двух подсистем, по этому выбор расположения знака причинности не может быть произвольным.

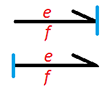
5eb9f31d47e54f5b8d55414e3df845a4.png

Рис 14. Обозначение причинной связи

Эта вертикальная линия показывает какая подсистема получает усилие (effort) и как следствие производить поток (flow). В примере с массой будет так:

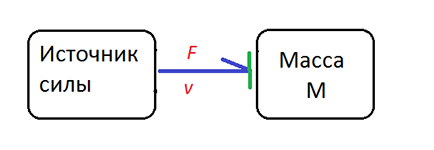
091bbf8d608a48c3a6c4a806e08bf201.png

Рис 14. Причинна связь для силы действующей на массу

По стрелке понятно что на вход для массы — сила, а выход — скорость. Это делается, что бы не загромождать стрелками схему и систематизации построения модели.

Следующий важный момент. Обобщённый импульс (количество движения) и перемещение (энергетические переменные).

Таблица мощностных и энергетический переменных в разных доменах
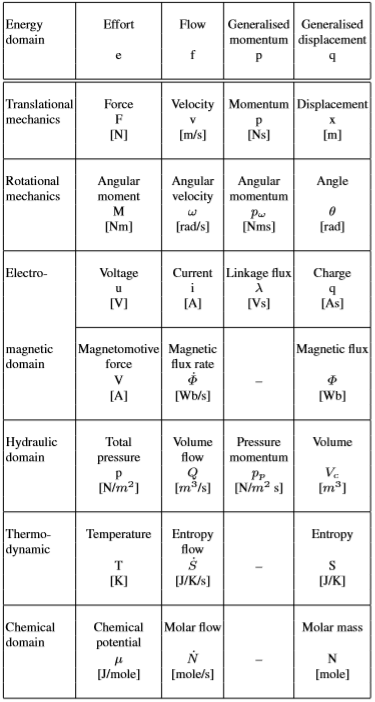
d64996201e904057822f2a035a33d622.png

Таблица выше вводит две дополнительные физические величины, используемые в методе bond-graph. Они называются обобщенный импульс (р) и обобщенное перемещение (q) или энергетические переменные, и получить их можно интегрированием мощностных переменных по времени:
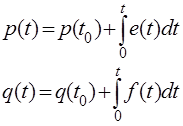
180fc7c64e1f46faab473900e5a991c3.png

Рис 15. Связь между мощностными и энергетическими переменными

В электрическом домене:

Исходя из закона Фарадея, напряжение на концах проводника равняется производной от магнитного потока через этот проводник.

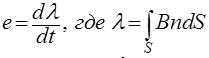
274a178c74c34ee1b890b86e06781291.png

А Сила тока — физическая величина, равная отношению количества заряда Q, прошедшего за некоторое время t через поперечное сечение проводника, к величине этого промежутка времени.
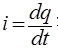
4a38ce18ad2d430cbbb2866d7f31229d.png

Механический домен:

Из 2 закона Ньютона, Сила — производная по времени от импульса

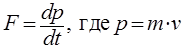
2075f5a01c034965b46a9cf53fc75261.png

И соответственно, скорость  — производная по времени от перемещения:
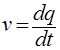
75f6658d97854ba0ab7996340d58644f.png

Обобщим:
b6c69c33f41d4a70a65ba8bb7c16dd4a.png

Базовые элементы


Все элементы в динамических системах, можно разделить на двухполюсные и четырехполюсные компоненты.
Рассмотрим двухполюсные компоненты:

Источники
Источники бывают как усилия, так и потока. Аналогия в электрическом домене: источник усилия — источник напряжения, источник потока — источник тока. Причинные знаки для источников должны быть только такие.

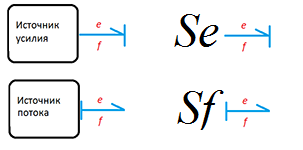
5a4a123a931d417e95aab02731fb6568.png

Рис 16. Причинные связи и обозначение источников

Компонент R — диссипативный элемент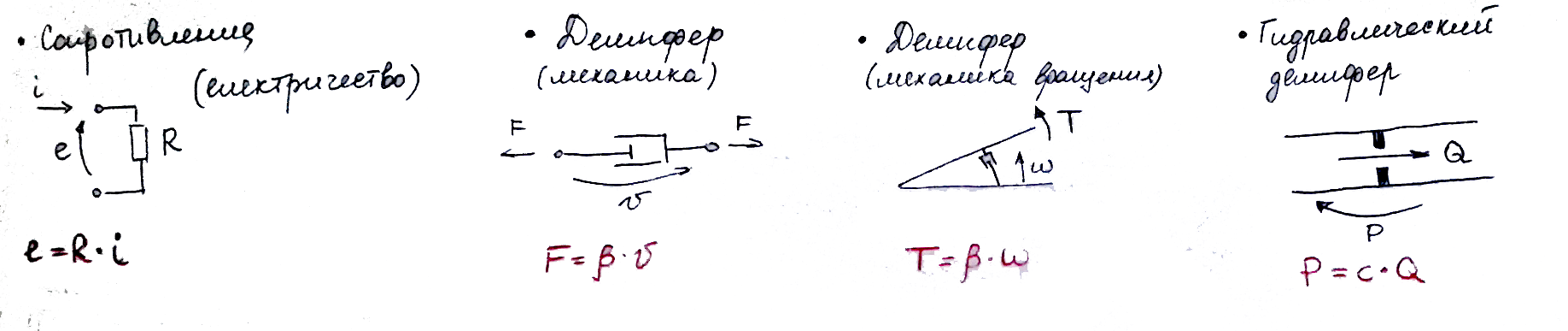
8a8715bc40814f35b7235d4863f0fbdc.png

Компонент I — инерциальный элемент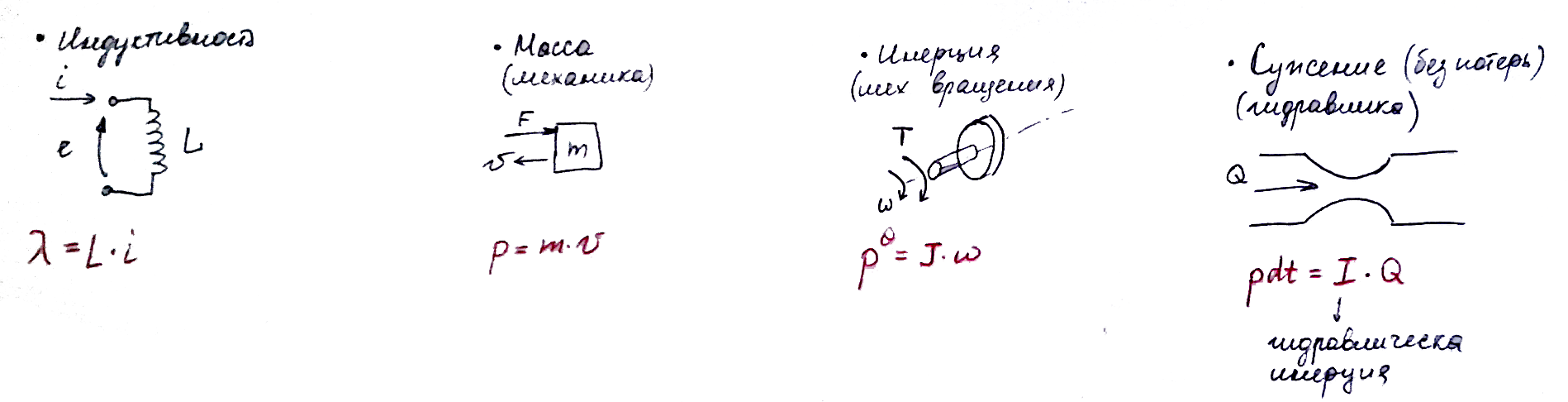
ff3d7206704b40049089cc2c6d77cc5c.png

Компонент C — емкостной элемент
b116af03ebe145e7ac9bc41b09876d3d.png

Как видно из рисунков, разные элементы одного типа R, C, I описываться одинаковыми уравнениями. ТОЛЬКО есть отличие для электрической емкости, это нужно просто запомнить!

Четырёхполюснике компоненты:

Рассмотрим два компонента трансформатор и гиратор.

  1. Идеальный Трансформатор (TF) связывает величины одного типа между входом и выходом
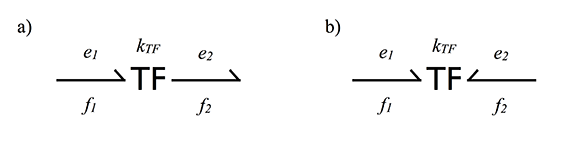
    83d2c9273c6d425ea5b92aa63c3f3847.png

    Формулы описывающая трансформатор из рисунка, а и b соответственно: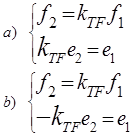
    c559683cc5ff45ffa14d37e0eaf0904d.png

    Причинные знаки ставиться только как показано ниже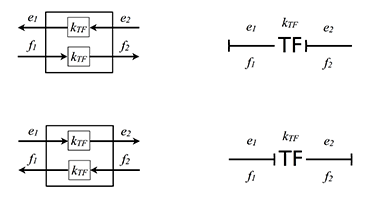
    8aee5e8ff0c240e5b5c150954bb765f3.png

    Вот так нельзя: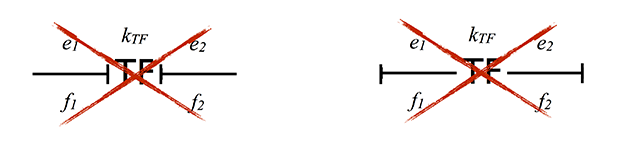
    28c735d2310b4cf5a5f692dad793e86a.png
    Примеры трансформатора в механическом домене может быть зубчатая передача, Рычаг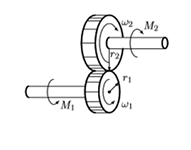
    25d78f7822fd4028abf76c69f45528d2.png13d60469682749fbb5e5910817675ad6.png

    Обычный трансформатор — в электричестве. Гидравлический поршень — в гидравлике.
  2. Гиратор (GY). Идеальный Гиратор связывает поток с одной стороны с усилием с другой.
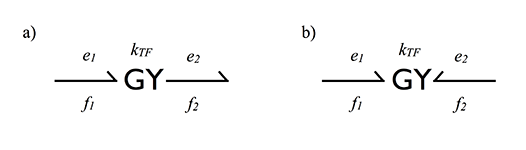
    dc8c46d33810411ea86e4338146c627f.png

    Формулы:
    dc13ff9242864e078ef6d58e54fd75d1.png

    Допустимая причинность для гиратора: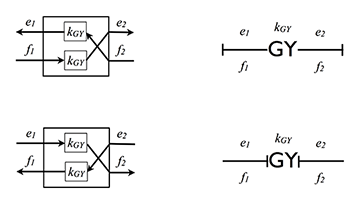
    1734b5e4d43b4593baa4c475b91487ff.png

    Ошибочная причинность:
    1801470a76e04f80bba2ddf2b8fc9976.png

    Примеры гираторов: в механике это двигатель постоянного тока, в электронике — соленоид (линейный актуатор).

Последними важными компонентами в методе bond-graph выступают соединения. Существует два типа узлов:

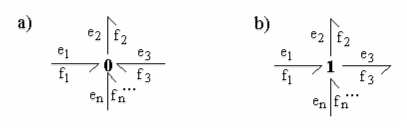
d14777a8b7cb4fd8b33d0e55e0d03f87.png

  • Узел типа 0 (а) — они имеют общее усилие и только одна причинная связь должна входить в 0-узлу, остальные должны выходить.
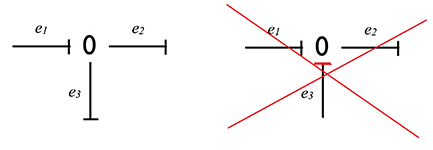
    c6c04793e8ec464cbed826f8eb04eea6.png

    Рассмотрим пример расчетов 0-узла: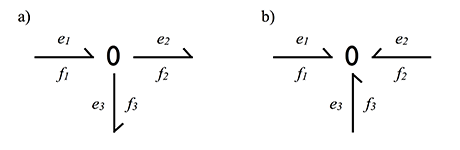
    29c64b12936545c0a28076358e09fd95.png

    а) 0 значит все усилия равны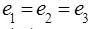
    66bf20bf0bb24732b48efc7064c9d25a.png

    Так как узел не аккумулирует и не рассеивает энергию, тогда алгебраическая сумма входящий мощностей должна равняться нулю.
    02ca9e4f64be45c49ee415efc17539a3.png

    Учитываю предыдущее уравнение получим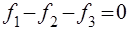
    7ce5d56cb5c14585aa3f7ba358288454.png

    b) Для второго варианты получим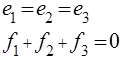
    f218fff1c9d84253ba1beacb69a00aa5.png

  • Узел типа 1 (b) — они имеют общий поток и только одна причинная связь должна выходить, остальные должны входить в 1-узел.
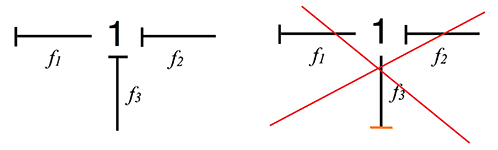
    691aaa16395846138ad49c5d4ac71219.png

    Рассмотри расчет 1-узла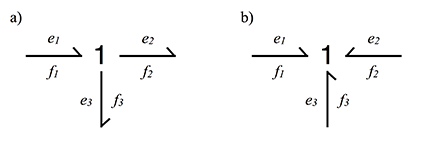
    32b210d552a4462b8b8dc82eaad88891.png

    а) 1 узел имеет общий поток, значит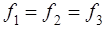
    24b6836070954e3a94eac284f767f97a.png

    Так как узел не аккумулирует и не рассеивает энергию, тогда алгебраическая сумма входящий мощностей должна равняться нулю.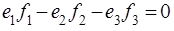
    c7cc0ab23dd2457e9e00ca9280e345cf.png

    Учитывая предыдущее уравнение получим: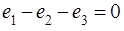
    02f75afe1477479ea9fa6942c03b9fb6.png

    b) Здесь будет: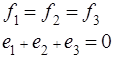
    1e6ec038e73341c983eab2263dfc029b.png


На этом с компонентами закончили.

Основные этапы для проставления причинных связей после построения bond-graph:

  1. Проставить причинные связи всем источникам
  2. Пройтись по всем узлам и проставить причинные связи после пункта 1
  3. Для компонентов I присвоить входную причинную связь (усилие входит в этот компонент), для компонентов С присваиваем выходную причинную связь (усилие выходит из этого компонента)
  4. Повторить пункт 2
  5. Проставить причинные связи для компонентов R

На этом мини-курс по теории закончим. Теперь у нас есть все необходимое для построения моделей.
Давайте решим пару примеров. Начнем с электрической цепь, лучше понять аналогию построения bond-graph.
Пример 1
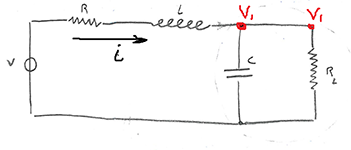
744d4cbc79514be0bc12ce9eb03a7240.png

Начнем построение bond-graph с источника напряжения. Просто пишем Se и ставим стрелку.
80c67c2ace424ea0b05fb29c85b64fec.png

Видите все просто! Смотрим далее, R и L соединены последовательно, значить в них течет одинаковый ток, если говорить в мощностных переменных — одинаковый поток. Какой узел имеет одинаковый поток? Правильный ответ 1-узел. Присоединяем к 1-узлу источник, сопротивление (компонент — R) и индуктивность (компонент — I).
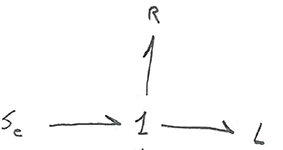
abff4a0390b0414db24124ec65c10302.png

Далее у нас емкость и сопротивление в параллели, значить они имеют одинаковое напряжение или усилие. 0-узел подойдет как никто другой. Соединяем емкость (компонент С) и сопротивление (компонент R) к 0-узлу.
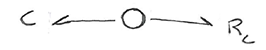
288a2070431243f8a1c18f1d904b4b44.png

Узлы 1 и 0 тоже соединяем между собой. Направление стрелок выбирается произвольное, направление связи влияет только на знак в уравнениях.

Получиться следующий граф связей:

32f28d3dcaf4419cb6abaa207c44c1dd.png

Теперь нужно проставить причинные связи. Следуя указаниям по последовательности их проставления, начнем с источника.

  1. Мы имеем источник напряжения (усилия), такой источник имеет только один вариант причинности — выходную. Ставим.
  2. Далее есть компонент I, смотрим что рекомендуют. Ставим
  3. Проставляем для 1-узла. Есть
  4. 0-узел должен иметь один вход и все выходные причинные связи. У нас есть пока одна выходная. Ищем компоненты С или I. Нашли. Ставим
  5. Проставляем что осталось

fbd01fe0bbd849428a50bd806459664c.png
Вот и все. Bond-graph построен. Ура, Товарищи!

Осталось дело за малым, написать уравнения, описывающие нашу систему. Для этого составим таблицу с 3 столбцами. В первом будут все компоненты системы, во втором входная переменная для каждого элемента, а в третьем — выходная переменная, для токого же компонента. Вход и выход мы уже определили причинностнными связями. Так что проблем возникнуть не должно.

Прономеруем каждую связь для удобства записи уровнений. Уравнения для каждого элемента берем из перечня компонентов C, R, I.

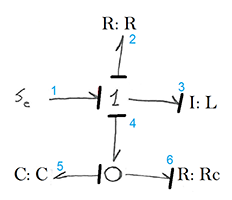
106dd57f04bd4b7dbcf60e4f7fc5a6a5.png

80c7488c0d00499da4ffd65402b2019c.png

Составив таблицу определим переменные состояния, их в данном примере 2, p3 и q5. Далее нужно записать уравнения состояния:
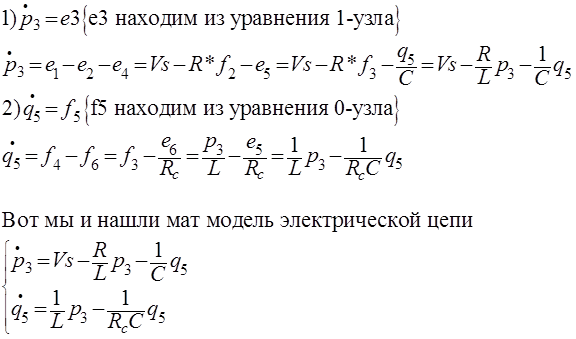
799c966a91214455a92e34ee47b4bf58.png

Вот и все модель готова.

Пример 2. Сразу хочу извениться за качество фото, главное что можно прочитать
Решим еще один пример для механической системы, тот же что мы решали методом Лагранжа. Я показу решение без комментариев. Проверим какой из данных методов проще, легче.

6f8a6e7134e64eceb6fc20a88d641c73.png

В матбале были составлены обе мат модели с одинаковыми параметрами, полученые методом Лагранжа и bond-graph. Результат ниже:

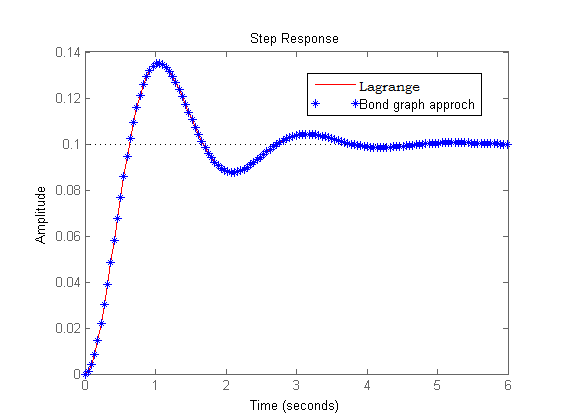
52058fd8a35f427bbdd139f21295b492.png


Итог: для меня bond-graph показался интереснее. По моим наблюдениям, его лучше использовать для комплексных систем (мульти-доменных систем, мехатронных систем). Например, мощный симулятор мульти-доменных систем AMESim, использует этот метод для построения мат моделей. В робототехнике, скорее всего, легче будет метод Лагранжа. Кто пользуется данными методами, буду рад услышать ваши выводы, комментарии.

Комментарии (1)

  • 16 августа 2016 в 13:50

    0

    ↑

    ↓

    Потрудитесь ошибки (грамматические, орфографические) исправить, пожалуйста.

© Habrahabr.ru