Мечта детства или поиск альтернативы машине Тьюрингита
В году где-то 1993 (учился я тогда во 2-ом классе) после просмотра на видеомагнитофоне с «подпольным» переводом фильма «Терминатор 2: Судный день», у меня появилась детская мечта сделать такого робота, который смог бы не только воевать, но и делать домашние задания по русскому языку за меня моим почерком, чтобы учительница не заметила (дико не любил я тогда этот предмет).
Прошло время, но даже сейчас, без преувеличения можно сказать, что возможности искусственного интеллекта, заложенные в, так называемом, нейропроцессоре робота-терминатора, роль которого исполнял Арнольд Шварценеггер, до сих пор остаются фантастическими. Ведь очевидно, что для того, чтобы какая-либо задача была решена при помощи средств вычислительной техники, она, прежде всего, должна быть формализована. А так как по состоянию на сегодняшний день в Мире не существует единого и полного формального описания искусственного интеллекта, этот вопрос остаётся не решённым. И пока что, само выражение «искусственный интеллект» носит больше некий субъективный характер, применимый лишь к отдельным задачам (ну, это лично моё мнение, может быть я и не прав). Но, даже если всё-таки и удастся процессы, происходящие в головном мозге человека, описать при помощи математических формул, то есть, как раз найти тот самый способ формализации искусственного интеллекта, то вряд ли возможности современной вычислительной техники позволят его реализовать. Дело тут в том, что все формализованные алгоритмы, по состоянию на сегодняшний день, могут быть реализованы двумя способами:
- программной реализацией (на микропроцессорной технике);
- аппаратной реализацией (как правило, на программируемой логике).
Сами по себе микропроцессоры и микросхемы с программируемой логикой (ПЛИС) — два, принципиально разных способа реализации алгоритмов. Есть ещё и третий вариант — использование систем на кристалле, но это не более чем размещение на одной подложке ядер микропроцессоров (как аппаратных ядер, так и soft-ядер) и программируемой логики, с последующим распределением задач между ними, то есть смесь первых двух вариантов.
В наше время, конечно, уже появились и те самые (хотя нет, не те самые) нейронные процессоры (про один из них написано здесь), хотя, по сути искусственный нейрон — не более чем математическая модель, или как раз та самая попытка формализовать работу биологического нейрона, которая, опять же, реализуется либо программно с применением процессоров, либо аппаратно с применение программируемой логики, ну или с применением ASIC (грубо говоря, то же самое, что и ПЛИС, только в ПЛИС связи между логическими вентилями задаются программно, а в ASIC — аппаратно), как видите ничего принципиально нового.
Микропроцессоры и ПЛИС — две абсолютно разные темы, и далее здесь пойдёт речь о микропроцессорах.
Я думаю, ни для кого не секрет, что практически все современные процессоры представляют собой, тот или иной способ реализации (это, конечно весьма условно, но тем не менее) машины Тьюринга. Их особенность в том, что очередная, для выполнения, команда выбирается из памяти последовательно, её адрес, при этом, генерируется подряд счётчиком команд, либо содержится в определённых полях предыдущей команды. И очевидно, что процессорам работающим по таким принципам до возможностей того самого терминатора ещё дальше чем медному котелку до Китая пешком. И тут же возникает вопрос: «А существует ли альтернатива такому способу реализации программных алгоритмов, которые смогли вывести бы машинные вычисления на принципиально новый уровень, не выходя за рамки возможностей современной электроники?». В ВУЗах, на специальностях, тем или иным образом, связанных с вычислительной техникой, читают курс лекций, в котором рассказывается об организации ЭВМ и систем, и, среди прочего, в этом курсе рассказывается, что все, существующие на сегодняшний день, механизмы программной реализации алгоритмов исполняются так:
- очередная команда или набор независимых команд последовательности, считывается из памяти и выполняется тогда, когда выполнена предыдущая команда (набор независимых команд), как было сказано выше, так работает большинство современных процессоров, реализуя принципы машины Тьюринга;
- команда считывается из памяти и выполняется тогда, когда доступны все её операнды (потоковые вычисления);
- команды объединяются в процедуры, внутренне, каждая из которых выполняется как в первом случае (то есть, внутри каждой из таких процедур команды исполняются последовательно по принципам машины Тьюринга), при этом, внешне, сами процедуры исполняются как во втором случае, то есть по мере готовности и доступности всех необходимых операндов (макропотоковые вычисления, представляющие смесь первых двух вариантов);
- команда считывается из памяти и выполняется тогда, когда другим командам требуются результаты её выполнения (редукционные вычисления).
Как было сказано в одной из публикаций, размещённых на сайте habrahabr.ru, более подробная ссылка на которую будет представлена далее по тексту, любой вычислительный алгоритм представляет собой набор математических формул, по средствам вычисления которых он реализуется. Всё с той же публикации возьмём, представленную в ней для примера формулу: g = e*(a+b) + (a-c)*f, и составим блок-схему алгоритма для классического процессора со следующей структурой (упрощённой и очень условной (для примера подойдёт)):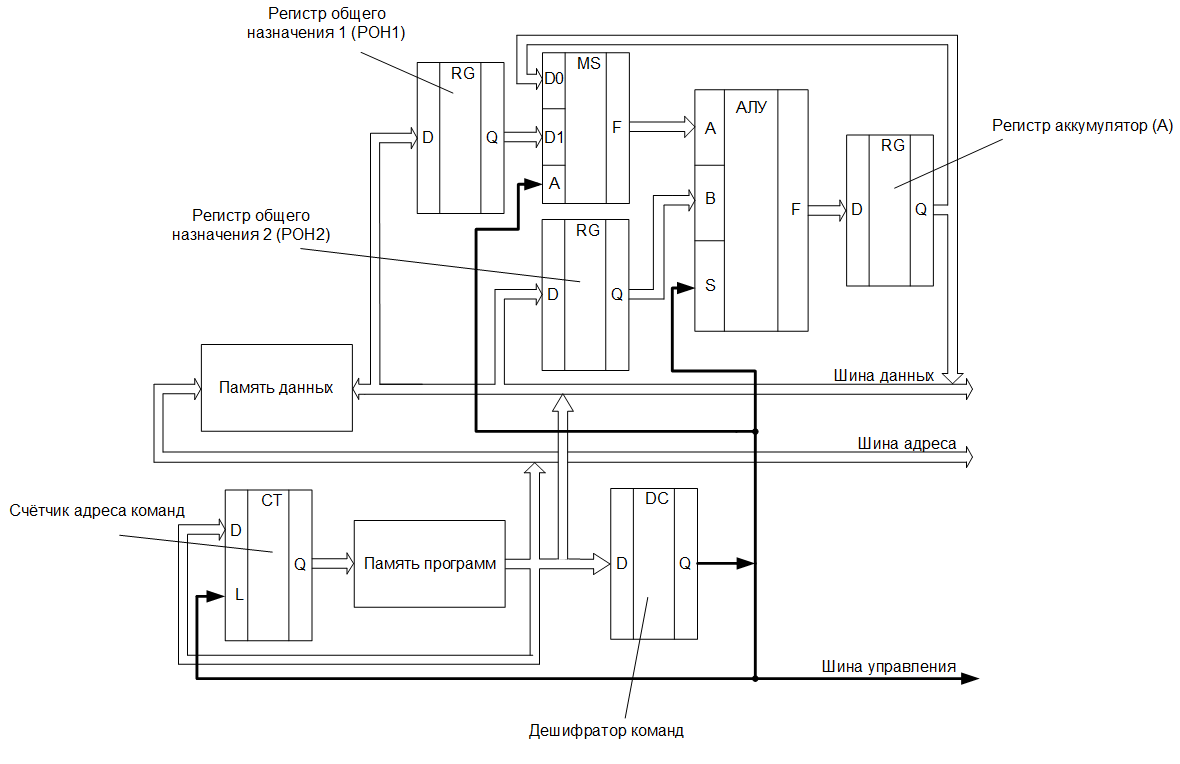
«Наш» процессор имеет гарвардскую архитектуру и состоит из двух регистров общего назначения, арифметико-логического устройства, регистра — аккумулятора, счётчика и дешифратора команд. Причём, на входной порт «А» АЛУ, может быть подано значение либо с регистра общего назначения, либо с регистра — аккумулятора. Это реализуется при помощи мультиплексора. Итак, блок-схема алгоритма для данного процессора будет выглядеть так: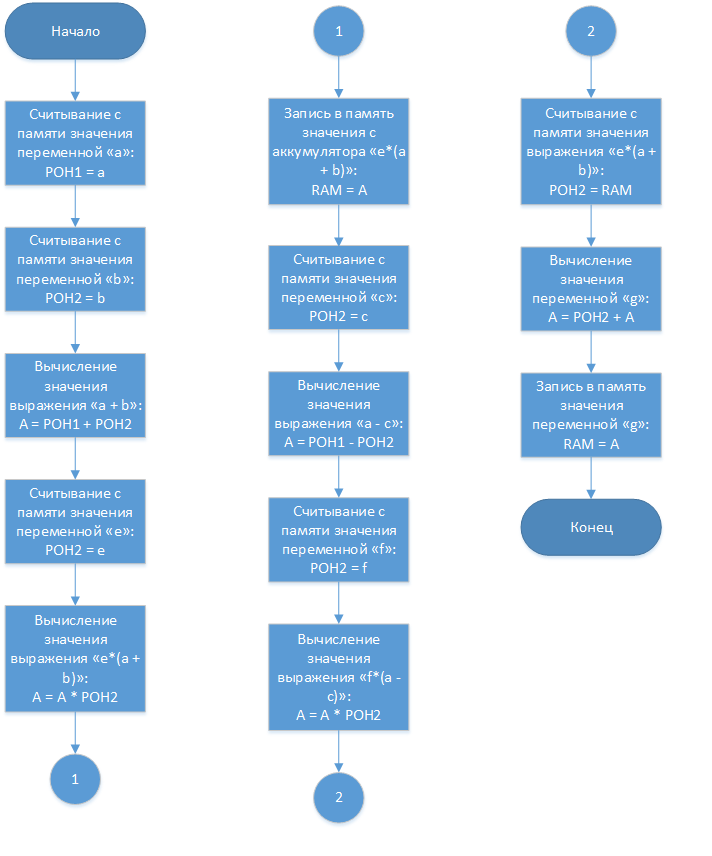
Каждый операционный блок на блок-схеме — это аналог ячейки на ленте в машине Тьюринга, а счётчик адреса команд — аналог считывающей головки. Итого, для вычисления, взятой для примера формулы, понадобится считать 13 ячеек (выполнить 13 действий).
Что же касается потоковых вычислений, то вот здесь рассказывается, что это за вычисления и как они реализуются. Для нашего случая (взятой для примера формулы), граф потоковых вычислений (аналог блок-схемы алгоритма) будет иметь следующий вид:
Для потокового процессора со следующей структурой:
вычисления с распределением команд, будут выглядеть следующим образом:
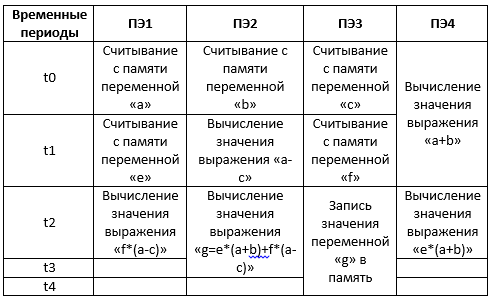
Сравнительно, не так давно, одна из отечественных компаний заявила об окончании разработки процессора с такой архитектурой. Эта компания называется ОАО «Мультиклет». В их разработке, каждый процессорный элемент называется клеткой, отсюда и название — мультиклеточный процессор. На habrahabr.ru есть множество публикаций, посвящённых этому процессору, например вот эта. Эта публикация и есть та самая, ссылку на которую я, ранее, обещал дать, и с которой для примера взял формулу и граф потоковых вычислений.
Вообще, когда ОАО «Мультиклет» заявил о разработке такой архитектуры, эта новость была преподнесена так, что я, было, подумал, что теперь на рынке вычислительных систем произойдёт революция, но ничего не случилось. Вместо этого в интернете стали появляться публикации о недостатках мультиклеточной архитектуры. Вот одна из них. Но, при всём при том, разработка получилась рабочей и конкурентоспособной.
Ещё один интересный способ организации вычислений, отличный от машины Тьюринга — редукционные вычисления. В предыдущем случае каждая команда выполняется тогда, когда доступны все её операнды, но при таком подходе может сложиться ситуация, когда результаты выполненной команды далее могут не понадобится, тогда окажется, что временные и аппаратные ресурсы были потрачены впустую. В редукционных вычислениях данный недостаток был преодолён тем, что исполнение команды инициируется запросом на её результаты. В математической основе таких вычислений лежат λ-исчисления. Для вычисления нашей формулы весь процесс начинается с запроса на результат g, который, в свою очередь, сформирует запросы на выполнение операций e*(a+b) и (a-c)*f, а эти операции сформируют запросы на вычисление значений a+b и a-c и т. д.: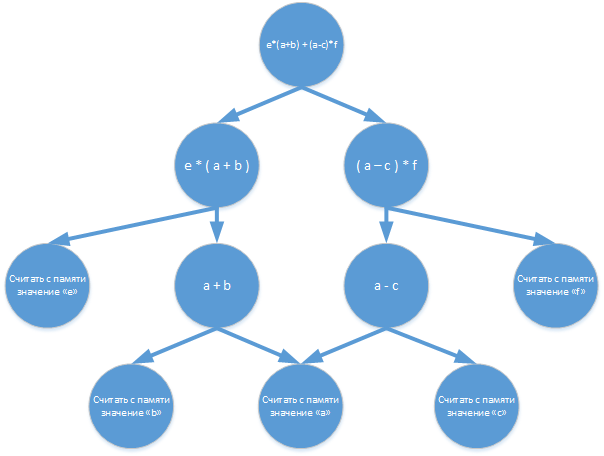
Сами по себе, редукционные вычисления состоят из процессов распознавания редексов с последующей заменой их результатами выполненных, запрошенных ранее, команд. В итоге, все вычисления редуцируются до требуемого результата. Нигде, ни в литературе, ни в интернете я не нашёл описания реальных процессоров с такой архитектурой, может плохо искал…
В настоящее время, уже ведутся исследования по созданию вычислительных систем, работающих на принципиально новых принципах, таких как квантовые вычисления, фотонные вычисления и т. д. Очевидно, что компьютеры, созданные по таким технологиям превзойдут все современные и приблизят школьников к тому моменту, когда можно будет заставить «железяку» делать за себя домашнюю работу по русскому языку. Но вопрос о создании принципиально нового способа реализации машинных вычислений, не выходя за рамки современной электроники, до сих пор остаётся актуальным.
