Математическая продлёнка. Мир треугольников
Нам то и дело приходится выступать в роли наставников. Иногда это профессия, иногда помощь своим детям, учащимся в школе или университете, а бывает так, что желание поделиться чем-то красивым с неофитами может перерасти в призвание. В любом из этих случаев нам нужны хорошие примеры. Как ведущий кружка математики для школьников средних и старших классов, я жаден до глубоких и, вместе с тем, простых для понимания примеров, дающих ключики к важным математическим концепциям. Яков Перельман уже весь в оперативке, Мартин Гарднер — тоже. Слава богу, в наше время появились великолепные Youtube-каналы (Mathologer, Numberfile, 3Blue1Brown, Aleph0, а также авторские каналы сильнейших математиков нашего времени), но отыскивать новые интересные задачи-исследования, доставляет такую радость, что грех этим не поделиться.
В этой серии заметок я привожу примеры таких маленьких учебных исследований. Их цель не «открыть новый взгляд» или не «потрясти основы», а показать привычные «школьные» математические концепции с несколько непривычных позиций, так, чтобы они, с одной стороны, стали интереснее и глубже, а с другой, чтобы с их помощью познакомить школьников, уже увлечённых математикой, с некоторым повседневным инструментарием профессионалов.
Сегодня речь пойдёт о треугольниках, о пространствах, о треугольных координатах, о симметрии и совсем немножко о мере на множестве. Основной же темой рассказа будет факторизация множеств и пространств. Мы построим и исследуем пространство треугольников. Оно очень простое, но последовательно изучить его, полезно, поскольку если кто‑либо из ребят выберет себе путь в жизни, связанный с математикой или физикой, то ему придётся иметь дело с пространствами куда более сложными и трудно представимыми. Так что хорошо бы приобрести кое‑какую интуицию, оперируя чем‑нибудь простым.
Как-то на занятии в маткружке ученица Ася сказала, что ей кажется, что равнобедренных треугольников, в каком-то смысле, меньше, чем других, но она не может точно сказать, что бы это значило. Я задумался о том, как можно было бы порассуждать на эту тему осмысленно и с пользой, и после перемены мы все вместе принялись рисовать карту мира треугольников. Потом, оказавшись дома, я стал искать материал по этой теме и наткнулся на статью Иэна Стюарта Why Do All Triangles Form a Triangle?, опубликованную в 2017 году в ежемесячнике The American Mathematical Monthly.
Стьюарт хорошо известен любителям и профессионалам математикам своими математическими очерками в Scientific American, популярными книгами «Значимые фигуры. Жизнь и открытия великих математиков», «Случайный бог или божественная случайность», «Укрощение бесконечности», а также соавторством в серии книг о Флатландии. В статье, посвящённой треугольникам, Стюарт приводит результат, подобный тому, что получили мы с ребятами на уроке. Так что на следующем занятии мы не просто вернулись к исходному вопросу, но и посмотрели на то, как на него отвечают математики-профессионалы, познакомились с привычными для них, но новыми для школьников понятиями, которые используются в статье.
Треугольники образуют множество, которое можно разделить на отдельные подмножества, используя такие характеристики, как «прямоугольные», «остроугольные», «равнобедренные» и так далее. На странице англоязычной Википедии приводится исчерпывающая диаграмма, показывающая на языке множеств, какими бывают треугольники и как соотносятся между собой их подмножества:

Различные разбиения множества треугольников на подмножества.
Эта диаграмма по‑своему остроумна, как минимум тем, что подмножества треугольников представлены их характерными элементами. Но она, к сожалению, не только не позволяет ответить на поставленный вопрос, но и сбивает с толку, давая качественно неверное представление о том, как именно классифицируется множество треугольников. Впрочем, эта диаграмма выжимает максимум из понятия «множество», которое уже знакомо школьникам. На большее этот «мешок с объектами» не способен, и для полноценной работы с мысленными моделями мира, которыми оперирует математика, этого уже недостаточно.
От множества переходим к фактормножеству
Понятие «множество» даётся как одно из фундаментальных понятий, но оно, само по себе, такое общее, что школьники с трудом могут объяснить зачем оно им нужно, и что с помощью множеств можно сделать такого, чего было бы невозможно без них. Разделив множество треугольников на подмножества, мы, конечно, кое‑что поняли, и лучше разобрались в том, как они соотносятся друг с другом с точки зрения отношения «включения», но нам хотелось более точного понимания структуры множества треугольников. Для этого нам нужны отношения между элементами множества. И самым главным в сегодняшнем рассказе будет отношение эквивалентности.
Обратим внимание вот на какое обстоятельство: Треугольники могут не только отличаться друг от друга, но и быть одинаковыми.
Вспомните признаки равенства треугольников, согласно им, два треугольника, не зависимо от того как они расположены в пространстве, при определённых условиях, могут считаться одинаковыми. У них будут равные площади, периметры, особые линии (медианы, высоты и т.п.), а при наложении одного треугольника на другой, совпадут все их точки, так что эти две фигуры станут неразличимы. Такое отношение называется конгруэнтностью.
Это наблюдение позволяет нам говорить не о всех треугольниках на свете, а о более абстрактном множестве уникальных треугольников, в котором нет двух конгруэнтных фигур. Каждому элементу из него соответствуют все равные ему треугольники, как бы они ни были расположены или повёрнуты в том геометрическом мире, в котором они могут появиться. В евклидовом пространстве все точки конкретного треугольника принадлежат одной плоскости, а это значит, что среди любых треугольников, нарисованных ли в тетрадке, висящих ли в пространстве, неважно, трёхмерном или десятимерном, есть конгруэнтные и неконгруэнтные. Поскольку можно движением совместить как плоскости, в которых лежат треугольники, так и сами фигуры.
Итак, коль скоро «место обитания треугольников» нас не интересует, мы можем «вынести его за скобки». Такой мысленный приём называется факторизацией. Для факторизации нужно определить какое-то отношение эквивалентности, то есть способ показать, что некие два элемента в каком-то смысле, равны, неразличимы. После этого, мы можем слить все одинаковые элементы в один новый объект, который называется классом. Отношение эквивалентности позволяет разделить все множество на классы так, чтобы у них не было перекрытий и не оставалось лишних элементов. То есть, чтобы каждый элемент множества оказался ровно в одном классе. Факторизацию можно представить так: «раскладываем» все одинаковые треугольников «по стопкам», после чего, из каждой стопки берём только по одному образцу. Множество таких образцов будет называться фактормножеством.
Для того, чтобы любой элемент из класса имел полномочия образца, необходимо, чтобы отношение эквивалентности было организовано правильно. В частности, важно, чтобы эквивалентность «передавалась» по цепочке. То есть, из того, что эквивалентно
и
эквивалентно
должно следовать, что
эквивалентно
Это не просто формальное занудство. Вот пара примеров отношений, похожих на равенство, но не являющихся эквивалентностью: для числовых величин — »примерно равно» или »равно с точностью до 1%», для геометрических фигур — »касаться» или »пересекаться».
Легко убедиться в том, что конгруэнтность это хорошее отношение, которое вполне годится для разбиения множества фигур на классы эквивалентности.
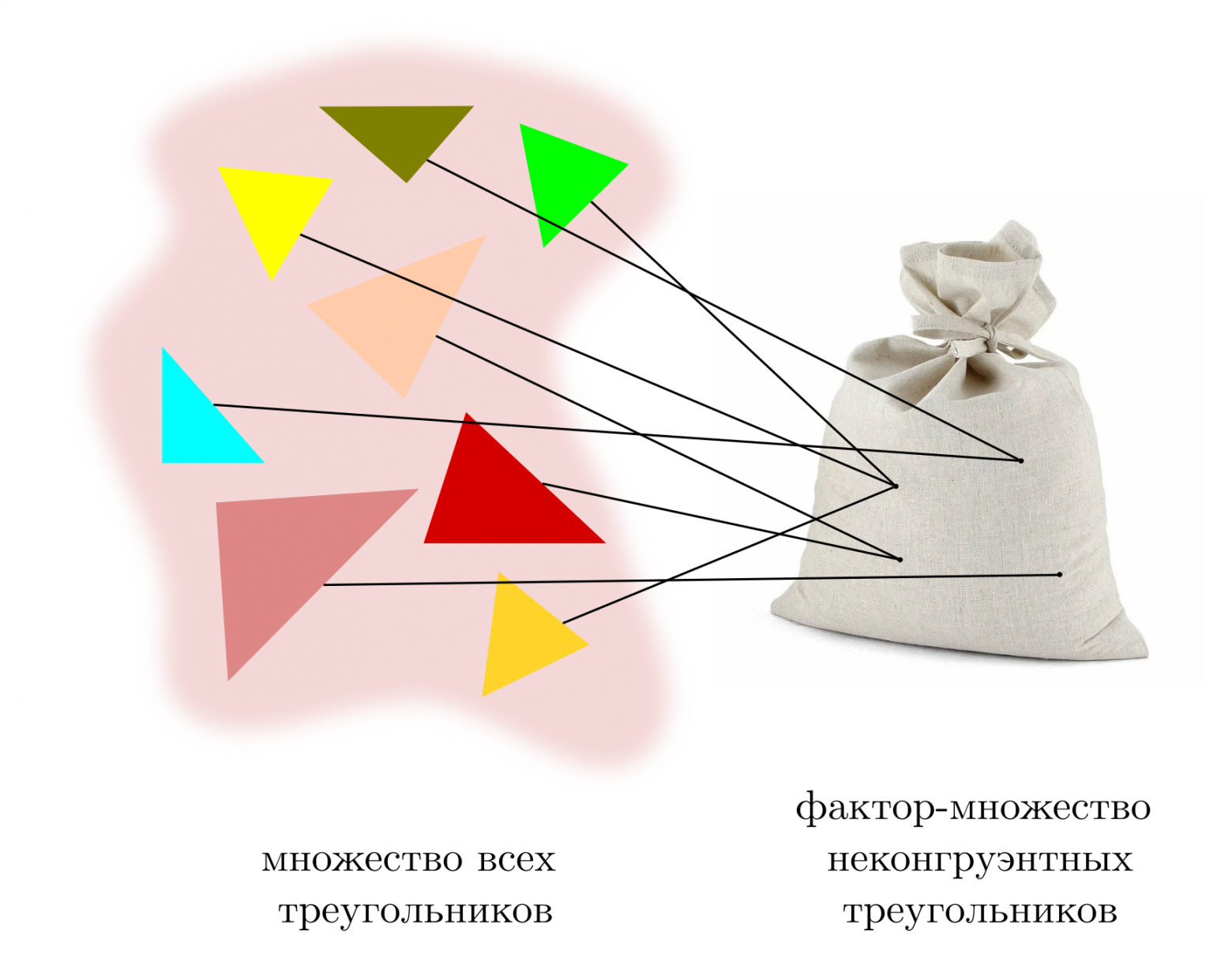
Факторизация множества треугольников отношением конгруэнтности.
Итак, всё мыслимое разнообразие треугольников, которое можно нарисовать на доске, в тетрадке или даже расположить в каком-либо объёме, мы факторизовали с помощью отношения равенства и сосредоточились на фактормножестве уникальных, неравных между собой треугольников. Если мы обозначим множество треугольников буквой , то множество, факторизованное отношением конгруэнтности
будет обозначаться так
От фактормножества переходим к пространству
Треугольники могут быть не только равны или не равны, но и похожи друг на друга. Причём, похожи они бывают настолько, что становятся практически неотличимыми. Можно говорить о почти равностороннем треугольнике или почти прямоугольном, имея в виду, что отличие от истинно равностороннего и прямоугольного, в каком-то смысле, незначительно. Для любого треугольника можно рассмотреть целое множество треугольников «похожих на него», мысленно окружив его своеобразным «облаком» почти‑двойников.
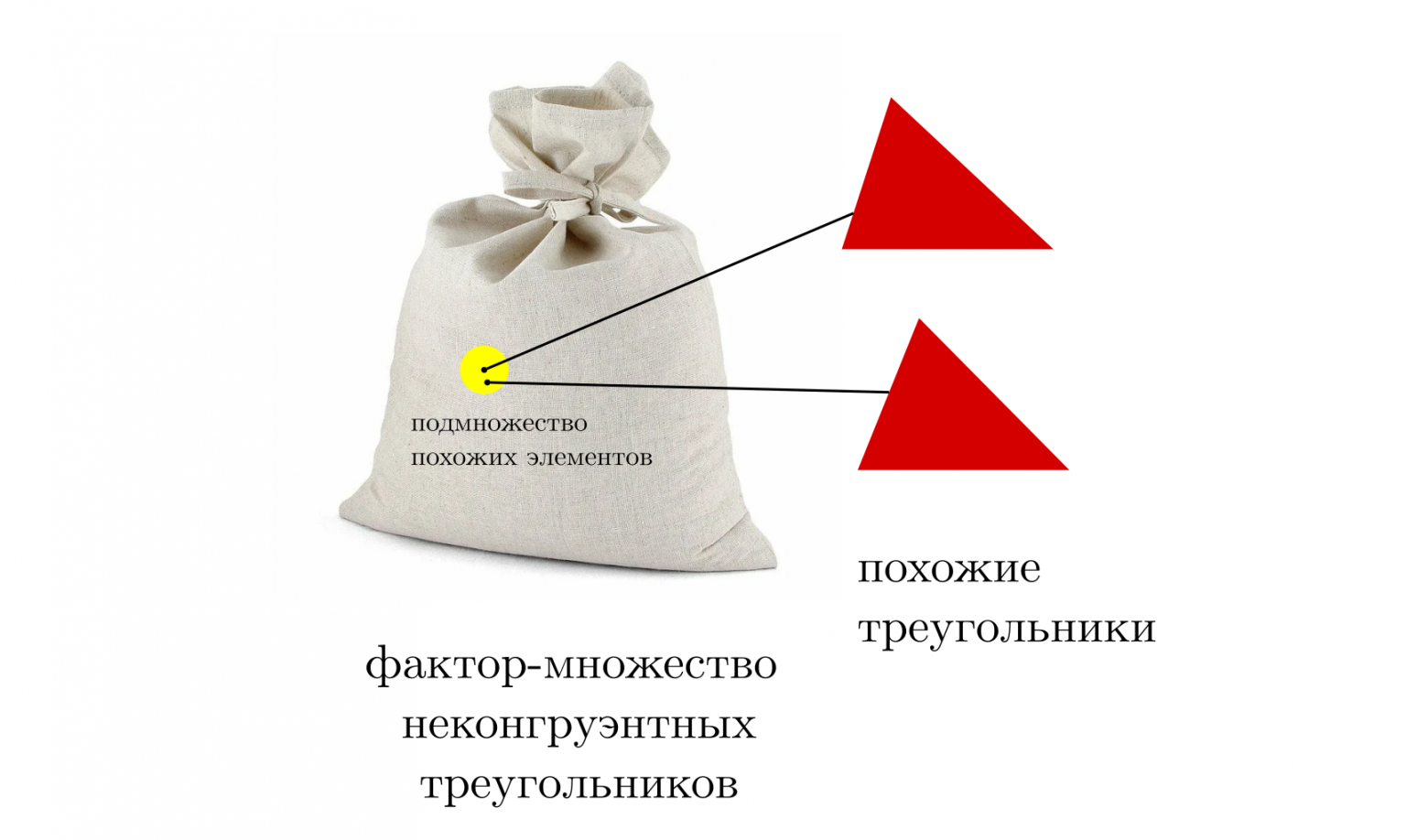
Отношение эквивалентности позволяет нам разбивать множество на классы и выявлять некую внутреннюю структуру множества. Как мы уже упоминали, отношение »примерно равно» не является эквивалентностью. Однако с его помощью мы можем построить систему открытых подмножеств (тех самых «облаков» похожих друг на друга элементов), такую, что их пересечения и объединения тоже будут формировать открытые подмножества, способные покрыть всё множество треугольников.
Это обстоятельство позволяет нам говорить о множестве треугольников, как о топологическом пространстве, каждый элемент (точка) которого соответствует какому-то уникальному треугольнику. От простого множества пространство отличается тем, что для него определена топология — формальная система открытых подмножеств, замкнутая относительно объединения и пересечения.
Нам сейчас нет необходимости влезать в формальную сторону топологии, оставим это до университетского курса. Важно почувствовать, какой смысл мы вкладываем в это слово «пространство». Это множество объектов, позволяющее нам рассуждать о таких его характеристиках, как размерность, связность, непрерывность, рассматривать подпространства (аналоги подмножеств), области и их границы, строить пути между точками и даже говорить о дырках. Евклидово геометрическое пространство, в котором мы обычно строим треугольники на уроках в школе, это тоже пример топологического пространства, но оснащённого дополнительными свойствами, позволяющими рассуждать о расстояниях между точками и углах между прямыми.
Говоря о пространстве вне математики, мы обычно имеем в виду некое вместилище объектов, или пустую сцену, на которой они размещаются. И в рамках школьного курса, когда мы рассуждаем о геометрии, простейшие элементы пространства, которые мы называем точками, как‑то размещаются в нём и образуют множества с точно определёнными свойствами, которые мы называем геометрическими фигурами. Исследуем мы при этом фигуры, а само по себе пространство пусто, и единственное, что мы от него требуем, это возможности рассуждать о таких отношениях между точками и фигурами как «внутри‑снаружи», «близко‑далеко», «выше‑ниже» и т. п.
Треугольники, о которых идёт речь в этой заметке, это фигуры, определённые в каком‑то геометрическом пространстве. Но последнее мы «вынесли за скобку» при факторизации. Что же мы имеем в виду, говоря о «пространстве треугольников» ? Оно не имеет никакого отношения к тому, где располагаются сами треугольники. Это пространство не часть плоскости, или какой-то поверхности, а самостоятельный математический объект. Каждая точка в этом пространстве соответствует какому-то треугольнику.

Меняем лексику, переходя от множества к пространству.
Определяем размерность пространства треугольников
Одна из самых главных характеристик топологического пространства — его размерность. Точное определение топологической размерности мы, опять же, оставим до университетского курса, и постараемся определить какова размерность пространства треугольников, исходя из самых общих соображений.
Можно ли нарисовать и увидеть математически идеальную линию, не имеющую ширины? А точку, которая, согласно определению Евклида, не имеет ни ширины, ни длины, и никаких составных частей? Вполне!
Наш глаз видит области и их границы. Линия — это граница области, а точка — это граница линии. Мы прекрасно видим как одна область граничит с другой, мы видим эту границу, но она не имеет ширины. В принципе не имеет! Как ни увеличивай участок границы, хоть до пикселей, хоть до фотонов, мы сможем сказать: «Вот одна область, а вот другая, а то что между ними — граница». И точки, абстрактные, математически точные, мы тоже в состоянии и изобразить и увидеть. Это «места», в которых встречаются границы трёх областей или в которых нарушается гладкость линии.

Идеальные лини и точки, как границы подпространств.
Визуализировать пространство мы пока не в состоянии, однако мы можем определить его размерность умозрительно, так сказать, «наощупь». От понятия размерности нам потребуется только свойство, которое очень легко проиллюстрировать в окружающем нас мире:
Размерность области на единицу больше размерности её границы.
Давайте ещё раз перечислим классы треугольников и топологические отношения между ними, то есть, отношения подпространство/граница:

Здесь картинками условно показаны классы треугольников.
Выпишем теперь все соотношения между размерностями подпространств, соответствующих классам треугольников, выразив их через неизвестную размерность всего пространства треугольников :
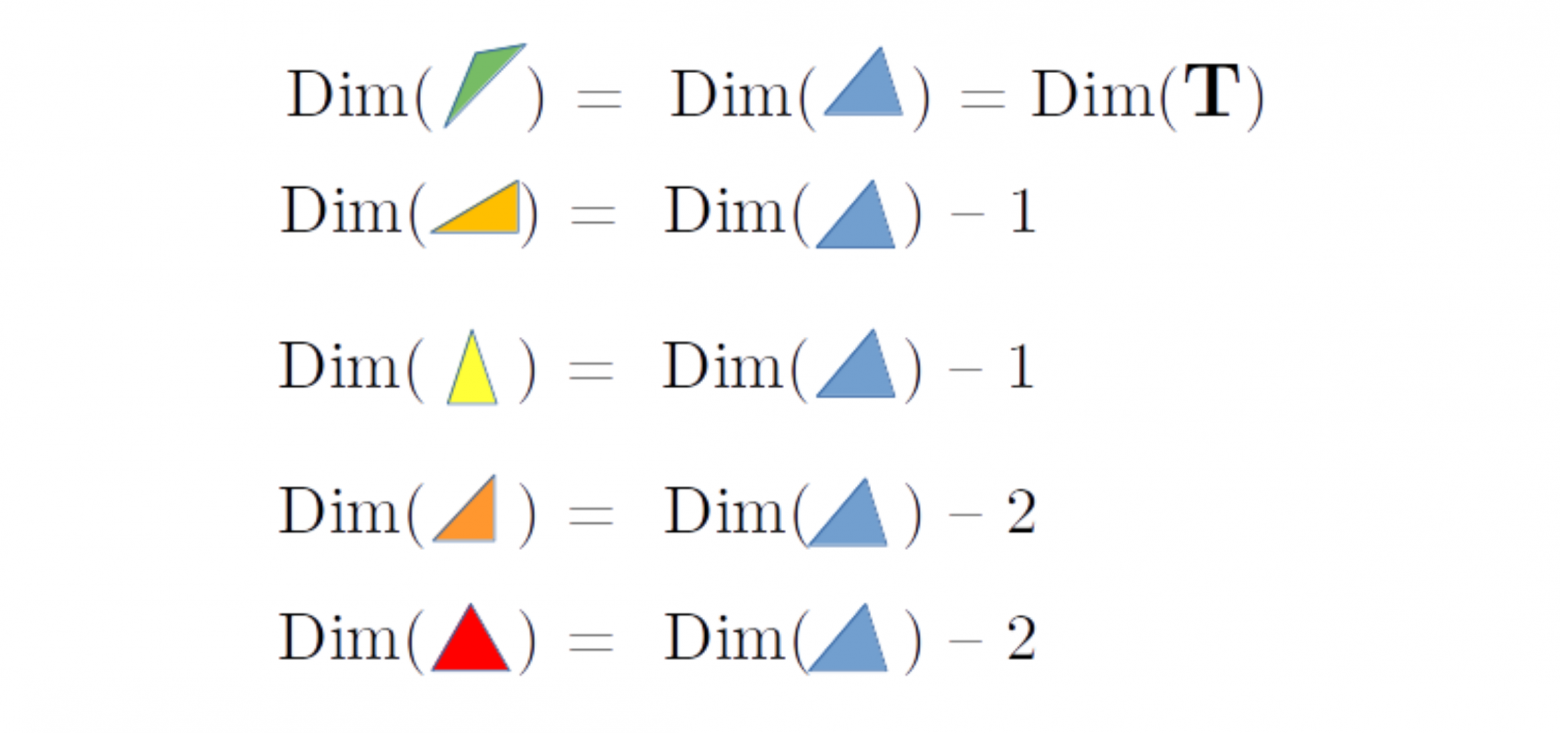
Редко когда топологии строятся или изобретаются с нуля. Один из самых распространенных на практике способов состоит в том, чтобы взять какую-то готовую, хорошо известную топологию, и построить непрерывное отображение из неё в новую. Такое отображение можно представить себе, как словарь или как рецепт, следуя которому можно по точкам одного пространства построить точки другого, причём, так, чтобы окрестности исходной точки превращались в окрестность результата отображения.
Самый привычный для нас и полезный пример хорошо изученной топологии — та, что из множества чисел строит вещественную числовую прямую. На ней хорошо определены и, главное, интуитивно понятны такие вещи, как интервал (открытый и закрытый); окрестность точки; существование непрерывного пути, соединяющего одну точку с другой, и проходящего через бесконечное множество промежуточных точек.
Аналогом этой конструкции в физической реальности можно считать ручку плавной настройки громкости или яркости. Между тремя абсолютно разными объектами и понятиями: 1) положениями ручки, 2) физическим уровнем громкости и 3) неким числом, есть прямая и понятная связь, которая и отражает то, что мы назвали непрерывным отображением. Они все имеют сходную топологию и образуют одинаковое топологическое пространство размерности 1, которое математически описывается закрытым интервалом или отрезком.
Давайте применим это соображение к объекту нашего исследования. Одна из очевидных «ручек» для настройки треугольников это их масштаб, который естественно выражается вещественным числом.
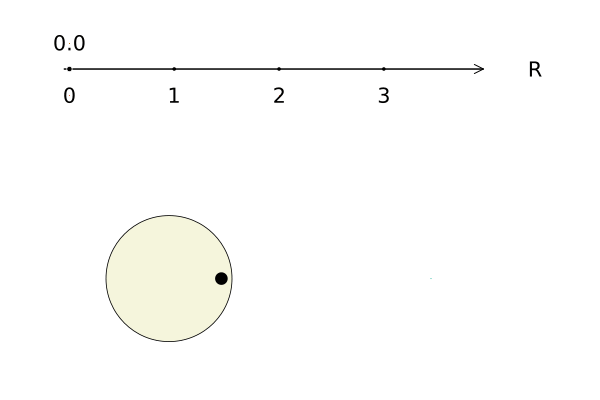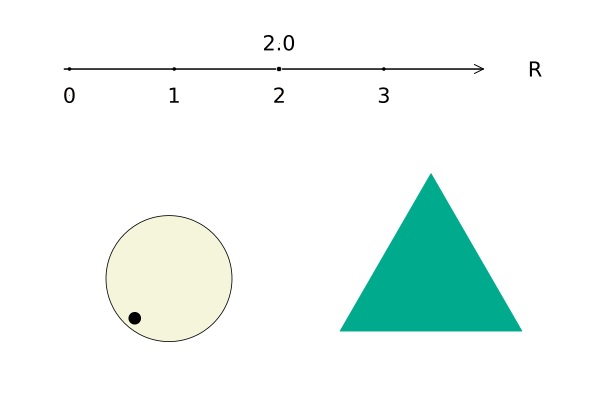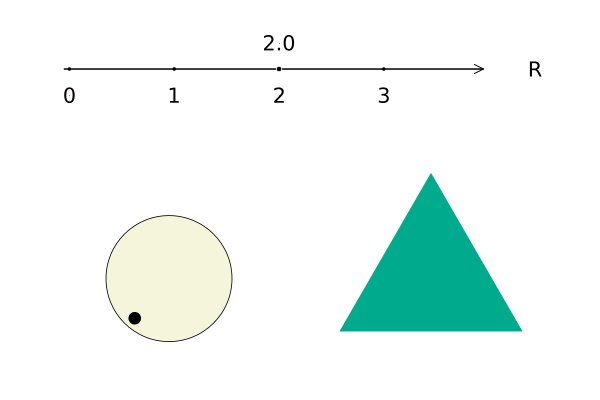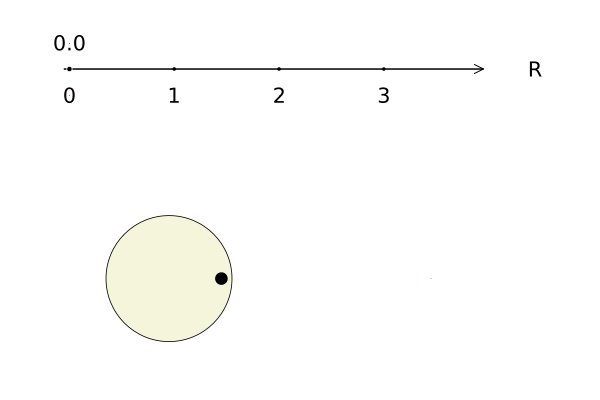
В этой картинке целых пять пространств с эквивалентными топологиями: 1) вещественные числа, 2) точки на вещественной прямой, 3) повороты «ручки», 4) масштаб треугольников и 5) время.
Это значит, что все равносторонние треугольники, не равные друг другу, отличаются только масштабом, и образуют одномерное подпространство. Отсюда мы можем вывести размерности всех прочих подпространств, и прийти к выводу, что размерность пространства треугольников, факторизованного отношением конгруэнтности равна трём.

Какой смысл говорить о трёхмерности абстрактного и невидимого пока пространства ? Вспомним классические признаки равенства треугольников. Во всех этих признаках фигурируют какие-нибудь три числовых характеристики фигуры:
● сторона, сторона, угол;
● сторона, угол, угол;
● сторона, сторона, сторона;
● сторона, угол, площадь;
● площадь, угол, периметр.
Каждую из этих характеристик можно топологически представить интервалом («ручкой»). При этом хотя бы одна из этих характеристик должна задавать масштаб или размер треугольника. Как правило, в роли этой характеристики выступает сторона, но её роль может сыграть периметр, площадь или скажем, среднее геометрическое сторон треугольника.
Говоря об этих параметрах, можно вспомнить ещё один термин, помогающий характеризовать размерность пространства: количество степеней свободы, или количество числовых параметров, однозначно определяющих точку пространства. У произвольного треугольника три степени свободы — мы их перечислили. У равнобедренного — две, ими могут быть, например, длина основания и угол при вершине. У прямоугольного треугольника тоже две степени свободы: пара катетов, гипотенуза и один из углов… Наконец, равносторонний и равнобедренный прямоугольные треугольники имеют лишь одну степень свободы — масштаб.
Если параметризовать треугольники тремя сторонами, то можно получить три независимые оси, задающие «координаты», позволяющие вложить пространство треугольников в привычное нам трёхмерное евклидово пространство. Дальше можно попытаться как-то визуализировать подпространства остроугольных и тупоугольных треугольников и их границы, но это существенно отвлечёт нас от основной темы (топологические пространства и факторизация) и потребует экскурса в элементы линейной алгебры, конических сечений, или элементов проективной геометрии.
К тому же, живя в трёхмерном мире, по-настоящему видеть его мы не можем. Наши глаза способны выделять двумерные границы трёхмерных подпространств, а также их границы: линии и точки. Так что показывать и анализировать существенно трёхмерные объекты без привлечения анимации непросто. Мы избавимся от трёхмерности пространства избрав вместо конгруэнтности другое отношение эквивалентности — подобие.
Классификация треугольников (правильный, равнобедренный, прямоугольный и т.д.) не зависит от их масштаба. Таким образом, если одной из «ручек», использованных нами для построения трёхмерного пространства треугольников, будет их линейный масштаб, то при вращении этой ручки, структура пространства, то есть число областей, их границ, и то как они граничат друг с другом, изменяться не будет. Получается, что одно измерение у нас «лишнее» и не несёт информации о структуре пространства. Если мы сочтём неразличимыми все подобные треугольники, то про их размеры можно будет забыть, и сосредоточиться только на форме. При этом точкой в факторпространстве, построенном с помощью отношению подобия, будут совокупности всех подобных друг другу треугольников.
Это пространство двумерно. Поскольку все равносторонние треугольники подобны, они факторизуются в единственную точку нулевой размерности. Пересчёт размерностей покажет, что равнобедренные и прямоугольные треугольники образуют одномерные подпространства, ограничивающие двумерные области остроугольных и тупоугольных треугольников.
Треугольные координаты
Двумя параметрами, характеризующими треугольник и весь класс подобных ему, могут быть либо пара отношений сторон, либо пара углов, либо пара из отношения сторон и угла. Углы мне нравятся больше всего, во-первых, тем, что диапазон их изменений конечен, а во-вторых, чудесным свойством давать для любого треугольника в сумме 180°. Можно было бы использовать эти два угла, как обычные прямоугольные координаты для нашей карты, или даже как угловые координаты на сфере, построив шикарный глобус треугольного мира, но коль скоро речь зашла о треугольниках, я решил показать ребятам необычные, но очень подходящие треугольные координаты.
Есть у равностороннего треугольника одна интересная особенность. Выберем произвольную точку внутри него и проведём три луча, параллельных сторонам треугольника, как показано на рисунке. Границы треугольника отсекают на этих лучах три отрезка. Так вот, сумма длин этих отрезков всегда равна длине стороны треугольника. Доказывается это утверждение без слов, в духе древних: «Смотри!», достаточно отметить на чертеже отрезки равные между собой из соображений параллельности, чтобы убедиться в его справедливости.
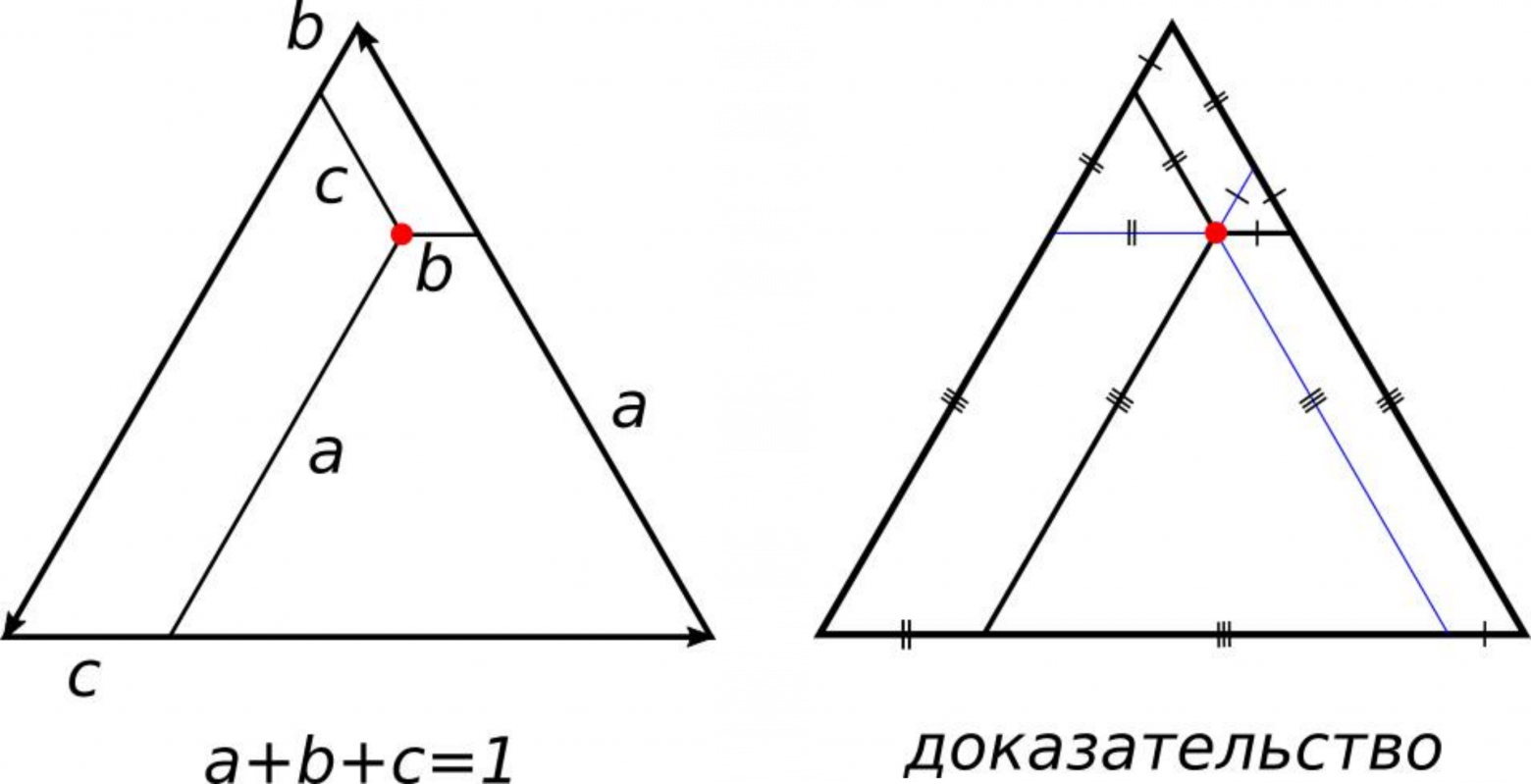
Эта теорема превращает треугольник в любопытный и полезный инструмент. Если мы разметим стороны треугольника одинаковыми линейными шкалами (они условно показаны стрелочками), то у любой точки в треугольнике появятся координаты. Причём, сумма этих координат всегда постоянна и равна максимальной отметке шкалы. Построенная таким образом диаграмма может быть полезна для изображения и анализа трёхкомпонентных смесей. Доли компонент в общем объёме в сумме всегда дают единицу, и треугольные координаты точек тоже обладают таким свойством. На треугольной диаграмме невозможно отобразить некорректную смесь, зато любая корректная смесь имеет свою точку в треугольнике и наоборот. На математическом языке мы скажем, что треугольные координаты определяют изоморфизм между точками внутри треугольника и составами трёхкомпонентных смесей.
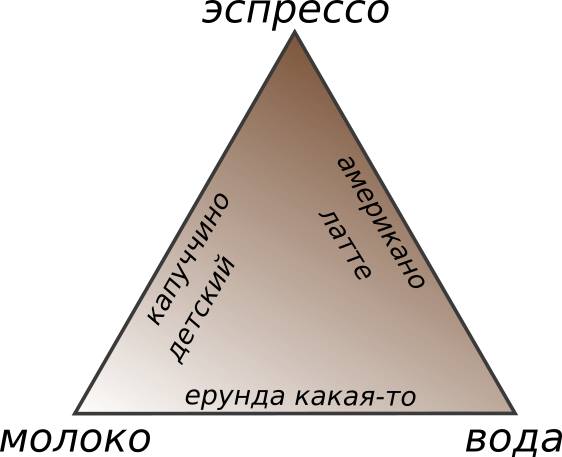
Диаграмма кофейных смесей
Петрологи рассматривают на треугольных диаграммах семейства полевых шпатов и шпинелей; металлурги рисуют на них сплавы и так далее. Все видели цветовой треугольник, который используется для выбора цвета в графических редакторах. Мы с ребятами разместили на треугольной диаграмме любимые виды кофе, собирая их из эспрессо, молока и воды.
Главное свойство треугольных диаграмм состоит в том, что, хотя они двумерны, у всех точек на ней по три координаты, связанные простым условием: сумма координат для всех точек диаграммы должна быть одинакова. Мы исследуем треугольники и тремя компонентами в этом случае могут служить три угла треугольника, которые в сумме всегда дают развёрнутый угол. Выходит, треугольные координаты идеально подходят для изображения карты треугольников, какое чудесное совпадение! По осям мы отложим все возможные значения углов, так что на такой диаграмме можно будет найти треугольник любой формы.

Равносторонний, равнобедренные и прямоугольные треугольники в треугольных координатах.
В центре мира расположился единственный (с точностью до размеров) равносторонний треугольник с координатами . Всякий равнобедренный треугольник имеет координаты
, которые ложатся на медианы треугольника. Прямоугольные треугольники привязаны к координате 90° и совпадают с координатной сеткой. И вот перед нами ландшафт страны, которую населяют треугольники.

Ровно в середине — единственный и неповторимый равносторонний треугольник, от него в шесть сторон расходятся тонкие хребты равнобедренных, а треугольная граница, вдоль которой расположились прямоугольные треугольники, ограничивает страну остроугольных от диких тупоугольных степей убегающих до горизонта вырожденных треугольников. Мир треугольников незамкнут, его внешняя граница отсутствует, поскольку те треугольники, что пытаются достичь края своего мира, истоньшаются и вырождаются, превращаясь в отрезки, которые мы треугольниками уже не считаем. Очень здорово гулять по этой карте, переходя из страны в страну, приближаясь к границам и представляя, как меняются её жители.
На карте хорошо видны все отношения между классами треугольников. Они не образуют иерархию вложенных подмножеств, как иногда показывается на страницах учебников, а формируют области, граничащие друг с другом. Равнобедренными могут быть как остроугольные, так и тупоугольные треугольники. Прямоугольные треугольники могут быть равнобедренными, они живут там, где пересекаются линии равнобедренных и прямоугольных треугольников. Ну, а равносторонний треугольник является одновременно равнобедренным и остроугольным.
Факторизуем дальше!
Карта наша вышла очень симпатичной, но отказавшись от конгруэнтности и перейдя к отношению подобия, мы сделали её избыточной. У типичного жителя этого мира все три угла различны, обозначим их тройкой Всячески поворачивая и отражая треугольник, мы сможем получить пять его эквивалентов:
и
Все эти шесть вариантов (перестановок из трёх элементов) тоже можно найти на карте, они отражены в шести разных точках, но ведь все соответствующие им треугольники конгруэнтны.
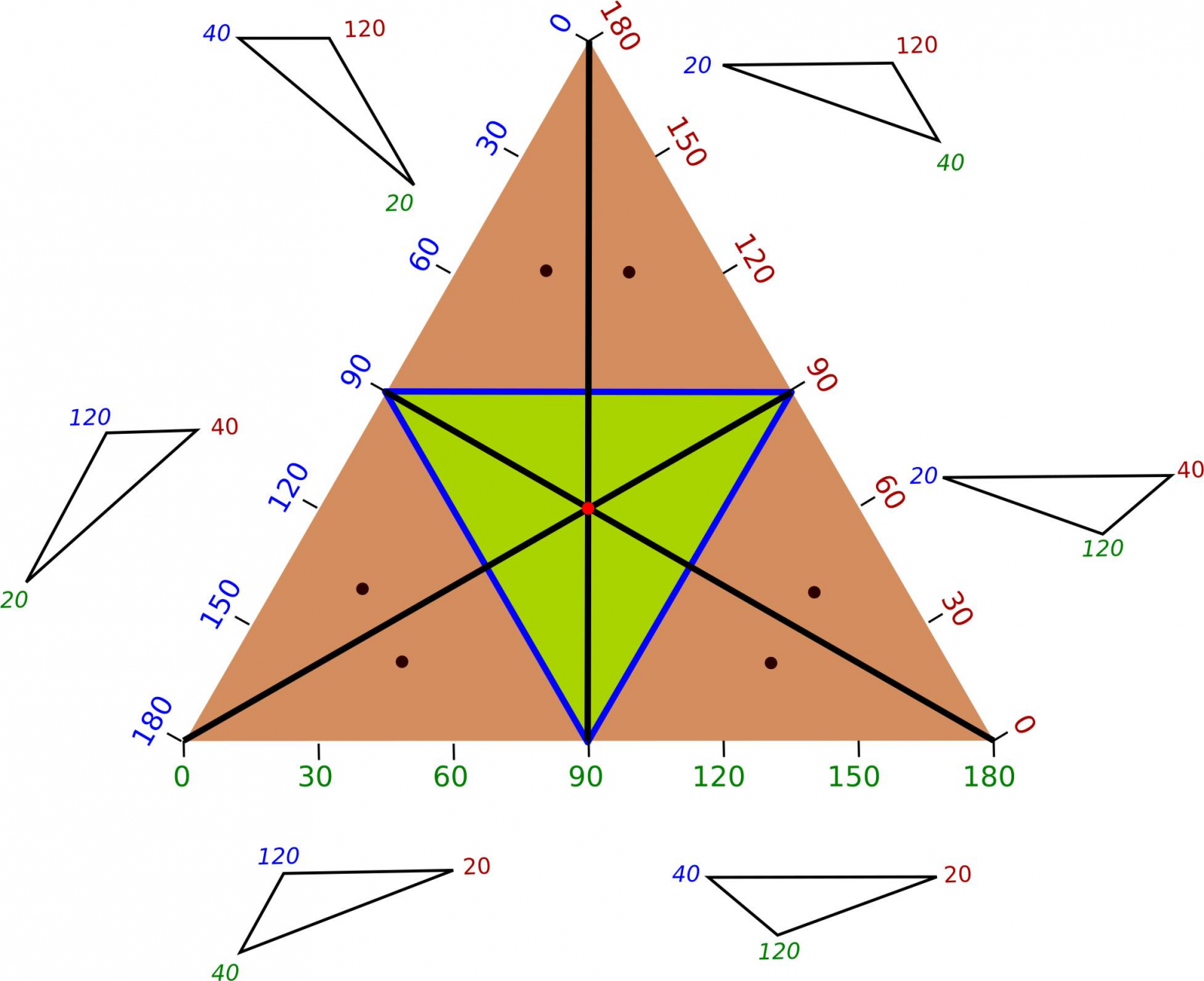
Шесть точек, соответствующих одному и тому же треугольнику (с точки зрения конгруэнтности).
Получается, что двумерное факторпространство треугольников похоже на зеркальный калейдоскоп, в котором каждая точка повторяется шесть раз. От одного варианта к другому можно перейти, комбинацией поворотов или отражений всей карты. Впрочем, не каждая точка имеет пять отражений. Равнобедренные треугольники не меняются при зеркальном отражении относительно высоты, опущенной из вершины, и поэтому имеют меньше эквивалентов. Например, равнобедренный треугольник имеет только два эквивалента:
и
получаемых поворотами на 120°. Линии равнобедренных треугольников на карте тоже не меняются при отражениях, но переходят друг в друга при поворотах. Наконец, самый симметричный равносторонний треугольник переходит сам в себя и при повороте на 120° и при отражении, также как соответствующая ему точка на карте.
Это очень красиво: симметрия карты и её элементов в точности отражает симметрию треугольников, соответствующих этим элементам! Связана эта красота с тем, что элементы пространства, то есть, точки, сами обладают определённой структурой —, а именно, симметрией. Преобразования из группы симметрии, действуя на элементы пространства, порождают орбиты этих элементов: такие множества точек, которые не меняются под действием этих преобразований.
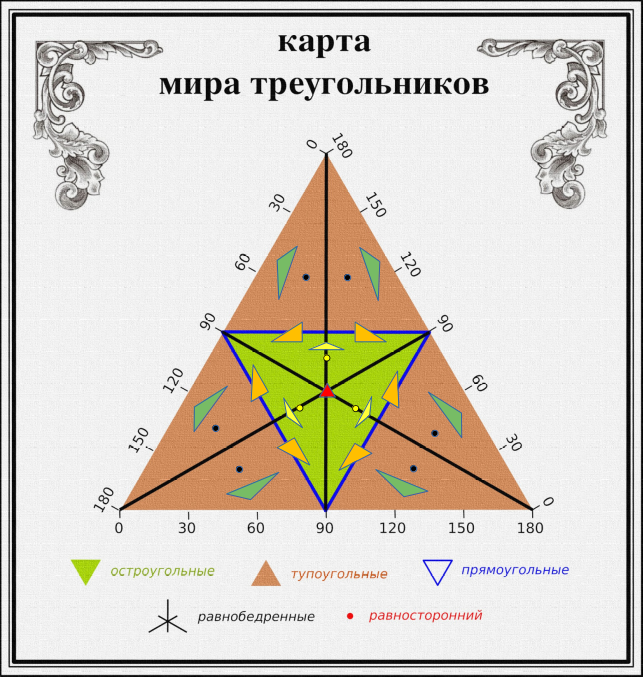
Некоторые орбиты на карте мира треугольников.
Мы могли бы избавиться от этой избыточности, если бы нам удалось факторизовать эту карту, «вынеся за скобки» её симметрию. Это можно сделать геометрически, если сложить карту, нарисованную на бумажном листе так, чтобы все эквивалентные точки наложились друг на друга и совпали. В результате получится маленький фрагмент в форме прямоугольного треугольника. Он лишён многократного дублирования точек и представляет уже факторизацию пространства треугольников отношением эквивалентности, заданным группой симметрии (эквивалентными при этом считаются все точки одной орбиты).
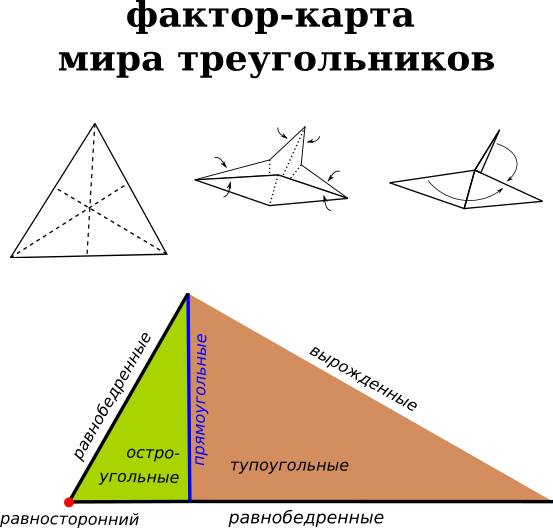
Построение фундаментальной области фактор-пространства треугольников.
Такая сжатая фактор-карта не избыточна, оставаясь полной. На ней каждая точка — уникальный треугольник и каждому треугольнику полагается уникальная точка. Она даёт исчерпывающее представление о структуре классификации треугольников. В топологии такая факторизация называется выделением фундаментальной области. Группа симметрии треугольника, действуя на эту область, формирует всё рассматриваемое нами пространство.
Когда мы абстрагируемся от симметрии треугольников, форма фундаментальной области не играет никакой роли и то, что она у нас оказалась треугольной, связано только с произвольным выбором треугольной системы координат. Так что правильнее будет изобразить фундаментальное множество фактор-пространства треугольников в такой обобщённой форме:

Топология фундаментального множества пространства треугольников, факторизованного отношением подобия.
Топология этого фундаментального множества соответствует диску, границей которого являются равнобедренные треугольники. На эту границу можно гладко отобразить одномерный интервал, соответствующий углу при вершине этих треугольников. Прямоугольные треугольники разделяют этот диск на области остроугольных и тупоугольных треугольников. Все вырожденные треугольники, составлявшие открытую границу карты мы отобразили в точку, выколотую из границы диска.
Отмечу здесь в скобках, что топология фундаментального множества (диск с выколотой точкой на границе) оказалась существенно более вразумительной, чем у треугольной карты, на которой все точки границы отождествляются друг с другом нетривиальным образом. Искушённые в топологии читатели распознают в ней вещественную проективную плоскость, безусловно, интересную, но крайне неинтутивную поверхность, которая не имеет не самопересекающихся вложений в трёхмерное пространство. При попытке натянуть пространство треугольников на глобус, используя сферические угловые координаты, и отождествление вырожденных треугольников тоже приводит к вещественной проективной плоскости.
На протяжении этой статьи мы неявно использовали предельную степень факторизации множества треугольников, разделив их на шесть классов, которые изображали с помощью маленьких разноцветных треугольничков-представителей. Если мы введём несимметричное отношение »быть границей», то с его помощью сможем изобразить структуру мира треугольников в виде ориентированного графа:
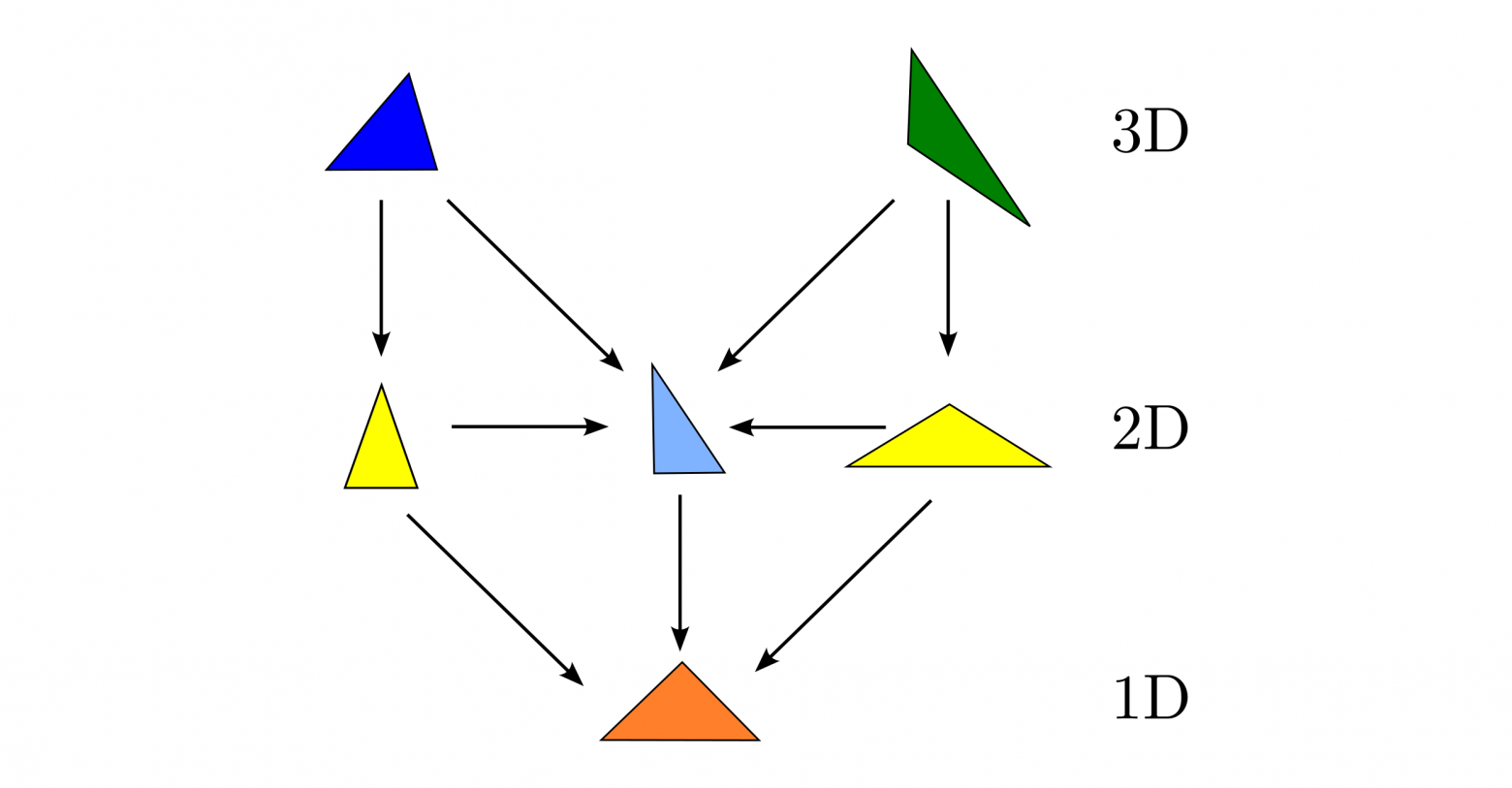
Стрелки здесь указывают на границы объектов.
При этом теряется визуальный образ фундаментальной области, но остаются хорошо видны взаимоотношения между классами треугольников.
Измеряем то, что можем
Имея перед собой структуру треугольного мира, очищенную от повторений и многократных отражений, мы, наконец, готовы подумать над вопросом ученицы Аси: каких треугольников больше — равнобедренных или обыкновенных. Считать сами точки на карте дело неблагодарное. Вместо этого следует сделать наше пространство измеримым, введя на нём корректную меру. Я не буду сейчас приводить полное строгое определение меры и положусь на наше с вами интуитивное понимание, основанное на опыте работы с такими мерами, как длина, площадь, объём, вес, количество чего-то счётного и так далее. Пока мы не приводим контринтуитивных при
