Математическая продлёнка. Из чего сделаны Пифагоровы штаны02.04.2023 13:31

Поводом для написания этой заметки послужила новость, облетевшая мир 18 марта этого года: две школьницы из Нового Орлеана, Кальцея Джонсон и Не`Кия Джексон «впервые доказали теорему Пифагора», опираясь на теорему синусов. В России эту новость встретили с иронией и стёбом, но не бывает плохих поводов поговорить о хороших теоремах.

Одним из ключевых результатов теории категорий является осознание, что знания о каком-то объекте даёт не его «внутреняя» структура, а структура его отношений и связей с другими объектами в его категории.

В этой статье я хочу рассмотреть связи существующие между теоремой Пифагора с иными утверждениями: теоремой косинусов, теоремой синусов, евклидовостью пространства и свойствами скалярного произведения векторов. Ну, и заодно, разобрать пресловутое свежее доказательство американских школьниц, пока оно окончательно не забылось.

Существует давний «вид спорта», состоящий в поиске новых, сложных, простых, оригинальных и элегантных, доказательств великой теоремы Пифагора:

в прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы.

Отличная коллекция доказательств представлена, например, тут. Она даёт представление как о диапазоне методов доказательства, так и о неуёмности человеческого творчества. Не думаю, что какая-то ещё математическая теорема была обоснована настолько убедительно. Более ста лет назад удалось найти не просто десятки доказательств, а целые их семейства, содержащие по нескольку тысяч отдельных вариантов, а появившиеся в ХХ веке методы, использующие замощения плоскости, вообще, привели к непрерывным многообразиям доказательств.

А какие ингридиенты совершенно необходимы для того, чтобы эта чудесная теорема была доказана, и обязаны присутствовать в любом доказательстве? Например, для приготовления чашечки эспрессо требуется достаточно много необходимых вещей: кофе, вода, чашка, посуда или машина для приготовления напитка, огонь или электричество… Если исключить что-нибудь из этого списка, то и чашечка эспрессо не состоится, либо изменится до неузнаваемости.

Примеры доказательств

Начнём разговор с того, что рассмотрим несколько доказательств, практически не требующих слов и каких-либо дополнительных формул для вычисления площадей, длин и прочих величин, не относящихся к делу.

Через подобие

Моё любимое доказательство, основанное на признаке подобия прямоугольных треугольников по равенству одного из острых углов, которое, в свою очередь, опирается на то, что сумма углов в произвольном треугольнике равна развёрнутому углу. Кроме того, здесь используется принцип подобия для площади.

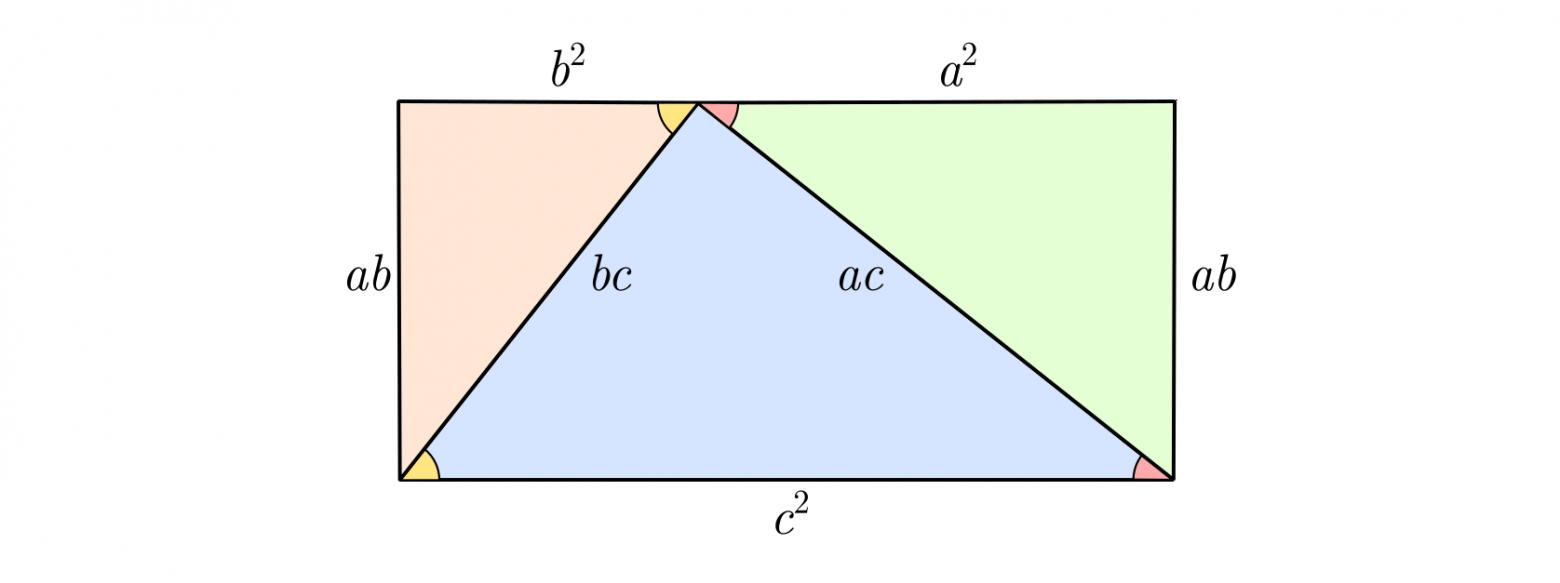
Через достраивание до прямоугольника и через длины сторон

С помощью трёх подходящим образом масштабированных подобных прямоугольных треугольников, можно построить прямоугольник, в котором стороны демонстрируют искомое равенство. Прямоугольник образуется из-за того, что сумма углов в треугольнике равна развёрнутому углу, а прямой угол является его половиной.

Через достраивание до квадрата и через площади

Очень популярное доказательство, основанное на том, что из четырёх копий прямоугольного треугольника можно сложить квадрат. Это, в свою очередь, связано с тем, что прямой угол равен четверти полного оборота. Кроме того, необходимо, чтобы сумма острых углов в прямоугольном треугольнике была равна прямому углу.

Через элементы анализа

Здесь кроме предельного перехода и формулы для производной произведения, используется подобие персикового и зелёного треугольников

Через теорему косинусов

Грамотный девятиклассник может получить теорему Пифагора с помощью теоремы косинусов, подставив в неё прямой угол. Теорема косинусов доказывается в школьном курсе совсем несложно и, как правило, доказательство опирается на уже известную ученикам теорему Пифагора и уже знакомую функцию косинус.

Но доказать её можно, используя самые минимальные средства элементарной геометрии, минуя как тригонометрию, так и теорему Пифагора. Это можно сделать, видоизменив одно из приведённых выше доказательств теоремы Пифагора, отказавшись от прямоугольности треугольника.

Рассмотрим на плоскости произвольный треугольник со сторонами a,b и c. Из трёх копий этого треугольника, пропорционально увеличенных в a,b и c раз, сложим пятиугольник ABECD, как показано на рисунке.

e4eb8f946e327195caa9960332cace7c.png

Поскольку сумма углов в треугольнике на плоскости равна развёрнутому углу, \angle DCE будет развёрнутым. В силу подобия треугольников, ∠ABC = ∠BCE,а значит отрезок DE параллелен отрезку AB. Наконец, AD = BE, по построению. Следовательно, получившийся четырёхугольник является равнобокой трапецией.

Построив высоты в трапеции, и воспользовавшись её симметрией, видим, что a^2 + b^2 = c^2 + 2x где x можно выразить через функцию от угла и длину ab. Эту функцию угла, являющуюся коэффициентом пропорциональности между гипотенузой и катетом, прилежащим к углу мы и называем косинусом.

Если исходный треугольник будет тупоугольным, ничего в построении не изменится, кроме того, что a^2 + b^2будет меньше, чем c^2 и функция от угла поменяет знак. □

Для тех, кто хочет «поиграть» с этим построением, есть чертёж в Geogebra. Можно подвигать красную точку C и посмотреть какой будет трапеция для различных треугольников.

Есть, как минимум ещё одно доказательство теоремы косинусов, не опирающееся на теорему Пифагора. Но оно мне нравится меньше, поскольку требует решения системы уравнений.

Располагая уже доказанной теоремой косинусов, можно честно получить теорему Пифагора и без построений, просто, как частный случай, вспомнив, что перпендикулярные векторы ортогональны.

Через теорему синусов

Это «то самое» доказательство Джексон и Джонсон. Иллюстрация и рассуждения были реконструированы автором канала MathTrain, по слайдам, которые девочки показывали на заседании математического общества.

Начнём с того, что достроим прямоугольный треугольник со сторонами a,  b и c (он показан персиковым цветом) до равнобедренного. После чего проведём две вспомогательные линии. Одну, продолжающую гипотенузу зелёного треугольника, а другую — перпендикулярную гипотенузе персикового

Теперь вычислим стороны получившегося длинного прямоугольного треугольника. Девушки сделали это достаточно остроумно: они вписали в треугольник множество копий исходного треугольника, масштабированных отношением катетов r=a/b. Это позволяет вычислить стороны, воспользовавшись суммированием бесконечной убывающей геометрической прогрессии:

\begin{align*}&X = 2cr(1+r^2+r^4+...) = \frac{2cr}{1-r^2}=\frac{2abc}{b^2-a^2},\\&Y = 2c(1+r^2+r^4+...)-c = \frac{2c}{1-r^2}-c=\frac{c(a^2+b^2)}{b^2-a^2}. \end{align*}

Осталось немного. Найдём отношение X к Y, которое равно синусу угла 2\alpha:

\sin(2\alpha)=\frac{X}{Y} = \frac{2ab}{a^2+b^2}.

С другой стороны, используя теорему синусов, легко выразить этот же синус по-другому:

\frac{2a}{\sin(2\alpha)} = \frac{c}{\sin(\beta)}

Из исходного треугольника, согласно определению, \sin(\beta) = b/c. Подставив это отношение, мы приходим к тому, что

\sin(2\alpha) = \frac{2ab}{c^2}.

Приравнивая два решения для \sin(2\alpha), мы и получаем заветное пифагорово соотношение. □

Использование сходящейся геометрической прогрессии не является супероригинальным приёмом. Известно более изящное доказательство, использующее пропорционально уменьшающиеся треугольники.

Интрига была создана вокруг давнего предположения о том, что чисто тригонометричеких доказательств теоремы Пифагора, явно или неявно не опирающихся на тождество \cos^2(x)+\sin^2(x)=1, быть не может.

Надо, однако заметить, что в приведённом доказательстве тригонометрия оказалась ни при чём. Вместо использования теоремы синусов можно было опустить дополнительную высоту в равнобедренном треугольнике и воспользоваться подобием треугольников. А синус тут играет роль формального символа, и никакие его тригонометрические свойства (например, синус двойного угла, периодичность и т.п.) не задействованы. Так что, увы, сенсации не получилось и боюсь, что об этом «историческом» доказательстве будут помнить недолго.

Через тригонометрию

Не смотря на распространённую веру в несуществование тригонометрических доказательств теоремы Пифагора, одно такое доказательство было предъявлено в работе Джейсона Зимбы 2009 года. Этот подход был позже развит Нуно Луизиа, который привёл ещё два способа вывести тригонометрический аналог теоремы Пифагора, опираясь исключительно на алгебраические свойства синуса и косинуса.

В сердце этих доказательств лежит геометрический вывод формулы для косинуса суммы двух углов:

\cos(\alpha+\beta) = \cos(\alpha)\cos(\beta) - \sin(\alpha)\sin(\beta),

Этот вывод базируется на том, что сумма углов в треугольнике равна развëрнутому углу, и на соображениях, сходных с теми, что мы использовали при доказательстве теоремы косинусов. Из выражения для косинуса суммы авторы разными путями приходят к тождеству \cos^2(\alpha)+\sin^2(\alpha) = 1,соответствующему теореме Пифагора в треугольнике с единичной гипотенузой.

Что общего во всех этих доказательствах?

Прямой угол

Теорема Пифагора сформулирована для прямоугольных треугольников. Какое бы доказательство вы ни выбрали, в некоторый момент вам потребуется эта прямоугольность. Но что именно делает особенным прямой угол?

Евклид о прямом угле пишет в самой первой главе первой книги своих знаменитых Начал, и определяет его как »угол, равный своему смежному». Это прекрасное и очень глубокое определение! Можно несколько переформулировать его в главное свойство, которое нам нужно от прямого угла:

Прямой угол — это половина развёрнутого угла.

или так:

Прямой угол — это угол между прямой и любой осью её симметрии.

Отражение этого свойства вы можете найти в доказательствах, использующих построение квадрата из одинаковых прямоугольных треугольников, а также в тех, что опираются на регулярные замощения плоскости. Именно связь прямого угла с симметрией прямой делает его таким особенным!

Кроме того, в первой же книге Евклид приводит доказательство обратное пифагоровому: если в треугольнике квадрат одной стороны равен сумме квадратов других сторон, то он прямоугольный. Получается, что эти два утверждения эквивалентны и не бывает прямоугольных треугольников, для которых не выполняется теорема Пифагора, и нет пифагоровых треугольников, кроме прямоугольных.

Длина

В формулировке теоремы Пифагора также присутствует термин «длина», которая определена, если пространство в котором мы работаем метрическое. Расстояние между точками в пространстве можно определять по‑разному. Можно воспользоваться метриками, использующими координаты, такими, как метрика городских кварталов или метрика Чебышёва. Можно выделить некоторую точку, и определить с её помощью экзотическую французскую железнодорожную метрику. Во всех этих случаях формулировку теоремы Пифагора надо будет существенно корректировать, если не отказаться от неё вовсе.

Но ведь привычная для нас евклидова метрика, при использовании прямоугольных декартовых координат, сама опирается на теорему Пифагора. Нет ли здесь порочного круга: «теорема Пифагора верна в пространстве с евклидовой метрикой, которая, в свою очередь, определяется через теорему Пифагора»? В таком случае, надо ли её вообще доказывать, может быть просто свести её к определению метрики?

От расстояния между двумя точками (длины отрезка) мы ждём того, что оно не будет меняться при параллельных переносах, и произвольных поворотах относительно произвольной точки, а также отражениях относительно произвольных прямых. Эти преобразования называются изометриями и лежат в основе синтетического метода построения евклидовой геометрии. Ни одна из перечисленных выше неевклидовых метрик этим свойством не обладает, как и вообще, никакая метрика, кроме евклидовой. Таким образом, расстояние между точками (длину отрезка) мы определяем как величину, не меняющуюся при изометриях, и уже опираясь на это определение, доказываем теорему Пифагора. После чего, введя ортогональные оси и систему координат, мы можем применить теорему Пифагора для определения расстояния между точками через их координаты.

Понятие расстояния находится в самом сердце евклидовой геометрии. Евклидову метрику можно задать не прибегая к координатам, используя общее понятие вектора и определив скалярное произведение векторов, как билинейную форму, не зависящую от выбора системы координат. Роль длины отрезка, не зависящей от изометрий, будет играть норма вектора, совпадающего с отрезком, которая вычисляется, через результат скалярного произведения вектора на самого себя.

Для, того, чтобы при обсуждении метрического пространства появилась возможность говорить об углах, опять же, потребуется скалярное произведение. Для любого корректно определённого скалярного произведения можно доказать неравенство Коши-Буняковского: |\mathbf{a}\cdot\mathbf{b}| \leq \Vert\mathbf{a}\Vert\Vert\mathbf{b}\Vert,из которого следует, что

-1 \leq \frac{\mathbf{a}\cdot\mathbf{b}}{\Vert\mathbf{a}\Vert\Vert\mathbf{b}\Vert} \leq 1.

Причём, это отношение имеет несколько особых значений:

\frac{\mathbf{a}\cdot\mathbf{b}}{\Vert\mathbf{a}\Vert\Vert\mathbf{b}\Vert} = \begin{cases}1,\quad \text{если}\quad \mathbf{a} = \mathbf{b},\\0,\quad \text{если}\quad \mathbf{a}\cdot\mathbf{b}=0 \\ -1,\quad \text{если}\quad \mathbf{a} = -\mathbf{b},\end{cases}

Если ввести понятие угол между векторами \widehat{\mathbf{a}\mathbf{b}} и некоторую угловую меру для него, то первый случай можно назвать нулевым углом, а третий развёрнутым. Второй случай соответствует ортогональным векторам.

Если ввести некоторую угловую величину, то отношение скалярного произведения двух векторов к произведению их норм можно выразить, как функцию от этой величины и назвать косинусом угла. Конкретные свойства этой функции (кроме перечисленных выше) будут зависеть от выбора угловой величины. Если она будет такой, что между поворотами в пространстве и угловой величиной будет такая связь: R(\varphi)\circ R(\theta) = R(\varphi + \theta),то мы получим родное и привычное понятие геометрического угла и тригонометрического косинуса от него.

\frac{\mathbf{a}\cdot\mathbf{b}}{\Vert\mathbf{a}\Vert\Vert\mathbf{b}\Vert} = \cos(\widehat{\mathbf{a}\mathbf{b}})

В этом случае, угол между ортогональными векторами не будет изменяться при произвольной смене знака любого из векторов, что геометрически соответствует зеркальному отражению. Это означает ортогональные векторы образуют прямой угол. Обратите внимание, на то, что для этих выводов нам не требуется конкретная мера: радианы, градусы или что-то ещё. Достаточно качественных определений: нулевой, прямой и развёрнутый.

Имея скалярное произведение векторов, позволяющее определить метрику, не зависящую от изометрий, к теореме косинусов можно прийти из базового свойства скалярного произведения — линейности. Если рассмотреть два вектора \mathbf{a} и \mathbf{b} и вычислить квадрат длины их разницы, то получим следующее выражение:

\begin{multline*}\Vert\mathbf{a} - \mathbf{b}\Vert^2 = (\mathbf{a}-\mathbf{b})\cdot(\mathbf{a}-\mathbf{b}) = \mathbf{a}\cdot \mathbf{a} + \mathbf{b}\cdot \mathbf{b} - 2\mathbf{a}\cdot \mathbf{b} =\\= \Vert\mathbf{a}\Vert^2 + \Vert\mathbf{b}\Vert^2 - 2\Vert\mathbf{a}\Vert\Vert\mathbf{b}\Vert \cos(\widehat{\mathbf{a}\mathbf{b}})\end{multline*}

Сумма углов в треугольнике.

Одним из свойств угла между векторами является то, что он не меняется при одновременном масштабировании векторов, что позволяет говорить о подобных треугольниках, получающихся друг из друга с помощью преобразования гомотетии. Большая часть доказательств теоремы Пифагора опирается на подобие треугольников, которое позволяет сравнивать между собой отношения сторон и приходить к нужным равенствам. При этом используется следующий критерий подобия:

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.

Этот признак доказывается с помощью построения параллельных прямых и теоремы Фалеса, а также того обстоятельства, что

сумма углов в любом треугольнике равна развёрнутому углу.

Последнее утверждение тоже опирается на существование единственной прямой, параллельной некоторой стороне треугольника, то есть, на пятый постулат Евклида.

Сумма всех углов треугольника равна развëрнутому углу со сторонами, параллельными одной из сторон треугольника.

Сумма всех углов треугольника равна развëрнутому углу со сторонами, параллельными одной из сторон треугольника.

Этот пятый постулат незримо присутствует во всех тысячах доказательств теоремы Пифагора и делает её существенно евклидовой. Если мы перенесёмся на сферу или в геометрию Лобачевского (где хорошо определяются и длины и углы), теорема Пифагора и теорема косинусов в привычном нам виде работать перестанут.

Так что из утверждения «сумма углов в любом треугольнике равна развёрнутому углу» следует теорема косинусов, а также то, что утверждения: «треугольник прямоугольный» и «выполняется теорема Пифагора» эквивалентны.

А можно ли доказать, эквивалентность теоремы косинусов и евклидовости пространства? То есть, верно ли, что если для любого треугольника выполняется теорема косинусов, то сумма углов в нëм равна развёрнутому углу?

Для этого рассмотрим произвольный треугольник ABC и отразим его относительно середины отрезка AB — точки D. Далее, выпишем теорему косинусов для нескольких треугольников

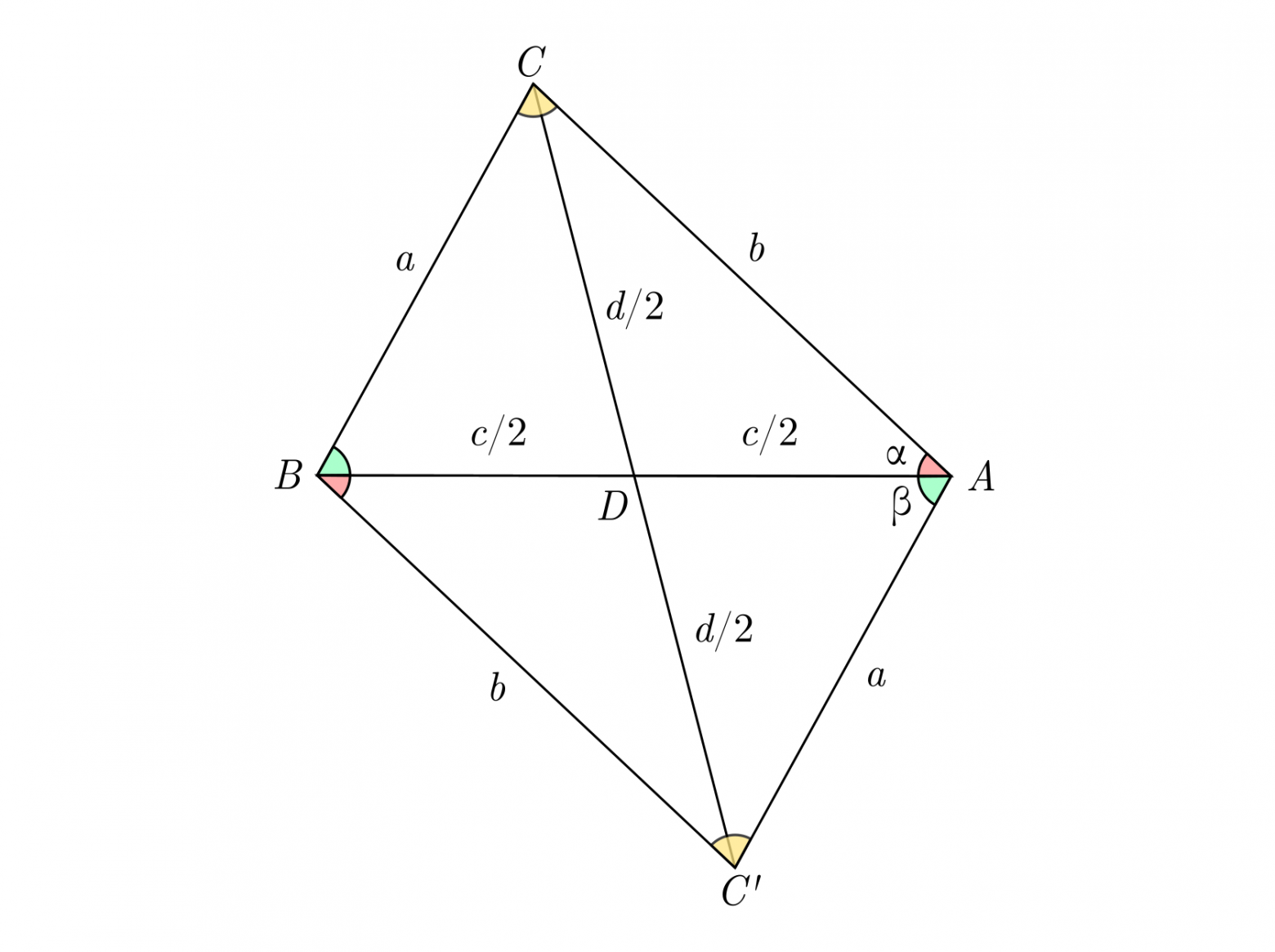
7db7a4786ce67846b99db9f25fa6edc7.png\begin{eqnarray}\triangle ABC&: &c^2 = a^2 + b^2 - 2ab\cos(\gamma)\qquad (1)\\\triangle ABC&:& a^2 = b^2 + c^2 - 2bc\cos(\alpha)\qquad (2)\\\triangle ACC'&:& d^2 = a^2 + b^2 - 2ab\cos(\alpha+\beta)\qquad (3)\\\triangle ADC&:& \frac14d^2 = \frac14c^2 + b^2 - bc\cos(\alpha)\qquad (4)\end{eqnarray}

Выразим величину \cos(α)из (2), величину d^2 — из (4) и подставив их в уравнение (3), получаем:

c^2 = a^2 + b^2 + 2ab\cos(\alpha+\beta).

Используя равенство (1) можно заключить, что \cos(\gamma) = -\cos(\alpha+\beta).

Таким образом, используя только элементарную алгебру и не привлекая каких-либо тригонометрических соотношений, мы получили связь между косинусом суммы двух углов треугольника и косинусом третьего угла в нём. А далее, из базового определения косинуса, легко получить что γ = \pi − α − β,где \pi — это развёрнутый угол. □

Значит, утверждения: «в пространстве выполняется теорема косинусов» (в приведённом выше виде) и «пространство евклидово» эквивалентны.

Для неевклидовых геометрий в пространствах постоянной кривизны: сферической и гиперболической, теорему косинусов нужно переформулировать. Это делается с применением знаний о евклидовой геометрии трёхмерного пространства, в которое вкладываются искривлëнные двумерные подпространства. В этих геометриях и понятие подобия работает не так, как в евклидовом мире, и терема Пифагора перестаёт быть полезной сама по себе.

В завершение рассказа приведу диаграмму, показывающую отношения между теоремами и теориями, которые мы сегодня рассмотрели. Стрелки обозначают отношение «из А следует В».

a7306fdf1faa44a56011044cc292d455.png

© Habrahabr.ru