Машинное обучение от Octave\Matlab к Python
Решил я познакомится с такой интересной для меня областью, как Machine learning. После непродолжительных поисков я обнаружил достаточно популярный курс Стэнфордского университета Machine learning. В нем рассказываются основы и дается широкое представление о machine learning, datamining, and statistical pattern recognition. Был для меня в этом курсе небольшой минус как Python программиста- домашние задания надо было выполнять на Octave\Matlab. В итоге я не пожалел, что получил представления о новом языке программирования, но как учебный пример для более тесного знакомства с соответствующими библиотеками решил переписать домашние задания на Python. То что получилось лежит на GitHub тут.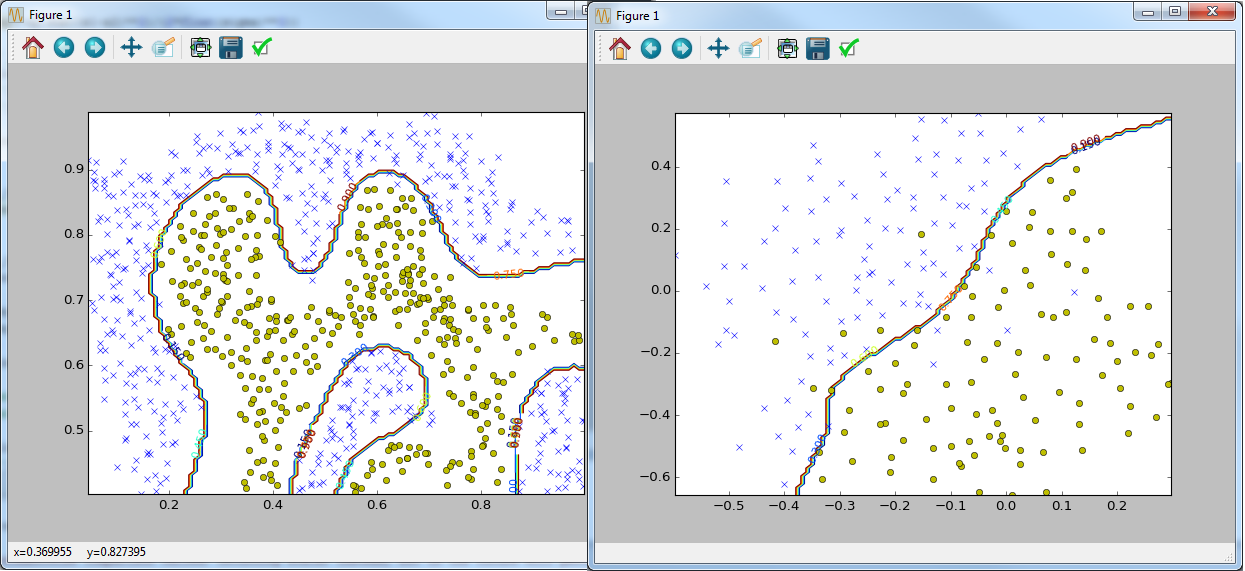
if __name__ == '__main__':
data = sio.loadmat('ex6data1.mat')
y = data['y'].astype(np.float64)
X = data['X']
visualize_boundary_linear(X, y, None)
C = 1
model = svm_train(X, y, C, linear_kernel, 0.001, 20)
visualize_boundary_linear(X, y, model)
C = 100
model = svm_train(X, y, C, linear_kernel, 0.001, 20)
visualize_boundary_linear(X, y, model)
x1 = np.array([1, 2, 1], dtype=np.float64)
x2 = np.array([0, 4, -1], dtype=np.float64)
sigma = 2.0
sim = gaussian_kernel(x1, x2, sigma);
print('Gaussian Kernel between x1 = [1; 2; 1], x2 = [0; 4; -1], sigma = 0.5 : (this value should be about 0.324652)')
print('Actual = {}'.format(sim))
data = sio.loadmat('ex6data2.mat')
y = data['y'].astype(np.float64)
X = data['X']
visualize_data(X, y).show()
C = 1.0
sigma = 0.1
partialGaussianKernel = partial(gaussian_kernel, sigma=sigma)
partialGaussianKernel.__name__ = gaussian_kernel.__name__
model= svm_train(X, y, C, partialGaussianKernel)
visualize_boundary(X, y, model)
data = sio.loadmat('ex6data3.mat')
y = data['y'].astype(np.float64)
X = data['X']
Xval = data['Xval']
yval = data['yval'].astype(np.float64)
visualize_data(X, y).show()
best_C = 0
best_sigma = 0
best_error = len(yval)
best_model = None
for C in [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30]:
for sigma in [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30]:
partialGaussianKernel = partial(gaussian_kernel, sigma=sigma)
partialGaussianKernel.__name__ = gaussian_kernel.__name__
model= svm_train(X, y, C, partialGaussianKernel)
ypred = svm_predict(model, Xval)
error = np.mean(ypred != yval.ravel())
if error < best_error:
best_error = error
best_C = C
best_sigma = sigma
best_model = model
visualize_boundary(X, y, best_model)
Но так как Python есть своя популярная библиотека для этих целей scikit-learn, я попытался переписать некоторые задания с использованием этой возможности (соответствующие файлы с суффиксом sklearn). Как и требовалось ожидать код с библиотекой работает быстрые и выглядит компактнее и понятнее (с моей точки зрения).
if __name__ == '__main__':
data = sio.loadmat('ex6data1.mat')
y = data['y'].astype(np.float64).ravel()
X = data['X']
visualize_boundary(X, y, None)
C = 1
lsvc = LinearSVC(C=C, tol=0.001)
lsvc.fit(X, y)
svc = SVC(C=C, tol=0.001, kernel='linear')
svc.fit(X, y)
visualize_boundary(X, y, {'SVM(linear kernel) C = {}'.format(C): svc,
'LinearSVC C = {}'.format(C): lsvc})
C = 100
lsvc = LinearSVC(C=C, tol=0.001)
lsvc.fit(X, y)
svc = SVC(C=C, tol=0.001, kernel='linear')
svc.fit(X, y)
visualize_boundary(X, y, {'SVM(linear kernel) C = {}'.format(C): svc,
'LinearSVC C = {}'.format(C): lsvc})
data = sio.loadmat('ex6data2.mat')
y = data['y'].astype(np.float64).ravel()
X = data['X']
visualize_boundary(X, y)
C = 1.0
sigma = 0.1
gamma = sigma_to_gamma(sigma)
svc = SVC(C=C, tol=0.001, kernel='rbf', gamma=gamma)
svc.fit(X, y)
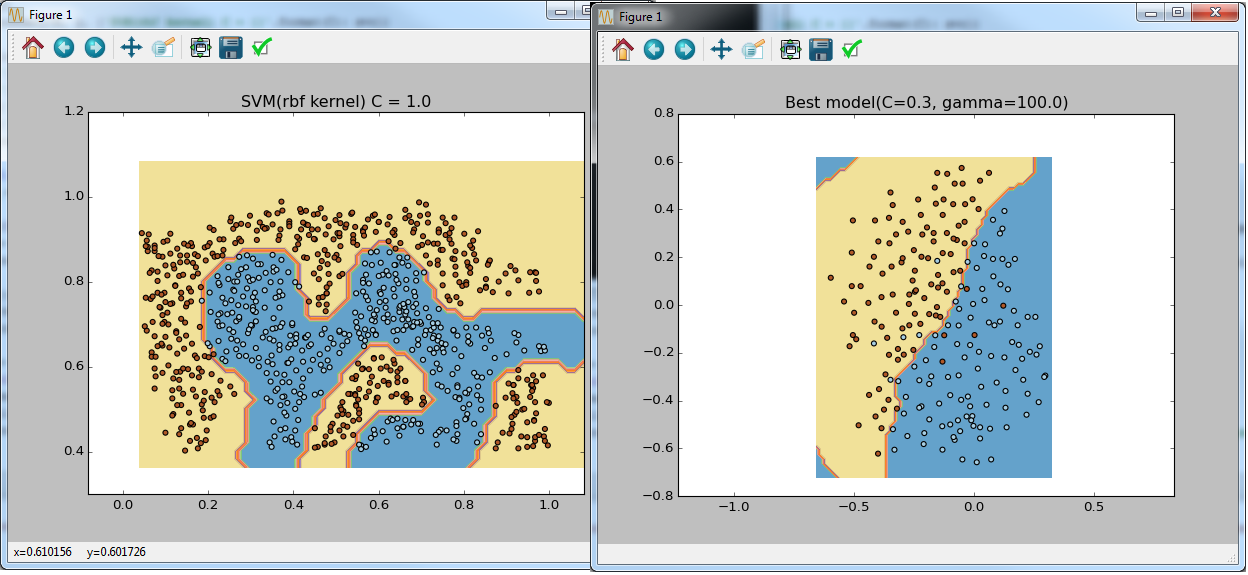
visualize_boundary(X, y, {'SVM(rbf kernel) C = {}'.format(C): svc})
data = sio.loadmat('ex6data3.mat')
y = data['y'].astype(np.float64).ravel()
X = data['X']
Xval = data['Xval']
yval = data['yval'].astype(np.float64).ravel()
visualize_boundary(X, y)
C_coefs = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30]
sigma_coefs = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30]
svcs = (SVC(C=C, gamma=sigma_to_gamma(sigma), tol=0.001, kernel='rbf') for C in C_coefs for sigma in sigma_coefs)
best_model = max(svcs, key=lambda svc: svc.fit(X, y).score(Xval, yval))
visualize_boundary(X, y, {'Best model(C={}, gamma={})'.format(best_model.C, best_model.gamma): best_model})
#Let's do the similar thing but using sklearn feature
X_all = np.vstack((X, Xval))
y_all = np.concatenate((y, yval))
parameters = {'C':C_coefs, 'gamma': map(sigma_to_gamma, sigma_coefs)}
svr = SVC(tol=0.001, kernel='rbf')
clf = GridSearchCV(svr, parameters, cv=2)
clf.fit(X_all, y_all)
visualize_boundary(X, y, {'Best model(C={}, gamma={})'.format(clf.best_params_['C'], clf.best_params_['gamma']): clf})
P.S.
Для тех кому интересна библиотека Sklearn я бы посоветовал:
Курс на udacity
Видео 1 с pycon
Видео 2 с pycon
P.P. S
Для разработки и запуска примеров я использовал дистрибутив Anaconda
