Лазерная локация Луны. Отражение света от наклонного движущегося зеркала
Как известно, и мы, и американцы, установили на Луне уголковые отражатели, благодаря чему с помощью лазера можно измерять расстояние до неё с точностью до уже сантиметров.
Уголковый отражатель отражает падающий от излучателя луч строго в обратном направлении. Но это так, если излучатель и уголковый отражатель взаимно неподвижны. При локации Луны имеем, что Луна движется по орбите радиусом 380000 км со скоростью около 1,3 км/сек, и поверхность земли с излучателем и приёмником тоже движется, если я правильно понял, в ту же сторону со скоростью от 0,46 км/сек на экваторе до в два раза меньшего значения на 60-й широте.
Кроме того, законы отражения от движущегося зеркала отличаются для случаев, если свет волна и если свет частица. Насколько же промахивается отражённый от Луны луч и можно ли это заметить? Вычислим это, причём не выходя за рамки школьной математики. Автор будет благодарен за замечания и указания об ошибках.
Расчёт двойного отражения от движущихся зеркал уголкового отражателя не кажется простой задачей. Например, в статье Б.М. Болотовского и С.Н. Столярова »Отражение света от движущегося зеркала и родственные задачи» рассматривается только отражение от зеркала движущегося перпендикулярно своей поверхности путём пересчёта характеристик электромагнитных полей выражаемых уравнениями Максвелла. При этом обоснование метода излагается на 14 страницах.
Попробуем решить задачу для движущегося наклонного зеркала анализируя движение фронтов падающей и отражённой волн. Рассмотрим участок AO фронта волны шириной S. Луч (синие линии со стрелками) падает на зеркало (голубая линия) под углом φ от вектора скорости его движения V. Отражается он под углом ψ (зелёная дуга). Угол наклона нормали зеркала к вектору скорости равен α. Это конечно не полная 3D-схема, но для уголкового отражателя сгодится.
После попадания в зеркало края фронта AO волны в точке O, другой его край продолжает движение пока не попадёт в зеркало в точке C. На это потребуется время t и лучи, падающий и отражённый, пройдут расстояние c∙t, где с — скорость света. Следовательно, BO = AC. Это значит, что прямоугольные треугольники OAC, ODC и OBC равны.
Зеркало за это время сдвинется на расстояние V∙t, и часть расстояния до точки C добавится из-за наклона зеркала на угол α.
Рис. 1
Перейдём к световым единицам измерений. Положим св.ед.скорости = ед.скорости/ скорость света и тогда V→β. Мы знаем, что движущееся зеркало сокращается пропорционально коэффициенту Лоренца. Следовательно, угол α связан с углом α0 наклона зеркала в его собственной системе отсчёта формулой (1). На схеме рис. 1 расстояние AC выражается формулой (2). Из (2) и (3) вычислим c∙t и y, и подставим в уравнение (4), откуда найдём значение x по формуле (6) и далее c∙t из (2). Затем вычислим tg δ по формуле (7). Из чертежа следует, что углы падения φ и отражения ψ связаны соотношением (8), которое и является решением задачи.
Уравнение (9) получено из мысленного эксперимента, заключающегося в том, что позиции источника света, зеркала и отражённого «зайчика» на экране, зафиксированные на лабораторном столе при его неподвижности, не должны измениться, когда он начнёт двигаться. Это следует из принципа относительности. Значения, вычисленные по формулам (8), удовлетворяют уравнению (9) при всех разумных сочетаниях углов падения, наклона зеркала и скорости. Естественно, при нулевом наклоне зеркала результаты совпадают с расчетами по формулам Болотовского и Столярова.
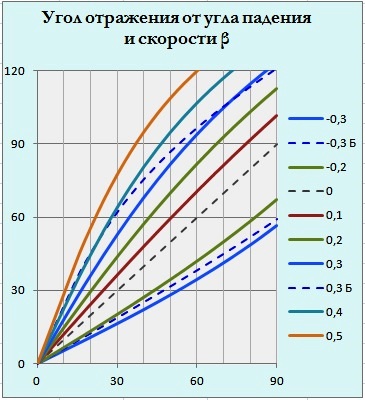Для расчёта отклонения отражённого луча от исходного направления можно воспользоваться формулой углов отражения при нулевом наклоне зеркала. Дело в том, что если сверху к вертикальному зеркалу приставить горизонтальное, то мы получим уголковый отражатель при его предельном угле поворота. Результаты показаны на рис. 2. Прямые расчёты математической модели движущегося уголкового отражателя по формуле (8) показали независимость угла отклонения отражённого луча от поворота отражателя.
Графики приведены для диапазона скоростей зеркала от встречного движения -0,3 световой до +0,5 вдогонку.
Рис. 2
Кстати, при отражении луча догоняющего зеркало, угол отражения может превышать 90°, как это отображено на рис. 1. Для сравнения приведены графики отклонения для баллистической теории света отображённые синими пунктирными линиями для скоростей -0,3 и +0,3 световой и отмеченных литерой «Б». В этой теории свет считается частицами, а теория относительности отвергается. Расчёт проводился согласно школьной методике. Как видим, отклонения в таком случае будут иные, так что прямой эксперимент мог бы подтвердить или отвергнуть баллистическую теорию.
Итак, насколько же «зайчик» от уголкового отражателя на Луне отклонится от места установки лазера на Земле? Расчёты показывают, что максимальный угол отклонения, в точке верхней кульминации Луны, будет 0,0005 градуса. На Земле отклонение составит примерно 3,3 км в сторону движения Луны по орбите, но за 2,5 секунды, пока импульс возвратится, земная поверхность подъедет почти на километр, так что итоговое отклонение составит около 2,5 км. Поскольку размер отражённого лазерного зайчика на земной поверхности составляет порядка 15 км, заметить сам факт отклонения пока невозможно. И, кстати, отклонение по баллистической теории для этих условий совпадает с отклонением по СТО до 8-го знака (т.е. расхождение не более 10 метров).
