LASSO и Ridge Регрессия. Что же значит та картинка
Пыталась я вникнуть в устройство регрессии LASSO и Ridge… И сделала объективный вывод, что верхнеуровнево про них много где хорошо и подробно написано. Человеку непосвящённому легко найти понятные объяснения, просто погуглив. Но я-то человек посвящённый! Я хочу понять! Но вот беда — в русскоязычных блогах я нигде не смогла найти толкового прояснения некоторых метаматематических моментов работы лассо и ридж регрессии. Пришлось доходить до понимания самой с опорой на пару англоязычных источников, и я решила изложить некоторую математику, лежащую в основе лассо и ридж в этой статье.
И снова про регрессию (полиномиальную)
Начнём с основных определений. Представим, что у нас есть наблюдения, которые характеризует один признак. Например, мы хотим предсказать количество предстоящих лет жизни человеку по его индексу массы тела — такое вот у нас исследование. У нас есть набор данных «с ответами» — то есть табличка соответствия «ИМТ в 30 лет → n оставшихся лет» собранная с населения какой-нибудь скандинавской страны.
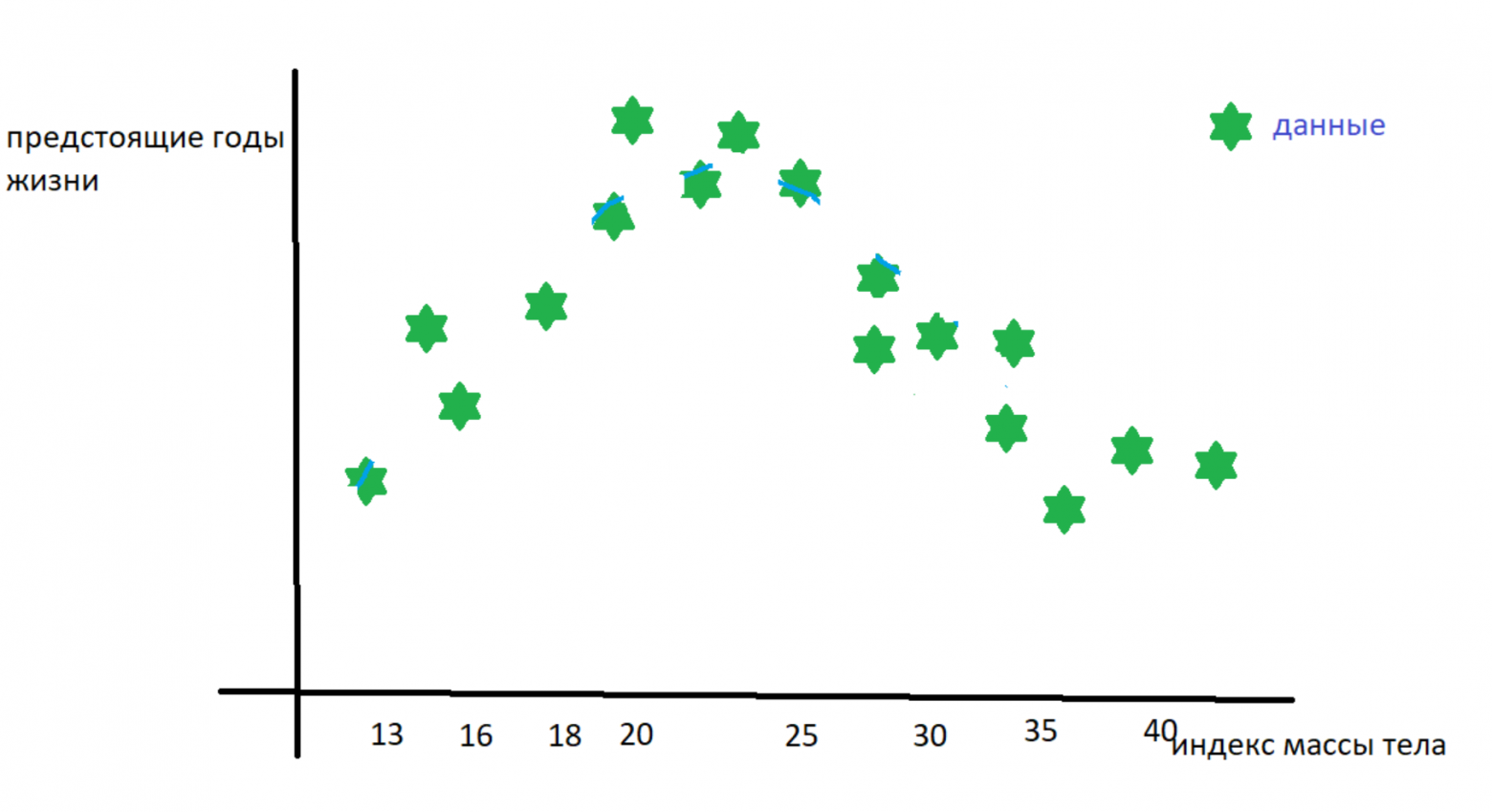данные взяты с потолка
Дальше всякими правдами и не-правдами догадываемся, что зависимость годов жизни от ИМТ описывается полиномом степени 2, а значит надо искать три коэффициента — при 
, 
и при 
(он же сдвиг кривой по оси ординат).
Чтоб найти коэффициенты, возьмём наш набор наблюдений-иксов и «раскроем его» — вместо одного икса сделаем икс в нулевой, икс в первой (он же просто икс) и икс в квадрате, — чтоб найти уместные коэффициенты перед каждым компонентом уравнения полиномиальной регрессии.
превращаем икс в три степени икса
Решим матричное уравнение. В матрице у нас каждый ряд представляет собой одно наблюдение, в нашем случае — одного человечка. Вектор w — искомый вектор коэффициентов регрессии. Вектор игрек — вектор количества лет — одно число для каждого человечка. Хорошо про решение таких уравнений для поиска коэффициентов регрессии написано тут.
Решаем и получаем что-то типа 
— искомый полином степени 2.
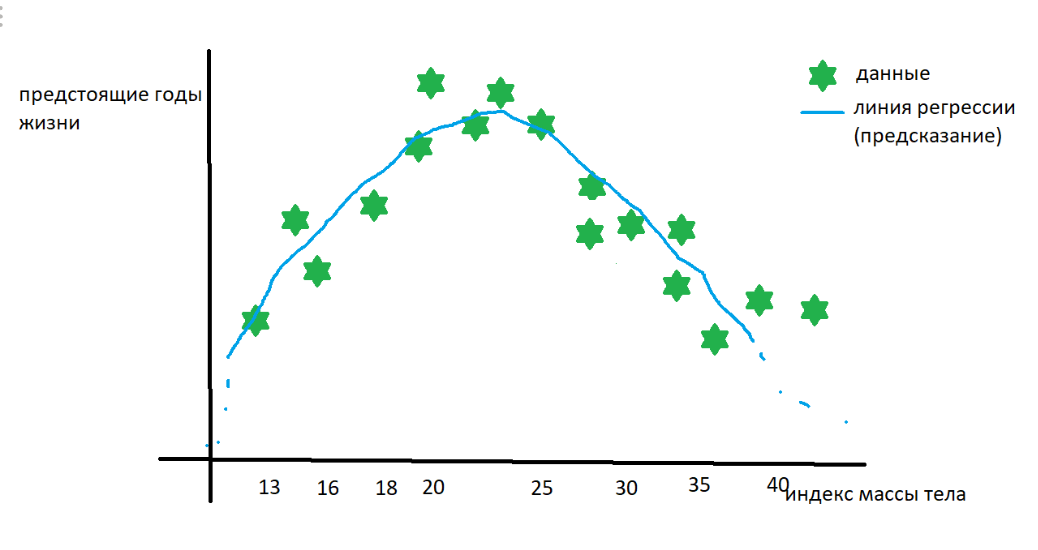предположения о зависимости ИМП и лет жизни тоже взяты с потолка
Bam! Мы построили линию регрессии и теперь по ИМТ можем предсказывать дату смерти!
И снова про проклятие размерности
На самом деле и в жизни, и в науке исследователи далеко не всегда знают, какие признаки влияют на целевую переменную. Влияет ли на доходность бизнеса средняя продолжительность рабочего дня CEO компании? А широта и долгота главного офиса компании? Влияет ли на дату смерти человека аномалии в гене OCA2 (один из генов, кодирующих цвет радужки)?
Часто исследователи стараются зафиксировать как можно больше признаков — порода домашнего животного, ИМТ, уровень глюкозы, рост — просто на всякий случай. Но если мы будем учитывать все собранные признаки, то существует риск большой дисперсии модели на новых данных. Конечно, если у нас для одного человека собрано 100 фич, среди которых ИМТ, цвет глаз, порода собаки, количество морганий в минуту, то модели будет сложно выделить действительно значимые тренды и при изменении одного, даже самого незначительно признака (например, количество морганий изменили на +2) предсказание — оставшиеся года жизни — изменится радикально. И вот уже человеку жить не 50 лет, а 30. А ещё может быть такой случай — признаки, которые мы собрали, сильно скоррелированы. Например, вес человека утром и вес человека перед сном. Скоррелированные признаки сильно мешают нам в решении матричного уравнения, так как становится трудно построить обратную матрицы. Подробнее про такие плохо обусловленные задачи написано тут.
Представим, что мы собрали чуть больше данных о наших скандинавских ребятах. Теперь у нас есть не только их ИМТ, но ещё количество морганий в час. Теперь признаковое пространство стало двумерным. Координата точки по икс1 и икс2 — в нижней полуплоскости — даёт нам представление о том, какой у человека ИМТ и сколько раз в час он в среднем моргает. Красная парящая точка в воздухе — есть предсказание оставшиеся лет.
Попробуем развернуть это трёхмерное пространство — разбить его на два двумерных и посмотреть на зависимость целевой переменной от каждого признака.
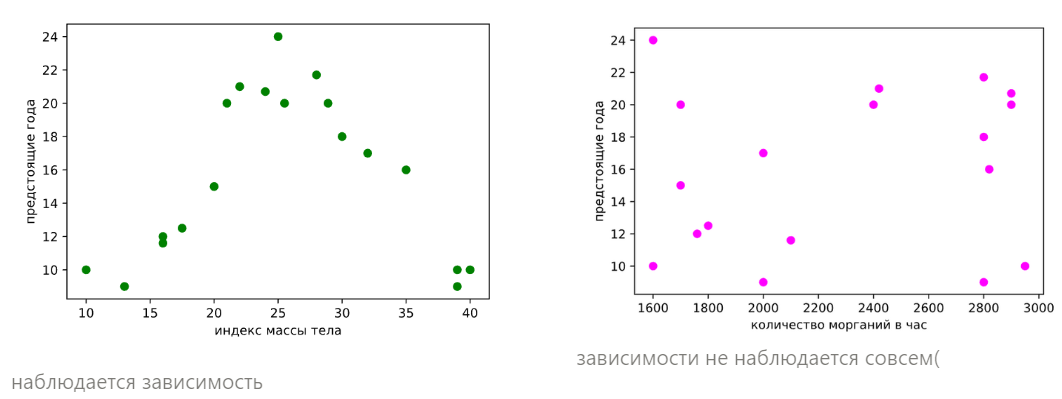
Итак, теперь нам очевидно, что зависимости между количество морганий в час и годами нет. Даже на глаз, не говоря уже о логике. Но что, если у нас миллион таких признаков и 10 миллионов наблюдений? Не смотреть же миллион графиков. Да и зависимости могут быть хитрее. В общем, хотелось бы какое-нибудь изящное математическое решение проблемы, чтоб математика сама признаки, которые не вносят вклад в предсказание, убирала. А ещё чтоб избавлялась от скоррелированных признаков. К примеру, если б мы решили о наших скандинавах собирать вес в килограммах и индекс массы тела, хотелось бы, чтобы модель нам деликатно один из этих высоко-скорелированных признаков убрала. Где же такая волшебная машина?
И снова про регуляризацию
В общем, стало быть, в задаче со ста фичами, когда мы предполагаем, что значимыми являются ну максимум 20, нам надо как-то эти 20 определить. Тут на помощь приходит регуляризация.
