Квантовое программирование для диспетчеризации производства15.11.2023 10:45

Лучший способ изучить новую технологию это применить ее на практике. Но как быть, если у вас нет квантового компьютера, а на изучение физики нет времени/желания? Это не проблема, потому что сегодня мы разберем наиболее доступный и безболезненный способ погружения в квантовые алгоритмы на примере комбинаторной оптимизации. И начнем с распространенной задачи, которая возникает на производстве — диспетчеризация технологических операций. Устраивайтесь поудобнее, приготовьте чашку любимого напитка и поехали!

Введение

В мире квантовых вычислений существует множество конкурирующих парадигм и подходов, включая адиабатический, универсальный, на основе сверхпроводящих схем, фотонных и других аппаратных реализациях. Различия обусловлены как элементной базой, так и перечнем доступных квантовых операций. Мы не будем вдаваться в них детально, а рассмотрим наиболее доступную на сегодняшний день парадигму квантовых вычислений — адиабатическую.

Адиабатическая модель

Для начала опишем суть рассматриваемой модели. В качестве аналогии приведем полносвязный граф, вершины которого могут находиться в одном из 2-х дискретных состояний — 0 или 1. Энергия графа определяется как сумма весов всех ребер, обе соседние вершины которых находятся в состоянии 1. Помимо весов ребер, у каждой вершины также есть вес и он добавляется к суммарной энергии графа, если вершина находится в состоянии 1.

Аппаратно данный граф реализуется с помощью т.н. спиновых стекол (spin glass) в форме 2-мерных решеток, над которыми осуществляется адиабатическая эволюция. Не погружаясь в физику процесса достаточно сказать, что в результате эволюции система переходит в минимальное энергетическое состояние, т.е. частицы принимают состояния, при которых энергия графа минимальна.

Стоит отметить, что аппаратная реализация основана на базисе +1 / -1 (также известна как модель Изинга), вместо 0/1, но оба представления являются взаимо-трансформируемыми и не меняют сути процесса.

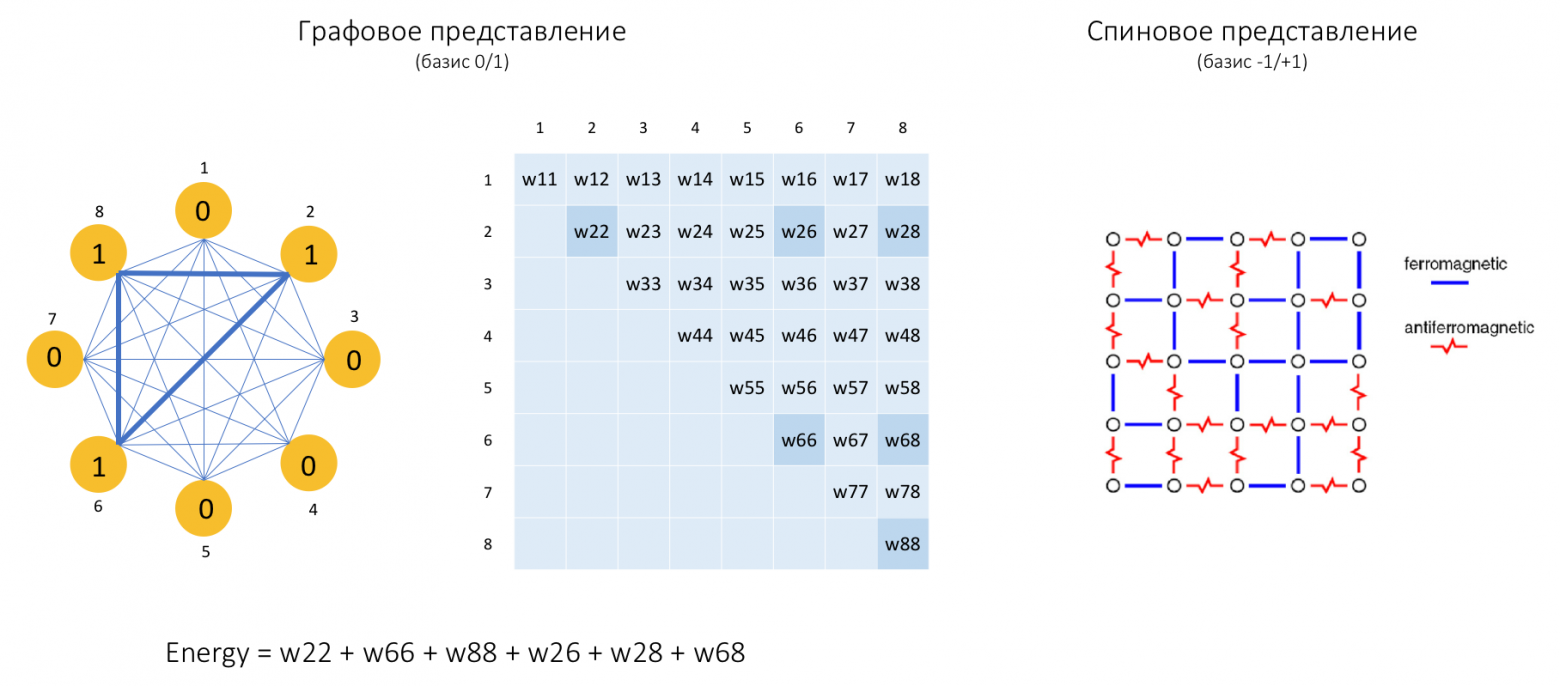
Адиабатическая модель(графовое и спиновое представление)

Адиабатическая модель
(графовое и спиновое представление)

Описанную выше постановку можно сформулировать математически в следующем виде:

\underset{x}{\mathrm{argmin}}(x^T\cdot Q \cdot x) \\ x = (x_1, x_2, ..., x_n), x_i \in (0,1)

В терминах теории оптимизации такая задача называется квадратичная дискретная оптимизация без ограничений (в англ. QUBO) и несмотря на внешнюю тривиальность обладает несколькими важными особенностями:

  • Данная задача относится к классу NP-сложных. Т.е. для любых размерностей выше 25–100 поиск точного решения становится непосильным даже для классических компьютеров,

  • Любую известную NP-сложную задачу можно свести к данной постановке,

  • Постановка совместима как с квантовым, так и классическим компьютерами.

Поскольку рассматриваемая нами задача о расписаниях тоже относится к классу NP-сложных, то нам потребуется только написать алгоритм трансформации, остальное — выполнит квантовый компьютер (или классический). Но перед тем, как приступить к трансформации следует до-определить входную задачу.

Постановка задачи

Задача о расписаниях имеет множество различных вариаций в зависимости от количества станков, операций, критичности сроков, наличие штрафов за их нарушение и других особенностей. Для простоты понимания мы рассмотрим постановку с одним станком, несколькими задачами и жесткими сроками их выполнения. Если срок выполнения задачи соблюдается, то исполнитель получает определенную компенсацию, и не получает если срок нарушается.

Обобщим входные условия:

(1) Дано n задач и 1 станок,
(2) Для каждой задачи известно:
— Время выполнения (ti),
— Срок выполнения (di),
— Премия (pi).
(3) Если задача выполнена в срок (т.е. tstarti + ti <= di), то назначается премия pi,
(4) Задачи выполняются строго последовательно,
(5) Задачи можно выполнять в любой последовательности.

Необходимо:

(6) Определить последовательность выполнения задач (tstart1, tstart2, …, tstartn) таким образом, чтобы максимизировать суммарную премию P = sum (pi), для всех i для которых выполняется условие tstarti + ti <= di.

Все дальнейшие иллюстрации будут приведены для следующих входных данных: 

# Время выполнения задач
times = [2, 2, 1, 1]
# Сроки
deadlines = [3, 4, 4, 3]
# Премии
profits = [23, 20, 37, 36]

Общий подход

Для решения задачи необходимо сформулировать преобразование входных условий задачи в квадратичную форму матрицы Q таким образом, чтобы функционал xT * Q * x достигал своего минимума только в том случае, когда выполнялось условие максимизации суммарной премии P.

Введем индекс ki, t, соответствующий i-ой задачи, запущенной в t-ый момент времени:

k_{i,t} = i \cdot T_{max} + t

Тогда значения элементов вектора x обозначим как:

x_{k_{i,t}} = \begin{cases} 1 & \text{если $i$-я задача запущена в $t$-ый момент времени}\\ 0 & \text{иначе} \end{cases}

Теперь определим функционал Q как сумму штрафов и премий:

(а) Штрафная добавка за повторный запуск задачи:

Q[k_{i,t_1}, k_{i,t_2}] = P_1, \\ t_2 \neq t_1

(б) Штрафная добавка за нарушение условия последовательного выполнения задач:

Q[k_{i,t_1},k_{j,t_2}] = P_3 \\ t_1 \leq t_2 \leq t_1 + t_i

(в) Премия за выполнение задачи раньше крайнего срока:

Q[k_{i,t},k_{i,t}] = -p_i\\ t + t_i\leq d_i

Обратите внимание, что премия принимает отрицательное значение. Это необходимо, поскольку мы решаем задачу минимизации функционала.

Итоговая матрица Q имеет следующий вид (на примере частной задачи):

Форма матрицы Q

Форма матрицы Q

Программирование и отладка

Теперь мы можем переложить сформулированную трансформацию в код.

Введем вспомогательные функции кодировки и декодировки индексов.

def decode_index(i, max_time):
  job_id = i // max_time
  start_time = i - job_id * max_time
  return job_id, start_time

def encode_index(job_id, start_time, max_time):
  return job_id * max_time + start_time

И сформируем матрицу QUBO: 

def make_qubo(times, deadlines, profits):
  max_time = np.max(deadlines)
  num_jobs = len(times)

  size = max_time * num_jobs
  Q = np.zeros((size, size))

  P = 1000
  for job_id in range(num_jobs):
    for start_time in range(max_time):
      time = times[job_id]
      deadline = deadlines[job_id]
      i = encode_index(job_id, start_time, max_time)

      # Apply profit, if completed before deadline
      if start_time + time <= deadline: Q[i, i] = -1.0 * profits[job_id]

      # Should start each job only once
      # Otherwise, apply penalty P
      for t in range(max_time):
        if start_time != t:
          j = encode_index(job_id, t, max_time)
          Q[i][j] = P
          Q[j][i] = P

      # Should start one job after another
      # Otherwise, apply penalty P
      for job_id_2 in range(num_jobs):
        if job_id_2 != job_id:
          time = times[job_id]
          for t in range(start_time, min(start_time + time, max_time)):
            j = encode_index(job_id_2, t, max_time)
            Q[i][j] = P
            Q[j][i] = P
  return Q

Трансформация готова, теперь можно преобразовать входную задачу в матрицу Q, найти минимум и получить оптимальное расписание задач. Как мы уже писали, поиск минимума функционала QUBO можно осуществлять не только на квантовом компьютере (о нем позже), но также с помощью прямого перебора (brute-force) и путем линеаризации задачи с последующим использованием любого линейного солвера.

Метод прямого перебора ограничен взрывным ростом размерности, поэтому расчет матриц размером больше 25×25 будет довольно затруднителен. Применение линеаризации позволяет искать точный минимум для размерностей до 100×100, а также субоптимальных решений на более высоких размерностях.

Поскольку размерность матрицы Q зависит линейно от произведения n * T_max, где n — количество задач, а T_max — максимальный крайний срок, то наша матрица примет размерность 16×16, что позволит решить задачу любым из упомянутых методов.

Ниже приведен пример для прямого перебора: 

def solve_qubo(Q):
    min_vec = [0] * len(Q)
    min_energy = min_vec @ Q @ min_vec
    for i in range(2**len(Q)):
      x = list(map(int,('{0:0%db}'%(len(Q))).format(i)))
      e = np.dot(x, np.dot(Q, x))
      if e < min_energy:
        min_energy = e
        min_vec = x
    print(min_vec)
    return min_vec, min_energy

Проверим визуальное решение нашей задачи. Видим, что наш солвер отобрал задачи 0, 2 и 3 (задача 1 не отображена на графике, т.к. не входит в оптимальное решение). Такая комбинация дает максимальную премию 23 + 37 + 36 = 96. Если бы солвер попытался выполнить и 1-ю задачу вовремя (со сроком выполнения 4), то произошло бы нарушение сроков у одной из остальных задач и суммарная премия стала бы меньше.

На данном примере видно, что солвер правильно выбирает последовательности задач, исходя из максимизации целевой функции. Используя приведенный код, вы можете провести эксперименты на более сложных комбинациях задач.

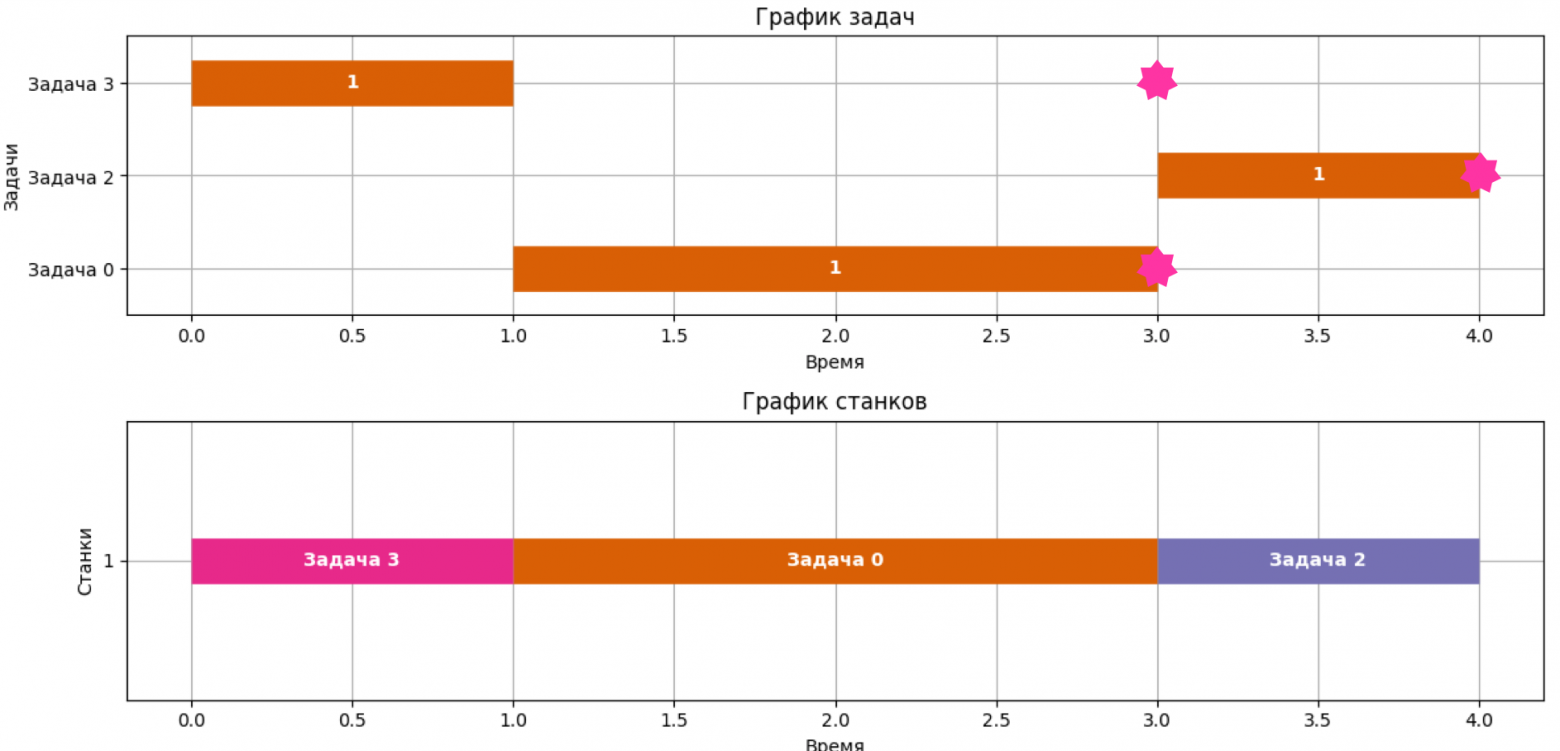
Итоговое расписание

Итоговое расписание

Тестирование на квантовом бэкенде

Настало время поговорить о квантовом компьютере. На данный момент квантовые чипы, реализующие адиабатическую модель вычислений демонстрируют наиболее оптимистическую динамику с точки зрения масштабирования. Крупнейший (и предположительно единственный) вендор в этой области это канадская компания D-Wave, которая регулярно рапортует об удвоении кубитности своих вычислителей (почти в ногу с законом Мура), отгружает свои компьютеры в промышленных масштабах в крупные американские и европейские исследовательские центры.

Для исследователей из ограниченного перечня стран на некоммерческой основе предоставляется облачный доступ к вычислительным ресурсам D-Wave Leap. Если зарегистрироваться на их портале (к сожалению, регистрация из РФ недоступна), то можно получить тестовый доступ в объеме 1-ой минуты в месяц. Ниже мы приведем пример доступа к бэкенду D-Wave и решение описанной нами задачи.

from dwave.system.samplers import DWaveSampler
from dwave.system.composites import EmbeddingComposite

def solve_qubo(Q, API_KEY):
    q = {}
    size = len(Q)
    for i in range(size):
        for j in range(size):
            q[(i,j)] = Q[i][j]
            
    sampler = EmbeddingComposite(DWaveSampler(token=API_KEY]))
    response = sampler.sample_qubo(q, num_reads=200)

    min_energy = np.inf
    min_spins = None
    for sample, energy in response.data(['sample', 'energy']): 
        if energy < min_energy:
          min_spins = sample
          min_energy = energy
    
    return [min_spins[i] for i in range(len(min_spins))], min_energy

Полный код проекта доступен по ссылке на GitHub: quantum-job-scheduler.

Заключение

В данной статье мы осветили наиболее доступный и понятный способ взаимодействия с квантовым компьютером и рассмотрели решение задачи, приближенной к реальному применению. Наша цель была заинтересовать тех, кто еще не знаком с квантовыми вычислениями и помочь в преодолении порога входа в новую и увлекательную область программирования.

Мы также готовы помогать перспективным технологическим компаниям в изучении возможностей квантовых технологий для индустриальных задач. Поэтому если у вас есть задачи, решение которых имеет практическую значимость, напишите о них в комментариях или сообщениях и мы постараемся разобрать их в будущих статьях!

Всем хорошей недели и больших квантовых прорывов!

© Habrahabr.ru