Криптоанализ «Энигмы»

All specialists unanimously agreed that a reading [of the Enigma] is impossible.
Admiral Kurt Fricke, Chief of Naval War Command
Энигма — роторная шифровальная машина, использовавшаяся нацистской Германией в годы Второй мировой войны. Благодаря влиянию, оказанному на ход войны, взлом Энигмы стал возможно самым ярким моментом в многовековой истории криптоанализа. В этом топике я бы хотел рассказать о методе взлома, использовавшимся в Блетчли-парк, а так же описать устройство самой машины.
Роторные машины
Впервые шифровальные роторные машины начали использоваться в начале 20 века. Основным компонентом таких устройств является диск (он же ротор) с 26 электрическими контактами на обоих сторонах диска. Каждый контакт соответствовал букве английского алфавита. Соединение контактов левой и правой сторон реализовывало шифр простой замены. При вращении диска контакты смещались, изменяя тем самым подстановку для каждой буквы. Один диск обеспечивал 26 различных подстановок. Это означает, что при шифровании одного и того же символа, получаемая в результате последовательность начинает повторяться через 26 шагов.
Для увеличения периода последовательности можно использовать несколько роторов, соединенных последовательно. При совершении полного оборота одного из дисков, следующий диск сдвигается на одну позицию. Это увеличивает длину последовательности до 26n, где n — количество соединенных последовательно роторов.
В качестве примера рассмотрим следующее изображение упрощенной роторной машины:
Приведенная машина состоит из клавиатуры (для ввода символа), трех дисков, индикатора (для отображения криптотекста) и реализует шифрование 4 символов: A, B, C, D. В начальной позиции первый диск реализует подстановку: A-C; B-A; C-B; D-D. Подстановки второго и третьего дисков равны A-B; B-C; C-A; D-D и A-A; B-C; C-B; D-D соответственно.
При нажатии буквы B на клавиатуре замыкается электрическая цепь, зависящая от текущего положения роторов, и на индикаторе загорается лампочка. В приведенном выше примере буква B будет зашифрована в C. После чего первый ротор сдвинется на одну позицию и настройки машины приобретут следующий вид:
Энигма
Энигма является наиболее популярным представителем мира шифровальных роторных машин. Она использовалась германскими войсками во время второй мировой войны и считалась практически не взламываемой.
Процедура шифрования Энигмы реализована как в приведенном выше примере за исключением некоторых дополнительных штрихов.
Во-первых, число роторов в разных версиях Энигмы могло отличаться. Наиболее распространенной была Энигма с тремя роторами, но использовался так же вариант с четырьмя дисками.
Во-вторых, процесс расшифровки демонстрационной роторной машины, описанной выше, отличается от процесса шифрования. Каждый раз для расшифровки придется менять левый и правый ротор местами, что может быть не совсем удобным. Для решения этой проблемы в Энигме был добавлен еще один диск, который назывался рефлектор. В рефлекторе все контакты были соединены попарно, реализуя тем самым повторное прохождение сигнала через роторы, но уже по другому маршруту. В отличие от остальных роторов рефлектор всегда находился в фиксированном положении и не вращался.
Добавим рефлектор, реализующий замену (A-B; C-D) к нашей демонстрационной шифровальной машине. При нажатии на клавишу B сигнал проходит через роторы и поступает в рефлектор через контакт C. Здесь сигнал «отражается» и возвращается обратно, проходя через роторы в обратном порядке и по другому пути. В результате чего буква B на выходе преобразуется в D.
Обратите внимание, что если нажать клавишу D, то сигнал пойдет по той же самой цепи, преобразовывая D в B. Таким образом наличие рефлектора делало процессы шифрования и дешифрования идентичными.
Еще одно свойство свойство Энигмы, связанное с рефлектором, заключается в невозможности шифрования какой-либо буквы в саму себя. Это свойство сыграло очень важную роль при взломе Энигмы.
Получившееся устройство уже очень похоже на настоящую Энигму. С одной незначительной оговоркой. Стойкость подобной машины упирается в секретность внутренней коммутации роторов. Если устройство роторов будет раскрыто, то взлом сводится к подбору их начальных позиций.
Так как каждый ротор может находится в одной из 26 позиций, для трех роторов получаем 263=17476 вариантов. При этом сами роторы тоже могут располагаться в произвольном порядке, что увеличивает сложность в 3! раз. Т.е. пространство ключей такой машины составит 6*17576=105456. Этого явно не достаточно для того, чтобы обеспечить высокий уровень безопасности. Поэтому Энигма было оснащена еще одним дополнительным инструментом: коммутационной панелью. Соединяя на коммутационной панели буквы попарно можно было добавить еще один дополнительный шаг к шифрованию.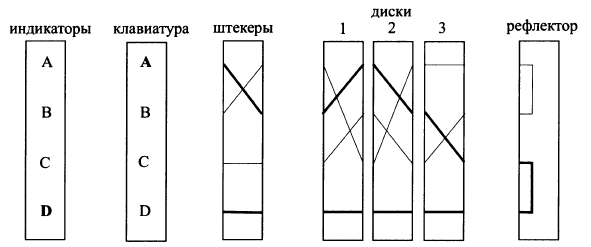
К примеру, предположим что на коммутационной панели буква B соединена с буквой A. Теперь при нажатии на A сперва происходит подстановка A-B, и на вход первого ротора подается буква B.
Аналогичным образом происходит расшифровка сообщения. При нажатии клавиши D роторы и рефлектор производят преобразование D-D-D-D-C-B-A-B. После чего коммутационная панель преобразует B в A.
Анализ стойкости Энигмы
Реальная Энигма отличалась от описанной демонстрационной машиной только в одном. А именно в устройстве роторов. В нашем примере ротор изменяет свое положение только при совершении полного оборота предыдущим диском. В настоящей Энигме каждый диск имел специальную выемку, которая в определенной позиции подцепляла следующий ротор и сдвигала его на одну позицию.
Расположение выемки для каждого из роторов можно было регулировать с помощью специальных внешних колец. Начальное положение колец не влияло на коммутацию роторов и на результат шифрования отдельно взятой буквы, поэтому кольца не учитываются при расчете пространства ключей Энигмы.
Итак, базовая модель Энигмы имела 3 различных ротора, пронумерованных римскими цифрами I, II, III и реализующих следующие подстановки:
Entry = ABCDEFGHIJKLMNOPQRSTUVWXYZ
I = EKMFLGDQVZNTOWYHXUSPAIBRCJ
II = AJDKSIRUXBLHWTMCQGZNPYFVOE
III = BDFHJLCPRTXVZNYEIWGAKMUSQO
При шифровании роторы можно было располагать в любой последовательности, что для трех роторов дает 6 разных комбинаций.
Помимо этого каждый ротор мог быть установлен в одной из 26 возможных стартовых позиций. Т.е. начальное положение роторов имеет всего
6*253=105456 комбинаций.
Количество всех возможных соединений на коммутационной панели вычисляется по формуле n! /((n-2m)! m! 2m), где n — количество букв алфавита, m — количество соединенных пар.
Для 26 буква английского алфавита и 10 пар это составляет 150738274937250=247 различных комбинаций.
Таким образом базовая версия Энигмы с тремя роторами имела солидное даже по современным меркам пространство ключей:
150738274937250*105456=15,896,255,521,782,636,000≈264.
Такое огромное число вариантов внушало обманчивое чувство неуязвимости.
Криптоанализ Энигмы
Большое пространство ключей обеспечивает шифру Энигмы достаточно серьезный уровень стойкости к атакам по известному шифртексту.
Полный перебор 264 вариантов даже на современных компьютерах дело не простое.
Однако все меняется если применить атаку с известным открытым текстом. Для такого случая существует весьма хитроумный метод, позволяющих пренебречь настройками коммутационной панели в процессе поиска ключевой комбинации, что сводит пространство ключей Энигмы всего к 105456 комбинациям и делает весь шифр фатально уязвимым.
Метод эксплуатирует наличие в паре открытый-закрытый текст так называемых «циклов». Чтобы объяснить понятие «цикл», рассмотрим следующее открытое сообщение P и соответствующий ему криптотекст C, зашифрованный Энигмой.
P = WETTERVORHERSAGEBISKAYA
C = RWIVTYRESXBFOGKUHQBAISE
Запишем каждый символ из пары в виде таблицы:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| w | e | t | t | e | r | v | o | r | h | e | r | s | a | g | e | b | i | s | k | a | y | a |
| r | w | i | v | t | y | r | e | s | x | b | f | o | g | k | u | h | q | b | a | i | s | e |
Обратите внимание на подстановки, реализуемые энигмой в 14, 15 и 20 позициях. На 14 шаге буква A шифруется в G. Последняя, в свою очередь, шифруется в K на 15 шаге. И затем буква K зашифровывается в A на 20 шаге, закольцовывая тем самым цепочку A-G-K-A. Такие закольцованные цепочки называются циклами. Наличие циклов позволяет разделить задачу взлома Энигмы на две простые составные части: 1) поиск стартового положения роторов и 2) поиск соединений коммутационной панели при известных установках роторов.
Мы знаем, что при шифровании в Энигме происходит несколько преобразований. Сперва сигнал проходит через коммутационную панель. Результат преобразования на коммутационной панели поступает в роторы. После чего сигнал попадает на рефлектор и возвращается через роторы на коммутационную панель, где выполняется последняя подстановка. Все эти операции можно представить математической формулой:
Ei = S-1R-1TRS, где
S и S-1, — преобразование на коммутационной панели на входе и выходе соответственно;
R и R-1 — преобразование в роторах на входе и выходе;
T — преобразование на рефлекторе.
Опустив коммутационную панель выразим внутреннее преобразование Энигмы через Pi:
Pi = R-1TR
Теперь шифрование можно записать как:
Ei = S-1PiS
Используя формулу перепишем подстановки из примера в 14, 15 и 20 позициях.
S-1P14S(A) = G или что одно и тоже P14S(A) = S(G).
P15S(G) = S(K)
P20S(K) = S(A)
Заменив в последнем выражении S(K) получим:
P20P15P14S(A) = S(A) (1), где S(A) — буква, соединенная с A на коммутационной панели.
Теперь атака сводится к тривиальному перебору всех возможных установок ротора. Для каждой комбинации роторов необходимо проверить выполнение равенства (1). Если равенство выполняется для буквы S, это означает что найдена правильная конфигурация роторов и что буква A соединена на коммутационной панели с буквой S. Поиск остальных пар сводится к по буквенной расшифровке криптотекста и сопоставлению результата с известным открытым текстом.
Следует отметить, что с вероятностью 1/26 равенство может выполняться и при неправильной установке роторов, поэтому для повышения надежности алгоритма желательно использовать несколько «циклов».
Еще один важный момент связан с тем, что атакующему может быть известна только часть зашифрованного сообщения. И в таком случае, прежде всего ему потребуется найти местоположение известного текста в полученной криптограмме. В решении этой задачи очень сильно помогает знание того факта, что Энигма никогда не шифрует букву саму в себя. Т.е. для нахождения правильного смещения нужно найти такую позицию в криптотексте при которой ни одна из букв закрытого текста не дублируется буквой открытого сообщения.
P.S.
Очень медленную, но вполне рабочую реализацию атаки на Python можно посмотреть на GitHub.
Ссылки
