Книга «Совершенный алгоритм. Основы»
Привет, Хаброжители! Эта книга основана на онлайн-курсах по алгоритмам, которые Тим Рафгарден ведет на Coursera и Stanford Lagunita, а появились эти курсы благодаря лекциям для студентов, которые он читает в Стэнфордском университете на протяжении многих лет.
Алгоритмы — это сердце и душа computer science. Без них не обойтись, они есть везде — от сетевой маршрутизации и расчетов по геномике до криптографии и машинного обучения. «Совершенный алгоритм» превратит вас в настоящего профи, который будет ставить задачи и мастерски их решать как в жизни, так и на собеседовании при приеме на работу в любую IT-компанию. Тим Рафгарден расскажет об асимптотическом анализе, нотации большое-О, алгоритмах «разделяй и властвуй», рандомизации, сортировки и отбора. Книга адресована тем, у кого уже есть опыт программирования. Вы перейдете на новый уровень, чтобы увидеть общую картину, разобраться в низкоуровневых концепциях и математических нюансах.
*6.3. Алгоритм DSelect
Алгоритм RSelect выполняется за линейное время для каждого входа, в котором математическое ожидание связано со случайными вариантами выбора, выполняемыми алгоритмом. Требуется ли рандомизация для линейного выбора? В этом разделе и далее эта задача решается при помощи детерминированного линейного алгоритма для задачи выбора.
Для задачи сортировки среднее время работы O (n log n) рандомизированного алгоритма QuickSort совпадает со временем работы детерминированного алгоритма MergeSort, и оба алгоритма — QuickSort и MergeSort — являются полезными алгоритмами для применения на практике. С другой стороны, хотя детерминированный линейный алгоритм выбора, описанный в этом разделе, на практике работает нормально, он не конкурирует с алгоритмом RSelect. Это происходит по двум причинам: из-за больших постоянных множителей во времени работы алгоритма DSelect и выполняемой алгоритмом работы, связанной с выделением и управлением дополнительной оперативной памятью. Тем не менее идеи в алгоритме настолько круты, что я не могу вам о них не рассказать.
6.3.1. Гениальная идея: медиана медиан
Алгоритм RSelect быстр, потому что имеется высокая вероятность того, что случайные опорные элементы будут довольно хорошими, обеспечивая примерно сбалансированное разбиение входного массива после разделения, к тому же довольно хорошие опорные элементы быстро прогрессируют. Если нам не разрешено использовать рандомизацию, то каким образом можно вычислить довольно хороший опорный элемент, не делая слишком много работы?
Гениальная идея в детерминированном линейном выборе заключается в использовании «медианы медиан» в качестве прокси для истинной медианы. Алгоритм рассматривает элементы входного массива как спортивные команды и проводит турнир на выбывание в два тура, чемпионом которого является опорный элемент; см. также рис. 6.1.
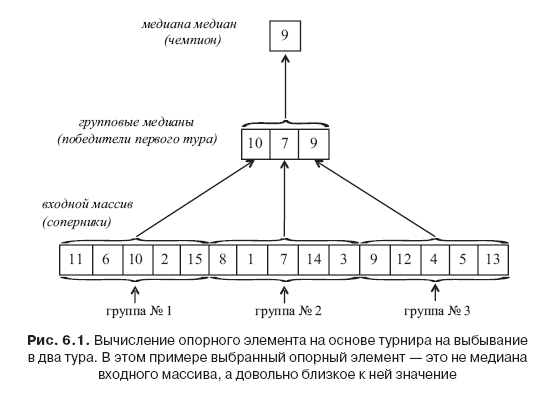
Первый тур является групповым этапом с элементами в позициях 1−5 входного массива в качестве первой группы, элементами в позициях 6−10 в качестве второй группы и так далее. Победитель первого тура группы из пяти элементов определяется как медиана элемента (то есть третий наименьший). Поскольку имеется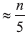 
групп из пяти элементов, есть 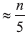первых победителей. (Как обычно, мы игнорируем дроби для простоты.) Чемпион турнира определяется как медиана победителей первого тура.
6.3.2. Псевдокод для алгоритма DSelect
Как на самом деле вычислить медиану медиан? Реализация первого этапа турнира на выбывание проста, поскольку каждое вычисление медианы включает в себя всего пять элементов. Например, каждое такое вычисление может быть выполнено методом перебора (для каждой из пяти возможностей подробно проверить, является ли он срединным элементом) либо с использованием нашего сведения к задаче сортировки (раздел 6.1.2). Для реализации второго этапа мы вычисляем медиану из 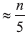победителей первого тура рекурсивно.
Строки 1−2 и 6−13 идентичны алгоритму RSelect. Строки 3−5 являются единственной новой частью алгоритма; они вычисляют медиану медианы входного массива, заменяя строку в алгоритме RSelect, которая выбирает опорный элемент случайным образом.
Строки 3 и 4 вычисляют победителей первого тура турнира на выбывание, где срединный элемент каждой группы из пяти элементов вычисляется с использованием метода перебора или алгоритма сортировки, и копируют этих победителей в новый массив С. Строка 5 вычисляет чемпиона турнира путем рекурсивного вычисления медианы массива С; поскольку C имеет длину (ориентировочно)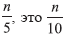 
-я порядковая статистика массива С. На любом шаге алгоритма никакая рандомизация не используется.
6.3.3. Понимание алгоритма DSelect
Рекурсивный вызов алгоритма DSelect при вычислении опорного элемента может показаться опасно цикличным. Чтобы понять, что происходит, давайте сначала обозначим общее количество рекурсивных вызовов.
Правильный ответ: (в). Отбросив базовый случай и счастливый случай, в которых опорный элемент оказывается требуемой порядковой статистикой, алгоритм DSelect делает два рекурсивных вызова. Чтобы понять почему, не перемудрите; просто проверьте псевдокод алгоритма DSelect построчно. В строке 5 имеется один рекурсивный вызов и еще один в строке 11 либо 13.
Есть два вызывающих путаницу распространенных вопроса насчет этих двух рекурсивных вызовов. Во-первых, не является ли тот факт, что алгоритм RSelect делает всего один рекурсивный вызов, причиной, по которой он работает быстрее, чем наши алгоритмы сортировки? Разве алгоритм DSelect не отказывается от этого улучшения, делая два рекурсивных вызова? Раздел 6.4 показывает, что, поскольку дополнительный рекурсивный вызов в строке 5 должен решить только относительно небольшую подзадачу (с 20% элементов исходного массива), мы все еще можем спасти линейный анализ.
Во-вторых, два рекурсивных вызова играют принципиально разные роли. Целью рекурсивного вызова в строке 5 является определение хорошего опорного элемента для текущего рекурсивного вызова. Цель рекурсивного вызова в строке 11 или 13 обычная — рекурсивно решить более мелкую оставшуюся задачу, оставленную текущим рекурсивным вызовом. Тем не менее рекурсивная структура в алгоритме DSelect полностью следует традиции всех других алгоритмов «разделяй и властвуй», которые мы изучали: каждый рекурсивный вызов делает небольшое количество последующих рекурсивных вызовов со строго более мелкими подзадачами и выполняет некоторую дополнительную работу. Если бы мы не беспокоились о том, что алгоритмы, такие как MergeSort или QuickSort, будут выполняться вечно, то нам не следовало бы беспокоиться и об алгоритме DSelect.
6.3.4. Время работы алгоритма DSelect
Алгоритм DSelect — это не просто четко сформулированная программа, которая завершается за ограниченное количество времени, — он выполняется за линейное время, делая больше работы только на постоянный множитель, чем необходимо для чтения входных данных.
Теорема 6.6 (время работы алгоритма DSelect). Для каждого входного массива длиной n ≥ 1 время работы алгоритма DSelect составляет O (n).
В отличие от времени работы алгоритма RSelect, которое в принципе может быть не больше Θ (n2), время работы алгоритма DSelect всегда равняется O (n). Тем не менее на практике вам следует предпочесть RSelect алгоритму DSelect, потому что первый работает на том же месте, а константа, скрытая в среднем времени работы «O (n)» в теореме 6.1, меньше константы, скрытой в теореме 6.6.
» Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок
Для Хаброжителей скидка 20% по купону — Алгоритмы
По факту оплаты бумажной версии книги на e-mail высылается электронная версия книги.
P.S.: 7% от стоимости книги пойдет на перевод новых компьютерных книг, список сданных в типографию книг здесь.
