Книга «Грокаем алгоритмы искусcтвенного интеллекта»
 Привет, Хаброжители!
Привет, Хаброжители!
Искусственный интеллект — часть нашей повседневной жизни. Мы встречаемся с его проявлениями, когда занимаемся шопингом в интернет-магазинах, получаем рекомендации «вам может понравиться этот фильм», узнаем медицинские диагнозы… Чтобы уверенно ориентироваться в новом мире, необходимо понимать алгоритмы, лежащие в основе ИИ.
«Грокаем алгоритмы искусственного интеллекта» объясняет фундаментальные концепции ИИ с помощью иллюстраций и примеров из жизни. Все, что вам понадобится, — это знание алгебры на уровне старших классов школы, и вы с легкостью будете решать задачи, позволяющие обнаружить банковских мошенников, создавать шедевры живописи и управлять движением беспилотных автомобилей.
Книга рассчитана на тех, кто имеет базовое представление о таких понятиях программирования, как переменные, типы данных, массивы, условные конструкции, итераторы, классы и функции; кто имеет опыт разработки на любом языке;, а также тех, кто знаком с основными математическими понятиями: переменной величиной, способами задания функций, отображением функций и данных на графиках.
Отбор родителей на основе их приспособленности
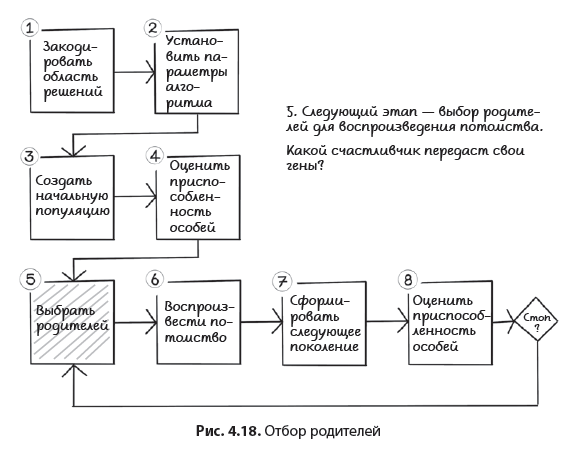
Следующим шагом алгоритма идет отбор родителей для воспроизводства новых особей. В теории Дарвина у наиболее приспособленных особей вероятность воспроизведения больше, потому что живут они, как правило, дольше. Более того, поскольку эти особи лучше приспособлены к окружающей среде, их признаки предпочтительнее для наследования. Тем не менее некоторые особи могут воспроизводить потомство, даже не будучи лидирующими представителями вида, и обладать сильными чертами, не будучи сильными в целом.
Для каждой особи вычисляется ее приспособленность, используемая для определения вероятности выбора этой особи в качестве родителя. Это свойство делает генетический алгоритм стохастическим по своей природе (рис. 4.18).
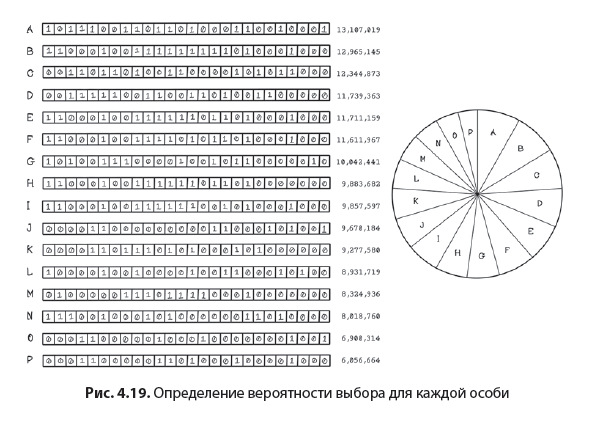
Часто в качестве инструмента для отбора родителей на основе их приспособленности используют колесо рулетки. В этом подходе особям на основе степени их приспособленности выделяется определенная доля колеса. То есть чем выше приспособленность, тем большую секцию поля занимает особь, и шанс ее выбора возрастает. После этого колесо «вращается» и выбирается победитель. Этот процесс повторяется, пока не будет отобрано нужное количество родителей.
Колесо вычисляет вероятности для 16 особей с различной степенью приспособленности и выделяет секцию для каждой особи. Поскольку у многих особей приспособленность похожа, для них выделяются секции примерно одинакового размера (рис. 4.19).
Количество отобранных родителей определяется согласно общему требуемому количеству потомков, которое, в свою очередь, обусловливается требуемым размером популяции для каждого поколения. Выбираются два родителя, и создается потомок. Этот процесс повторяется для разных выбранных родителей (с возможностью повторного участия особей в воспроизводстве потомства) до момента достижения нужного числа потомков. Двое родителей могут воспроизвести одного или двух смешанных потомков. Этот принцип будет пояснен подробнее несколько позже. В примере задачи о рюкзаке особи с большей степенью приспособленности — это такие, которые заполняют рюкзак с наибольшей общей ценностью, не превышая ограничения по весу.
Для контроля разнообразия популяции используются различные подходы, в частности стратегия стационарного состояния и «поколенческая» стратегия, каждая из которых имеет свои преимущества и недостатки.
Стационарное состояние: смена в каждом новом поколении только части популяции
Этот высокоуровневый подход управления популяцией не заменяет другие стратегии отбора, а служит схемой их использования. Его идея состоит в сохранении большей части популяции и замене новым потомством только небольшой группы наиболее слабых особей. Этот процесс подобен циклам жизни и смерти, в которых более слабые особи умирают и на их смену вследствие размножения приходят новые. Если популяция состоит из 100 особей, то в следующем поколении, например, 80 из них продолжат существовать, а 20 будут замещены потомством.
Поколенческая модель: полная смена популяции каждое поколение
Этот высокоуровневый подход к управлению популяцией аналогичен предыдущему и не заменяет другие стратегии отбора. В поколенческой модели создается столько же потомков, сколько особей есть в текущей популяции, и популяция полностью ими заменяется. Если популяция состоит из 100 особей, то каждое поколение будет производить 100 потомков. Стратегия стационарного состояния и поколенческая стратегия — ключевые принципы построения конфигурации алгоритма.
Согласно такому же принципу хромосомы приравниваются к секциям колеса. Чем выше приспособленность хромосомы, тем больше окажется размер ее секции. Далее по аналогии с шариком в рулетке случайным образом выбирается выигравшая хромосома.
Эта аналогия — пример вероятностного отбора. У каждой особи есть шанс пройти отбор. В результате от этого шанса зависит конечное разнообразие популяции и скорость ее конвергенции, о которой мы говорили ранее в этой главе. Рисунок 4.19 выше также демонстрирует данный принцип.
Псевдокод
Сначала нужно определить вероятность выбора каждой особи. Эта вероятность вычисляется путем деления показателя приспособленности особи на общую приспособленность популяции. Далее можно использовать отбор рулеткой.
Колесо вращается столько раз, сколько требуется выбрать особей. Для каждого отбора вычисляется случайное десятичное число между 0 и 1. Если приспособленность особи оказывается в рамках этой вероятности, особь отбирается. Для определения вероятности отбора особи можно использовать и другие подходы, включая стандартное отклонение, в котором значение особи сравнивается со средним значением группы:
Колесо рулетки: отбор родителей и выживших особей
У хромосом с более высоким показателем приспособленности больше шансов быть выбранными, но это не мешает хромосомам с низким показателем также пройти отбор. Выражение отбор колесом рулетки взято из индустрии казино, где игровое поле рулетки разделено на секции. В начале игры колесо раскручивают, после чего в него вбрасывается шарик. По завершении вращения выигрывает секция, где в итоге остановился шарик.

Отбор родителей на основе их приспособленности
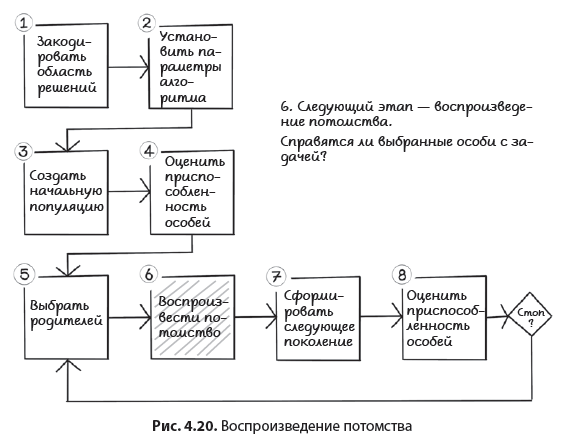
После отбора родителей наступает этап воспроизведения ими нового потомства. Как правило, этот процесс состоит из двух шагов. Первый — это кроссинговер (кроссовер), то есть смешивание части хромосомы одного родителя с частью хромосомы другого и наоборот. В результате этого процесса получаются два потомка, которые содержат инверсионную смесь генов родителей. Второй шаг — это мутация, подразумевающая небольшое случайное изменение потомка для увеличения разнообразия популяции (рис. 4.20).
Кроссинговер
Кроссинговер — это процесс смешения генов двух особей для создания одного или более потомков. В основе этого процесса лежит принцип размножения. Потомки являются частью своих родителей, в зависимости от используемой стратегии кроссинговера, которая, в свою очередь, сильно зависит от стратегии кодирования.
Одноточечный кроссинговер: наследование одной части от каждого родителя
В этом случае выбирается одна точка в структуре хромосомы. Далее происходит обращение к обоим родителям, и от первого из них берется первая часть, а от второго вторая. В результате совмещения этих частей получается потомок. Второй потомок может получиться путем использования второй части первого родителя и первой части второго, то есть инверсионным способом.
Одноточечный кроссинговер применим к двоичному кодированию, пермутационному/порядковому или вещественному (рис. 4.21). Эти схемы кодирования будут рассматриваться в главе 5.

Псевдокод
При воспроизведении двух потомков создается пустой массив, в котором они будут храниться. Все гены от индекса 0 до нужного индекса родителя А объединяются со всеми генами от нужного индекса до конца хромосомы родителя B, создавая одного потомка. Второй потомок создается инверсионным порядком объединения частей генов родителей:

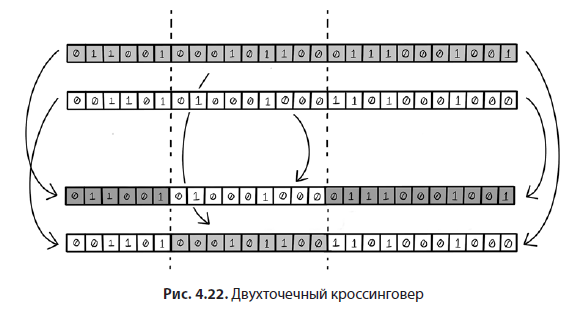
Двухточечный кроссинговер: наследование двух частей от каждого родителя
Выбираются две точки в структуре хромосомы. Далее через поочередное обращение к родителям выбираются их части генов, из которых и составляется потомок. Этот процесс аналогичен рассмотренному выше одноточечному кроссинговеру. Если описать его подробно, то потомок составляется из первой части первого родителя, второй части второго и третьей части первого. Можно представить двухточечный кроссинговер как разделение массивов с целью создания из их частей новых массивов. Этот вид кроссинговера применим к двоичному и вещественному кодированию (рис. 4.22).
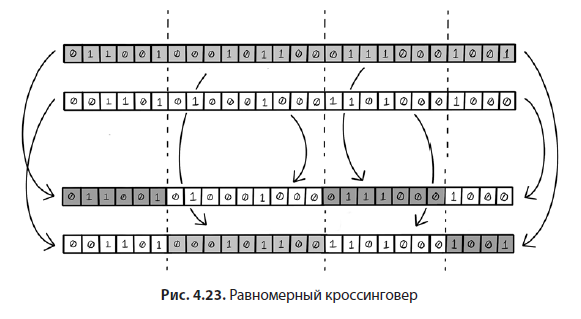
Однородный кроссинговер: наследование множества частей от обоих родителей
Однородный кроссинговер — это усовершенствованный двухточечный кроссинговер. Он подразумевает создание маски, представляющей, какие гены от каждого родителя будут использованы для генерации потомка. Для создания второго потомка может применяться инверсионный процесс. Чтобы добиться максимального разнообразия, маску можно генерировать случайным образом при создании каждого потомка. Говоря в общем, в результате однородного кроссинговера рождаются более разнообразные особи, потому что признаки потомка сильно отличаются от любого из родителей. Данный кроссинговер применим к двоичному и вещественному кодированию (рис. 4.23).
Мутация
Мутация подразумевает небольшое изменение потомков с целью разнообразия популяции. В зависимости от задачи и метода кодирования могут использоваться различные способы мутации.
Одним из параметров мутации является ее частота — вероятность, что хромосома потомка будет изменена. По аналогии с живыми организмами некоторые хромосомы изменяются больше других. В результате генотип потомка является не точной комбинацией хромосом родителей, а содержит небольшие отличия. Мутация важна для обеспечения разнообразия в популяции и предотвращения застревания алгоритма в локальных лучших решениях.
Высокая частота мутаций означает либо высокую вероятность выбора особи для мутации, либо высокую вероятность мутации генов в хромосоме особи, что будет зависеть от выбранной стратегии мутирования. Высокий показатель мутации предполагает большее разнообразие, но нужно учитывать, что чрезмерное разнообразие может привести к отклонению от хороших решений.
Ришал страстно увлечен бизнес-механиками и стратегиями, развитием людей и команд, а также искусственным интеллектом и философией. Он создал немало различных цифровых продуктов для повышения эффективности работы, чтобы люди и компании могли сосредоточиться на наиболее важных вещах. Помимо этого, он неоднократно выступал на международных конференциях, объясняя сложные понятия доступным языком и помогая людям совершенствовать знания и навыки.
Более подробно с книгой можно ознакомиться на сайте издательства:
» Оглавление
» Отрывок
По факту оплаты бумажной версии книги на e-mail высылается электронная книга.
Для Хаброжителей скидка 25% по купону — Алгоритмы
